NCERT Solutions for Class 11 Physics Chapter 9 Mechanical Properties Of Fluids

Q 9.1 (a) Explain why

The blood pressure in humans is greater at the feet than at the brain

Answer:

The pressure in a fluid column increases with the height of the column. As the height of the blood column is more than that of the brain, the blood pressure in the feet is more than the blood pressure in the brain.

Q 9.1 (b) Explain why

Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km

Answer:

This is because the air density does not remain the same in the atmosphere. It decreases exponentially as height increases.

Q 9.1 (c) Explain why

Hydrostatic pressure is a scalar quantity, even though pressure is force divided by area.

Answer:

When a force is applied on a fluid, the pressure which gets generated is uniformly transmitted to all directions and therefore has no particular direction and is a scalar quantity. We talk of the division of force with area only while considering the magnitudes. The actual vector form of the relation is $\vec{F}=p\vec{A}$

Q 9.2 (a) Explain why

(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute.

Answer:

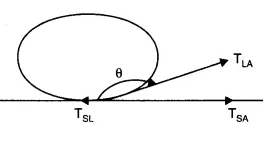
$T_{SL}$ = Surface tension corresponding to the solid-liquid layer

$T_{LA}$ = Surface tension corresponding to liquid-air layer

$T_{SA}$ = Surface tension corresponding to solid-air layer

The angle of contact is $\theta$

Since the liquid is not flowing over the solid surface, the components of $T_{SL}$, $T_{LA}$ and $T_{SA}$ along the solid surface must cancel out each other.

$T_{SL}+T_{LA}cos\theta =T_{SA}$
$ cos\theta =\frac{T_{SA}-T_{SL}}{T_{LA}}$

In case of mercury, $T_{SA}$ < $T_{SL}$ and therefore $cos\theta <0$ and therefore $\theta >\frac{\pi }{2}$, i.e the angle of contact of mercury with glass is obtuse.

Q 9.2 (b) Explain why

(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)

Answer:

Cohesive forces between water molecules are much less than adhesive forces between water and glass molecules, and that's why water tends to spread out on glass, whereas cohesive forces within mercury are comparable to adhesive forces between mercury and glass, and that's why mercury tends to form drops.

Q 9.2 (c) Explain why

(c) Surface tension of a liquid is independent of the area of the surface

Answer:

Surface tension is the force acting per unit length at the interface of a liquid and another surface. Since this force itself is independent of area, the surface tension is also independent of area.

Q 9.2 (d) Explain why

(d) Water with detergent dissolved in it should have small angles of contact.

Answer:

As we know, a detergent with water rises very fast in the capillaries of clothes, which is only possible when the cosine of the angle of contact is large, i.e. angle of contact must be small.

Q 9.2 (e) Explain why

(e) A drop of liquid under no external forces is always spherical in shape

Answer:

While in a spherical shape, the surface area of the drop of liquid will be minimum, and thus the surface energy would be minimum. A system always tends to be in a state of minimum energy, and that's why, in the absence of external force, a drop of liquid is always spherical in shape.

Q 9.3 Fill in the blanks using the word(s) from the list appended with each statement:

(a) Surface tension of liquids generally ... with temperatures (increases/decreases)

(b) Viscosity of gases ... with temperature, whereas viscosity of liquids ... with temperature (increases/decreases)

(c) For solids with elastic modulus of rigidity, the shearing force is proportional to ..., while for fluids it is proportional to ... (shear strain/rate of shear strain)

(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli’s principle)

(e) For the model of a plane in a wind tunnel, turbulence occurs at a ... speed for turbulence for an actual plane (greater / smaller)

Answer:

(a) The surface tension of liquids generally decreases with temperature.

(b) The viscosity of gases increases with temperature, whereas the viscosity of liquids decreases with temperature.

(c) For solids with elastic modulus of rigidity, the shearing force is proportional to shear strain, while for fluids it is proportional to the rate of shear strain.

(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows from conservation of mass, while the decrease in pressure there follows from Bernoulli’s principle.

(e) For the model of a plane in a wind tunnel, turbulence occurs at a greater speed for turbulence for an actual plane.

Q 9.4 (a) Explain why

(a) To keep a piece of paper horizontal, you should blow over, not under, it

Answer:

As per Bernoulli's principle, when we blow over a piece of paper, the pressure there decreases while the pressure under the piece of paper remains the same, and that's why it remains horizontal.

Q 9.4 (b) Explain why

(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers

Answer:

This is because when we cover the tap, there are very small gaps remaining for the water to escape, and it comes out at very high velocity in accordance with the equation of continuity.

Q 9.4 (c) Explain why

(c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection

Answer:

Because of the extremely small size of the opening of a needle, its size can control the flow with more precision than the thumb of a doctor.

According to the equation of continuity, area * velocity = constant. If the area is very small, the velocity must be large. Thus, if the area is small flow becomes smooth

Q 9.4 (d) Explain why

(d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel

Answer:

Through a small area, the velocity will be large. A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel in accordance with the law of conservation of linear momentum.

Q 9.4 (e) Explain why

(e) A spinning cricket ball in the air does not follow a parabolic trajectory

Answer:

The ball, while travelling, rotates about its axis as well, causing a difference in air velocities at different points around it, thus creating a pressure difference which results in external forces. In the absence of air, a ball would have travelled along the expected parabolic path.

Q 9.5 A 50 kg girl wearing high-heeled shoes balances on a single heel. The heel is circular with a diameter of 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?

Answer:

Mass of the girl m = 50 kg.

Gravitational acceleration g = 9.8 m s -2

Weight of the girl (W), mg = 490 N

$\\Pressure=\frac{Force}{Area}\\ =\frac{490}{\pi \left ( \frac{1\times 10^{-2}}{2} \right )^{2}}\\ =6.24\times 10^{6}Pa$

Q 9.6 Torricelli's barometer used mercury. Pascal duplicated it using French wine of density 984 kg $m^{-3}$. Determine the height of the wine column for normal atmospheric pressure.

Answer:

Atmospheric pressure is $P=1.01\times 10^{5}Pa$

The density of French wine $\rho_{w}= 984\ kg\ m^{-3}$

Height of the wine column h w would be

$h_{w}=\frac{P}{\rho _{w}g}$
$h_{w}=\frac{1.01\times 10^{5}}{984\times 9.8}$
$h_{w}=10.474m$

Q 9.7 A vertical offshore structure is built to withstand a maximum stress of $10^{9}$ Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.

Answer:

The density of water is $\rho _{w}=1000\ kg\ m^{-3}$

The depth of the ocean is 3 km

The pressure at the bottom of the ocean would be

$P=\rho _{w}gh$
$ P=1000\times 9.8\times 3\times 1000 $
$ P=2.94\times 10^{7}Pa$

The above value is much less than the maximum stress the structure can withstand, and therefore, it is suitable for putting up on top of an oil well in the ocean.

Q 9.8 A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 $cm^{2}$. What maximum pressure would the smaller piston have to bear?

Answer:

Maximum Pressure that the piston would have to bear is

$\\P_{max}=\frac{Maximum\ weight\ of\ a\ car}{Area\ of\ the\ piston}\\ =\frac{3000\times 9.8}{425\times 10^{-4}}\\ =6.917\times 10^{5} Pa$

Q 9.9 A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit?

Answer:

Since the mercury columns in the two arms are equal, the pressure exerted by the water and the spirit column must be the same.

$\\h_{w}\rho _{w}g=h_{s}\rho _{s}g$
$ \frac{\rho _{s}}{\rho _{w}}=\frac{h_{w}}{h_{s}}$
$ \frac{\rho _{s}}{\rho _{w}}=\frac{10}{12.5}\\ $
$\frac{\rho _{s}}{\rho _{w}}=0.8$

Therefore, the specific gravity of spirit is 0.8.

Q 9.10 In the previous problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = 13.6)

Answer:

Let the difference in the levels of mercury in the two arms be hHg

$\begin{aligned}
& \left(\rho_w-\rho_s\right) g h=\rho_{H g} g h_{H g} \\
& \left(1-\frac{\rho_s}{\rho_w}\right) h=\frac{\rho_{H g}}{\rho_w} h_{H g} \\
& (1-0.8) \times 15=13.68 h_{H g} \\
& h_{H g}=\frac{0.2 \times 15}{13.6} \\
& h_{H g}=0.22 \mathrm{~cm}
\end{aligned}$

Q 9.11 Can Bernoulli’s equation be used to describe the flow of water through a rapid in a river? Explain.

Answer:

No. Bernoulli's equation can be used only to describe streamline flow, and the flow of water in a river is turbulent.

Q 9.12 Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain

Answer:

No, unless the atmospheric pressures at the two points where Bernoulli’s equation is applied are significantly different.

Q 9.13 Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end is 4.0 × $10^{-3}$ kg $s^{-1}$, what is the pressure difference between the two ends of the tube? (Density of glycerine = 1.3 × $10^{3}$ kg $m^{-3}$ and viscosity of glycerine = 0.83 Pa s). [You may also like to check if the assumption of laminar flow in the tube is correct].

Answer:

The volumetric flow rate of glycerine would be given by

$V=\frac{Amount\ of\ glycerine\ flow\ per\ second\ }{Density\ of\ glycerine}$
$ V=\frac{M}{\rho }$
$ V=\frac{4\times 10^{-3}}{1.3\times 10^{3}}$
$ V=3.08\times 10^{-6}ms^{-1}$

The viscosity of glycerine is $\eta =0.83\ Pa\ s$

Assuming Laminar flow for a tube of radius r, length l, having a pressure difference P across its ends, a fluid with viscosity $\eta$ would flow through it with a volumetric rate of

$\\V=\frac{\pi Pr^{4}}{8\eta l}$
$ P=\frac{8V\eta l}{\pi r^{4}}$
$P=\frac{8\times 3.08\times 10^{-6}\times 0.83}{\pi \times (10^{-2})^{4}}$
$ P=9.75\times 10^{2}\ Pa$

Reynolds' number is given by

$R=\frac{4\rho V}{\pi d\eta }$
$ R=\frac{2\rho V}{\pi r\eta }$
$ R=\frac{2\times 1.3\times 10^{3}\times 3.08\times 10^{-6}}{\pi \times 0.01\times 0.83}\\ R\approx 0.3$

Since the Reynolds Number is coming out to be 0.3, our assumption of laminar flow was correct.

Q 9.14 In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m $s^{-1}$ and 63 $ms^{-1}$ respectively. What is the lift on the wing if its area is 2.5 $m^{2}$? Take the density of air to be 1.3 kg $m^{-3}$

Answer:

The speeds of air above and below the wings are given to be $v_{1}$ = 70 m $s^{-1}$ and $v_{2}$ = 63 m $s^{-1},$ respectively.

Let the pressure above and below the wings be $P_{1}$ and $P_{2}$, and let the model aeroplane be flying at a height h from the ground.

Applying Bernoulli's Principle on two points above and below the wings, we get

$\begin{aligned}
& P_1+\rho g h+\frac{1}{2} \rho v_1^2=P_2+\rho g h+\frac{1}{2} \rho v_2^2 \\
& P_2-P_1=\frac{1}{2} \rho\left(v_1^2-v_2^2\right) \\
& \Delta P=\frac{1}{2} \times 1.3 \times\left(70^2-63^2\right) \\
& \Delta P=605.15 \mathrm{~Pa}
\end{aligned}$

The pressure difference between the regions below and above the wing is 605.15 Pa

The lift on the wing is F

$\begin{aligned}
& F=\Delta P \times \text { Area of wing } \\
& F=605.15 \times 2.5 \\
& F=1512.875 \mathrm{~N}
\end{aligned}$

Q 9.16 The cylindrical tube of a spray pump has a cross-section of 8.0 $cm^{2}$ one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m $min^{-1}$, what is the speed of ejection of the liquid through the holes?

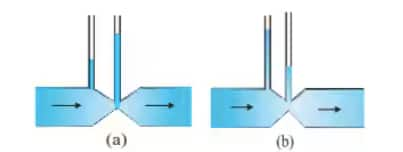
Answer:

Cross-sectional area of cylindrical tube is $\mathrm{a}_1=8.0 \mathrm{~cm}^2$
The total area of the 40 fine holes is $a_2$

$\begin{aligned}
& a_2=40 \pi\left(\frac{d^2}{4}\right) \\
& a_2=40 \times \pi \times \frac{\left(10^{-3}\right)^2}{4} \\
& a_2=3.143 \times 10^{-5} \mathrm{~m}^2
\end{aligned}
$

Speed of liquid inside the tube is $\mathrm{v}_1=1.5 \mathrm{~m} \mathrm{~min}^{-1}$
Let the speed of ejection of fluid through the holes be $\mathrm{v}_2$
Using the continuity equation

$\begin{aligned}
& a_1 v_1=a_2 v_2 \\
& v_2=\frac{a_1 v_1}{a_2} \\
& v_2=\frac{8 \times 10^{-4} \times 1.5}{60 \times 3.143 \times 10^{-5}} \\
& v_2=0.636 \mathrm{~m} \mathrm{~s}^{-1}
\end{aligned}$

Q 9.17 A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × $10^{-2}$ N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?

Answer:

Total weight supported by the film $W=1.5 \times 10^{-2} N$
Since a soap film has two surfaces, the total length of the liquid film is 60 cm.
Surface Tension is T

$\begin{aligned}
T & =\frac{W}{l} \\
T & =\frac{1.5 \times 10^{-2}}{60 \times 10^{-2}} \\
T & =2.5 \times 10^{-2} \mathrm{Nm}^{-1}
\end{aligned}$

Q 9.19 What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature? Surface tension of mercury at that temperature (20 °C) is 4.65 × $10^{-1}$ N $m^{-1}$ . The atmospheric pressure is 1.01 × $10^{5}$ Pa. Also, give the excess pressure inside the drop.

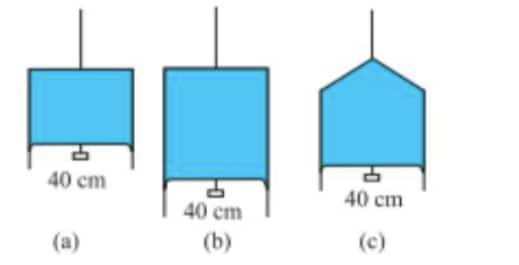
Answer:

Surface Tension of Mercury is $T=4.65 \times 10^{-1} \mathrm{~N} \mathrm{~m}^{-1}$
The radius of the drop of Mercury is $r=3.00 \mathrm{~mm}$
Excess pressure inside the Mercury drop is given by

$\begin{aligned}
& \Delta P=\frac{2 T}{r} \\
& \Delta P=\frac{2 \times 4.65 \times 10^{-1}}{3 \times 10^{-3}} \\
& \Delta P=310 \mathrm{~Pa}
\end{aligned}$

Atmospheric Pressure is $P_0=1.01 \times 10^5 \mathrm{~Pa}$
Total Pressure inside the Mercury drop is given by

$\begin{aligned}
& P_T=\Delta P+P_0 \\
& P_T=310+1.01 \times 10^5 \\
& P_T=1.0131 \times 10^5
\end{aligned}$