NCERT Class 11 Physics Chapter 10 Notes Mechanical Properties of Fluids - Download PDF
Have you ever wondered why rivers can flow, aeroplanes can fly freely in the air, or bubbles can appear in the water? All these interesting phenomena are described in Chapter 9 of Physics 11 - Mechanical Development of Fluids. This chapter discusses the motion of liquids and gases when subjected to forces, which becomes an essential section in CBSE, JEE and NEET preparations. The NCERT Notes for Class 11 Physics Chapter 9 Mechanical Properties of Fluids have been carefully prepared by Careers360 subject experts following the latest CBSE syllabus to make complex topics easy to grasp.
This Story also Contains
- Class 11 Physics Chapter 9 Mechanical Properties of Fluids Notes: Download PDF
- NCERT Notes for Class 11 Physics Chapter 9
- Class 11 Physics Chapter 9 Mechanical Properties of Fluids: Previous Year Questions and Answers
- How to Master Class 11 Physics Chapter 9 Mechanical Properties of Fluids?
- Importance of Mechanical Properties of Fluids Class 11 Notes
- NCERT Class 12 Notes Chapter-Wise
- NCERT Books and Syllabus

The NCERT Notes for Class 11 Physics Chapter 9 Mechanical Properties of Fluids introduce most of the essential concepts like the variation of pressure with depth, the principle of Bernoulli, and buoyancy, as well as the flow of fluids under various circumstances. These NCERT notes are thorough and contain many examples of the real world, clear explanations, well-labelled diagrams, and important formulas and are equipped to offer a complete and student-friendly study tool. The PDF can be easily downloaded at no cost, and the students can revise and reinforce their knowledge to achieve good grades in the CBSE board and competitive exams.
Also Read
Class 11 Physics Chapter 9 Mechanical Properties of Fluids Notes: Download PDF
The Class 11 Physics Chapter 9 Mechanical Properties of Fluids Notes are readily available in PDF format, and the students can readily access and download them to revise in a quick and effective manner. The Class 11 Physics Chapter 9 Mechanical Properties of Fluids Notes are written by highly qualified faculty members as per the recent CBSE syllabus, and they comprise all the main concepts, formulae, and derivations in simple, easy-to-understand form. In these brief notes, students are in a position to reinforce their knowledge on fundamental concepts, prepare effectively for board exams of the CBSE, and develop a solid base for the JEE and NEET.
NCERT Notes for Class 11 Physics Chapter 9
The Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE notes assist students to gain a clear picture regarding the behaviour of liquids and gases when exposed to various conditions of force and pressure. These Mechanical Properties of Fluids Class 11 Physics notes do not complicate complex concepts such as buoyancy, viscosity and the Bernoulli theorems by means of easy explanations and examples. They are made according to the new NCERT curriculum and are a great source of revision and exam preparation in a short period of time for both CBSE and competitive exams, such as JEE and NEET.
What are Fluids?
-
Fluids are substances that can flow when an external force is applied to them.
-
Gases and Liquids are fluids.
-
It does not have a finite shape; rather, it takes the shape of the vessel that contains it.
-
The normal force exerted by the liquid when it is at rest on a surface is called the thrust of the liquid.
-
SI unit of thrust = (N) Newton.
-
Fluid mechanics is divided as follows
-
When the fluid is at rest - hydrostatics
-
When the fluid is in motion – hydrodynamics
Pressure
-
The normal force applied by a liquid per unit area of the surface in contact is called the pressure of the liquid, also known as Hydrostatic pressure.
-
Pressure applied by a liquid column, p = hρg
Here, h = height of the liquid column,
ρ= density of liquid
g =acceleration because of gravity
Mean pressure on the walls of the container containing liquid up to height h = (hρg / 2).
Density
The density of any material is defined as its mass per unit volume. If a fluid of mass m occupies a volume V, then its density is given as
Density =m/V
Density is usually denoted by the symbol ρ. It is a positive scalar quantity. Its SI unit is $kgm^{−3}$ and its dimensions are [$ML^{−3}$].
Relative Density or Specific Gravity:
The relative density of a substance is defined as the ratio of the density of the substance to the density of water at 4°C. The density of water at 4°C is 1.0×$10^{3}$ kg $m^{−3}$. Relative density is a unitless and dimensionless scalar quantity. It is always positive.
If the density of silver is $10.8×10^{3}$ $kg m^{−3}$, then its relative density is 10.8 .
Density plays an important role in describing the pressure exerted by fluids.
Pascal’s Law
-
According to Pascal’s law at equilibrium, the pressure at any point enclosed in a container is transmitted equally in all directions and on the Walls of the container.
-
The working principle of hydraulic lifts, hydraulic presses, and hydraulic brakes is based on Pascal’s law.
-
Atmospheric Pressure
-
The pressure that is exerted by the atmosphere on Earth is known as atmospheric pressure.
-
It is almost 100000 N/m2.
-
At sea level, atmospheric pressure becomes equal to 76 cm of mercury column.
-
Atmospheric pressure is given as "hdg", which is equal to that of 76 x 13.6 x 980 dyne cm-2
-
Atmospheric pressure can be measured in a torr or bar. 1 torr = 1 mm of mercury column. 1 bar = 105 Pa
-
The aneroid barometer is the instrument that is used to measure atmospheric pressure.
Variation of Pressure with Depth
As we go deeper into a fluid (like water), the pressure increases. This happens because the weight of the fluid above adds to the pressure below. The pressure at a certain depth in a liquid is given by the formula:
P=h⋅ρ⋅g
Where:
- P is the pressure,
- h is the depth,
- ρ (rho) is the density of the liquid,
- g is the acceleration due to gravity.
So, the deeper you go, the higher the pressure becomes. This is why deep-sea divers need special suits to withstand the increased pressure underwater.
Atmospheric Pressure and Gauge Pressure
Atmospheric Pressure is the pressure exerted by the weight of the air in the Earth's atmosphere. At sea level, it is approximately $1.013×10^{5}$ Pa (Pascal) or 1 atmosphere (atm). This pressure is all around us, but we usually don't feel it because it is balanced by the pressure inside our bodies.
Gauge Pressure is the pressure measured relative to atmospheric pressure. It tells us how much more or less pressure is present in a system compared to the surrounding air pressure. It is given by:
Gauge Pressure = Absolute Pressure - Atmospheric Pressure
Hydraulic Machines
When an external pressure is applied to a confined liquid at rest, it is transferred undiminished to all parts of the liquid, and also to the walls of the vessel containing the liquid. This is Pascal's law for the transmission of fluid pressure.
Let's understand this with the following illustration. Take a vessel having four openings, A, B, C and D as shown. These openings are provided with frictionless, weightless and water-tight pistons.
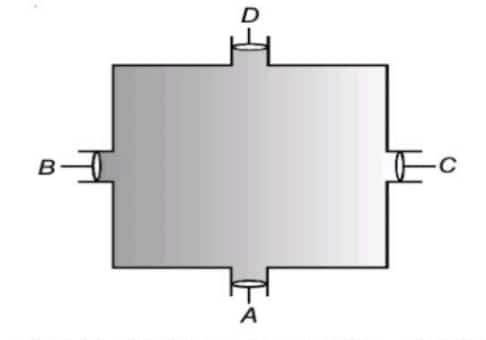
All four openings are equally wide, having a cross-section of a (say). When the piston at A is pushed in with a force F, it exerts a pressure P=F/a on the enclosed fluid. It is found that we require the same force F on each piston B, C and D to keep them from moving. Thus, the pressure at each piston increases by F/a. It proves that external pressure applied to the enclosed fluid is transferred to all points undiminished. This law has many applications in daily life.
Streamline Flow
Till now, we have studied the fluids at rest.
The study of fluids in motion is called fluid dynamics.
When a fluid is in flow, its motion can either be smooth or irregular, depending on its velocity of flow.
When a liquid flows such that each particle of the liquid passing a given point moves along the same path and has the same velocity as its predecessor had at that point, the flow is called streamlined or steady flow.
The path followed by a fluid particle in steady flow is called a streamline.
Properties of Streamlines
(i) The tangent at any point of a streamline gives the direction of flow of a fluid particle at that point.
(ii) In a steady flow, no two streamlines can cross each other, for if they do so, two tangents can be drawn at the point of intersection. It means the incoming fluid particle can go either way or the other. Thus, the flow would not be steady.
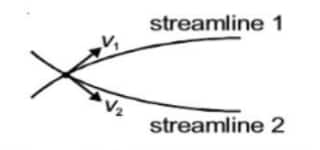
(iii) Fluid velocity remains constant at any point of a streamline, but it may be different at different points of the same streamline.
(iv) Fluid velocity is greater in the regions where streamlines are closely spaced. This can be proved from the equation of continuity that we discuss in the upcoming section.
Equation of Continuity
Consider again a fluid in steady flow. The map of its flow for a particular section can be shown by a bundle of streamlines, as shown below. Here area of cross-section is greater at point Q than that at point P. Hence, streamlines are closely spaced at P than those at Q. Let the area of cross-section and fluid velocity at point P be AP and vP, respectively. Let the corresponding quantities at point Q be AQ and vQ.
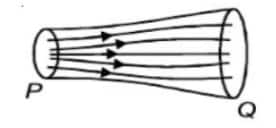
Therefore, the volume of fluid moving in at P, in a small time interval Δt =APvPΔt
Similarly, the volume flowing out at Q, during the same interval Δt,
=AQvQΔt
By conservation of mass, for Δt
mass flowing in at P = mass flowing out at Q.
By conservation of mass, for Δt
mass flowing in at P = mass flowing out at Q.
⇒(APvPΔt)ρP=(AQvQΔt)ρQ [ρP= fluid density at P, ρQ= fluid density at Q]
For the flow of incompressible fluids
ρP=ρQ⇒APvP=AQvQ
This expression is known as the equation of continuity. It is a statement of conservation of mass in the flow of incompressible fluids.
Bernoulli's Principle
Bernoulli's Principle states that for a streamlined flow of an ideal (non-viscous and incompressible) fluid, the total mechanical energy of the fluid remains constant. This total energy includes the pressure energy, kinetic energy, and potential energy per unit volume.
$P+\frac{1}{2} \rho v^2+\rho g h=$ constant
Applications of Bernoulli's Principle:
- Lift in aeroplane wings
- Flow of blood in arteries
- Functioning of a carburettor or atomiser
Limitations of Bernoulli's Equation
1. The equation is valid only for incompressible fluids having streamline flow. It is because it does not take into account the elastic energy of the fluids.
2. It is assumed that no energy is dissipated due to the frictional force exerted by different layers of fluid on each other.
3. It does not hold for non-steady flow. In such a situation, velocity and pressure constantly fluctuate with time.
Speed of Efflux: Torricelli's Law
Torricelli's Law gives the speed of a fluid flowing out of an orifice (small hole) in a tank under the force of gravity. It is based on Bernoulli's Principle and assumes an ideal fluid and streamline flow.
According to Torricelli's Law, the speed of efflux (i.e., the speed at which the liquid leaves the hole) is given by:
$v=\sqrt{2gh}$
Where:
- v = speed of efflux
- g= acceleration due to gravity
- h= height of the fluid column above the hole
Dynamic Lift
Dynamic lift is the upward force experienced by an object when it moves through a fluid (like air or water). This force is generated due to the difference in pressure on different parts of the object caused by its shape and motion.
Viscosity
When a fluid moves, it flows in the form of parallel layers. These layers exert a force on each other which tends to oppose their relative motion. This is similar to what a frictional force does when two solids in contact move or tend to move over each other.
The property of fluid which gives rise to such a frictional force in them is called viscosity.
The force arises when there is relative motion between the layers of a fluid.
-
Viscos Force (F)= -η A(dv/dx)
η =-F/A(dv/dx)
here,
(dv/dx) = rate of change of the velocity with distance and velocity gradient, A = area of cross-section and coefficient of viscosity. -
SI unit of η = Nsm-2 or pascal-second or decapoise.
-
Dimensional formula = [ML-1T-1].
-
The coefficient of viscosity of different oils and their variation with temperature helps us in selecting an appropriate lubricant for a given machine. Viscosity occurs due to the transmission of momentum. The value of viscosity for an ideal liquid is zero. In some organic liquids, it is used in determining the molecular weight and shape of large organic molecules like proteins and cellulose.
Stoke’s Law
Stoke’s Law says that when a small spherical body drops in a liquid column, it sometimes reaches a constant velocity. This velocity is called terminal velocity. When a small spherical object drops in the liquid column with terminal velocity, then the viscous force acting on it is given by
F = 6πηrv
where, r = radius of the body, V = terminal velocity, and η = coefficient of viscosity.
This is called Stokes' law, where,
∙ ρ = density of the body
∙ σ = density of the liquid,
∙ η = coefficient of viscosity of liquid and,
∙ g = acceleration due to gravity
- If ρ > ρ0, the body falls downwards.
- If ρ < p0, the body moves upwards with constant velocity.
- If p0 << ρ, then v = (2r2 ρg/9η)
Importance of Stokes Law
1. It helps to find the electric charge by Millikan’s oil drop experiment.
2. It helps during parachuting..
3. This is the phenomenon behind the formation of clouds.
Surface Tension
-
The property of the liquid by virtue of which the free surface of the liquid starts to minimise due to the force of attraction between the layers of the liquid at rest.
-
The surface tension is the physical property of a liquid in which molecules of the liquid draw each and every surface.
-
SI unit of surface tension = Nm-1
-
Dimensional formula = [MT-2]
Surface Energy
The liquid does not have any shape, and when placed in any container possesses some additional energy, and this energy is different from the molecules that are present in the bulk amount inside the liquid. This energy is present at the surface of the molecules.
The product of surface tension and change in surface area is termed a change in surface energy, and all are under constant temperature conditions.
Surface Energy and Surface Tension
Surface tension is defined as the surface energy per unit area or the force per unit length acting in the plane of the interface between the plane of the liquid and any other substance.
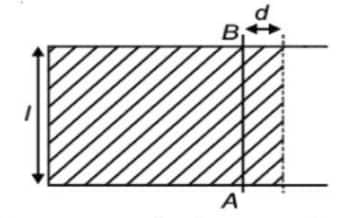
Consider a thin soap film obtained in a rectangular frame as shown above. Let the end AB be free to slide along the horizontal part of the frame. As AB slides to the right by a distance d, some extra work is to be done to increase the surface area and hence the surface energy of the film. Let F be the force required to push AB towards the right. The work done on the film is:
W=Fd
This work done is stored in the film as the extra surface energy. Let the surface tension, i.e., the surface energy per unit area for the given case, be S. Then
S(2dl)=Fd⇒S=F/2l
[Soap film has two free surfaces]
This expression gives the measure of surface tension. The Sl unit of surface tension is $Nm^{−1}$. Its dimensions are [ $MT^{−2}$ ]. The force acting per unit length in the plane of the interface between a liquid and any other surface is independent of the area of the interface.
Angle of Contact
The angle of contact is defined as the angle that the tangent to the liquid surface at the point of contact makes with the solid surface inside the liquid. The angle of contact depends on the nature of the solid and the liquid in contact. At the point of contact, the surface forces between the three media must be in equilibrium. See the figure given next.
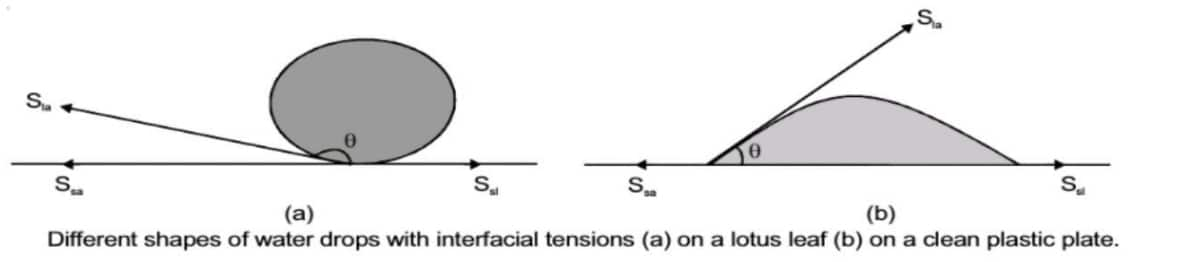
Drops in Fluids:
- A drop forms when a small amount of liquid is held together by surface tension.
- The spherical shape of a drop minimises surface area, making it the most energy-efficient form.
- The pressure inside a drop is slightly higher than the surrounding fluid due to its curved surface (as per Laplace's law).
Bubbles in Fluids:
A bubble is typically a gas enclosed in a thin film of liquid (like a soap bubble).
It has two surfaces (inner and outer), so the excess pressure inside is twice that of a single surface:
ΔP=4T/r
where T is surface tension and r is the radius of the bubble.
Capillary Rise
Capillary Rise is a phenomenon observed when a liquid climbs up a narrow tube against gravity. It happens due to the combination of cohesive forces (between liquid molecules) and adhesive forces (between liquid and tube walls).
When adhesive forces are stronger (like in water and glass), the liquid rises in the capillary tube.
The height of rise h is given by the formula:
h=2Tcosθ/rρg
where:
- T = surface tension of the liquid
- θ = angle of contact
- r = radius of the tube
- ρ = density of the liquid
- g = acceleration due to gravity
Buoyancy
-
When a body is partially or fully immersed in a fluid, an upward force acts on it and that upward force is called the buoyant force.
-
This whole phenomenon is known as Buoyancy.
-
The buoyant force acts at the centre of gravity of the liquid displaced by the immersed part of the body; that point is known as the centre of buoyancy.
Archimedes’ Principle
-
According to Archimedes' Principle, the liquid is displaced by the weight of the object when immersed fully or partially, and that weight is equal to the loss in weight when immersed in the liquid.
-
Let ‘T’ be the observed weight of a body with density σ, when it is fully immersed in the liquid of density p, then the original weight of that body, w = T / (1 – p / σ)
Laws of Flotation
-
Flotation of the object on a liquid surface requires that the mass of the object is similar to the mass of the liquid which is displaced by the immersion part of the body.
-
If we consider ‘W’ is the mass of a body and ‘w’ is the buoyant force acting on that body:
-
In the first case: W > w, the body will sink to the bottom of the liquid.
-
In the second case W < w, the body will float partially submerged in the liquid.
-
In the third case, W = w, the body will float in liquid
Conditions applicable for the stability of the body
For a stable equilibrium: The centre of buoyancy of the body lies vertically above the centre of gravity.
For unstable equilibrium: The centre of buoyancy of the body lies vertically above the centre of gravity.
For neutral equilibrium: The centre of buoyancy of the body coincides with the centre of gravity.
Class 11 Physics Chapter 9 Mechanical Properties of Fluids: Previous Year Questions and Answers
The chapter Mechanical Properties of Fluids explores how fluids behave under various conditions of pressure, flow, and deformation. It introduces fundamental concepts like density, pressure, Pascal’s law, viscosity, and surface tension. Understanding these ideas builds the foundation for real-life applications such as hydraulics, blood flow, aircraft design, and fluid dynamics. This chapter frequently appears in exams due to its strong conceptual and numerical focus.
Q1: A cube having a side of 10 cm with an unknown mass and a 200 gm mass was hung at two ends of a uniform rigid rod of 27 cm long. The rod, along with masses, was placed on a wedge, keeping the distance between the wedge point and the 200 gm weight as 25 cm. Initially, the masses were not in balance. A beaker is placed beneath the unknown mass, and water is added slowly to it. At a given point, the masses were in balance, and half the volume of the unknown mass was inside the water. (Take the density of the unknown mass is more than that of the water, the mass did not absorb water, and water density is $1 \mathrm{gm} / \mathrm{cm}^3$.) The unknown mass is ______ kg.
Answer:
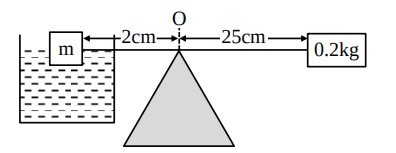
$\begin{aligned} & \text { Given, volume of block }=\left(10 \times 10^{-2}\right)^3=10^{-3} \mathrm{~m}^3 \\ & \text { Let density of block }=\rho \mathrm{kg} / \mathrm{m}^3 \\ & \text { mass of block }=\rho \times 10^{-3} \mathrm{~kg} \\ & \text { Buoyant Force }\left(\mathrm{F}_{\mathrm{B}}\right)=1000 \times \frac{10^{-3}}{2} \times 10=5 \mathrm{~N} \\ & \text { F.B.D. of blocks }\end{aligned}$
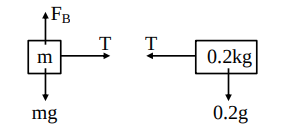
Balancing torque about point O, we get
$
\begin{aligned}
& \mathrm{mg}\left(2 \times 10^{-2}\right)-\mathrm{F}_{\mathrm{B}}\left(2 \times 10^{-2}\right)=0.2 \mathrm{~g}\left(25 \times 10^{-2}\right) \\
& \rho \times 10^{-3} \times 10 \times 2-10=50 \\
& \rho=3000 \mathrm{~kg} / \mathrm{m}^3 \\
& \text { Hence, mass of block }=\rho \times 10^{-3} =3000 \times 10^{-3}=3 \mathrm{~kg}
\end{aligned}
$
Hence, the answer is 3.
Q2:
A capillary tube of radius 0.1 mm is partly dipped in water (surface tension $70 \mathrm{dyne} / \mathrm{cm}$ and glass water contact angle $\simeq 0^{\circ}$ ) with $30^{\circ}$ inclined with vertical. The length of water risen in the capillary is _____ cm.
(Take $\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^2$ )
Answer:
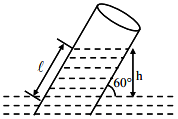
$\begin{aligned} & \mathrm{h}=\frac{2 \mathrm{~T} \cos \theta}{\rho \mathrm{gr}}=\frac{2 \times 70 \times 1}{1 \times 980 \times 10^{-2}} \\ & \mathrm{~h}=\frac{100}{7} \mathrm{~cm} \\ & \sin 60^{\circ}=\frac{\mathrm{h}}{\ell} \\ & \ell=\frac{\mathrm{h} \times 2}{\sqrt{3}} \\ & \ell=\frac{100}{7} \times \frac{2}{\sqrt{3}} \\ & =\frac{200}{7 \times \sqrt{3}} \\ & =16.49 \mathrm{~cm}\end{aligned}$
Q3:
The excess pressure inside a soap bubble A in air is half the excess pressure inside another soap bubble B in air. If the volume of the bubble A is $n$ times the volume of the bubble $B$, then, the value of $n$ is _____ .
Answer:
$\begin{aligned} & \Delta \mathrm{P}=\frac{4 \mathrm{~T}}{\mathrm{R}} \\ & \frac{\mathrm{R}_{\mathrm{A}}}{\mathrm{R}_{\mathrm{B}}}=\frac{\Delta \mathrm{P}_{\mathrm{B}}}{\Delta \mathrm{P}_{\mathrm{A}}}=2 \\ & \frac{\mathrm{~V}_{\mathrm{A}}}{\mathrm{V}_{\mathrm{B}}}=\left(\frac{\mathrm{R}_{\mathrm{A}}}{\mathrm{R}_{\mathrm{B}}}\right)^3=8\end{aligned}$
Hence, the answer is 8.
How to Master Class 11 Physics Chapter 9 Mechanical Properties of Fluids?
This chapter is not difficult to master when you concentrate on learning the behaviour of fluids and not on learning everything at the same time. Begin with an introductory knowledge of the fundamental terminology, including density, pressure, column of fluid, and buoyancy, to make the further concepts easier. The main points that must be studied to study this chapter are as follows:
- Learn fundamentals such as fluid pressure, the Pascal law and the Archimedes principle and the Bernoulli principle with simple real-life scenarios- such as the reason behind objects floating or the spouting of perfumes.
- Learn how to compare the ideal and real fluids, and this will make viscosity and streamline flow easier in the future.
- Revise and memorise the equations of pressure depth relationship, surface tension, excess pressure in drops/bubbles and terminal velocity.
- Draw clean drawings of streamlines, hydraulic lifts, capillary action and pressure change in order to enhance visual memory.
- Solve numerical problems on the Bernoulli equation, buoyancy, viscosity, and Reynolds number, as most questions of the exams are based on them.
- Use NCERT solved examples as a guide to understand how to write clear and step-wise solutions for board exams.
- Solve exercise questions, exemplar problems and previous year papers to identify the most frequently asked concepts and improve speed.
- Prepare a revision sheet containing a few formulas and important laws in a small size so that last-minute revision can be easy before exams.
Importance of Mechanical Properties of Fluids Class 11 Notes
The NCERT notes Class 11 Physics Chapter 9, Mechanical Properties of Fluids, are highly valuable for understanding how fluids behave in motion and at rest. These Mechanical Properties of Fluids Class 11 Physics notes help students strengthen their conceptual base on topics like pressure, buoyancy, and flow of liquids—crucial for exams like CBSE, JEE, and NEET. They make revision faster and easier by summarising formulas, derivations, and applications in a clear and concise manner.
- Strengthens Conceptual Understanding – Helps students clearly understand key concepts like pressure, buoyant force, Bernoulli’s principle, and viscosity.
- Exam-Focused Preparation – Covers all important topics and formulas as per the latest CBSE Class 11 Physics syllabus, making board exam preparation easier.
- Useful for Competitive Exams – Builds a strong foundation for JEE, NEET, and other entrance exams, where fluid mechanics problems are frequently asked.
- Simplifies Complex Topics – Explains tough derivations and concepts through step-by-step solutions, diagrams, and examples for better clarity.
- Quick Revision Resource – Concise and well-organised notes help students revise important formulas and principles in less time before exams.
- Real-Life Applications – Connects concepts like pressure, flow, and buoyancy with practical examples such as aeroplane flight, hydraulic systems, and submarine design.
NCERT Class 12 Notes Chapter-Wise
These NCERT Class 12 Physics notes provide a structured and comprehensive way to revise all chapters efficiently. Designed by subject experts, the notes simplify complex concepts, include important formulas, solved examples, and key points, making them ideal for quick revision. Students can access chapter-wise links to download PDFs, helping them study anytime and anywhere, whether for board exams or competitive exams like JEE and NEET.
Subject-Wise NCERT Exemplar Solutions
- NCERT Exemplar Class 11 Solutions
- NCERT Exemplar Class 11 Maths
- NCERT Exemplar Class 11 Physics
- NCERT Exemplar Class 11 Chemistry
- NCERT Exemplar Class 11 Biology
Subject-Wise NCERT Solutions
NCERT Books and Syllabus
Frequently Asked Questions (FAQs)
The key difference lies in the fluid's movement pattern. In streamline flow (also called laminar flow), fluid particles move in smooth, orderly layers or paths. The velocity at any given point remains constant. In contrast, turbulent flow is chaotic and unpredictable, with particles moving in irregular paths, forming swirls and eddies. This usually happens at higher speeds or when an obstacle is present.
While both are properties of fluids, they describe different things. Surface tension is a property of the liquid's surface, causing it to behave like a stretched membrane. It's why insects can stand on water. Viscosity, on the other hand, is a bulk property that relates to the entire fluid's resistance to flow or internal motion. In short, surface tension is a 'surface' phenomenon, while viscosity is an 'internal' phenomenon.
In Class 11 Physics chapter 9 notes we studied the concept that the height of the blood column inside the feet is more as compared to that for the brain, therefore, the blood exerts more pressure on the feet than on the brain.
P/ρ + v2/2 + gh = constant
According to Pascal’s law, the pressure exerted by the liquid is transmitted equally in all directions inside the liquid container. Hence, there is no fixed direction for the pressure to be applied in a particular direction. Thus, hydro static pressure is a scalar quantity.
Surface tension of the liquid is defined as the force acting per unit length.
Since the force which is in action, is independent of the area of the liquid surface, thus the surface tension is also independent of the area of the liquid surface. You can understand this by reading Mechanical Properties of Fluids Class 11 notes PDF download.
Variation in viscosity is given as follows:
ηt= η0/(1+αt+βt2 )
where η0 and ηt are coefficients of viscosity at 0°C and t°C, α and β are constants.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
