Waves Class 11th Notes - Free NCERT Class 11 Physics Chapter 15 Notes - Download PDF

NCERT Notes for Class 11 Chapter 14: Download PDF

The Class 11 Physics Chapter 14 Waves Notes give a concise, well-structured overview of all the key concepts, formulae and diagrams to revise in short. These Waves Class 11 Physics Chapter 14 CBSE notes assist you to revise quickly and exams and also enhance your comprehension without having to read the whole chapter once more. The PDF version of the notes will also enable one to access, save, or print the notes so that they can be revised again. They come in handy, particularly when one is doing things at the last moment and scoring well in the examination.

Download PDF

NCERT Notes for Class 11 Chapter 14

All the significant concepts, formulas, graphs, and definitions are introduced in Waves Class 11 Physics Chapter 14 CBSE notes in an easy and concise way. These Waves Class 11 Physics notes are useful in making a revision fast without having to read the entire textbook all over. They are meant to simplify the learning of exams by only emphasising the most important topics. To a well-organised point, these notes make the ultimate aid to quick revision and good grades.

Types of Waves

• The different types of waves can be broadly classified into three categories-

1. Mechanical waves: Mechanical waves can only be created or propagated in a material medium. Newton's laws of motion apply to these waves. For example, waves on the water's surface, waves on strings, sound waves, and so on.

2. Electromagnetic Waves: These are waves that are generated and propagated without the use of a material medium, such as a vacuum or any other material medium. Visible light, ultraviolet light, radio waves, and microwaves are examples of electromagnetic waves.

3. Matter waves: These waves are related to moving matter particles such as electrons, protons, and neutrons, among others.

• Furthermore, based on the direction of vibration, waves can be divided into two types-

1. Transverse wave motion: In transverse waves, the particles of the medium vibrate at right angles to the wave's propagation direction. String waves, surface water waves, and electromagnetic waves are examples of transverse waves. The oscillation of electric and magnetic fields at right angles to the wave's travel direction causes the disturbance that travels in electromagnetic waves (which includes light waves).

2. Longitudinal wave motion: In these types of waves, particles in the medium vibrate back and forth about their mean location along the energy propagation direction. Pressure waves are another name for them. Sound waves are mechanical waves that travel along a longitudinal axis.

Characteristics of Waves

• Characteristics of waves are-

(i) The particles in the medium traversed by a wave vibrate very slightly around their mean positions, but they are not permanently displaced in the propagation direction of the wave.

(ii) Each subsequent particle of the medium performs a motion that is nearly identical to its predecessors when viewed perpendicular to the wave's path of travel.

(iii) During wave motion, only energy is transferred, but not a piece of the medium.

• Wavelength: The wavelength is the distance travelled by the disturbance in the time it takes a medium particle to vibrate once. In the case of a transverse wave, a wavelength can alternatively be defined as the distance between two subsequent crests or troughs. A longitudinal wave's wavelength is equal to the distance between the centres of two compressions (or refractions).

• Amplitude: The largest displacement of the medium's particles from their mean position is the amplitude of a wave.

• Frequency: Frequency is defined as the number of vibrations produced by a particle in one second.

Unit of frequency - Hertz(Hz)

• Time Period: Time period refers to how long it takes a particle to complete one vibration.

• Wave Velocity: The time rate at which wave motion propagates in a given medium is referred to as wave velocity. It's not the same as particle velocity. The type of medium determines the wave velocity.

Wave velocity=frequency $\times$ wavelength

1. In a stretched string, the velocity of transverse waves is given by

$v=\sqrt{\frac{T}{\mu}}$

where T be the tension in the string and μ be the mass per unit length of the string,

2. In an elastic material, the longitudinal wave velocity is given by

$v=\sqrt{\frac{E}{\rho}}$

where E is the modulus of elasticity of the medium and ρ is the density of the medium

Newton’s Formula:

• According to Newton, when sound waves travel through air or a gaseous medium, they undergo isothermal change, and therefore, it is found that

$v=\sqrt{\frac{B_{\text {isothermal }}}{\rho}}=\sqrt{\frac{P}{\rho}}$

• According to Newton's formula, the speed of sound in air at STP conditions is 280 ms^-1. The empirically determined values, on the other hand, are 332 m/s.
• According to Laplace, the change occurs under adiabatic conditions during sound wave transmission because gases are thermal insulators and compressions and refractions alternate at a high frequency.

Factors Influencing the Velocity of Sound

• The velocity of sound in any gaseous medium is influenced by many factors such as density, pressure, temperature, humidity, wind velocity, and so on.
• In a gaseous state, the velocity of sound is inversely proportional to the square root of the gas's density.

(ii) If the temperature remains constant, the velocity of sound is unaffected by changes in gas pressure.

(iii) In a gas, sound velocity is proportional to the square root of the absolute temperature.

(iv) The sound velocity in moist air is larger than the sound velocity in dry air.

(v) If the wind is blowing at an angle θ to the sound propagation direction, the sound velocity is v+wcosθ, where w is the wind velocity.

General Equation of Progressive Waves

• A progressive wave travels in a given direction with constant amplitude.
• Because displacement is a function of both space and time in wave motion, the displacement relation is stated as a combination of position and time as:

$y(x, t)=A \sin (k x-\omega t+\phi)$

Relation Between Phase Difference And Path Difference

Phase difference= $(2 \pi / \lambda) \times$ path difference

The Principle of Superposition of Waves

The net displacement at a given time is the algebraic total of the displacements attributable to each wave at that moment when any number of waves meet concurrently at a point in a medium.

If y₁ and y₂ denote the movement of a particle caused by two separate waves. The resultant displacement at each point in the medium and at each instant of time is thus given by

$y-y_1+y_2$

Standing waves or Stationary waves

A new set of waves is created when two sets of progressive wave trains of the same kind (both longitudinal or both transverse) with the same amplitude and time period/frequency/ wavelength travelling at the same speed in opposite directions superimpose. These are referred to as stationary or standing waves.

The equation of a standing wave can be represented as follows:

$y=2 A \sin k x \cos \omega t$

Progressive Waves

1. The disturbance continues to spread, passing from particle to particle. Each particle vibrates in the same way as the one before it, but at a different rate.

2. The waves have crests and troughs, which are sine/cosine functions that travel with a specified velocity.

3. Each particle has the same amplitude, which it achieves in its own time as the wave progresses.

4. Every particle's phase changes from 0 to 2π on a constant basis.

5. No particle can be said to be at rest indefinitely. The particles are momentarily at rest twice during each vibration. At different moments, different particles reach this point.

6. All particles have the same maximum velocity, which they achieve one by one as the wave progresses.

7. Energy flows in a predictable pattern across all planes in the wave's propagation path.

Stationary Waves

1. The disturbance is stationary, as the wave does not move forward or backwards. Each particle has its own set of vibrational properties.

2. In each vibration, the waves resemble a sine/cosine function that shrinks to a straight line twice. It never moves forward.

3. Each particle has a specific amplitude. Some have no amplitude (nodes), whereas others constantly have maximum amplitude (anti-nodes). This is consumed by each participant at the same time.

4. One-half of the waves' particles have a fixed phase, while the other half of the waves' particles have the same phase in the opposite direction at the same time.

5. There are particles that are always at rest (nodes), and all other particles have a maximum movement that they all reach at the same time. In each vibration, these particles are momentarily at rest twice, all at the same time.

6. At the same time, all of the particles achieve their individual assigned velocities based on their positions. Two particles (nodes) in a wave form have constant zero velocities.

7. There is no energy movement in any direction across any plane. Each particle is given its own amount of energy. They all reach their RE. values at the same moment, and all energy becomes KB. at a later time.

8. Closed pipe and open pipe: In a closed pipe, one end is closed while the other is open. In an open pipe, both ends are open, having anti-nodes.

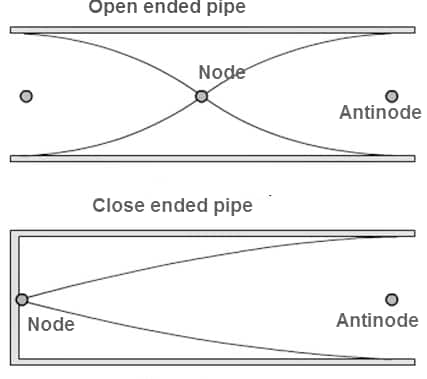
In a closed pipe, the frequency of the nth harmonic is f_n = nv/4L, where v is the velocity, L is the length

In an open pipe, the frequency of the nth harmonic is f_n = nv/2L

Frequency of the Stretched String

• In general, if the string vibrates in P loops, its frequency is given by

$v=\frac{P}{2 L} \sqrt{\frac{T}{\mu}}$

• Three rules of transverse vibrations of stretched strings emerge from this relationship. They are the laws of length, tension, and mass.

1. Law of Length: $v \propto \frac{1}{L}$

2. Law of Tension: $v \propto \sqrt{T}$

3. Law of Mass: $v \propto \frac{1}{\sqrt{\mu}}$

Beats

• Beats are the regular increase and fall in sound intensity that occur when two waves of almost equal frequencies move along the same line and in the same direction and superimpose each other.
• One beat is defined as a rise and fall in the intensity of sound, and the number of beats per second is known as beat frequency. It is written as follows:

$v_b=\left(v_1-v_2\right)$

Waves: Previous Year Question and Answer

Past Year Questions of the chapter Waves will give you an idea of the exact pattern of the exam, as well as the kind of questions that are asked the most. Questions in these are concerned with the motion of waves, relations of velocity, interference, beat, and Doppler effect-topics which are re-tested. PYQs enhance the level of your understanding of concepts, numerical ability, and accuracy. They also outline the areas that you have to focus on to score highly.

Q1: Which of the following statements are true for a stationary wave?

a) every particle has a fixed amplitude, which is different from the amplitude of its nearest particle

b) all the particles cross their mean position at the same time

c) all the particles are oscillating with the same amplitude

d) there is no net transfer of energy across any plane

e) there are some particles which are always at rest

Answer:

In a stationary wave, the particles between two nodes vibrate with different amplitude, which increases from node to antinode (0 to maximum) and decreases from antinode to node. The amplitude of particles varies with $\lambda$. The particles at a node are at rest, and hence there is no net transfer of energy. The particle between two nodes is in the same phase. The motion of particles between two nodes will be either upward or downward, crossing the mean position at the same time. Hence, statements a,b,d and e are correct.

Q2: The speed of sound waves in a fluid depends upon

(a) directly on the density of the medium.
(b) square of the Bulk modulus of the medium.
(c) inversely on the square root of density.
(d) directly on the square root of the bulk modulus of the medium.

Answer:

The speed of a sound wave in the fluid of bulk modulus K and density $\rho$ is given by

$
\begin{aligned}
& v=\sqrt{\frac{K}{\rho}} \\
& v \propto \sqrt{K} \text { (if } \rho \text { is constant) } \\
& v \propto \sqrt{\frac{1}{\rho}} \text { (if } \mathrm{K} \text { is constant) }
\end{aligned}
$

Hence, (c) and (d) options are correct.

Q3: A transverse harmonic wave on a string is described by $y(x, t)=3.0 \sin \left(36 t+0.018 x+\frac{\pi}{4}\right)$ where x and y are in cm and t is in s. The positive direction of x is from left to right.

(a) The wave is travelling from right to left.
(b) The speed of the wave is $20 \mathrm{~m} / \mathrm{s}$.
(c) The frequency of the wave is 5.7 Hz.
(d) The least distance between two successive crests in the wave is 2.5 cm.

Answer:

The standard form of a wave propagating in a positive direction

$
\begin{aligned}
& y=a \sin (\omega t-k x+\phi) \text { and } \\
& y=3.0 \sin \left(36 t+0.018 x+\frac{\pi}{4}\right)
\end{aligned}
$
A positive sign in the equation shows that the wave is travelling from right to left.

$\omega=36 ; 2 \pi \nu=36 \\$

$or \ v=\frac{36}{2 \pi}=\frac{18}{3.14}=5.7 \mathrm{~Hz} \\$
$ k=0.018=\frac{2 \pi}{\lambda} \\$
$ \lambda=\frac{2 \pi}{0.018} \\$
$ v=\nu \lambda=\frac{18}{\pi} \times \frac{2 \pi}{0.018}=\frac{2000 \mathrm{~cm}}{s}=\frac{20 \mathrm{~m}}{s}$
Distance between two successive crests $=\lambda=\frac{2 \pi}{0.018}=\frac{\pi}{0.009}=3.14 \times \frac{1000}{9}=\frac{3140}{9} \mathrm{~cm}=348.8 \mathrm{~cm}$

Hence, (a), (b) and (c) are the correct options.

How to Master Class 11 Physics Chapter 14 Waves?

Waves is concerned with the transmission of energy by periodic disturbances, and introduces such concepts as wave motion, speed, superposition, standing waves, and beats. The chapter relates mathematics to actual physical phenomena, which makes it conceptual and application-oriented. Having a clear knowledge about formulas, graphs and the behaviour of waves, this chapter becomes easy and very scoring. The secret of learning it is to practice the numericals regularly.

• Start by learning the simple concept of wave motion and the way the mechanical waves move in a medium through the oscillatory movements of the particles.
• Understand the difference between transverse and longitudinal waves using examples, because this is the basis of the entire chapter.
• Memorise the standard wave equation: $y=A \sin (k x-\omega t+\phi)$ and understand the meaning of amplitude, wavelength, frequency, phase, and angular frequency.
• Practised on numericals on wave speed using $v=\sqrt{T / \mu}$ for strings and $v=\sqrt{\gamma P / \rho}$ for gases, which are also common in exams.
• Learn about the superposition of waves and learn how waves combine mathematically to form constructive and destructive interference, and learn conditions of standing wave on strings and air columns and practise time period and frequency formulae of open and closed pipes.
• Learn beats effectively through working on problems that are based on two close frequencies, very prevalent in examinations.
• Plot wave diagrams like displacement-time and displacement-position curves to enhance your understanding of the behaviour of waves.
• Solve all NCERT textbook and NCERT Exemplar questions because many exam questions directly follow their pattern.
• Make a formula sheet on the wave velocity, conditions of interference, and frequency of standing waves, such that you can revise promptly.
• It is important to practise conceptual questions in order to grasp the variation of wave speed under the influence of changes in tension, mass per unit length, or air temperature.

Importance of Waves Class 11 Notes

Waves Class 11 Physics notes offer an easy-to-read, fast-revision version, which enables students to learn in a simplified form about a complicated topic such as wave motion, superposition, and standing waves. These NCERT notes Class 11 Physics Chapter 14 Waves bring out the most significant formulas, diagrams and concepts required during exams. They save time in revising and make the learning process more organised and efficient. These notes can aid students to score better, giving them brief explanations which enhance conceptual understanding.

• They give an organised review of all the most important concepts, including wavelength, frequency, amplitude and speed of a wave.
• The notes assist students to revise at a faster rate, particularly when it comes to exams, without having to read the entire NCERT chapter.
• Significant formulas, such as the speed of waves, frequencies of standing waves, are explained in a clear manner to be memorised easily.
• Wave propagation and interference patterns are easier to understand as they are represented in notes by diagrams and graphs.
• Notes highlight common exam questions and high-weightage topics, improving exam readiness.
• They also make it easier to understand because they give a good explanation of such terms as the phase difference, beats, nodes/antinodes.
• Notes assist in finding some solutions to numerical problems by describing the step-wise method of applying formulas.
• Notes are very useful, especially in competitive examinations such as JEE, since they give a summary of concepts in exam-oriented language.

NCERT Class 11 Notes Chapter-Wise

NCERT class 11 chapter-by-chapter notes are a systematic, simplified method of revising all the chapters within a short span of time and with ease. These notes provide important concepts, formulae, diagrams and definitions in a simple, understandable format. The presence of all the chapters with independent links will assist students in navigating the topics with ease and updating only what they require. This will be quicker, smarter and more efficient when exam preparation is concerned.

Subject-Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus