NCERT Class 11 Physics Chapter 9 Notes Mechanical Properties of Solids - Download PDF

NCERT Class 11 Physics Chapter 8 Notes: Download PDF

The NCERT Class 11 Physics Chapter 8 Notes PDF includes such important topics as stress, strain, Hooke's law, elastic moduli, and applications of elasticity in life as possible. These brief notes are simple to revise, save time and highly applicable to the CBSE board as well as competitive exams such as JEE and NEET.

Download PDF

NCERT Class 11 Physics Chapter 8 Notes

NCERT Class 11 Physics Chapter 8 Notes Mechanical Properties of Solids provide a brief but clear outline of how solids react to such forces as stretching, compression, hinging, and bending. These notes help students help in grasping some of the most important concepts, such as stress, strain, Hooke's law and are ideal for brushing up or revision and examinations.

Mechanical characteristics:-

1. Elasticity: Elasticity is a quality that allows an object to restore its original shape after an external force is removed. This implies it shows us how flexible a person's body is. Take, for example, a spring. When a spring is stretched, its shape changes, and when the external force is removed, the spring returns to its original position.

2. Plasticity is the opposite of elasticity. The term "property" refers to a state of permanent deformation. Even when the external force is eliminated, the object never returns to its previous shape. Plastic is the name for these types of items.

3. Ductility: It refers to the ability to be pulled into thin wires or sheets. for example:-Small gold

4. Strength: The ability to resist a high level of applied stress without failing.

Stress

• The restoring force per unit area is known as stress.
• When we apply an external force to the body in order to change its shape, the body creates a restoring force in the opposite direction.
• As an example, when an external force is applied to a rubber ball at the same time, the ball creates a force that acts in the opposite direction.
• The restoring force is the opposite force that arises in the ball when an external force is applied. Both forces have the same magnitude.

Stress = F/A (mathematically)

Where F is the restoring force that emerges in the body as a result of the force we apply.

A=area

• S.I. Unit:- N/m²

Longitudinal stress

• When a force is applied to the cross-sectional area of a cylindrical body, longitudinal stress is defined as the restoring force per unit area.

Shearing or Tangential Stress

• Force per unit area is restored when the applied force is parallel to the cross-sectional area of the body.
• There is relative displacement between the opposing faces of the body.

Volumetric Stress

• It produces a change in volume and density, shape remaining the same.

• It occurs in solids, liquids or gases

• In the case of fluids, only bulk stress can be found.

• It is equal to a change in pressure because the change in pressure is responsible for change in volume.

• Volume stress $=\frac{F}{A}=P$

Strain

• Strain is a deformation measurement that represents the displacement of particles in the body in relation to a reference length.
• It explains how and what happens to a body when it is put under stress.
• Mathematically:

Strain = ΔL/L, where ΔL is the length change.

L stands for the original length.

• Because it is a ratio of two quantities, it is a dimensionless quantity.

Strain Types:

1. Longitudinal Strain

• The longitudinal tension causes a change in the original length of the body. When we apply longitudinal stress to a body, the body either elongates or compresses as a result of the change in length. Longitudinal Strain is a measurement of length change.
• Longitudinal Strain = ΔL/L

2. Shearing Strain

• Shearing strain is the measurement of the relative displacement of the body's opposed faces as a result of shearing force. If we apply force parallel to the cross-sectional area, the opposite faces of the body will be displaced relative to each other. Shearing strain is a measurement of how far the two opposing faces have moved away from each other.
• Mathematically:-

Consider a cube with an initial length of L that is in a certain position and is shifted by an angle θ. Let x represent the modest relative displacement.

• Shearing strain= x/θ

3. Volume Strain

• The ratio of change in volume to the original volume as a result of hydraulic stress is known as volume strain. When a fluid applies stress to a body, the volume of the body changes without changing the shape of the body.
• Volume strain = ΔV/V

Hooke's Law

• Within the elastic limit, Hooke's law asserts that the stress developed is directly proportional to the strain produced in a body. Consider a situation in which the body is subjected to external force. As a result, tension arises in the body, and this stress causes a strain in the body, implying that the body will deform. Strain is formed as a result of stress.
• According to Hooke's law, as strain rises, so does stress, and vice versa. All elastic substances are subject to Hooke's law. It does not apply to the deformation of plastic. In terms of mathematics:

stress ∝ strain
stress = k × strain

The proportionality constant, k, is also known as the modulus of elasticity.

Stress-Strain Curve

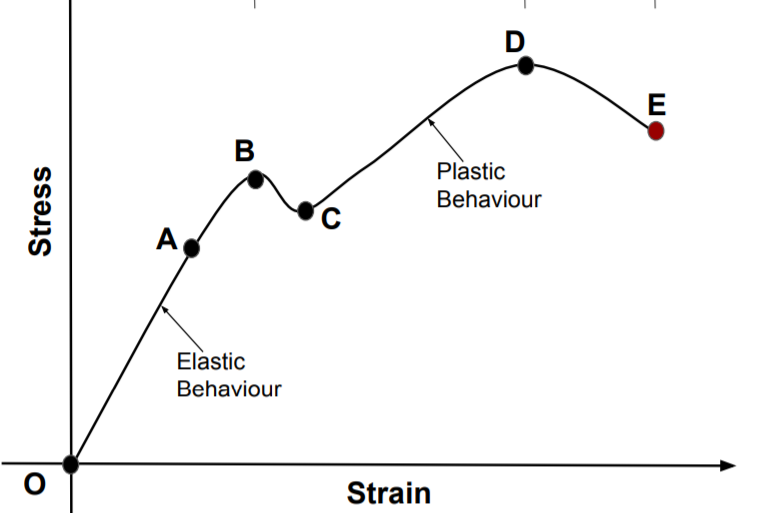
• It's a curve that depicts the relationship between stress and strain.
• The stress (which is the same magnitude as the applied force per unit area) and the strain produced are represented on a graph. The graph demonstrates how a specific material deforms as the load increases.
• The line that connects O and A is a straight line. This suggests that strain is directly related to stress. Hooke's Law is relevant in this area. The material behaves like an elastic body in this area.
• Stress and strain are not directly related in the region between A and B. However, as the force is withdrawn, the material returns to its original dimensions. They have elasticity to them.
• The yield point B(also known as the elastic limit) in the curve indicates that the material will be elastic until this point, and the stress corresponding to point B is known as the material's yield strength (Sy). The elastic region refers to the area between O and B.
• We can observe that even tiny changes in stress cause strain to increase rapidly from point B to point D. Even when the force is removed, the material does not return to its former location. Stress is zero at this stage, but strain is not, since the body has changed shape. Plastic deformation has occurred in the material. It is claimed that the substance is permanently fixed.
• The ultimate tensile strength (Su) of the material is shown by point D on the graph. We can observe that as we progress from D to E, tension reduces while strain increases. Finally, a fracture occurs at point E. This indicates that the body has broken down.

Modulus of Elasticity

• The elastic modulus is defined as the ratio of tension to strain. The elastic modulus is a property of each material.
• This means that gold will have a specific elastic modulus value, rubber will have a specific elastic modulus value, and so on.

Young’s Modulus

• Young's modulus is named after the physicist who first defined it.
• The ratio of longitudinal stress to longitudinal strain is known as the longitudinal stress-to-strain ratio.
• Y is the symbol for it.
• Y can be written as longitudinal stress/longitudinal strain = σ/ ε

Modulus of Shear (Modulus of Rigidity)

• The ratio of shearing stress to shearing strain is known as the shear modulus.
• Modulus of Rigidity is another name for it.
• The letter 'G' stands for it.
• G=shearing stress/shearing strain = (F/A)/( Δx/L) = FL/A Δx
• Relation between Young’s Modulus and Shear Modulus
• Young's modulus is greater than the shear modulus.
• G = Y/3 is there for most materials

Bulk Modulus

• The ratio of hydraulic stress to matching hydraulic strain is known as the bulk modulus.
• The letter 'B' stands for this.
• B = -p/(ΔV/V)

Here represents p =hydraulic stress, ΔV/V = hydraulic strain

• B(solids) > B(liquids) >B(gases)

• Compressibility: Compressibility refers to a substance's ability to withstand compression. Compressibility is the reciprocal of the bulk modulus.

The letter 'K' stands for this.

k=1/B = - (1/p) (ΔV/V)

k(solids)<k(liquids)<k(gases)

Work Done in Stretching the Wire

• When a body is in its natural shape, its potential energy corresponding to the molecular forces is minimum. When deformed, internal forces appear, and work has to be done against these forces. Thus, the potential energy of the body is increased. This is called the elastic potential energy.

$U=\frac{1}{2}\frac{YA}{L}(\mathrm{\Delta }L{)}^2$

We can also write,

$\begin{array}{r}W=\frac{1}{2}\left[\frac{YA\mathrm{\Delta }L}{L}\right]\mathrm{\Delta }L=\frac{1}{2}(\text{maximum stretching force})\times \text{extension}\\ W=\frac{1}{2}Y(AL){\left[\frac{\mathrm{\Delta }L}{L}\right]}^2=\frac{1}{2}\times Y\times \text{Volume}\times (\text{strain}{)}^2\end{array}$

Also, Potential energy per unit volume $=\frac{1}{2}\times$ strain $\times$ stress

Mechanical Properties of Solids: Previous Year Question and Answer

Q1: A mild steel wire of length 2L and cross-sectional area A is stretched, well within the elastic limit, horizontally between two pillars. Figure mass m is suspended from the midpoint of the wire. Strain in the wire is:

Answer:

$\begin{array}{r}\mathrm{\Delta }L=(AO+BO-AB)\\ \mathrm{\Delta }L=2[AO-L]\\ \mathrm{\Delta }L=2({(L^2+x^2)}^{\frac{1}{2}}-L)\end{array}$

$\begin{array}{r}\mathrm{\Delta }L=2L[1+\frac{x^2}{2L^2}-1]=\frac{x^2}{L}\\ \text{Strain}=\frac{\mathrm{\Delta }L}{2L}=\frac{x^2}{2L^2}\end{array}$

Q2: A rigid bar of mass M is supported symmetrically by three wires, each of length L. Those at each end are of copper, and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to:

Answer:

As the bar is supported symmetrically by the three wires, therefore extension in each wire is the same.
Let T be the tension in each wire, and the diameter of the wire is D, then Young's modulus is $Y=\frac{\text{Stress}}{\text{Strain}}$

$\begin{array}{r}Y=\frac{\frac{F}{A}}{\frac{\mathrm{\Delta }L}{L}}\\ Y=\frac{F}{A}\times \frac{L}{\mathrm{\Delta }L}\\ Y=\frac{F}{\pi {\left(\frac{D}{2}\right)}^2}\times \frac{L}{\mathrm{\Delta }L}\\ Y=\frac{4FL}{\pi D^2\mathrm{\Delta }L}\\ \Rightarrow D^2=\frac{4FL}{\pi \mathrm{\Delta }LY}\\ \Rightarrow D=\sqrt{\frac{4FL}{\pi \mathrm{\Delta }LY}}\end{array}$

As F and $\frac{L}{\mathrm{\Delta }L}$ are constants.
Hence,
$D\propto \sqrt{\frac{1}{Y}}$
or
$D=\frac{K}{\sqrt{Y}}$
Now, we can find the ratio as
$\frac{D_{\text{copper}}}{D_{\text{iron}}}=\sqrt{\frac{Y_{\text{iron}}}{Y_{\text{copper}}}}$

Q3: Consider two cylindrical rods of identical dimensions, one of rubber and the other of steel. Both rods are fixed rigidly at one end of the roof. A mass M is attached to each of the free ends at the centre of the rods. Then:

(a) Both the rods will elongate but there shall be no perceptible change in shape

(b) The steel rod will elongate and change shape but the rubber rod will only elongate

(c) The steel rod will elongate without any perceptible change in shape, but the rubber rod will elongate and the shape of the bottom edge will change to an ellipse

(d) The steel rod will elongate, without any perceptible change in shape, but the rubber rod will elongate with the shape of the bottom edge tapered to a tip at the centre

Answer:

$\to$ It is given that there are two cylindrical rods with identical dimensions and both attached with mass M at their respective centres.
$\to$ Both steel and rubber have different elastic properties.
$\to$ We know that steel is more elastic than rubber because the strain produced in rubber is greater than that of steel.

Thus, when mass $M$ is attached at the centre rubber will elongate with the change of the bottom edge tapered to a tip at the centre, while the steel will elongate, but there won't be any perceptible change in its shape.
Hence, the correct option is (d)

Importance of Mechanical Properties of Solids Class 11 Notes

Develops a Good Conceptual Base

• Class 11 Notes on the Mechanical Properties of Solids give a clear concept of such factors as stress, strain, elasticity, and Hooke's law. Such fundamentals are essential in solving higher-order Physics problems in Class 11 and Class 12.

Prerequisite to Competitive Exams

• Topics in NCERT Class 11 Physics Chapter 8 Notes will be directly applicable in the examination, like JEE Main, JEE Advanced, and NEET. Commonly, numerical questions are asked on elasticity, Young modulus, and stress-strain curves.

Simplifies Complex Topics

• Using the succinct NCERT Class 11 Physics notes, students will be able to learn the hard things (elastic moduli (Young's modulus, Bulk modulus, Shear modulus) and Poisson's ratio) within a few hours with simplified explanations and formulae.

Saves Time During Revision

• Properly organised Mechanical Properties of Solids Class 11 notes assist students to revise in a short period of time before examinations so that they do not miss out on crucial definitions, derivations and graphs.

Enhances Problem-Solving

• Answering examples and solving problems covered in Chapter 8 Notes covering Class 11 Physics enhances analysis abilities and gives confidence in writing board exams and entrance tests.

Connects Physics to Real-World Use

• The chapter demonstrates how principles such as elasticity and the relations between stress and strain are used in the construction of bridges, railway tracks, and aircraft. Such practical associations in real life render the study of Physics interesting and feasible.

Serves as a Consistent Exam Tool

• The Mechanical Properties of Solids Class 11 Notes are developed according to the most recent CBSE syllabus, and, thus, they are a reliable source of achieving high marks at school exams as well as getting ready to work in the engineering and medical spheres.

NCERT Class 11 Notes Chapter-Wise

NCERT Class 11 Notes Chapter-Wise are specially crafted to offer efficient study material to help students prepare exams effectively and with ease. These notes are divided into all the chapters of Physics as per the most recent CBSE syllabus with significant formulas, definitions, diagrams, and main ideas. The ability to provide chapter-wise links makes students faster, smarter and stress-free in their revision because the topics needed can be accessed quickly.

Subject-Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus