What Is Hooke's Law for Stress and Strain
Stress and Strain relationship shows a similar pattern when we study the behaviour of springs and their elasticity. Hooke’s Law gives the mathematical relationship between the stress and strain in a spring system. According to Hooke's Law, for small deformations, the stress and strain are almost proportional to each other, showing a linear relationship

In simpler terms, Hooke’s Law states that the strain caused in the material is directly proportional to the stress applied, and the stress applied must be in the elastic limit of the material.
On applying the stress, atoms and molecules in the elastic material get deformed and when the stress is removed, atoms and molecules get back to their initial position.
Hooke’s law is represented by:
F = - kx
Where, F represents the force exerted, x represents the extension in length and k is the proportionality constant which is also known as the spring constant having unit N/m.
Hooke’s Law Experiment
Hooke’s experiment using the spring system before giving the stress and strain relationship. The below figure shows the experiment apparatus where stress is applied on the spring in increasing order.
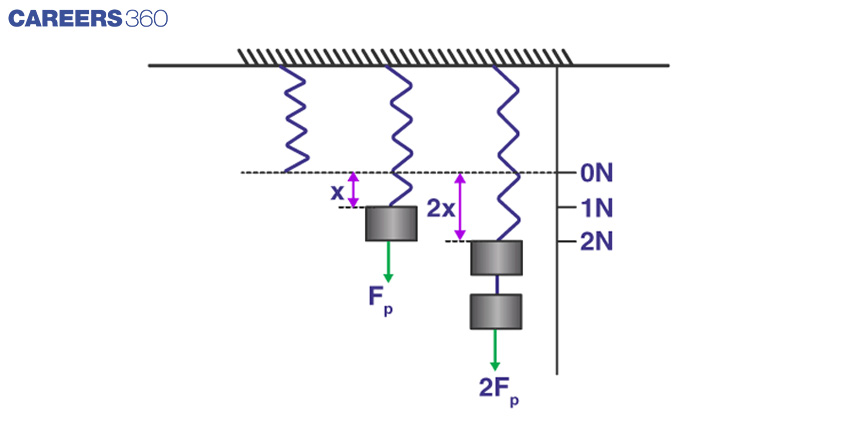
In the above figure, When no load is applied to the spring, it is in a stable condition. When a load of 1 N is applied, it gets elongated to a length of x and when the load of 2N is applied, it gets elongated to the 2x length. Spring constants are different for different springs which depends on the material of the spring.
In the above figure, 3 instances are shown which are :
Stable condition of the spring in which the spring is elongated to a length of x under a load of 1 N, and the spring elongated to a length of 2x under a load of 2 N. Spring constant of the spring can be calculated if these values are substituted in the Hooke’s law equation.
Also, check - Best Summer Schools In The World
Young’s Modulus
Modulus of elasticity is represented by Young’s Modulus. It represents the resilience of a material when mechanical force is applied. Young's Modulus is denoted by Y and is measured for the mechanical properties of rods, wires etc. The relationship between Stress and Strain is represented by Young's Modulus and Mathematically it is represented by:
Young’s Modulus= Stress / Strain
This ratio tells us how easily a material can be stretched and deformed. Here stress is the amount of force applied on the material per unit area and strain is the extension in length.
The important property of the Young’s Modulus is that it applies to linear objects in the elastic range only. Formula for Young’s Modulus can be used to solve many numerical problems.
Stress-Strain Curve for Low Carbon Steel
One of the important curves in the NCERT syllabus of Hooke’s Law is the stress-strain curve for low carbon steel. As from the figure below showing the stress and strain relationship, it can be seen that the material exhibits the elastic behaviour till the yield strength point, after which the material loses elasticity and the relationship between stress and strain is not linear. After elasticity, the material exhibits plasticity.
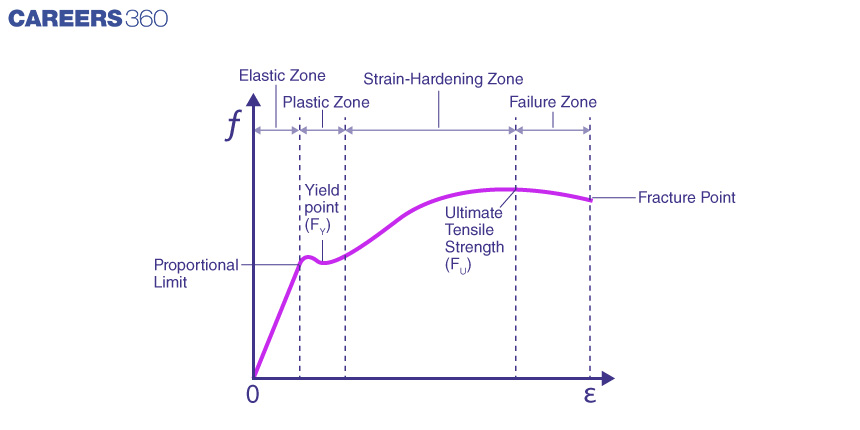
When the stress and strain are proportional, from the origin to the limit nearing yield strength, the straight line relationship implies that the material follows Hooke’s law and the material is in the elastic range. Once the stress is extended beyond the elastic limit the material loses its elasticity and exhibits plasticity. The area under the curve which is formed by the stress-strain relationship from the origin to the proportional limit belongs to the elastic range. The area under the curve from a proportional limit to the fracture point shown on the graph belongs to the plastic range.
The ultimate strength of the material is assessed by the ordinary value of the stress-strain curve calculated from the origin to the rupture point.
Applications of Hooke’s Law
Hooke’s law provides a mathematical relationship between stress and strain which is used in the mechanical industry and various devices. Below are some of the important applications:
Hooke’s Law is used as a fundamental principle behind the manometer which is used to measure the pressure difference, it is used in the spring scale and the balance wheel of a clock.
Hooke's law has applications in seismology and molecular mechanics.
Important Questions
Following are some of the important questions and their answers in brief related to Hooke’s Law that are included in the Board exams.
Do all materials follow Hooke’s Law ?
Hooke’s Law is applied to the objects which are elastic in nature. Beyond the elastic limit, Hooke’s law doesn't apply to the objects.
What is the nature of graphs of Hooke’s Law?
Hooke’s Law as shown in the above graph shows a linear relationship. According to Hooke’s law, the restoring force is proportional to the displacement of the object.
Beyond which limit, Hooke’s Law fails?
Hooke’s law is applied to perfectly elastic materials and does not apply beyond the elastic limit of materials. Hence beyond the elastic limit, Hooke's Law fails.
What is the use of Hooke’s Law?
Hooke’s Law is used in multiple industries as it helps us understand the stretchability of an object when it is stretched or compressed.
List out the various types of strain
Following are the types of strains:
Longitudinal Strain
Volumetric Strain
Shear Strain
JEE Mains Previous Year Questions
Q-1 (JEE Main 2022)
The elastic behaviour of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of ![]() ________
________![]() . Assume that material is elastic upto the linear strain of
. Assume that material is elastic upto the linear strain of ![]()
.jpg)
Answer = 25
Solution:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Concepts Used:
Concept to calculate slope of a straight line graph
stress - strain relation of hooke’s law
Concept of relation between energy density, stress and strain
Q-2 (JEE Main 2022)
A metal wire of length ![]() and cross-sectional area
and cross-sectional area ![]() has breaking stress
has breaking stress ![]() . A block of is attached at one end of the string and is rotating in a horizontal circle. The maximum linear velocity of block will be__________
. A block of is attached at one end of the string and is rotating in a horizontal circle. The maximum linear velocity of block will be__________ ![]()
Answer = 50
Solution:
![]()
![]()
![]()
.jpg)
![]()
![]()
![]()
![]()
![]()
![]()
The maximum linear velocity will be ![]()
Concept used
Centrifugal force
Concept to calculate stress
Q-3 (JEE Main 2021)
Wires ![]() are made of same material having the breaking stress of
are made of same material having the breaking stress of ![]() have cross-sectional area of
have cross-sectional area of ![]() , respectively. Masses of
, respectively. Masses of ![]() hang from them as shown in the figure. The maximum mass that can be placed in the pan without breaking the wires is _______kg.
hang from them as shown in the figure. The maximum mass that can be placed in the pan without breaking the wires is _______kg. ![]()
.jpg)
Answer = 40 Kg
Solution:
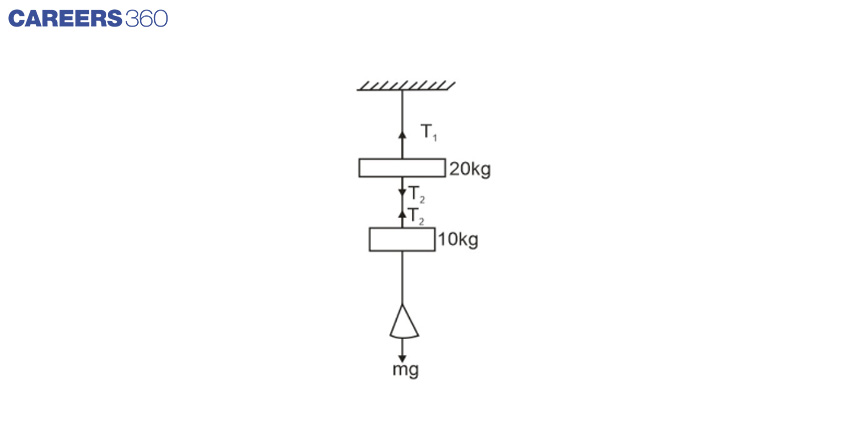
![]() ......(1)
......(1)
![]() .......(2)
.......(2)
![]()
![]()
![]()
For wire 1
![]()
![]()
![]()
![]()
![]()
Maximum mass in pan wire 1 can beat is 70kg
For wire 2
![]()
![]()
![]()
![]()
Maximum mass in pan wire 2 can bear is 40kg
Concepts Used:
Concept to find out tension
Concept of stress and breaking stress
We have discussed in brief about the spring force formula and the Hooke’s law of the spring along with the graphical representation of the spring force equation. Hooke’s law gives a better understanding of the concept of spring and its elastic behaviour and this concept is helpful in understanding the working principle of the mechanical devices.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
