NCERT Solutions for Class 11 Maths Chapter 8 Sequences and Series

Question 1: Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

$a _n = n ( n +2)$

Answer:

Given : $a _n = n ( n +2)$

$a _1 = 1 ( 1 +2)=3$

$a _2 = 2 ( 2 +2)=8$

$a _3 = 3 ( 3 +2)=15$

$a _4 = 4 ( 4 +2)=24$

$a _5 = 5 ( 5 +2)=35$

Therefore, the required number of terms = 3, 8, 15, 24, 35

Question 2: Write the first five terms of each of the sequences in Exercises 1 to 6 whose terms are:

$a _n = \frac{n }{n+1}$

Answer:

Given : $a _n = \frac{n }{n+1}$

$a _1 = \frac{1}{1+1}=\frac{1}{2}$

$a _2 = \frac{2}{2+1}=\frac{2}{3}$

$a _3 = \frac{3}{3+1}=\frac{3}{4}$

$a _4 = \frac{4}{4+1}=\frac{4}{5}$

$a _5 = \frac{5}{5+1}=\frac{5}{6}$

Therefore, the required number of terms $\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6}$

Question 3: Write the first five terms of each of the sequences in Exercises 1 to 6 whose terms are:

$a _ n = 2 ^n$

Answer:

Given : $a _ n = 2 ^n$

$a _ 1 = 2 ^1=2$

$a _ 2 = 2 ^2=4$

$a _ 3 = 2 ^3=8$

$a _ 4 = 2 ^4=16$

$a _ 5 = 2 ^5=32$

Therefore, the required number of terms $=2,4,8,16,32.$

Question 4: Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

$a _n = \frac{2n-3 }{6}$

Answer:

Given : $a _n = \frac{2n-3 }{6}$

$a _1 = \frac{2\times 1-3 }{6}=\frac{-1}{6}$

$a _2 = \frac{2\times 2-3 }{6}=\frac{1}{6}$

$a _3 = \frac{2\times 3-3 }{6}=\frac{3}{6}=\frac{1}{2}$

$a _4 = \frac{2\times 4-3 }{6}=\frac{5}{6}$

$a _5 = \frac{2\times 5-3 }{6}=\frac{7}{6}$

Therefore, the required number of terms $=\frac{-1}{6},\frac{1}{6},\frac{1}{2},\frac{5}{6},\frac{7}{6}$

Question 5: Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

$a _ n = ( -1) ^{n-1} 5 ^{n+1}$

Answer:

Given : $a _ n = ( -1) ^{n-1} 5 ^{n+1}$

$a _ 1 = ( -1) ^{1-1} 5 ^{1+1}=(-1)^{0}.5^2=25$

$a _ 2 = ( -1) ^{2-1} 5 ^{2+1}=(-1)^{1}.5^3=-125$

$a _ 3 = ( -1) ^{3-1} 5 ^{3+1}=(-1)^{2}.5^4= 625$

$a _ 4 = ( -1) ^{4-1} 5 ^{4+1}=(-1)^{3}.5^5= -3125$

$a _ 5 = ( -1) ^{5-1} 5 ^{5+1}=(-1)^{4}.5^6= 15625$

Therefore, the required number of terms $=25,-125,625,-3125,15625$

Question 6: Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

$a _n = n \frac{n^2 + 5}{4}$

Answer:

Given : $a _n = n \frac{n^2 + 5}{4}$

$a _1 = 1. \frac{1^2 + 5}{4}=\frac{6}{4}=\frac{3}{2}$

$a _2 = 2. \frac{2^2 + 5}{4}=\frac{18}{4}=\frac{9}{2}$

$a _3 = 3. \frac{3^2 + 5}{4}=\frac{42}{4}=\frac{21}{2}$

$a _4 = 4. \frac{4^2 + 5}{4}=\frac{84}{4}=21$

$a _5 = 5. \frac{5^2 + 5}{4}=\frac{150}{4}=\frac{75}{2}$

Therefore, the required number of terms $=\frac{3}{2},\frac{9}{2},\frac{21}{2},21,\frac{75}{2}$

Question 7: Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

$a _ n = 4 n - 3 ; a _{17} , a _{24}$

Answer:

$a _ n = 4 n - 3$

Put $n=17,$

$a_{17}=4 \times 17-3=68-3=65$

Put n = 24,

$a_{24}=4 \times 24-3=96-3=93$

Hence, we have $a_{17}=65$ and $a_{24}=93.$

Question 8: Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

$a _n = \frac{n^2 }{2^n } ; a_7$

Answer:

Given : $a _n = \frac{n^2 }{2^n }$

Put n=7,

$a _7 = \frac{7^2 }{2^7 } =\frac{49}{128}$

Hence, we have $a _7 =\frac{49}{128}$

Question 9: Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

$a _ n = ( -1) ^{n-1} n ^ 3 , a _9$

Answer:

Given : $a _ n = ( -1) ^{n-1} n ^ 3$

Put n = 9,

$a _ 9 = ( -1) ^{9-1} 9 ^ 3= (1).(729)=729$

The value of $a _ 9 =729$

Question 10: Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

$a _n = \frac{n ( n-2)}{ n+3 }; a _{20}$

Answer:

Given : $a _n = \frac{n ( n-2)}{ n+3 }$

Put n = 20,

$a _{20} = \frac{20 ( 20-2)}{ 20+3 }=\frac{360}{23}$

Hence, value of $a _{20}=\frac{360}{23}$

Question 11: Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series:

$a_1 = 3, a_n = 3a_{n - 1} + 2\: \: for \: \: all \: \: n > 1$

Answer:

Given : $a_1 = 3, a_n = 3a_{n - 1} + 2\: \: for \: \: all \: \: n > 1$

$a_2 = 3a_{2 - 1} + 2=3a_1+2=3(3)+2=11$

$a_3 = 3a_{3 - 1} + 2=3a_2+2=3(11)+2=35$

$a_4 = 3a_{4 - 1} + 2=3a_3+2=3(35)+2=107$

$a_5 = 3a_{5 - 1} + 2=3a_4+2=3(107)+2=323$

Hence, the five terms of the series are $3,11,35,107,323$

Series $=3+11+35+107+323+...............$

Question 12: Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series:

$a _ 1 = -1 , a _ n = \frac{a_{n-1}}{n} , n \geq 2$

Answer:

Given : $a _ 1 = -1 , a _ n = \frac{a_{n-1}}{n} , n \geq 2$

$a _ 2 = \frac{a_{2-1}}{2} =\frac{a_1}{2}=\frac{-1}{2}$

$a _ 3 = \frac{a_{3-1}}{3} =\frac{a_2}{3}=\frac{-1}{6}$

$a _ 4 = \frac{a_{4-1}}{4} =\frac{a_3}{4}=\frac{-1}{24}$

$a _ 5 = \frac{a_{5-1}}{5} =\frac{a_4}{5}=\frac{-1}{120}$

Hence, five terms of series are $-1,\frac{-1}{2},\frac{-1}{-6},\frac{-1}{24},\frac {-1}{120}$

Series

$=-1+\frac{-1}{2}+\frac{-1}{-6}+\frac{-1}{24}+\frac {-1}{120}.........................$

Question 13: Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series: $a_1 = a_2 = 2, a_n = a_{n - 1}-1, n > 2$

Answer:

Given : $a_1 = a_2 = 2, a_n = a_{n - 1}-1, n > 2$

$a_3 = a_{3 - 1}-1=a_2-1=2-1=1$

$a_4 = a_{4 - 1}-1=a_3-1=1-1=0$

$a_5 = a_{5 - 1}-1=a_4-1=0-1=-1$

Hence, the five terms of the series are $2,2,1,0,-1$

Series $=2+2+1+0+(-1)+..................$

Question 14: The Fibonacci sequence is defined by $1 = a _ 1 = a _2 \: \:and \: \: a _n = a _{n-1} + a _{n-2} , n > 2$

Find $\frac{a _{n+1}}{a_n}$ , for n = 1, 2, 3, 4, 5

Answer:

Given: The Fibonacci sequence is defined by $1 = a _ 1 = a _2 \: \:and \: \: a _n = a _{n-1} + a _{n-2} , n > 2$

$a _3 = a _{3-1} + a _{3-2} =a_2+a_1=1+1=2$

$a _4 = a _{4-1} + a _{4-2} =a_3+a_2=2+1=3$

$a _5 = a _{5-1} + a _{5-2} =a_4+a_3=3+2=5$

$a _6 = a _{6-1} + a _{6-2} =a_5+a_4=5+3=8$

$For \,\,n=1,\frac{a _{n+1}}{a_n}=\frac {a_{1+1}}{a_1}=\frac{a_2}{a_1}=\frac{1}{1}=1$

$For \,\, n=2,\frac{a _{n+1}}{a_n}=\frac {a_{2+1}}{a_2}=\frac{a_3}{a_2}=\frac{2}{1}=2$

$For \,\, n=3,\frac{a _{n+1}}{a_n}=\frac {a_{3+1}}{a_3}=\frac{a_4}{a_3}=\frac{3}{2}$

$For \,\, n=4,\frac{a _{n+1}}{a_n}=\frac {a_{4+1}}{a_4}=\frac{a_5}{a_4}=\frac{5}{3}$

$For \,\, n=5,\frac{a _{n+1}}{a_n}=\frac {a_{5+1}}{a_5}=\frac{a_6}{a_5}=\frac{8}{5}$

Question 1: Find the $20 ^{th}$ and $n ^{th}$ terms of the G.P. $\frac{5}{2},\frac{5}{4},\frac{5}{8},....$

Answer:

G.P :

$\frac{5}{2},\frac{5}{4},\frac{5}{8},....$

first term = a

$a=\frac{5}{2}$

common ratio = r

$r=\frac{\frac{5}{4}}{\frac{5}{2}}=\frac{1}{2}$

$a_n=a.r^{n-1}$

$\Rightarrow$$a_{20}=\frac{5}{2}.(\frac{1}{2})^{20-1}$

$\Rightarrow$$a_{20}=\frac{5}{2}.(\frac{1}{2^{19}})$

$\Rightarrow$$a_{20}=\frac{5}{2^{20}}$

$a_n=a.r^{n-1}$

$\Rightarrow$$a_n=\frac{5}{2}.\left ( \frac{1}{2} \right )^{n-1}$

$\Rightarrow$$a_n=\frac{5}{2}. \frac{1}{2^{n-1}}$

$\Rightarrow$$a_n=\frac{5}{2^n}$ the nth term of G.P

Question 2: Find the $12 ^{th}$ term of a G.P. whose $8 ^{th}$ term is 192 and the common ratio is 2.

Answer:

First term = a

common ratio = r = 2

$8 ^{th}$ term is 192

$a_n=a.r^{n-1}$

$\Rightarrow$$a_8=a.(2)^{8-1}$

$\Rightarrow$$192=a.(2)^{7}$

$\Rightarrow$$a=\frac{2^6.3}{2^7}$

$\Rightarrow$$a=\frac{3}{2}$

$a_n=a.r^{n-1}$

$\Rightarrow$$a_{12}=\frac{3}{2}. ( 2 )^{12-1}$

$\Rightarrow$$a_{12}=\frac{3}{2}. ( 2 )^{11}$

$\Rightarrow$$a_{12}= 3. ( 2 )^{10}$

$\Rightarrow$$a_{12}= 3072$ is the $12 ^{th}$ term of a G.P.

Question 3: The $5 ^{th}, 8 ^{th} \: \ and nd \: \: 11 ^{th}$ terms of a G.P. are p, q, and s, respectively. Show that $q ^2 = ps$

Answer:

To prove : $q ^2 = ps$

Let first term and common ratio = r

$a_5=a.r^4=p..................(1)$

$a_8=a.r^7=q..................(2)$

$a_{11}=a.r^{10}=s..................(3)$

Dividing equation 2 by 1, we have

$\frac{a.r^7}{a.r^4}=\frac{q}{p}$

$\Rightarrow r^3=\frac{q}{p}$

Dividing equation 3 by 2, we have

$\frac{a.r^{10}}{a.r^7}=\frac{s}{q}$

$\Rightarrow r^3=\frac{s}{q}$

Equating values of $r^3$ , we have

$\frac{q}{p}=\frac{s}{q}$

$\Rightarrow q^2=ps$

Hence proved.

Question 4: The $4^{th}$ term of a G.P. is the square of its second term, and the first term is -3. Determine its $7^{th}$ term.

Answer:

First term =a= -3

$4^{th}$ term of a G.P. is the square of its second term

$\Rightarrow a_4=(a_2)^2$

$\Rightarrow a.r^{4-1}=(a.r^{2-1})^2$

$\Rightarrow a.r^{3}=a^2.r^{2}$

$\Rightarrow r=a=-3$

$a_7=a.r^{7-1}$

$\Rightarrow a_7=(-3).(-3)^{6}$

$\Rightarrow a_7=(-3)^{7}=-2187$

Thus, the seventh term is -2187.

Question 5: Which term of the following sequences:

(a) $2,2\sqrt 2 , 4 .,....is \: \: 128 ?$

(b) Which term of the following sequences: $\sqrt 3 ,3 , 3 \sqrt 3 ,...is \: \: 729 ?$

(c) Which term of the following sequences: $\frac{1}{3} , \frac{1}{9} , \frac{1}{27} ,....is \: \: \frac{1}{19683}?$

Answer:

(a) Given : $GP = 2,2\sqrt 2 , 4 .,............$

$a=2\, \, \, \, \, and \, \, \, \, \, r=\frac{2\sqrt{2}}{2}=\sqrt{2}$

nth term is given as 128.

$a_n=a.r^{n-1}$

$\Rightarrow 128=2.(\sqrt{2})^{n-1}$

$\Rightarrow 64=(\sqrt{2})^{n-1}$

$\Rightarrow 2^6=(\sqrt{2})^{n-1}$

$\Rightarrow \sqrt{2}^{12}=(\sqrt{2})^{n-1}$

$\Rightarrow n-1=12$

$\Rightarrow n=12+1=13$

The 13th term is 128.

(b) Given : $GP=\sqrt 3 ,3 , 3 \sqrt 3 ,........$

$a=\sqrt{3}\, \, \, \, \, and \, \, \, \, \, r=\frac{3}{\sqrt{3}}=\sqrt{3}$

n The term is given as 729.

$a_n=a.r^{n-1}$

$\Rightarrow 729=\sqrt{3}.(\sqrt{3})^{n-1}$

$\Rightarrow 729=(\sqrt{3})^{n}$

$\Rightarrow( \sqrt{3})^{12}=(\sqrt{3})^{n}$

$\Rightarrow n=12$

The 12th term is 729.

(c) Given : $GP=\frac{1}{3} , \frac{1}{9} , \frac{1}{27} ,............$

$a=\frac{1}{3}\, \, \, \, \, and \, \, \, \, \, r=\frac{\frac{1}{9}}{\frac{1}{3}}=\frac{1}{3}$

nth term is given as $\frac{1}{19683}$

$a_n=a.r^{n-1}$

$\Rightarrow \frac{1}{19683}=\frac{1}{3}.(\frac{1}{3})^{n-1}$

$\Rightarrow \frac{1}{19683}=\frac{1}{3^n}$

$\Rightarrow \frac{1}{3^9}=\frac{1}{3^n}$

$\Rightarrow n=9$

Thus, n = 9.

Question 6: For what values of x, the numbers $-\frac{2}{7} ,x, -\frac{7}{2}$ are in G.P.?

Answer:

$GP=-\frac{2}{7} ,x, -\frac{7}{2}$

Common ratio = r.

$r=\frac{x}{\frac{-2}{7}}=\frac{\frac{-7}{2}}{x}$

$\Rightarrow x^2=1$

$\Rightarrow x=\pm 1$

Thus, for $x=\pm 1$, the numbers will be in GP.

Question 7: Find the sum of the indicated number of terms in each of the geometric progressions in 0.15, 0.015, 0.0015, ... 20 terms.

Answer:

Geometric progressions are 0.15, 0.015, 0.0015, ... .....

a = 0.15 , r = 0.1 , n = 20

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$S_{20}=\frac{0.15(1-(0.1)^{20})}{1-0.1}$

$\Rightarrow$$S_{20}=\frac{0.15(1-(0.1)^{20})}{0.9}$

$\Rightarrow$$S_{20}=\frac{0.15}{0.9}(1-(0.1)^{20})$

$\Rightarrow$$S_{20}=\frac{15}{90}(1-(0.1)^{20})$

$\Rightarrow$$S_{20}=\frac{1}{6}(1-0.1^{20})$

Question 8: Find the sum to the indicated number of terms in each of the geometric progressions in $\sqrt 7, \sqrt {21}, 3 \sqrt 7,.... n \: \: terms$

Answer:

$GP=\sqrt 7 , \sqrt {21} , 3 \sqrt 7 ,...............$

$a=\sqrt{7}\, \, \, \, and\, \, \, \, \, r=\frac{\sqrt{21}}{\sqrt{7}}=\sqrt{3}$

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$S_n=\frac{\sqrt{7}(1-\sqrt{3}^n)}{1-\sqrt{3}}$

$\Rightarrow$$S_n=\frac{\sqrt{7}(1-\sqrt{3}^n)}{1-\sqrt{3}}\times \frac{1+\sqrt{3}}{1+\sqrt{3}}$

$\Rightarrow$$S_n=\frac{\sqrt{7}(1-\sqrt{3}^n)}{1-3} (1+\sqrt{3})$

$\Rightarrow$$S_n=\frac{\sqrt{7}(1-\sqrt{3}^n)}{-2} (1+\sqrt{3})$

$\Rightarrow$$S_n=\frac{\sqrt{7}(1+\sqrt{3})}{2} (\sqrt{3}^n-1)$

Question 9: Find the sum to the indicated number of terms in each of the geometric progressions in $-a, a^, - a ^3, ... n terms ( if a \neq -1)$

Answer:

The sum to the indicated number of terms in each of the geometric progressions is:

$GP=1,-a , a^2 , - a ^3 , .............$

$a=1\, \, \, and\, \, \, \, r=-a$

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$S_n=\frac{1(1-(-a)^n)}{1-(-a)}$

$\Rightarrow$$S_n=\frac{1(1-(-a)^n)}{1+a}$

$\Rightarrow$$S_n=\frac{1-(-a)^n}{1+a}$

Question 10: Find the sum to the indicated number of terms in each of the geometric progressions in $x ^3, x^5, x^7 ... n \: \: terms (if \: \: x \neq \pm 1)$

Answer:

$GP=x ^3 , x^5 , x^7 .....................$

$a=x^3\, \, \, and\, \, r=\frac{x^5}{x^3}=x^2$

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$S_n=\frac{x^3(1-(x^2)^n)}{1-x^2}$

$\Rightarrow$$S_n=\frac{x^3(1-(x^2)^n)}{1-x^2}$

Question 11: Evaluate $\sum_{k = 1}^{11} ( 2+ 3 ^k )$

Answer:

Given :

$\sum_{k = 1}^{11} ( 2+ 3 ^k )$

$\Rightarrow$$\sum_{k = 1}^{11} ( 2+ 3 ^k )=\sum _{k=1}^{11}2 +\sum _{k=1}^{11} 3^k$

$=22 +\sum _{k=1}^{11} 3^k...............(1)$

$\Rightarrow$$\sum _{k=1}^{11} 3^k=3^1+3^2+3^3+....................3^{11}$

These terms form GP with a = 3 and r = 3.

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$S_n=\frac{3(1-3^{11})}{1-3}$

$\Rightarrow$$S_n=\frac{3(1-3^{11})}{-2}$

$\Rightarrow$$S_n=\frac{3(3^{11}-1)}{2}$ $=\sum _{k=1}^{11} 3^k$

$\Rightarrow$$\sum_{k = 1}^{11} ( 2+ 3 ^k )$ $=22+\frac{3(3^{11}-1)}{2}$

Question 12: The sum of the first three terms of a G.P. is $\frac{39}{10}$ and their product is 1. Find the common ratio and the terms.

Answer:

Given: The sum of the first three terms of a G.P. is $\frac{39}{10}$ and their product is 1.

Let three terms be $\frac{a}{r},a,ar$ .

$S_n=\frac{a(1-r^n)}{1-r}$

$S_3=\frac{a(1-r^3)}{1-r}=\frac{39}{10}$

$\frac{a}{r}+a+ar=\frac{39}{10}.........1$

The product of 3 terms is 1.

$\frac{a}{r}\times a\times ar=1$

$\Rightarrow a^3=1$

$\Rightarrow a=1$

Put the value of an in equation 1,

$\frac{1}{r}+1+r=\frac{39}{10}$

$10(1+r+r^2)=39(r)$

$\Rightarrow 10r^2-29r+10=0$

$\Rightarrow 10r^2-25r-4r+10=0$

$\Rightarrow 5r(2r-5)-2(2r-5)=0$

$\Rightarrow (2r-5)(5r-2)=0$

$\Rightarrow r=\frac{5}{2},r=\frac{2}{5}$

The three terms of AP are $\frac{5}{2},1,\frac{2}{5}$ .

Question 13: How many terms of G.P. $3, 3 ^ 2 3 ^ 3 … are needed to give the sum 120?

Answer:

G.P.= $3 , 3 ^ 2 , 3 ^ 3$ , …............

Sum = 120

These terms are GP with a = 3 and r = 3.

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$120=\frac{3(1-3^n)}{1-3}$

$\Rightarrow$$120\times \frac{-2}{3}=(1-3^n)$

$\Rightarrow$$-80=(1-3^n)$

$\Rightarrow 3^n=1+80=81$

$\Rightarrow 3^n=81$

$\Rightarrow 3^n=3^4$

$\Rightarrow n=4$

Hence, we have a value of n as 4 to get a sum of 120.

Question 14: The sum of the first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio, and the sum to n terms of the G.P.

Answer:

Let GP be $a,ar,ar^2,ar^3,ar^4,ar^5,ar^6................................$

Given: The sum of the first three terms of a G.P. is 16

$a+ar+ar^2=16$

$\Rightarrow a(1+r+r^2)=16...............................(1)$

Given: the sum of the next three terms is 128.

$ar^3+ar^4+ar^5=128$

$\Rightarrow ar^3(1+r+r^2)=128...............................(2)$

Dividing equation (2) by (1), we have

$\Rightarrow \frac{ar^3(1+r+r^2)}{a(1+r+r^2)}=\frac{128}{16}$

$\Rightarrow r^3=8$

$\Rightarrow r^3=2^3$

$\Rightarrow r=2$

Putting the value of r =2 in equation 1, we have

$\Rightarrow a(1+2+2^2)=16$

$\Rightarrow a(7)=16$

$\Rightarrow a=\frac{16}{7}$

$S_n=\frac{a(1-r^n)}{1-r}$

$S_n=\frac{\frac{16}{7}(1-2^n)}{1-2}$

$S_n=\frac{16}{7}(2^n-1)$

Question 15: Given a G.P. with a = 729 and $7 ^{th}$ term 64, determine $s_7$

Answer:

Given a G.P. with a = 729 and $7 ^{th}$ term 64.

$a_n=a.r^{n-1}$

$\Rightarrow 64=729.r^{7-1}$

$\Rightarrow r^6=\frac{64}{729}$

$\Rightarrow r^6=\left ( \frac{2}{3} \right )^6$

$\Rightarrow r=\frac{2}{3}$

$S_n=\frac{a(1-r^n)}{1-r}$

$S_7=\frac{729(1-\left ( \frac{2}{3} \right )^7)}{1-\frac{2}{3}}$

$S_7=\frac{729(1-\left ( \frac{2}{3} \right )^7)}{\frac{1}{3}}$

$S_7=3\times 729 \left ( \frac{3^7-2^7}{3^7} \right )$

$S_7= \left ( 3^7-2^7 \right )$

$S_7= 2187-128$

$S_7= 2059$

Question 16: Find a G.P. for which the sum of the first two terms is – 4 and the fifth term is 4 times the third term

Answer:

Given the sum of the first two terms is – 4 and the fifth term is 4 times the third term

Let the first term be a and the common ratio be r

$a_5=4.a_3$

$\Rightarrow a.r^{5-1}=4.a.r^{3-1}$

$\Rightarrow a.r^{4}=4.a.r^{2}$

$\Rightarrow r^{2}=4$

$\Rightarrow r=\pm 2$

If r = 2, then

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow \frac{a(1-2^2)}{1-2}=-4$

$\Rightarrow \frac{a(1-4)}{-1}=-4$

$\Rightarrow a(-3)=4$

$\Rightarrow a=\frac{-4}{3}$

If r = - 2, then

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow \frac{a(1-(-2)^2)}{1-(-2)}=-4$

$\Rightarrow \frac{a(1-4)}{3}=-4$

$\Rightarrow a(-3)=-12$

$\Rightarrow a=\frac{-12}{-3}=4$

Thus, required GP is $\frac{-4}{3},\frac{-8}{3},\frac{-16}{3},.........$ or $4,-8,-16,-32,..........$.

Question 17: If the $4 ^{th} , 10 ^{th} , 16 ^ {th}$ terms of a G.P. are x, y and z, respectively. Prove that x,y, and z are in G.P.

Answer:

Let x,y, and z be in G.P.

Let first term and common ratio = r

$a_4=a.r^3=x..................(1)$

$a_{10}=a.r^9=y..................(2)$

$a_{16}=a.r^{15}=z..................(3)$

Dividing equation 2 by 1, we have

$\frac{a.r^9}{a.r^3}=\frac{y}{x}$

$\Rightarrow r^4=\frac{y}{x}$

Dividing equation 3 by 2, we have

$\frac{a.r^{15}}{a.r^9}=\frac{z}{y}$

$\Rightarrow r^4=\frac{z}{y}$

Equating values of $r^4$ , we have

$\frac{y}{x}=\frac{z}{y}$

Thus, x, y, z are in GP.

Question 18: Find the sum to n terms of the sequence, 8, 88, 888, 8888….

Answer:

8, 88, 888, 8888… is not a GP.

It can be changed in GP by writing terms such s

$\Rightarrow$$S_n=8+88+888+8888+.............$ to n terms

$\Rightarrow$$S_n=\frac{8}{9}[9+99+999+9999+................]$

$\Rightarrow$$S_n=\frac{8}{9}[(10-1)+(10^2-1)+(10^3-1)+(10^4-1)+................]$

$\Rightarrow$$S_n=\frac{8}{9}[(10+10^2+10^3+........)-(1+1+1.....................)]$

$\Rightarrow$$S_n=\frac{8}{9}[\frac{10(10^n-1)}{10-1}-(n)]$

$\Rightarrow$$S_n=\frac{8}{9}[\frac{10(10^n-1)}{9}-(n)]$

$\Rightarrow$$S_n=\frac{80}{81}(10^n-1)-\frac{8n}{9}$

Question 19: Find the sum of the products of the corresponding terms of the sequences 2, 4, 8, 16, 32 and 128, 32, 8, 2,1/2

Answer:

$Required \, \, sum=2\times 128+4\times 32+8\times 8+16\times 2+32\times \frac{1}{2}$

$Required \, \, sum=64\left [ 4+2+1+\frac{1}{2}+\frac{1}{2^2} \right ]$

Here, $4,2,1,\frac{1}{2},\frac{1}{2^2}$ is a GP.

first term = a = 4

common ratio =r

$r=\frac{1}{2}$

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$S_5=\frac{4(1-\left ( \frac{1}{2} \right )^5)}{1-\frac{1}{2}}$

$\Rightarrow$$S_5=\frac{4(1-\left ( \frac{1}{2} \right )^5)}{\frac{1}{2}}$

$\Rightarrow$$S_5=8(1-\left ( \frac{1}{32} \right ))$

$\Rightarrow$$S_5=8(\frac{31}{32})$

$\Rightarrow$$S_5=\frac{31}{4}$

$Required \, \, sum=64\left [ \frac{31}{4} \right ]$

$Required \, \, sum=16\times 31=496$

Question 20: Show that the products of the corresponding terms of the sequences $a, ar, ar^, ...ar^{n-1} \: \: and\: \: A, A R, AR^2 ....AR^{n-1}$ form a G.P, and find the common ratio.

Answer:

To prove : $aA,arAR,ar^2AR^2,...................$ is a GP.

$\frac{second \, \, term}{first\, \, term}=\frac{arAR}{aA}=rR$

$\frac{third \, \, term}{second\, \, term}=\frac{ar^2AR^2}{arAR}=rR$

Thus, the above sequence is a GP with a common ratio of rR.

Question 21: Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the $4 ^{th}$ by 18.

Answer:

Let the first term be a and the common ratio be r.

$a_1=a,a_2=ar,a_3=ar^2,a_4=ar^3$

Given: the third term is greater than the first term by 9, and the second term is greater than the $4 ^{th}$ by 18.

$a_3=a_1+9$

$\Rightarrow ar^2=a+9$

$\Rightarrow a(r^2-1)=9.................1$

$a_2=a_4+18$

$\Rightarrow ar=ar^3+18$

$\Rightarrow ar(1-r^2)=18......................2$

By dividing equation 2 by 1 we get

$\frac{ ar(1-r^2)}{ -a(1-r^2)}=\frac{18}{9}$

$\Rightarrow r=-2$

Putting the value of r, we get

$4a=a+9$

$\Rightarrow 4a-a=9$

$\Rightarrow 3a=9$

$\Rightarrow a=3$

Thus, four terms of GP are $3,-6,12,-24.$

Question 22: If the $p^{th} q ^{th},r ^{th}$ terms of a G.P. are a, b and c, respectively. Prove that $a ^{ q-r } b ^{r- p } C ^{p-q} = 1$

Answer:

To prove : $a ^{ q-r } b ^{r- p } C ^{p-q} = 1$

Let A be the first term and R be the common ratio.

According to the given information, we have

$a_p=A.R^{p-1}=a$

$a_q=A.R^{q-1}=b$

$a_r=A.R^{r-1}=c$

L.H.S : $a ^{ q-r } b ^{r- p } C ^{p-q}$

$\Rightarrow$$A^{q-r}.R^{(q-r)(p-1)}.A^{r-p}.R^{(r-p)(q-1)}.A^{p-q}.R^{(p-q)(r-1)}$

$\Rightarrow$$A^{q-r+r-p+p-q}.R^{(qp-rp-q+r)+(rq-pq+p-r)+(pr-p-qr+q)}$

$\Rightarrow$$A^0.R^0=1$ =RHS

Thus, LHS = RHS.

Hence proved.

Question 23: If the first and the nth terms of a G.P. are a and b, respectively, and if P is the product of n terms, prove that $P^2 = ( ab)^n.

Answer:

Given First term =a and n th term = b.

Common ratio = r.

To prove : $P^2 = ( ab)^n$

Then , $GP = a,ar,ar^2,ar^3,ar^4,..........................$

$a_n=a.r^{n-1}=b..................................1$

P = product of n terms

$\Rightarrow$$P=(a).(ar).(ar^2).(ar^3)..............(ar^{n-1})$

$\Rightarrow$$P=(a.a.a...............a)((1).(r).(r^2).(r^3)..............(r^{n-1}))$

$\Rightarrow$$P=(a^n)(r^{1+2+.........(n-1)})........................................2$

Here, $1+2+.........(n-1)$ is aananP.

$\therefore\, \, \, sum= \frac{n}{2}\left [2a+(n-1)d \right ]$

$\Rightarrow$$ \frac{n-1}{2}\left [2(1)+(n-1-1)1 \right ]$

$\Rightarrow$$ \frac{n-1}{2}\left [2+n-2 \right ]$

$\Rightarrow$$ \frac{n-1}{2}\left [n \right ]$

$\Rightarrow$$ \frac{n(n-1)}{2}$

Put in equation (2),

$P=(a^n)(r^{\frac{n(n-1)}{2}})$

$\Rightarrow$$P^2=(a^{2n})(r^{n(n-1)})$

$\Rightarrow$$P^2=(a. a.r^{(n-1)})^n$

$\Rightarrow$$P^2=(a.b)^n$

Hence proved.

Question 24: Show that the ratio of the sum of the first n terms of a G.P. to the sum of terms from $( n+1)^{th} \: \: to\: \: (2n)^{th}$ term is $\frac{1}{r^n}$

Answer:

Let the first term =a and common ratio = r.

$sum \, \, of\, \, n\, \, terms=\frac{a(1-r^n)}{1-r}$

Since there are n terms from (n+1) to 2n term.

The sum of terms from (n+1) to 2n.

$S_n=\frac{a_{(n+1)}(1-r^n)}{1-r}$

$a_{(n+1)}=a.r^{n+1-1}=ar^n$

Thus, the required ratio = $\frac{a(1-r^n)}{1-r}\times \frac{1-r}{ar^n(1-r^n)}$

$=\frac{1}{r^n}$

Thus, the common ratio of the sum of the first n terms of a G.P. to the sum of terms from $( n+1)^{th} \: \: to\: \: (2n)^{th}$ term is $\frac{1}{r^n}$.

Question 25: If a, b, c, and d are in G.P. show that $(a^2 + b^2 + c^2) (b^2 + c^2 + d^2) = (ab + bc + cd)^2 .$

Answer:

If a, b, c, and d are in G.P.

$bc=ad....................(1)$

$b^2=ac....................(2)$

$c^2=bd....................(3)$

To prove : $(a^2 + b^2 + c^2) (b^2 + c^2 + d^2) = (ab + bc + cd)^2 .$

RHS : $(ab + bc + cd)^2 .$

$\Rightarrow$$(ab + ad + cd)^2 .$

$\Rightarrow$$(ab + d (a+ c))^2 .$

$\Rightarrow$$a^2b^2 + d^2 (a+ c)^2 + 2(ab)(d(a+c))$

$\Rightarrow$$a^2b^2 + d^2 (a^2+ c^2+2ac) + 2a^2bd+2bcd$

Using equation (1) and (2),

$\Rightarrow$$a^2b^2 + 2a^2c^2+ 2b^2c^2+d^2a^2+2d^2b^2+d^2c^2$

$\Rightarrow$$a^2b^2 + a^2c^2+ a^2c^2+b^2c^2+b^2c^2+d^2a^2+d^2b^2+d^2b^2+d^2c^2$

$\Rightarrow$$a^2b^2 + a^2c^2+ a^2d^2+b^2.b^2+b^2c^2+b^2d^2+c^2b^2+c^2.c^2+d^2c^2$

$\Rightarrow$$a^2(b^2 + c^2+ d^2)+b^2(b^2+c^2+d^2)+c^2(b^2+c^2+d^2)$

$\Rightarrow$$(b^2 + c^2+ d^2)(a^2+b^2+c^2)$ = LHS

Hence proved.

Question 26: Insert two numbers between 3 and 81 so that the resulting sequence is G.P.

Answer:

Let A, and B be two numbers between 3 and 81 such that series 3, A, B, and 81 form a GP.

Let a=first term and common ratio =r.

$\therefore a_4=a.r^{4-1}$

$\Rightarrow$$81=3.r^{3}$

$\Rightarrow$$27=r^{3}$

$\Rightarrow$$r=3$

For $r=3$ ,

$A=ar=(3)(3)=9$

$B=ar^2=(3)(3)^2=27$

The required numbers are 9,27.

Question 27: Find the value of n so that $\frac{a^{n+1}+ b ^{n+1}}{a^n+b^n}$ may be the geometric mean between a and b.

Answer:

M of a and b is $\sqrt{ab}.$

Given :

$\frac{a^{n+1}+ b ^{n+1}}{a^n+b^n}=\sqrt{ab}$

Squaring both sides

$\left ( \frac{a^{n+1}+ b ^{n+1}}{a^n+b^n} \right )^2=ab$

$\left (a^{n+1}+ b ^{n+1})^2=({a^n+b^n} \right )^2ab$

$\Rightarrow \left (a^{2n+2}+ b ^{2n+2}+2.a^{n+1}.b^{n+1})=({a^{2n}+b^{2n}+2.a^n.b^n} \right )ab$

$\Rightarrow \left (a^{2n+2}+ b ^{2n+2}+2.a^{n+1}.b^{n+1})=({a^{2n+1}.b+a.b^{2n+1}+2.a^{n+1}.b^{n+1}} \right )$

$\Rightarrow \left (a^{2n+2}+ b ^{2n+2})=({a^{2n+1}.b+a.b^{2n+1}} \right )$

$\Rightarrow a^{2n+1}(a-b)=b^{2n+1}( a-b)$

$\Rightarrow a^{2n+1}=b^{2n+1}$

$\Rightarrow \left ( \frac{a}{b} \right )^{2n+1}=1$

$\Rightarrow \left ( \frac{a}{b} \right )^{2n+1}=1=\left ( \frac{a}{b} \right )^0$

$\Rightarrow 2n+1=0$

$\Rightarrow 2n=-1$

$\Rightarrow n=\frac{-1}{2}$

Question 28: The sum of two numbers is 6 times their geometric mean, showing numbers are in the ratio $( 3+ 2 \sqrt 2 ) : ( 3 - 2 \sqrt 2 )$

Answer:

Let there be two numbers a and b

Geometric mean $=\sqrt{ab}$

According to the given condition,

$a+b=6\sqrt{ab}$

$\Rightarrow$$(a+b)^2=36(ab)$ .............................................................(1)

Also, $(a-b)^2=(a+b)^2-4ab=36ab-4ab=32ab$

$(a-b)=\sqrt{32}\sqrt{ab}$

$\Rightarrow$$(a-b)=4\sqrt{2}\sqrt{ab}$ .......................................................(2)

From (1) and (2), we get

$2a=(6+4\sqrt{2})\sqrt{ab}$

$\Rightarrow$$a=(3+2\sqrt{2})\sqrt{ab}$

Putting the value of 'a' in (1),

$\Rightarrow$$b=6\sqrt{ab}-(3+2\sqrt{2})\sqrt{ab}$

$\Rightarrow$$b=(3-2\sqrt{2})\sqrt{ab}$

$\Rightarrow$$\frac{a}{b}=\frac{(3+2\sqrt{2})\sqrt{ab}}{(3-2\sqrt{2})\sqrt{ab}}$

$\Rightarrow$$\frac{a}{b}=\frac{(3+2\sqrt{2})}{(3-2\sqrt{2})}$

Thus, the ratio is $( 3+ 2 \sqrt 2 ) : ( 3 - 2 \sqrt 2 )$.

Question 29: If A and G are A.M. and G.M., respectively between two positive numbers, prove that the numbers are $A \pm \sqrt{( A+G)(A-G)}$

Answer:

If A and Garee A.M. and G.M., respectively between two positive numbers,
Two numberarebe a and b.

$AM=A=\frac{a+b}{2}$

$\Rightarrow a+b=2A$ ...................................................................1

$GM=G=\sqrt{ab}$

$\Rightarrow ab=G^2$ ...........................................................................2

We know $(a-b)^2=(a+b)^2-4ab$

Put values from equation 1 and 2,

$(a-b)^2=4A^2-4G^2$

$\Rightarrow$$(a-b)^2=4(A^2-G^2)$

$\Rightarrow$$(a-b)^2=4(A+G)(A-G)$

$\Rightarrow$$(a-b)=4\sqrt{(A+G)(A-G)}$ ..................................................................3

From 1 and 3, we have

$2a=2A+2\sqrt{(A+G)(A-G)}$

$\Rightarrow a=A+\sqrt{(A+G)(A-G)}$

Put the value of an in equation 1, and we get

$b=2A-A-\sqrt{(A+G)(A-G)}$

$\Rightarrow b=A-\sqrt{(A+G)(A-G)}$

Thus, numbers are $A \pm \sqrt{( A+G)(A-G)}$.

Question 30: The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of the 2nd hour, 4th hour, and nth hour?

Answer:

The number of bacteria in a certain culture doubles every hour. It forms GP.

Given a = 30 and r = 2.

$a_3=a.r^{3-1}=30(2)^2=120$

$a_5=a.r^{5-1}=30(2)^4=480$

$a_n+_1=a.r^{n+1-1}=30(2)^n$

Thus, bacteria present at the end of the 2nd hour, 4th hour, r, and nth hour are 120,480 and $30(2)^n$ respectively.

Question 31: What will R50 amount to in 10 years after its deposit in a bank that pays an annual interest rate of 10% compounded annually?

Answer:

Given: The Bank pays an annual interest rate of 10% compounded annually.

Rs 500 amounts are deposited in the bank.

At the end of the first year, the amount

$=500\left ( 1+\frac{1}{10} \right )=500(1.1)$

At the end of the second year, the amount $=500(1.1)(1.1)$

At the end of the third year, the amount $=500(1.1)(1.1)(1.1)$

At the end of 10 years, the amount $=500(1.1)(1.1)(1.1)........(10times)$

$=500(1.1)^{10}$

Thus, at the end of 10 years, amount $=Rs. 500(1.1)^{10}$.

Question 32: If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation

Answer:

Let the roots of the quadratic equation be a and b.

According to the given conditions,

$AM=\frac{a+b}{2}=8$

$\Rightarrow (a+b)=16$

$GM=\sqrt{ab}=5$

$\Rightarrow ab=25$

We know that $x^2-x(sum\, of\, roots)+(product\, of\, roots)=0$

$\Rightarrow$$x^2-x(16)+(25)=0$

$\Rightarrow$$x^2-16x+25=0$

Thus, the quadratic equation = $x^2-16x+25=0$

Question 1: If f is a function satisfying f (x +y) = f(x) f(y) for all x, y $\epsilon$ N such that f(1) = 3 and

$\sum_{x=1}^{n} f(x) = 120$ , find the value of n.

Answer:

Given : f (x +y) = f(x) f(y) for all x, y $\epsilon$ N such that f(1) = 3

$f(1) = 3$

Taking $x=y=1$ , we have

$f(1+1)=f(2)=f(1)*f(1)=3*3=9$

$\Rightarrow f(1+1+1)=f(1+2)=f(1)*f(2)=3*9=27$

$\Rightarrow f(1+1+1+1)=f(1+3)=f(1)*f(3)=3*27=81$

$f(1),f(2),f(3),f(4).....................$ is $3,9,27,81,..............................$ forms a GP with first term=3 and common ratio = 3.

$\sum_{x=1}^{n} f(x) = 120=S_n$

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$120=\frac{3(1-3^n)}{1-3}$

$\Rightarrow$$40=\frac{(1-3^n)}{-2}$

$\Rightarrow$$-80=(1-3^n)$

$\Rightarrow$$-80-1=(-3^n)$

$\Rightarrow$$-81=(-3^n)$

$\Rightarrow$$3^n=81$

Therefore, $n=4$

Thus, the value of n is 4.

Question 2: The sum of some terms of G.P. is 315 whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms.

Answer:

Let the sum of some terms of G.P. is 315 whose first term and the common ratio are 5 and 2

$S_n=\frac{a(1-r^n)}{1-r}$

$\Rightarrow$$315=\frac{5(1-2^n)}{1-2}$

$\Rightarrow$$63=\frac{(1-2^n)}{-1}$

$\Rightarrow$$-63=(1-2^n)$

$\Rightarrow$$-63-1=(-2^n)$

$\Rightarrow$$-64=(-2^n)$

$\Rightarrow$$2^n=64$

Therefore, $n=6$

Thus, the value of n is 6.

Last term of GP = 6th term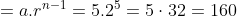

The last term of GP =160

Question 3: The first term of a G.P. is 1. The sum of the third term and fifth term is 90. Find the common ratio of G.P.

Answer:

Given: The first term of a G.P. is 1. The sum of the third term and fifth term is 90.

$a=1$

$a_3=a.r^2=r^2$ $a_5=a.r^4=r^4$

$\therefore \, \, r^2+r^4=90$

$\therefore \, \, r^4+r^2-90=0$

$\Rightarrow \, \, r^2=\frac{-1\pm \sqrt{1+360}}{2}$

$\Rightarrow$$r^2=\frac{-1\pm \sqrt{361}}{2}$

$\Rightarrow$$r^2=-10 \, or \, 9$

$\Rightarrow$$r=\pm 3$

Thus, the common ratio of GP is $\pm 3$.

Question 4: The sum of three numbers in G.P. is 56. If we subtract 1, 7, 2and 1 from these numbers in that order, we obtain an arithmetic progression. Find the numbers.

Answer:

Let three terms of GP be $a, ar,ar^2.$

Then, we have $a+ar+ar^2=56$

$a(1+r+r^2)=56$ ...............................................1

$a-1,ar-7,ar^2-21$ from an AP.

$\therefore ar-7-(a-1)=ar^2-21-(ar-7)$

$ar-7-a+1=ar^2-21-ar+7$

$ar-6-a=ar^2-14-ar$

$\Rightarrow ar^2-2ar+a=8$

$\Rightarrow ar^2-ar-ar+a=8$
$\Rightarrow a(r^2-2r+1)=8$

$\Rightarrow a(r^2-1)^2=8$ ....................................................................2

From equation 1 and 2, we get

$\Rightarrow 7(r^2-2r+1)=1+r+r^2$

$\Rightarrow 7r^2-14r+7-1-r-r^2=0$

$\Rightarrow 6r^2-15r+6=0$

$\Rightarrow 2r^2-5r+2=0$

$\Rightarrow 2r^2-4r-r+2=0$

$\Rightarrow 2r(r-2)-1(r-2)=0$

$\Rightarrow (r-2)(2r-1)=0$

$\Rightarrow r=2,r=\frac{1}{2}$

If r = 2, GP = 8,16,32

If r=0.2, GP= 32,16,8.

Thus, the numbers required are 8,16,32.

Question 5: A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.

Answer:

Let GP be $A_1,A_2,A_3,...................A_{2n}$

Number of terms = 2n

According to the given condition,

Lettheme be GP as $a,ar,ar^2,..................$

$\Rightarrow \frac{ar(r^n-1)}{r-1}=\frac{4.a(r^{n}-1)}{r-1}$

$\Rightarrow ar=4a$

$\Rightarrow r=4$

Thus, the common ratio is 4.

Question 6: If $\frac{a+ bx}{a-bx} = \frac{b+cx}{b-cx} = \frac{c+dx}{c-dx} (x\neq 0 )$ then show that a, b, c and d are in G.P.

Answer:

Given :

$\frac{a+ bx}{a-bx} = \frac{b+cx}{b-cx} = \frac{c+dx}{c-dx} (x\neq 0 )$

Takin,

$\frac{a+ bx}{a-bx} = \frac{b+cx}{b-cx}$

$\Rightarrow (a+ bx) (b-cx) = (b+cx) (a-bx)$

$\Rightarrow ab+ b^2x-bcx^2-acx) = ba-b^2x+acx-bcx^2$

$\Rightarrow 2 b^2x = 2acx$

$\Rightarrow b^2 = ac$

$\Rightarrow \frac{b}{a}=\frac{c}{b}..................1$

Taking,

$\frac{b+cx}{b-cx} = \frac{c+dx}{c-dx}$

$\Rightarrow (b+cx)(c-dx)=(c+dx)(b-cx)$

$\Rightarrow bc-bdx+c^2x-cdx^2=bc-c^2x+bdx-cdx^2$

$\Rightarrow 2bdx=2c^2x$

$\Rightarrow bd=c^2$

$\Rightarrow \frac{d}{c}=\frac{c}{b}..............................2$

From equation 1 and 2, we have

$\Rightarrow \frac{d}{c}=\frac{c}{b}=\frac{b}{a}$

Thus, a,b,c,d and are in GP.

Question 7: Let S be the sum, P the product, and R the sum of reciprocals of n terms in a G.P. Prove that $P^2 R^n = S ^n$

Answer:

Let there be a GP $=a,ar,ar^2,ar^3,....................$

According to the given information,

$S=\frac{a(r^n-1)}{r-1}$

$P=a^n \times r^{(1+2+...................n-1)}$

$\Rightarrow P=a^n \times r^{\frac{n(n-1)}{2}}$

$R=\frac{1}{a}+\frac{1}{ar}+\frac{1}{ar^2}+..................\frac{1}{ar^{n-1}}$

$\Rightarrow R=\frac{r^{n-1}+r^{n-2}+r^{n-3}+..............r+1}{a.r^{n-1}}$

$\Rightarrow R=\frac{1}{a.r^{n-1}}\times \frac{1(r^n-1)}{r-1}$

$\Rightarrow R= \frac{(r^n-1)}{a.r^{n-1}.(r-1)}$

To prove : $P^2 R^n = S ^n$

LHS : $P^2 R^n$

$= a^{2n}.r^{n(n-1)}\frac{(r^n-1)^n}{a^n.r^{n(n-1)}.(r-1)^n}$

$= a^{n} \frac{(r^n-1)^n}{(r-1)^n}$

$= \left ( \frac{a(r^n-1)}{(r-1)} \right )^{n}$

$=S^n=RHS$

Hence proved.

Question 8: If a, b, c, d are in G.P, prove that $(a^n + b^n), (b^n + c^n), (c^n + d^n)$ are in G.P.

Answer:

Given: a, b, c, d are in G.P.

To prove: $(a^n + b^n), (b^n + c^n), (c^n + d^n)$ are in G.P.

Then we can write,

$b^2=ac...............................1$

$c^2=bd...............................2$

$ad=bc...............................3$

Let $(a^n + b^n), (b^n + c^n), (c^n + d^n)$ be in GP.

$(b^n + c^n)^2 =(a^n + b^n) (c^n + d^n)$

LHS: $(b^n + c^n)^2$

$(b^n + c^n)^2 =b^{2n}+c^{2n}+2b^nc^n$

$(b^n + c^n)^2 =(b^2)^n+(c^2)^n+2b^nc^n$

$=(ac)^n+(bd)^n+2b^nc^n$

$=a^nc^n+b^nc^n+a^nd^n+b^nd^n$

$=c^n(a^n+b^n)+d^n(a^n+b^n)$

$=(a^n+b^n)(c^n+d^n)=RHS$

Hence proved.

Thus, $(a^n + b^n), (b^n + c^n), (c^n + d^n)$ are in GP

Question 9: If a and b are the roots of $x^2 -3 x + p = 0$ and c, d are roots of $x^2 -12 x + q = 0$, where a, b, c, d form a G.P. Prove that (q + p) : (q – p) = 17:15.

Answer:

Given: a and b are the roots of $x^2 -3 x + p = 0$

Then, $a+b=3\, \, \, \, and\, \, \, \, ab=p......................1$

Also, c, d are roots of $x^2 -12 x + q = 0$

$c+d=12\, \, \, \, and\, \, \, \, cd=q......................2$

Given: a, b, c, d form a G.P

Let, $a=x,b=xr,c=xr^2,d=xr^3$

From 1 and 2, we get

$x+xr=3$ and $xr^2+xr^3=12$

$\Rightarrow x(1+r)=3$ $xr^2(1+r)=12$

On dividing them,

$\frac{xr^2(1+r)}{x(1+r)}=\frac{12}{3}$

$\Rightarrow r^2=4$

$\Rightarrow r=\pm 2$

When , r = 2,

$x=\frac{3}{1+2}=1$

When, r = -2,

$x=\frac{3}{1-2}=-3$

Case (1) when r=2 and x=1,

$ab=x^2r=2\, \, \, and \, \, \, \, cd=x^2r^5=32$

$\therefore \frac{q+p}{q-p}=\frac{32+2}{32-2}=\frac{34}{30}=\frac{17}{15}$

i.e. (q + p) : (q – p) = 17:15.

Case (2) when r = -2 and x = -3,

$ab=x^2r=-18\, \, \, and \, \, \, \, cd=x^2r^5=-288$

$\therefore \frac{q+p}{q-p}=\frac{-288-18}{-288+18}=\frac{-305}{-270}=\frac{17}{15}$

i.e. (q + p) : (q – p) = 17 : 15.

Question 10: The ratio of the A.M. and G.M. of two positive numbers a and b, is m n. Show that $a: b = \left ( m + \sqrt {m^2 -n^2 }\right ) : \left ( m- \sqrt {m^2 - n^2} \right )$

Answer:

Let two numbers be a and b.

$AM=\frac{a+b}{2}\, \, \, and\, \, \, \, \, GM=\sqrt{ab}$

According to the given condition,

$\frac{a+b}{2\sqrt{ab}}=\frac{m}{n}$

$\Rightarrow \frac{(a+b)^2}{4ab}=\frac{m^2}{n^2}$

$\Rightarrow (a+b)^2=\frac{4ab.m^2}{n^2}$

$\Rightarrow (a+b)=\frac{2\sqrt{ab}.m}{n}$ ...................................................................1

$(a-b)^2=(a+b)^2-4ab$

We get,

$(a-b)^2=\left ( \frac{4abm^2}{n^2} \right )-4ab$

$(a-b)^2=\left ( \frac{4abm^2-4abn^2}{n^2} \right )$

$\Rightarrow (a-b)^2=\left ( \frac{4ab(m^2-n^2)}{n^2} \right )$

$\Rightarrow (a-b)=\left ( \frac{2\sqrt{ab}\sqrt{(m^2-n^2)}}{n} \right )$ .....................................................2

From 1 and 2, we get

$2a =\left ( \frac{2\sqrt{ab}}{n} \right )\left ( m+\sqrt{(m^2-n^2)} \right )$

$\Rightarrow a =\left ( \frac{\sqrt{ab}}{n} \right )\left ( m+\sqrt{(m^2-n^2)} \right )$

Putting the value of an ann equation 1, we have

$b=\left ( \frac{2.\sqrt{ab}}{n} \right ) m-\left ( \frac{\sqrt{ab}}{n} \right )\left ( m+\sqrt{(m^2-n^2)} \right )$

$\Rightarrow b=\left ( \frac{\sqrt{ab}}{n} \right ) m-\left ( \frac{\sqrt{ab}}{n} \right )\left ( \sqrt{(m^2-n^2)} \right )$

$=\left ( \frac{\sqrt{ab}}{n} \right )\left (m- \sqrt{(m^2-n^2)} \right )$

$\therefore a:b=\frac{a}{b}=\frac{\left ( \frac{\sqrt{ab}}{n} \right )\left (m+ \sqrt{(m^2-n^2)} \right )}{\left ( \frac{\sqrt{ab}}{n} \right )\left (m- \sqrt{(m^2-n^2)} \right )}$

$=\frac{\left (m+ \sqrt{(m^2-n^2)} \right )}{\left (m- \sqrt{(m^2-n^2)} \right )}$

$a:b=\left (m+ \sqrt{(m^2-n^2)} \right ) : \left (m- \sqrt{(m^2-n^2)} \right )$

Question 11: Find the sum of the following series up to n terms:

(i) $5 + 55+ 555 + ....$

(ii) .6 +. 66 +. 666+…

Answer:

(i) $5 + 55+ 555 + ....$ is not a GP.

It can be changed in GP by writing terms such s

$S_n=5 + 55+ 555 + ....$ to n terms

$S_n=\frac{5}{9}[9+99+999+9999+................]$

$S_n=\frac{5}{9}[(10-1)+(10^2-1)+(10^3-1)+(10^4-1)+................]$

$S_n=\frac{5}{9}[(10+10^2+10^3+........)-(1+1+1.....................)]$

$S_n=\frac{5}{9}[\frac{10(10^n-1)}{10-1}-(n)]$

$S_n=\frac{5}{9}[\frac{10(10^n-1)}{9}-(n)]$

$S_n=\frac{50}{81}[(10^n-1)]-\frac{5n}{9}$

Thus, the sum is

$S_n=\frac{50}{81}[(10^n-1)]-\frac{5n}{9}$

(ii) The sum of 0.6 +0. 66 + 0. 666+….................

It can be written as

$S_n=0.6+0.66+0.666+..........................$ to n terms

$\Rightarrow S_n=6[0.1+0.11+0.111+0.1111+................]$

$\Rightarrow S_n=\frac{6}{9}[0.9+0.99+0.999+0.9999+................]$

$\Rightarrow S_n=\frac{6}{9}[(1-\frac{1}{10})+(1-\frac{1}{10^2})+(1-\frac{1}{10^3})+(1-\frac{1}{10^4})+................]$

$\Rightarrow S_n=\frac{2}{3}[(1+1+1.....................n\, terms)-\frac{1}{10}(1+\frac{1}{10}+\frac{1}{10^2}+...................n \, terms)]$

$\Rightarrow S_n=\frac{2}{3}[n-\frac{\frac{1}{10}(\frac{1}{10}^n-1)}{\frac{1}{10}-1}]$

$\Rightarrow S_n=\frac{2n}{3}-\frac{2}{30}[\frac{10(1-10^{-n})}{9}]$

$\Rightarrow S_n=\frac{2n}{3}-\frac{2}{27}(1-10^{-n})$

Question 12: Find the 20th term of the series $2 \times 4+4\times 6+\times 6\times 8+....+n$ terms.

Answer:

The series = $2 \times 4+4\times 6+\times 6\times 8+....+n$

$\therefore n^{th}\, term=a_n=2n(2n+2)=4n^2+4n$

$\therefore a_{20}=2(20)[2(20)+2]$

$=40[40+2]$

$=40[42]$

$=1680$

Thus, the 20th term of the series is 1680

Question 13: A farmer buys a used tractor for Rs 12000. He pays Rs 6000 cash and agrees to pay the balance in annual installments of Rs 500 plus 12% interest on the unpaid amount. How much will the tractor cost him?

Answer:

Given Farmer pays Rs 6000 cash.

Therefore, unpaid amount = 12000-6000=Rs. 6000

According to the condition, interest paid annually is

12% of 6000,12% of 5500,12% of 5000,......................12% of 500.

Thus, the total interest to be paid

$=12\%of\, 6000+12\%of\, 5500+.............12\%of\, 500$

$=12\%of\, (6000+ 5500+.............+ 500)$

$=12\%of\, (500+ 1000+.............+ 6000)$

Here, $500, 1000,.............5500,6000$ is a AP with first term =a=500 and common difference =d = 500

We know that $a_n=a+(n-1)d$

$\Rightarrow 6000=500+(n-1)500$

$\Rightarrow 5500=(n-1)500$

$\Rightarrow 11=(n-1)$

$\Rightarrow n=11+1=12$

The sum of AP:

$S_{12}=\frac{12}{2}\left [ 2(500)+(12-1)500 \right ]$

$\Rightarrow S_{12}=6\left [ 1000+5500 \right ]$

$=6\left [ 6500 \right ]$

$=39000$

Thus, interest to be paid :

$=12\%of\, (500+ 1000+.............+ 6000)$

$=12\%of\, ( 39000)$

$=Rs. 4680$

Thus, cost of tractor = Rs. 12000+ Rs. 4680 = Rs. 16680

Question 14: Shamshad Ali buys a scooter for Rs 22000. He pays Rs 4000 cash and agrees to pay the balance in an annual installment of Rs 1000 plus 10% interest on the unpaid amount. How much will the scooter cost him?

Answer:

Given: Shamshad Ali buys a scooter for Rs 22000.

Therefore, the unpaid amount = 22000-4000=Rs. 18000

According to the given condition, interest paid annually is

10% of 18000,10% of 17000,10% of 16000,......................10% of 1000.

Thus, the total interest to be paid

$=10\%of\, 18000+10\%of\, 17000+.............10\%of\, 1000$

$=10\%of\, (18000+ 17000+.............+ 1000)$

$=10\%of\, (1000+ 2000+.............+ 18000)$

Here, $1000, 2000,.............17000,18000$ is a AP with first term =a=1000 and common difference =d = 1000

We know that $a_n=a+(n-1)d$

$\Rightarrow 18000=1000+(n-1)1000$

$\Rightarrow 17000=(n-1)1000$

$\Rightarrow 17=(n-1)$

$\Rightarrow n=17+1=18$

The sum of AP:

$S_{18}=\frac{18}{2}\left [ 2(1000)+(18-1)1000 \right ]$

$=9\left [ 2000+17000 \right ]$

$=9\left [ 19000 \right ]$

$=171000$

Thus, interest to be paid :

$=10\%of\, (1000+ 2000+.............+ 18000)$

$=10\%of\, ( 171000)$

$=Rs. 17100$

Thus, cost of tractor = Rs. 22000 + Rs. 17100 = Rs. 39100

Question 15: A person writes a letter to four of his friends. He asks each one of them to copy the letter and mail it to four different persons with the instruction that they move the chain similarly. Assuming that the chain is not broken and that it costs 50 paise to mail one letter. Find the amount spent on the postage when the 8th set of letters is mailed.

Answer:

The number of letters mailed from a GP: $4,4^2,4^3,.............4^8$

First term = a=4

Common ratio=r=4

Number of terms = 8

We know that the sum of GP is

$S_n=\frac{a(r^n-1)}{r-1}$

$=\frac{4(4^8-1)}{4-1}$

$=\frac{4(65536-1)}{3}$

$=\frac{4(65535)}{3}$

$=87380$

Costs to mail one letter are 50 paise.

Cost of mailing 87380 letters

$=Rs. \, 87380\times \frac{50}{100}$

$=Rs. \,43690$

Thus, the amount spent when the 8th set of the letter is mailed is Rs. 43690.

Question 16: A man deposited Rs 10000 in a bank at the rate of 5% simple interest annually. Find the amount in 1the 5th year since he deposited the amount and also calculate the total amount after 20 years.

Answer:

Given: A man deposited Rs 10000 in a bank at the rate of 5% simple interest annually.

$=\frac{5}{100}\times 10000=Rs.500$

$\therefore$ Interest in fifteen year 10000+ 14 times Rs. 500

$\therefore$ Amount in 15 th year $=Rs. 10000+14\times 500$

$=Rs. 10000+7000$

$=Rs. 17000$

$\therefore$ Amount in 20 th year $=Rs. 10000+20\times 500$

$=Rs. 10000+10000$

$=Rs. 20000$

Question 17: A manufacturer reckons that the value of a machine, which costs him Rs. 15625, will depreciate each year by 20%. Find the estimated value at the end of 5 years.

Answer:

Cost of machine = Rs. 15625

Machines depreciate each year by 20%.

Therefore, its value every year is 80% of the original cost i.e. $\frac{4}{5}$ of the original cost.

$\therefore$ Value at the end of 5 years

$=15625\times \frac{4}{5}\times \frac{4}{5}\times \frac{4}{5}\times \frac{4}{5}\times \frac{4}{5}$

$=5120$

Thus, the value of the machine at the end of 5 years is Rs. 5120

Question 18: 150 workers were engaged to finish a job in a certain number of days. 4 workers dropped out on the second day, 4 more workers dropped out on the third day, and so on.

Answer:

Let x be the number of days in which 150 workers finish the work.

According to the given information, we have

$150x=150+146+142+............(x+8)terms$

Series $150x=150+146+142+............(x+8)terms$ is a AP

First term=a=150

Common difference= -4

Number of terms = x+8

$\Rightarrow 150x=\frac{x+8}{2}\left [ 2(150)+(x+8-1)(-4) \right ]$

$\Rightarrow 300x=x+8\left [ 300-4x-28 \right ]$

$\Rightarrow 300x= 300x-4x^2-28x+2400-32x+224$

$\Rightarrow x^2+15x-544=0$

$\Rightarrow x^2+32x-17x-544=0$

$\Rightarrow x(x+32)-17(x+32)=0$

$\Rightarrow (x+32)(x-17)=0$

$\Rightarrow x=-32,17$

Since x cannot be negative so x=17.

Thus, in 17 days 150 workers finish the work.

Thus, the required number of days = 17+8=25 days.