Introduction To Three Dimensional Geometry Class 11th Notes - Free NCERT Class 11 Maths Chapter 12 notes - Download PDF

Introduction to Three-Dimensional Geometry Class 11 Notes PDF download: Free PDF Download

Students who wish to access the Introduction to Three-Dimensional Geometry Class 11 Maths notes can click on the link below to download the entire notes in PDF.

Download PDF

Introduction To Three Dimensional Geometry Class 11 Notes

Careers360 has prepared these Class 11 Introduction to Three Dimensional Geometry Notes to make your revision smoother and faster.

Distance Formula

Suppose that there are two points $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ then the distance formula is given as

$d=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2+\left(z_1-z_2\right)^2}$

Section Formula

Suppose that there are two points $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ are divided into $m:n$.

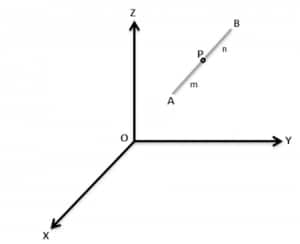
The section formula is given as:

$\left(x^{\prime}, y^{\prime}, z^{\prime}\right)=\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}, \frac{m z_2+n z_1}{m+n}\right)$

System Of Planes

An equation of a plane contains three independent constants; as such, a plane is uniquely determined by three independent conditions. If we consider a plane satisfying just two given conditions, its equation will contain one arbitrary constant. If we consider a plane satisfying one given condition, its equation will contain two arbitrary constants.

We give below the equations of some well-known systems of planes:

The equation $ax + by + cz + k = 0$ represents a system of planes parallel to the plane $ax + by + cz + d = 0$,
where $d$ and $k$ are parameters.

The equation $ax + by + cz + k = 0$ represents a system of planes perpendicular to the line $\frac{x}{a} = \frac{y}{b} = \frac{z}{c}$.

The equation $a_1x + b_1y + c_1z + d_1 + λ(a_2x + b_2y + c_2z + d_2)= 0$ is a system of planes passing through the intersection of the planes
$a_1x + b_1y + c_1z + d_1 = 0$ and $a_2x + b_2y + c_2z + d_2 = 0$,
where $λ$ is a parameter.

Angle Between Two Planes

Let there be two planes
$a_1x + b_1y + c_1z + d_1 = 0$ and $a_2x + b_2y + c_2z + d_2 = 0$

Then the angle between is given as

$\cos\theta=\left|\frac{a_1a_2+b_1b_2+c_1c_2}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\right|$

The Symmetrical Form Of The Equation Of A Line

If a straight line passes through a given point $(x_1,y_1,z_1)$ and has direction cosines $l, m, n,$ then the coordinates of any point on it satisfy the equations

$\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$

Vector Equations

The parametric vector equation of the line through a point with position vector $a$ and parallel to the vector $b$ is:
$\vec{r}=\overrightarrow{\mathrm{a}}+\lambda \vec{b}$, where $λ$ is a scalar parameter.

Introduction to Three Dimensional Geometry: Previous Year Question and Answer

Given below are selected previous year question answers for NCERT Class 11 Maths Chapter 11 Introduction to Three Dimensional Geometry, collected from various examinations.

Question 1:

Show that the three points A (2, 3, 4), B (–1, 2, – 3) and C (– 4, 1, – 10) are collinear and find the ratio in which C divides AB.

Solution:
Given:
A(2,3,4), B(-1,2,-3) & C(-4,1,-10)
Now,
AB = $\sqrt{(2+1)^{2}+(3-2)^{2}+(4+3)^{2} }$
= $\sqrt{9+1+49 }$ = $\sqrt{59 }$
BC = $\sqrt{(-1+4)^{2}+(2-1)^{2}+(-3+10)^{2}}$
= $\sqrt{9+1+49 }$ = $\sqrt{59 }$
AC = $\sqrt{(2+4)^{2}+(3-1)^{2}+(4+10)^{2} }$
= $\sqrt{36+4+196 }$ = $2\sqrt{59}$
Now, AB + BC = $\sqrt{59}+\sqrt{59}$
= $2\sqrt{59}$
= AC
Thus, A, B & C are collinear.AC:BC = $2\sqrt{59}:\sqrt{59}$ = 2:1
Thus, C divides AB externally in the ratio 2:1.

Question 2:

What is the length of the foot of the perpendicular drawn from the point P (3, 4, 5) on the y-axis
A. $\sqrt{41}$
B. $\sqrt{34}$
C. 5
D. None of these

Solution:

The answer is the option (b)$\sqrt{ 34}$
On y-axis, x = z = 0
Thus, A = (0,4,0)
Thus, PA
= $\sqrt{ (0-3)^{2}+(4-4)^{2}+(0-5)^{2} }$
= $\sqrt{ 9+0+25 }$
= $\sqrt{ 34 }$

Hence, the correct answer is option B.

Question 3:

The distance of the point (3, 4, 5) from the origin (0, 0, 0) is
A. $\sqrt{50}$
B. 3
C. 4
D. 5

Solution:
The answer is the option (a) $\sqrt{50}$
Given: P(3,4,5) & O(0,0,0)
Thus, OP
= $\sqrt{(0-3)^{2}+(0-4)^2+(0-5)^{2} }$
= $\sqrt{9+16+25}$
= $\sqrt{50}$

Hence, the correct answer is option A.

Importance of NCERT Class 11 Maths Chapter 11 Notes

NCERT Class 11 Maths Chapter 11 Notes play a vital role in helping students grasp the core concepts of the chapter easily and effectively, so that they can remember these concepts for a long time. Some important points of these notes are:

• Effective Revision: These notes provide a detailed overview of all the important theorems and formulas, so that students can revise the chapter quickly and effectively.
• Clear Concepts: With these well-prepared notes, students can understand the basic concepts effectively. Also, these notes will help the students remember the key concepts by breaking down complex topics into simpler and easier-to-understand points.
• Time Saving: Students can look to save time by going through these notes instead of reading the whole lengthy chapter.
• Exam Ready Preparation: These notes also highlight the relevant content for various exams, so that students can get the last-minute guidance for exams.

NCERT Class 11 Maths Notes – Chapter-Wise Links

We at Careers360 compiled all the NCERT class 11 Maths notes in one place for easy student reference. The following links will allow you to access them.

Subject-Wise NCERT Notes

Given below are some subject-wise links for the NCERT Notes for class 11.

• NCERT Notes Class 11 Physics
• NCERT Notes Class 11 Chemistry
• NCERT Notes Class 11 Biology

Subject-Wise NCERT Exemplar Solutions

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better understanding of the concepts.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

Students can also check these well-structured, subject-wise solutions.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and NCERT Syllabus

Students should always analyse the latest syllabus before making a study routine. The following links will help them check the syllabus and access some reference books.

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11