Relations And Functions Class 11th Notes - Free NCERT Class 11 Maths Chapter 2 notes - Download PDF

In every school, each student has a unique ID number, and in the school’s database, that ID number represents the relation to that specific student. Similarly, in Mathematics, the Relations and Functions chapter discusses the connection between elements of two sets and their mapping. Also, this chapter includes the domain, co-domain, range, and graphing of a function. Relations and Functions Class 11 Notes are useful for calculus chapters (Differentiation and Integration) as well as algebra and coordinate geometry. The main purpose of these NCERT Notes of the Relations and Functions class 11 PDF is to provide students with an efficient study material from which they can revise the entire chapter.

After going through the textbook exercises and solutions, students need a type of study material from which they can recall concepts in a shorter time. Relations and Functions Class 11 Notes are very useful in this regard. In this article about NCERT Class 11 Maths Notes, everything from definitions and properties to detailed notes, formulas, diagrams, and solved examples is fully covered by our subject matter experts at Careers360 to help the students understand the important concepts and feel confident about their studies. These NCERT Class 11 Maths Chapter 2 Notes are made in accordance with the latest CBSE syllabus while keeping it simple, well-structured and understandable. For the syllabus, solutions, and chapter-wise PDFs, head over to this link: NCERT.

Relations and Functions Class 11 Notes: Free PDF Download

Use the link below to download the Relations and Functions Class 11 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 11 Maths Chapter 2 Notes: Relations and Functions

Understanding how elements connect and interact with each other is at the heart of mathematics, and NCERT Class 11 Maths Chapter 2: Relations and Functions lays the foundation for just that.

Ordered Pair: Two elements form an ordered pair.

Representation: (a,b)

NOTE: 2 ordered pairs (a, b) and (c, d) are said to be equal if (a=c) and (b=d)

Cartesian Product

If sets A and B have an ordered pair of (a,b) where aA and bB are called the Cartesian product.

Denoted by: A x B

Set builder form: A x B ={(a,b) : a ∈A and b∈ B}

NOTE:

1. If A=∅ , B= ∅, then the cartesian product A x B=∅.

2. It doesn’t satisfy the commutative law: (A, B)≠(B, A)

3. If either of the two sets is an infinite set, then the whole product becomes infinite.

A = infinite, B = finite, then A x B and B x A are also infinite.

4. If n(A) = m (m = number of elements in A), n(B) = n, then the number of elements in the Cartesian product is mn.

Eg: n(A) = 3 and n(B) = 2 then n(A x B) = 6.

Relations

A group of ordered pairs containing one element from each set is called a relation between two sets. Suppose A, and B are both non-empty sets, then the relation is a subset of the Cartesian product of (A x B).

A subset is a relation between the first and second elements of ordered pairs in A x B.

The set of first elements in relations is called the domain, and the next element is called the image or range of R.

Set builder form: R={(a,b): (a,b)∈R}

Representation Of Relation

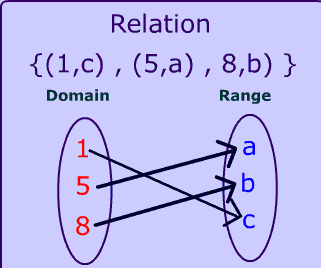
Note:

• The range can be represented in sand et-builder, roaster form, and also using arrow marks, with brackets.
• If n(A) = m (m = number of elthe ements in A), n(B) = n, and cartesian product=mn then a number of relations caound by using $2^{mn}$

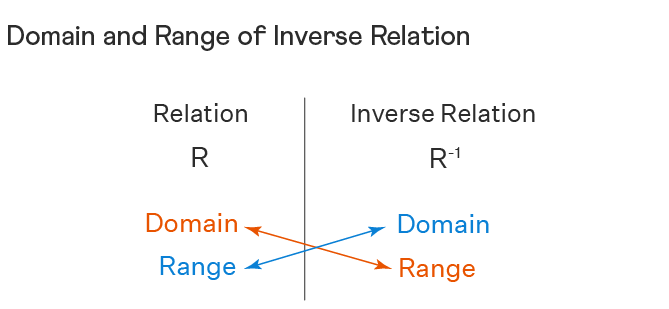
Inverse Relation

Sets A and B are both non-empty sets with $R$ being the relation, and the inverse of the relation is called the inverse relation $R^{-1}$ from B to A.

Set builder form : $R^{-1}=\{(b,a):(a,b)\in R\}$

The domain of the relation R will be the range of the inverse relation $R^{-1}$. The range of the relation R will be the domain of the inverse relation $R^{-1}$

Function

A relation F from A to B is called a function if every element in set A of a function has only one image in set B of a function.

A relation $f$ from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.

In other words, a function $f$ is a relation such that no two pairs in the relation have the same first element.

The notation $f:\mathrm{X}\to \mathrm{Y}$ means that $f$ is a function from X to $\mathrm{Y}.\mathrm{X}$ is called the domain of $f$ and Y is called the co-domain of $f$. Given an element $x\in \mathrm{X}$, there is a unique element $y$ in Y that is related to $x$. The unique element $y$ to which $f$ relates $x$ is denoted by $f(x)$ and is called $f$ of $x$, or the value of $\mathit{f}$ at $\mathit{x}$, or the image of $x$ under $f$.

The set of all values of $f(x)$ taken together is called the range of $f$ or image of X under $f$. Symbolically.

range of $f=\{y\in \mathrm{Y}\mid y=f(x)$, for some $x$ in X$\}$

Real-Valued Functions

Function denoted as f: A→B is said to be a real-valued function if B is a subset of R . If A, and B are subsets of R, in such conditions, we can call f a real function.

Type Of Functions:

Identity function:

A function is said to be an identity function if a function f: R→R when f(x)=x for each x belonging to R satisfies.

Consider the graph of an identity function f(x)=x:

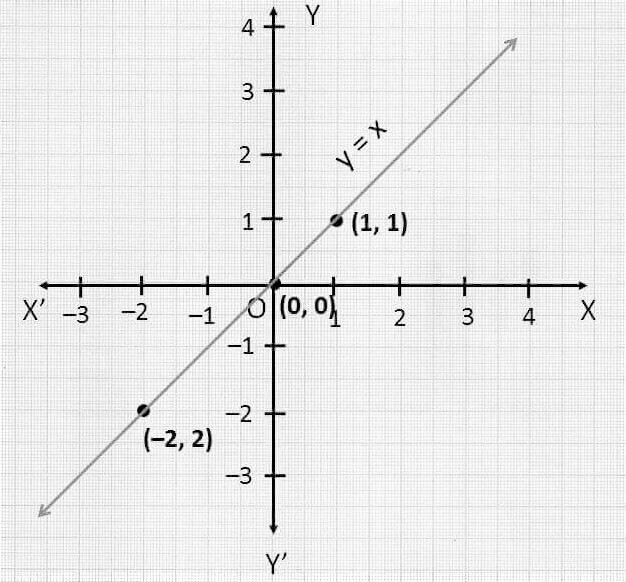
Domain= R

Range = C

Constant Function:

A function is said to be a constant function if a function f: R R when f(x)=C for each C belonging to R.

Consider the graph of a constant function:

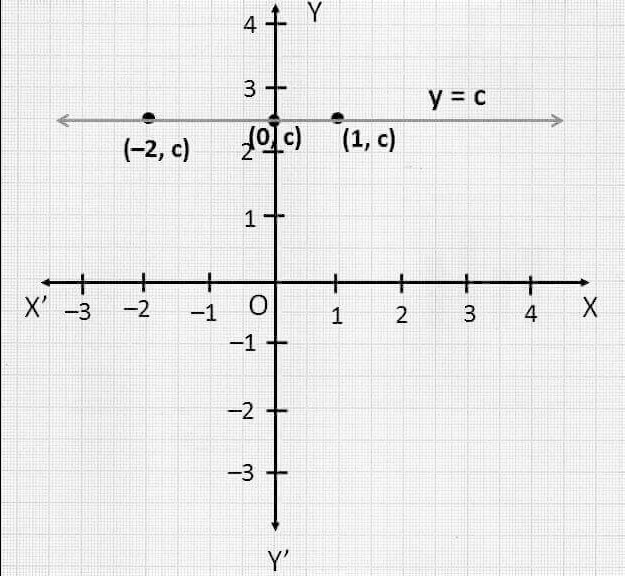
Domain= R

Range = C

Polynomial Function:

A function is said to be a Polynomial function if a function f: RR when each x belonging to R satisfies.

Rational Functions:

The functions that belong to Real functions, and are represented as f(x)/g(x) where f(x) and g(x) ≠ 0, are polynomial functions that are represented using x, and they belong to R.

Modulus Function:

Real function f: R → R is said to be a modulus function if

$f(x)=|x|$ for all x belongs to R
Domain: $R$
Range : $R^{+}\cup 0$ in the interval $[0,\mathrm{\infty })$

$f(x)=\left\{\begin{array}{cc}-x& \text{ if }x<0\\ x& \text{ if }x\ge 0\end{array}\right\}$

Signum Function:

Real function f: R → R is said to be a Signum function if f(x) = lxl / x where x≠0 and when x = 0 we get

$f(x)=\{\begin{array}{cc}1,& \text{ if }x>0\\ 0,& \text{ if }x=0\\ -1,& \text{ if }x<0\end{array}$

Domain= R

Range={-1,0,1}

Greatest Integer Function:

Real function f: R → R is said to be the greatest integer function if f(x)=[x] where x belongs to R and values of x are the greatest integer or less than or equal to x.

Fractional Function:

Real function f: R → R is said to be a rational function if f(x)={x} where x belongs to R.

f(x) = {x} = x – [x]

Domain: R

Range : [0,1)

Algebra of Real Functions

Addition Of Two Algebraic Functions:

If f: X → R and g: X →R are real functions, then we represent: (f + g): X → R as (f + g) (x) = f (x) + g(x) where x belongs to X.

Subtraction Of Real Functions:

If f: X → R and g: X → R are real functions, then we represent : (f – g): → R as (f – g) (x) = f (x) – g(x) where x belongs to X.

Multiplication Of Scalar:

If f: X → R is a real function, K is any scalar

The product of Kf is defined by : (Kf)(x) = Kf(x)

Multiplication Of Two Real Functions:

If f: → R and g: X→ R are real functions,

The product of the two functions is defined by: (fg) x = f(x). gx)

The Quotient Of Two Real Functions:

If f and g are two real functions, then the

The quotient of f by g is given by fg from XR.

(f/g)(x) = f(x)/g(x) where g(x)≠0

With this topic, we conclude the NCERT Class 11 Maths Chapter 2 Notes.

Relations and Functions: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 11 chapter 2, Relations and Functions:

NCERT Class 11 Notes Chapter Wise

All the links of chapter-wise notes for NCERT class 11 maths are given below:

Subject-Wise NCERT Exemplar Solutions

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better understanding of the concepts.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11x Biology

Subject-Wise NCERT Solutions

Students can also check these well-structured, subject-wise solutions.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus

Students should always analyse the latest CBSE syllabus before making a study routine. The following links will help them check the syllabus. Also, here is access to more reference books.

• NCERT Book for Class 12
• NCERT Syllabus for Class 12