Binomial Theorem Class 11th Notes - Free NCERT Class 11 Maths Chapter 8 notes - Download PDF

Class 11 Binomial Theorem Notes PDF – Download Free Study Material

Students who wish to access the Binomial Theorem Class 11 Maths notes can click on the link below to download the entire notes in PDF.

Download PDF

Binomial Theorem Class 11 Notes

Careers360 has prepared these Class 11 Binomial Theorem Notes to make your revision smoother and faster.

We know,
$
\begin{aligned}
& (a+b)^0=1 \\
& (a+b)^1=a+b \\
& (a+b)^2=a^2+2 a b+b^2 \\
& (a+b)^3=a^3+3 a^2 b+3 a b^2+b^3
\end{aligned}
$

If we observe each expansion,

• The total number of terms of each expansion is 1 more than the index of $(a+b)$.

• In the expansion, the power of the first quantity is gradually decreasing by 1, and the power of the second quantity is gradually increasing by 1.

• Suppose n is the index of $(a+b)$; then the sum of the indices of a and b of each term of the expansion is n.

Now, we arrange the coefficients of expansion with respect to their index.

If we observe the pattern, we can get the coefficient of the next index.

The pattern is given below.

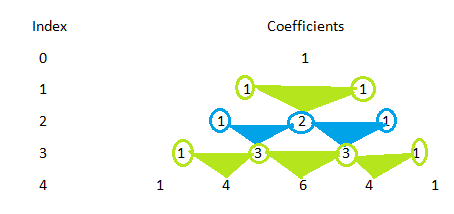
Figure: 1

This diagram is known as Pascal's triangle.

If we apply Pascal's triangle rule, then the coefficients of $(a+b)^5$ will be 1 5 10 10 5 1.

Similarly, the coefficient of $(a+b)^6$ will be 1 6 15 20 15 6 1.

Now, we can apply the combination formula to find the coefficients.

Binomial coefficient (for a Positive integral index n) ${ }^n C_r=\frac{n!}{(n-r)!r!}$,
where n and r are positive integers and $0 \leq r<n$.

Figure 2 can be rewritten as:

Index Coefficients

$
\begin{aligned}
& 0 \quad{ }^0 C_0(=1) \\
& 1 \quad{ }^1 C_0(=1) \quad{ }^1 C_1(=1) \\
& 2 \quad{ }^2 C_0(=1) \quad{ }^2 C_1(=2) \quad{ }^2 C_2(=1) \\
& 3 \quad{ }^3 C_0(=1) \quad{ }^3 C_1(=3) \quad{ }^3 C_3(=3) \quad{ }^3 C_3(=1) \\
& 4 \quad{ }^4 C_0(=1) \quad{ }^4 C_1(=4) \quad{ }^4 C_2(=6) \quad{ }^4 C_3(=4) \quad{ }^4 C_4(=1)
\end{aligned}
$

Binomial Theorem

Binomial theorem for any positive integer $n$,
$
(a+b)^n={ }^n \mathrm{C}_0 a^n+{ }^n \mathrm{C}_1 a^{n-1} b+{ }^n \mathrm{C}_2 a^{n-2} b^2+\ldots+{ }^n \mathrm{C}_{n-1} a \cdot b^{n-1}+{ }^n \mathrm{C}_n b^n
$

Proof:
The proof is obtained by applying the principle of mathematical induction.
Let the given statement be

$
\mathrm{P}(n):(a+b)^n={ }^n \mathrm{C}_0 a^n+{ }^n \mathrm{C}_1 a^{n-1} b+{ }^n \mathrm{C}_2 a^{n-2} b^2+\ldots+{ }^n \mathrm{C}_{n-1} a \cdot b^{n-1}+{ }^n \mathrm{C}_n b^n
$
For $n=1$, we have

$
\mathrm{P}(1):(a+b)^1={ }^1 \mathrm{C}_0 a^1+{ }^1 \mathrm{C}_1 b^1=a+b
$
Thus, $\mathrm{P}(1)$ is true.
Suppose $\mathrm{P}(k)$ is true for some positive integer $k$, i.e.

$
(a+b)^k={ }^k \mathrm{C}_0 a^k+{ }^k \mathrm{C}_1 a^{k-1} b+{ }^k \mathrm{C}_2 a^{k-2} b^2+\ldots+{ }^k \mathrm{C}_k b^k
---(1)$

We shall prove that $\mathrm{P}(k+1)$ is also true, i.e.,

$
(a+b)^{k+1}={ }^{k+1} \mathrm{C}_0 a^{k+1}+{ }^{k+1} \mathrm{C}_1 a^k b+{ }^{k+1} \mathrm{C}_2 a^{k-1} b^2+\ldots+{ }^{k+1} \mathrm{C}_{k+1} b^{k+1}
$

Now, $(a+b)^{k+1}=(a+b)(a+b)^k$

$
\begin{aligned}
= & (a+b)\left({ }^k \mathrm{C}_0 a^k+{ }^k \mathrm{C}_1 a^{k-1} b+{ }^k \mathrm{C}_2 a^{k-2} b^2+\ldots+{ }^k \mathrm{C}_{k-1} a b^{k-1}+{ }^k \mathrm{C}_k b^k\right) \\
\quad & \quad \text { from (1)] } \\
= & { }^k \mathrm{C}_0 a^{k+1}+{ }^k \mathrm{C}_1 a^k b+{ }^k \mathrm{C}_2 a^{k-1} b^2+\ldots+{ }^k \mathrm{C}_{k-1} a^2 b^{k-1}+{ }^k \mathrm{C}_k a b^k+{ }^k \mathrm{C}_0 a^k b \\
& +{ }^k \mathrm{C}_1 a^{k-1} b^2+{ }^k \mathrm{C}_2 a^{k-2} b^3+\ldots+{ }^k \mathrm{C}_{k-1} a b^k+{ }^k \mathrm{C}_k b^{k+1}
\end{aligned}
$
[by actual multiplication]

$
\begin{aligned}
&={ }^k \mathrm{C}_0 a^{k+1}+\left({ }^k \mathrm{C}_1+{ }^k \mathrm{C}_0\right) a^k b+\left({ }^k \mathrm{C}_2+{ }^k \mathrm{C}_1\right) a^{k-1} b^2+\ldots \\
&+\left({ }^k \mathrm{C}_k+{ }^k \mathrm{C}_{k-1}\right) a b^k+{ }^k \mathrm{C}_k b^{k+1} [\text{By grouping like terms}]\\
&={ }^{k+1} \mathrm{C}_0 a a^{k+1}+{ }^{k+1} \mathrm{C}_1 a^k b+{ }^{k+1} \mathrm{C}_2 a^{k-1} \mathrm{~b}^2+\ldots+{ }^{k+1} \mathrm{C}_k a b^k+{ }^{k+1} \mathrm{C}_{k+1} b^{k+1}
\end{aligned}
$

(by using ${ }^{k+1} \mathrm{C}_0=1,{ }^k \mathrm{C}_r+{ }^k \mathrm{C}_{r-1}={ }^{k+1} \mathrm{C}_r \quad$ and ${ }^k \mathrm{C}_k=1={ }^{k+1} \mathrm{C}_{k+1}$ )
Thus, it has been proved that $\mathrm{P}(k+1)$ is true whenever $\mathrm{P}(k)$ is true. Therefore, by the principle of mathematical induction, $\mathrm{P}(n)$ is true for every positive integer $n$.

Properties of the Binomial Coefficient

1. $n!=n(n-1)(n-2)(n-3) \ldots \ldots \ldots .4 \times 3 \times 2 \times 1$
2. ${ }^n C_r={ }^n C_{n-r}$
$⇒{ }^n C_r=\frac{n!}{(n-r)!r!}$
and
${ }^n C_{n-r}=\frac{n!}{(n-r)!(n-n+r)!}$
$⇒{ }^n C_{n-r}=\frac{n!}{(n-r)!(r)!}$
Hence, it is proven that both are equal.
3. If ${ }^n C_x={ }^n C_y$ only if $x=y$ and $x+y=n$
4. ${ }^n C_r+{ }^n C_{r-1}={ }^{n+1} C_r$
5. If n is a positive integer and $\mathrm{x}, \mathrm{y}$ are two complex numbers, then $(x+y)^n={ }^n C_0 x^n+{ }^n C_1 x^{n-1} y \ldots \ldots \ldots \ldots \ldots .{ }^n C_{n-1} x y^{n-1}+{ }^n C_n y^n$

Here binomial coefficients are: ${ }^n C_0,{ }^n C_1, \ldots \ldots \ldots \ldots \ldots . .{ }^n C_{n-1},{ }^n C_n$

6. Total no. of terms of the given as $(n+1)$ in the expansion
$(x+y)^n={ }^n C_0 x^n+{ }^n C_1 x^{n-1} y \ldots \ldots \ldots \ldots \ldots .{ }^n C_{n-1} x y^{n-1}+{ }^n C_n y^n$

To find the middle terms of using the Binomial theorem

The general equation of the binomial is given as:

$
\begin{aligned}
& (x+y)^n={ }^n C_0 x^n+{ }^n C_1 x^{n-1} y \ldots \ldots \ldots \ldots \ldots .{ }^n C_{n-1} x y^{n-1}+{ }^n C_n y^n \\
& (x+y)^n=T_1+T_2+T_3 \ldots \ldots \ldots \ldots \ldots . T_n+T_{n+1}
\end{aligned}
$

There are two cases.
1. If n is odd.

The number of terms of $(a+b)^n$ when $n$ is an odd number is $n+1$.
Here, $n+1$ is an even number.
So there will be two middle terms.
That are $\left(\frac{n+1}{2}\right)^{\text {th }}$ and $\left(\frac{n+1}{2}+1\right)^{t h}$ terms of the expansion.

2. If n is even

The number of terms of $(a+b)^n$ when $n$ is an even number is $n+1$.
Here, $n+1$ is an odd number.
So there will be one middle term.
That is $\left(\frac{n+1+1}{2}\right)^{t h}=\left(\frac{n}{2}+1\right)^{t h}$ term of the expansion.

To find the sum of the coefficients of the binomial terms, we have to put the value of $x$ numerically as one.

For example
Q. If the binomial expression is $(x-y+1)^4$, then find the sum of the binomial coefficients is?

Solution: We have to put the value of $x=y=1$ and get the coefficient sum.
$(x-y+1)^4$
$
\begin{aligned}
& =(1-1+1)^4 \\
& =1
\end{aligned}
$
So the Sum of the binomial coefficients is 1.

Some Properties of the Binomial Coefficients

$
(x+y)^n={ }^n C_0 x^n+{ }^n C_1 x^{n-1} y \ldots \ldots \ldots \ldots \ldots . .{ }^n C_{n-1} x y^{n-1}+{ }^n C_n y^n
$
Put $x=y=1$
$
\begin{aligned}
&⇒ (1+1)^n={ }^n C_0 11^n+{ }^n C_1 1{ }^{n-1} 1 \ldots \ldots \ldots \ldots \ldots .{ }^n C_{n-1} 1.1^{n-1}+{ }^n C_n 1^n \\
&⇒ (2)^n={ }^n C_0+{ }^n C_1 \ldots \ldots \ldots \ldots \ldots .{ }^n C_{n-1}+{ }^n C_n
\end{aligned}
$

$ (x+y)^n={ }^n C_0 x x^n+{ }^n C_1 x x^{n-1} y \ldots \ldots \ldots \ldots \ldots .{ }^n C_{n-1} x y^{n-1}+{ }^n C_n y^n$
Put $x=-y=1$
$
\begin{aligned}
&⇒ (1-1)^n={ }^n C_0 1^n+{ }^n C_1 1{ }^{n-1}(-1) \ldots \ldots \ldots \ldots . . \ldots{ }^n C_{n-1} 1 .(-1)^{n-1}+{ }^n C_n(-1)^n \\
&⇒ 0={ }^n C_0-{ }^n C_1 \ldots \ldots \ldots \ldots \ldots . .{ }^n C_{n-1}(-1)^n+{ }^n C_n(-1)^n
\end{aligned}
$

Some Particular expansions

$
\begin{aligned}
& (1+x)^{-1}=1-x+x^2-x^3 \ldots \ldots . . \\
& (1-x)^{-1}=1+x+x^2+x^3 \ldots \ldots ... \\
& (1+x)^{-2}=1-2 x+3 x^2-4 x^3 . .... \\
& (1-x)^{-2}=1+2 x+3 x^2+4 x^3 . ....
\end{aligned}
$

Binomial Theorem: Previous Year Question and Answer

Given below are selected previous year question answers for NCERT Class 11 Maths Chapter 7 Binomial Theorem, collected from various examinations.

Question 1:

Find the term independent of x, where x≠0, in the expansion of $\left ( \frac{3x^{2}}{2} - \frac{1}{3x} \right )^{15}$

Solution:
$\left ( \frac{3x^{2}}{2} - \frac{1}{3x} \right )^{15}$............... (Given)
$T_{r+1}=^{15}\textrm{C}_{r}\left ( \frac{3x^{2}}{2} \right )^{15-r}\left ( -\frac{1}{3x} \right )^{r}$ ……. (from standard formula of Tr+1)
$\Rightarrow T_{r+1}=^{15}\textrm{C}_{r}\left ( -1 \right )^{r}3^{15-2r}2^{r-15}X^{30-3r}$ …… (i)
Now, for x,
30 – 3r = 0
$\Rightarrow$r = 10
Substituting the value of r in eq (i),

$T_{r+1}=^{15}\textrm{C}_{10}3^{-5}2^{-5}$
$=\ ^{15}\textrm{C}_{10}\left ( \frac{1}{6} \right )^{5}$

Question 2:

Find the value of r, if the coefficients of (2r + 4)^th and (r – 2)^th terms in the expansion of (1 + x)¹⁸ are equal.

Solution:
Given: (1+x)¹⁸
Now, T_(2r+3)+1is the (2r + 4)^th term
Thus, T_(2r+3)+1 = ¹⁸C_2r+3 (x)^2r+3
Now, T_(r-3)+1 is the (r-2)^th term
Thus, T_(r-3)+1 = ¹⁸C_r-3 x^r-3
Now, it is given that the terms are equal in expansion.
Thus,
¹⁸C_2r+3= ¹⁸C_r-3
i.e., 2r + 3 + r – 3 = 18 …… (ⁿC_x = ⁿC_y gives x + y = n)
Thus, 3r = 18
Therefore, r = 6

Question 3:

Find n in the binomial $\left (\sqrt[3]{2} +\frac{1}{\sqrt[3]{3}} \right )^{n}$ if the ratio of 7th term from the beginning to the 7th term from the end is $\frac{1}{6}$

Solution:
Given $\left ( \sqrt[3]{2}+\frac{1}{\sqrt[3]{3}} \right )^{n}$
Now, from the beginning,
Seventh term is $T_{7}=T_{6+1}$
$=^{n}C_{6} \left (\sqrt[3]{2} \right )^{n-6}\left ( \frac{1}{\sqrt[3]{3}} \right )^{6}$...................(i)
& from the end,
The seventh term is the same ,i.e., $\left (\frac{1}{\sqrt[3]{3}}+\sqrt[2]{3} \right )^{n}$
$T_{7}=^{n}C_{6}\left ( \frac{1}{\sqrt[3]{3}} \right )^{n-6}\left ( \sqrt[3]{2} \right )^{6}$.............(ii)
Now, it is given that
$\frac{^{n}C_{6}\left (\sqrt[3]{2} \right )^{n-6}\left ( \frac{1}{\sqrt[3]{3}} \right )^{6}}{^{n}C_{6}\left ( \frac{1}{\sqrt[3]{3}} \right )^{n-6}\left ( \sqrt[3]{2} \right )^{6}} = \frac{1}{6}$
Thus
$\frac{\left ( \sqrt[3]{2} \right )^{n-12}}{\left (\frac{1}{\sqrt[3]{3}} \right )^{n-12} }=\frac{1}{6}$
Thus $(\sqrt[3]{2} \sqrt[3]{3})^{n-12}=6^{-1}$

Thus $6^\frac{n-12}{3}=6^{-1}$
$\frac{n-12}{3}=-1$
Thus $n=9$

Importance of NCERT Class 11 Math Chapter 7 Notes

NCERT Class 11 Maths chapter 7 notes are useful in many ways.

• These notes will give conceptual clarity about the Binomial theorem and build a strong base for the Algebra, Calculus, and Probability chapter, which is not only important for board exams in 11 and 12 but also for other competitive exams like JEE Main, NDA, CUET, etc.
• These notes will teach how to use the Binomial theorem efficiently to save time by not doing repeated multiplication.
• Students can use these notes for a quick revision whenever they need.
• These notes contain PDF links to other subjects' solutions.
• The latest CBSE Class 11 Maths syllabus guidelines have been followed in these notes.
• Experts who have multiple years of experience in these topics have created these notes so that students can learn these concepts easily.

NCERT Class 11 Maths Notes – Chapter-Wise Links

Access all NCERT Class 11 Maths notes from one place using the links below.

Subject-Wise NCERT Exemplar Solutions

NCERT exemplar is one of the best study materials for revision and practice purposes. After completing the exercises, they can compare their solutions with the solved ones.

• NCERT Exemplar Class 11 Solutions

• NCERT Exemplar Class 11 Maths

• NCERT Exemplar Class 11 Physics

• NCERT Exemplar Class 11 Chemistry

• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

Students can use the following links to analyse the NCERT textbook solutions for other subjects.

• NCERT Solutions for Class 11 Mathematics

• NCERT Solutions for Class 11 Chemistry

• NCERT Solutions for Class 11 Physics

• NCERT Solutions for Class 11 Biology

NCERT Books and NCERT Syllabus

Students should always have access to the latest NCERT syllabus, and the following link will give them that privilege. Also, they can access some reference books using the links below.

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11