Trigonometric Functions Class 11th Notes - Free NCERT Class 11 Maths Chapter 3 notes - Download PDF

NCERT Notes for Class 11 Chapter 3 Trigonometric Functions: Free PDF Download

Students who wish to access these NCERT Class 11 Maths Chapter 3 Notes can click on the link below to download the entire notes in PDF format.

Download PDF

Trigonometric Functions Class 11 Notes

These Trigonometric Functions Class 11th Notes, prepared by Careers360 experts, are designed to make your revision easy and efficient.

Trigonometry: Trigon means three sides, and it is a triangle.
And Metry means measurement.

Angle

Angle is the measure of rotation of a ray from its initial point, which is generally denoted by θ.

We have both positive and negative angles. They are represented as follows:

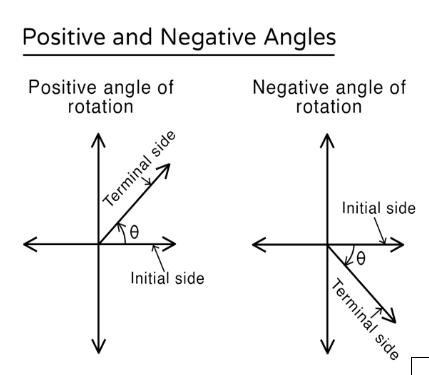
Degree

One degree has 60 minutes, and one minute is further divided into 60 seconds. If a ray rotates from one initial point to another end or terminal point, then it is said to cover $\frac1{360}^{\text{th}}$, then it is said to be 1° (one degree)

Radian

It is another unit to measure angles. The angle measured at the centre forming an arc of 1 unit length in a unit circle with a radius being 1 is called a measure of 1 radian.

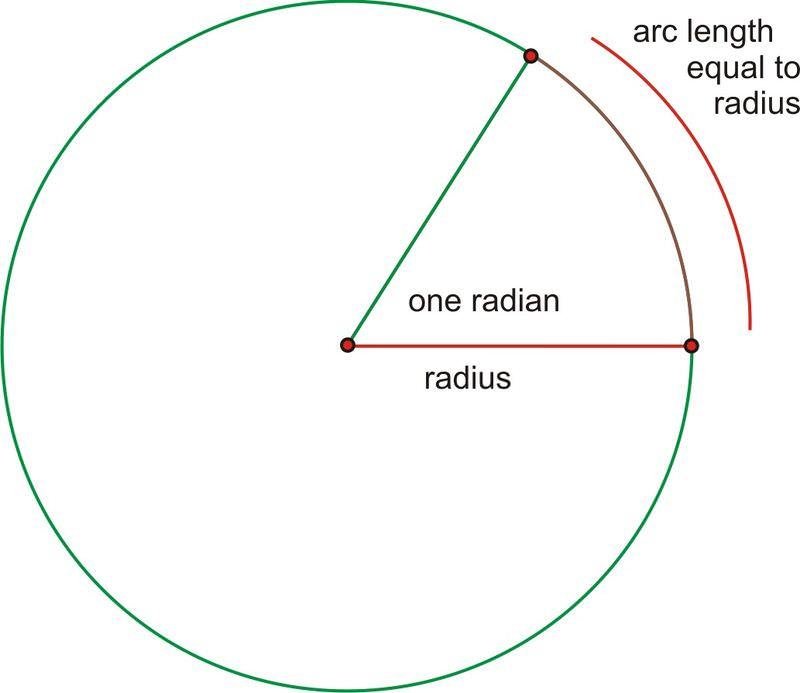
Formula:
$\theta=\frac{\text { arc length }}{\text { radius }}=\frac lr$
$⇒ l= rθ$

$l =$ length made by the arc

$r =$ radius of the circle

$θ =$ angle measure.

Relation Between Degree And Radian

To find the radian measure when the degree is given and vice versa.

1 radian = $\frac{180°}{π}$

\[
\begin{array}{|c|c|c|}
\hline
\textbf{Degrees} & \textbf{Radians} & \textbf{Revolutions} \\ \hline
0 & 0 &0 \\ \hline
30 & \frac{\pi}{6} & \frac{1}{12} \\ \hline
45 & \frac{\pi}{4} & \frac{1}{8} \\ \hline
60 & \frac{\pi}{3} & \frac{1}{6} \\ \hline
90 & \frac{\pi}{2} & \frac{1}{4} \\ \hline
120 & \frac{2\pi}{3} & \frac{1}{3} \\ \hline
135 & \frac{3\pi}{4} & \frac{3}{8} \\ \hline
180 & \frac{\pi}{1} & \frac{1}{2} \\ \hline
225 & \frac{5\pi}{4} & \frac{5}{8} \\ \hline
270 & \frac{3\pi}{2} & \frac{3}{4} \\ \hline
315 & \frac{7\pi}{4} & \frac{7}{8} \\ \hline
360 & \frac{2\pi}{1} & \frac{1}{1} \\ \hline
\end{array}
\]

Conventional Measure

$
\text { Radian measure }=\left(\frac{\pi}{180^{\circ}}\right) \times \text { degree value }
$
$
\text { Degree measure }=\left(\frac{180^{\circ}}{\pi}\right) \times \text { radian value }
$

Trigonometric Functions

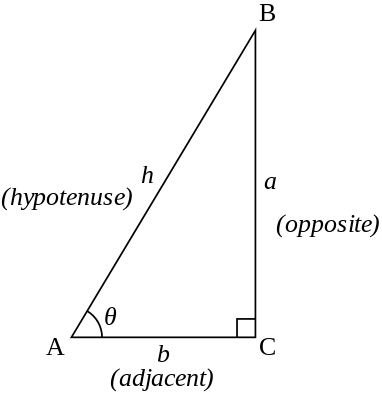
$\begin{aligned}
& \sin \theta=\frac{\text { opposite side }}{\text { hypotenuse }} \\
& \operatorname{cosec} \theta=\frac{\text { hypotenuse }}{\text { opposite } \operatorname{side}}=\frac{1}{\sin \theta} \\
& \cos \theta=\frac{\text { adjacent side }}{\text { hypotenuse }} \\
& \sec \theta=\frac{\text { hypotenuse }}{\text { adjacent } \operatorname{side}}=\frac{1}{\cos \theta} \\
& \tan \theta=\frac{\text { opposite side }}{\text { adjacent } \operatorname{side}}=\frac{\sin \theta}{\cos \theta} \\
& \cot \theta=\frac{\text { adjacent side }}{\text { opposite } \operatorname{side}}=\frac{\cos \theta}{\sin \theta}=\frac{1}{\tan \theta}
\end{aligned}$

By the hypotenuse theorem:
$(\text { opposite side })^2+(\text { adjacent side })^2=(\text { hypotenuse })^2$
From the above right-angle theorem:

$(a)^2+(b)^2=(h)^2$

We have a few identities:

$\begin{aligned} & \sin ^2 \theta+\cos ^2 \theta=1 \\ & 1+\tan ^2 \theta=\sec ^2 \theta \\ & 1+\cot ^2 \theta=\operatorname{cosec}^2 \theta\end{aligned}$

Table to be remembered

$\begin{array}{|c|c|c|c|c|c|c|}
\hline \hline \mathrm{A} & \sin \mathrm{~A} & \cos \mathrm{~A} & \tan \mathrm{~A} & \cot \mathrm{~A} & \sec \mathrm{~A} & \operatorname{cosec} \mathrm{~A} \\
\hline \hline 0^{\circ} & 0 & 1 & 0 & \infty & 1 & \infty \\
\hline 30^{\circ} & \frac12 & \frac{\sqrt{3}} 2 & \frac1 {\sqrt{3}} & \sqrt{3} & \frac2 {\sqrt{3}} & 2 \\
\hline 45^{\circ} & \frac{ \sqrt{2}} 2 & \frac{ \sqrt{2}} 2 & 1 & 1 & \sqrt{2} & \sqrt{2} \\
\hline 60^{\circ} & \frac{\sqrt{3}} 2 & \frac12 & \sqrt{3} & \frac1 {\sqrt{3}} & 2 & \frac2 {\sqrt{3}} \\
\hline 90^{\circ} & 1 & 0 & \infty & 0 & \infty & 1 \\
\hline \hline
\end{array}$

Sign of Trigonometric Functions

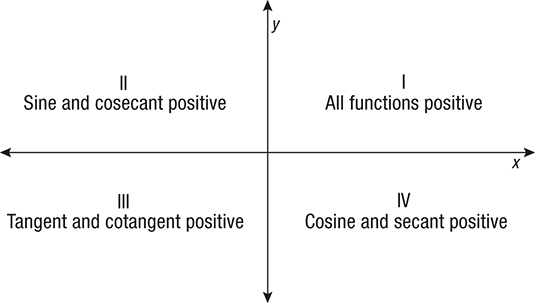
From the above diagram, we can find the sign of the trigonometric functions.

Some points to remember

$\begin{aligned} & \sin (-x)=-\sin (x) \\ & \cos (-x)=\cos (x) \\ & \tan (-x)=-\tan (x) \\ & \cot (-x)=-\cot (x) \\ & \sec (-x)=\sec (x) \\ & \operatorname{cosec}(-x)=-\operatorname{cosec}(x)\end{aligned}$

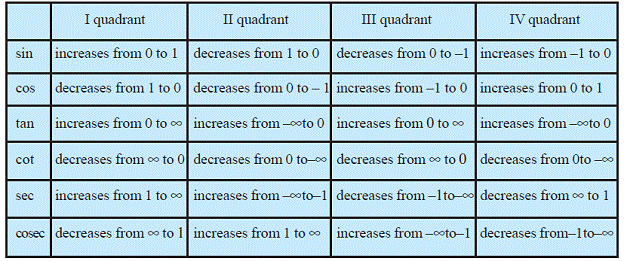
Domain and Range of Trigonometric Functions

Formula:

$\begin{aligned} & \sin (x+y)=\sin x \cdot \cos y+\cos x \cdot \sin y \\ & \sin (x-y)=\sin x \cdot \cos y-\cos x \cdot \sin y \\ & \cos (x+y)=\cos x \cdot \cos y-\sin x \cdot \sin y \\ & \cos (x-y)=\cos x \cdot \cos y+\sin x \cdot \sin y \\ & \tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \cdot \tan y} \\ & \tan (x-y)=\frac{\tan x-\tan y}{1+\tan x \cdot \tan y} \\ & \cot (x+y)=\frac{\cot x \cdot \cot y-1}{\cot x+\cot y} \\ & \cot (x-y)=\frac{\cot x \cdot \cot y+1}{\cot y-\cot x}\end{aligned}$

Graphs of Trigonometric Functions

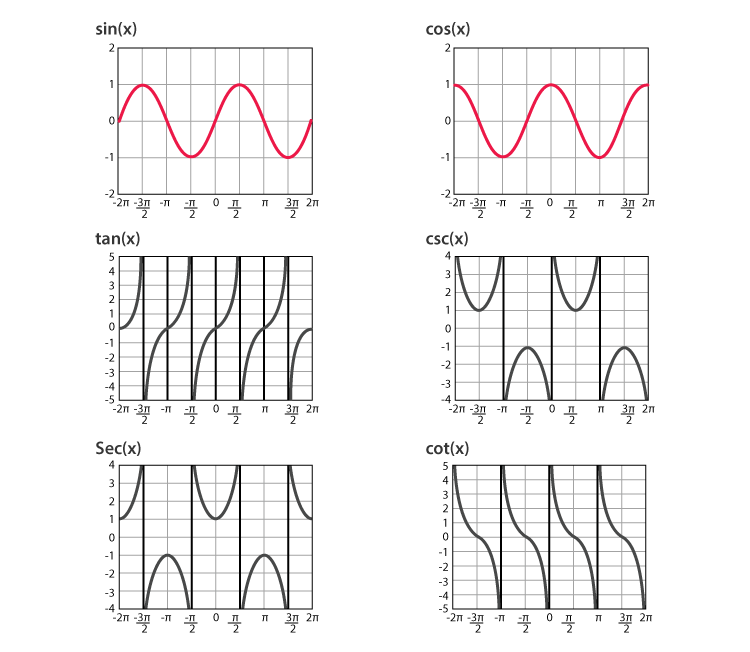
Transformation Formulas

$\begin{aligned} & \sin (x+y)+\sin (x-y)=2 \sin x \cdot \cos y \\ & \sin (x+y)-\sin (x-y)=2 \cos x \cdot \sin y \\ & \cos (x+y)+\cos (x-y)=2 \cos x \cdot \cos y \\ & \cos (x-y)-\cos (x+y)=2 \sin x \cdot \sin y \\ & \sin x+\sin y=2 \sin \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right) \\ & \sin x-\sin y=2 \cos \left(\frac{x+y}{2}\right) \sin \left(\frac{x-y}{2}\right) \\ & \cos x+\cos y=2 \cos \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right) \\ & \cos x-\cos y=-2 \sin \left(\frac{x+y}{2}\right) \sin \left(\frac{x-y}{2}\right) \\ & \sin 2 x=2 \sin x \cos x \\ & \cos 2 x=\cos ^2 x-\sin ^2 x=1-2 \sin ^2 x=2 \cos ^2 x-1 \\ & \sin 3 x=3 \sin x-4 \sin ^3 x \\ & \cos 3 x=4 \cos ^3 x-3 \cos ^2 x \\ & \tan 3 x=\frac{\left(3 \tan x-\tan ^3 x\right)}{1-3 \tan ^2 x} \\ & \cot 3 x=\frac{3 \cot x-\cot ^3 x}{1-3 \cot ^2 x}\end{aligned}$

How to Use the Trigonometric Functions Class 11 Notes Effectively?

Trigonometric Functions is one of the most important chapters in Class 11 because it helps us understand angles and their applications in real-life problems. This chapter becomes easier to understand when we learn it step by step with clear examples. Using these Class 11 Maths Chapter 3 notes correctly will make revision faster and more effective. Here are some more points on how these notes are important.

• Read the topics in order: Angles, Trigonometric Functions, and then Sum and Difference formulas, so the concepts build smoothly.
• Practice diagrams of small angles and make a table of basic trigonometric values while studying to remember them quickly.
• Link these concepts from your NCERT Class 11 Maths Chapter 3 notes to higher classes, because trigonometry is used in calculus, vectors, and even physics in Class 12.
• Go back to the NCERT Class 11 Maths Chapter 3 notes often and solve quick problems after each topic to check if you truly understand the formulas.

Trigonometric Functions Class 11 Notes: Previous Year Question and Answer

Given below are selected previous year question answers for NCERT Class 11 Maths Chapter 3 Trigonometric Functions, collected from various examinations.

Question 1: If $\operatorname{cosec} \theta+\cot \theta=\mathbf{s}$, then what is the value of $\cos \theta$?

Solution:

Given, $\operatorname{cosec} \theta+\cot \theta=\mathbf{s}$
We know, $\cot\theta = \frac{\cos\theta}{\sin\theta}$ and $\operatorname{cosec} \theta=\frac{1}{\sin\theta}$
⇒ $\frac{1}{\sin\theta}+\frac{\cos\theta}{\sin\theta}=s$
⇒ $\frac{1+\cos\theta}{\sin\theta}=s$
Squaring both sides, we get
⇒ $\frac{(1+\cos\theta)^2}{\sin^2\theta}=s^2$
We know, $\cos^2\theta+\sin^2\theta=1$
⇒ $\frac{1+\cos^2\theta+2\cos\theta}{1-\cos^2\theta}=s^2$
Applying componendo and dividendo,
⇒ $\frac{1+\cos^2\theta+2\cos\theta+1-\cos^2\theta}{1+\cos^2\theta+2\cos\theta-(1-\cos^2\theta)}=\frac{s^2+1}{s^2-1}$
⇒ $\frac{1+\cos^2\theta+2\cos\theta+1-\cos^2\theta}{1+\cos^2\theta+2\cos\theta-1+\cos^2\theta}=\frac{s^2+1}{s^2-1}$
⇒ $\frac{2+2\cos\theta}{2\cos^2\theta+2\cos\theta}=\frac{s^2+1}{s^2-1}$
⇒ $\frac{2(1+\cos\theta)}{2\cos\theta(\cos\theta+1)}=\frac{s^2+1}{s^2-1}$
⇒ $\frac{1}{\cos\theta}=\frac{s^2+1}{s^2-1}$
⇒ $\cos\theta=\frac{s^2-1}{s^2+1}$
Hence, the correct answer is $\frac{s^2-1}{s^2+1}$.

Question 2:
$\triangle $KLM is a right-angled triangle. $\angle$M = 90$^{\circ}$, KM = 12 cm and LM = 5 cm. What is the value of $\sec$ L?

Solution:
By Pythagoras' theorem,
KL² = KM² + ML²
⇒ KL = $\sqrt{12^2 + 5^2}$ = $\sqrt {144+69}$ = $\sqrt{169}$ = 13
$\therefore\sec$ L = $\frac{\text{KL}}{\text{ML}}$ = $\frac{13}{5}$
Hence, the correct answer is $\frac{13}{5}$.

Question 3:
If $\frac{\sin \theta}{\cot \theta+\operatorname{cosec} \theta}=1$, then what is the value of $\theta$?

Solution:
$\frac{\sin \theta}{\cot \theta+\operatorname{cosec} \theta}=1$
⇒ $\frac{\sin \theta}{\frac{\cos \theta}{\sin \theta} +\frac{1}{\sin \theta}}=1$
⇒ $\frac{\sin \theta}{\frac{1+\cos \theta}{\sin \theta}}=1$
⇒ $\frac{\sin^2 \theta}{1+\cos \theta}=1$
⇒ $\sin^2 \theta = 1+\cos \theta$
⇒ $1-\sin^2 \theta+\cos \theta = 0$
⇒ $\cos^2 \theta + \cos \theta = 0$ ($\because$ $ \sin^2 \theta+\cos^2 \theta =1$ )
⇒ $\cos \theta(1+ \cos \theta) = 0$
⇒ $\cos \theta= 0$ or $\cos \theta = –1$
⇒ $\theta = 90^{\circ}$ or $180^{\circ}$
Hence, the correct answer is $90^{\circ}$.

Importance of NCERT Class 11 Maths Chapter 3 Notes

NCERT Class 11 Maths Chapter 3 Notes play a vital role in helping students grasp the core concepts of the chapter easily and effectively, so that they can remember these concepts for a long time. Some important points of these notes are:

• Effective Revision: These notes provide a detailed overview of all the important theorems and formulas, so that students can revise the chapter quickly and effectively.
• Clear Concepts: With these well-prepared notes, students can understand the basic concepts effectively. Also, these notes will help the students remember the key concepts by breaking down complex topics into simpler and easier-to-understand points.
• Time Saving: Students can look to save time by going through these notes instead of reading the whole lengthy chapter.
• Exam Ready Preparation: These notes also highlight the relevant content for various exams, so that students can get the last-minute guidance for exams.

NCERT Class 11 Maths Notes Chapter-Wise Links

For students' preparation, Careers360 has gathered all Class 11 Maths NCERT Notes here for quick and convenient access.

NCERT Exemplar Solutions Subject-Wise

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better understanding of the concepts.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

Students can also check these well-structured, subject-wise solutions.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and NCERT Syllabus

Students should always analyse the latest syllabus before making a study routine. The following links will help them check the syllabus and some reference books.

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11