Complex Numbers And Quadratic Equations Class 11th Notes - Free NCERT Class 11 Maths Chapter 5 notes - Download PDF

Complex Numbers and Quadratic Equations Class 11 Notes: Free PDF Download

Use the link below to download the Complex Numbers and Quadratic Equations Class 11 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 11 Maths Chapter 4 Notes Complex Numbers and Quadratic Equations

Complex Numbers and Quadratic Equations help us solve equations that have no real solutions by introducing the imaginary number $i$. This chapter explores how complex numbers work and how they are used to find the roots of quadratic equations.

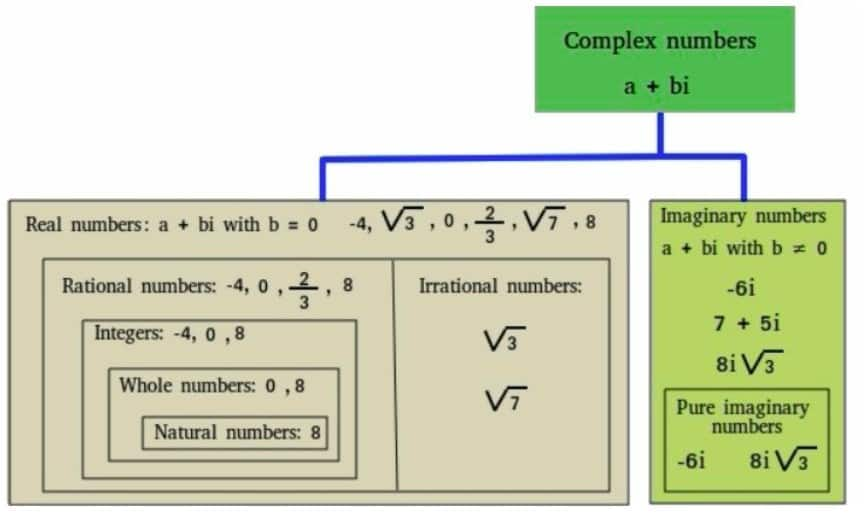
Complex Number

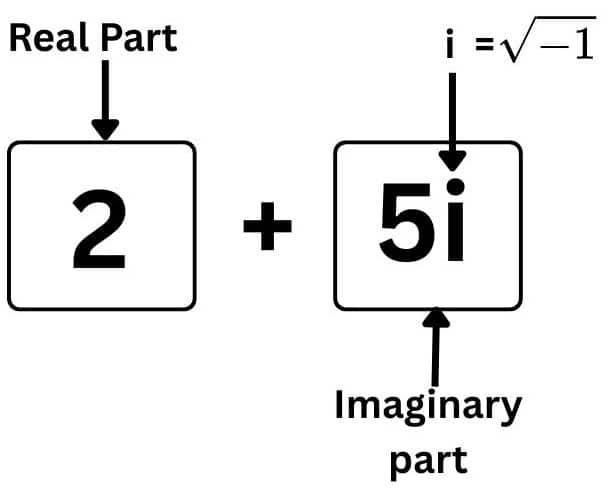
A complex number is defined as the combination of real and imaginary numbers.

Example: $3+4i$

Here, $3$ is real and $4i$ is the imaginary part.

Here is $i =\sqrt{(-1)}$, then we can say that $i^2 = -1$

Algebra Of Complex Numbers

Addition Of Two Complex Numbers

Let $x=a+ib$ and $y=c+id$

Therefore, $x+y= (a+c) +i(b+d)$

Properties

• The closure law: The sum of two complex numbers is also a complex number

• The commutative law $x+y=y+x$

• The associative law $(x+y)+z=x+(y+z)$

Difference Of Two Complex Numbers
Let $x=a+ib$ and $y=c+id$

Therefore $x-y= x+(-y)$

Multiplication of Two Complex Numbers
Let $x=a+ib$ and $y=c+id$

Therefore, $xy=ac-bd+i(ad+bc)$

Properties

• The closure law. The multiplication of two complex numbers is also a complex number

• The commutative law $xy=yx$

• The associative law $(xy)z=x(yz)$

• The distributive law $x(y+z) = xy+xz$ and $(x+y)z=xz+yz$

Division Of Two Complex Numbers

Let $x=a+ib$ and $y=c+id$

Therefore $\frac{x}{y}$ = $x.(\frac{1}{y})$

Power of $i$

In general, any integer k

$i^{4 k}=1, i^{4 k+1}=i, i^{4 k+2}=-1, i^{4 k+3}=-i$

The square roots of a negative real number

$i^2=-1, \text { and }(-i)^2=i^2=-1$

The Modulus And The Conjugate Of A Complex Number

If $x=a+i b$, then $|x|=\sqrt{a^2+b^2}$

Properties

1. $|x y|=|x||y|$

2. $|\frac{x}{y}|=\frac{|x|}{|y|}$

3. $(xy)'=x'y'$

4. $(x±y)’=x’±y’$

5. $(\frac{x}{y})’=\frac{x’}{y’}$

Argand Plane And Polar Representation

The complex number $a+ib$ corresponding to ordered pairs $(a, b)$ can also be represented geometrically in the XY plane.

In the Argand plane, the modulus of a complex number $a+ib =\sqrt{(a^2+b^2)}$ is the distance from the origin to the point.

Polar Representation Of A Complex Number

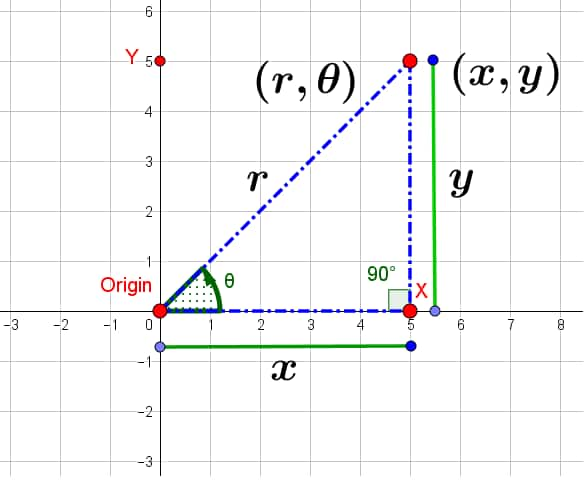
We note that the point P is uniquely determined by the ordered pair of real numbers $(r, θ)$ called the polar coordinates of the point P.

We get $a=r\cosθ, b=r\sinθ,$ thus $x=r(\cosθ +i \sin θ)$

Example:

Express the following in the form $\mathrm{a}+\mathrm{ib}: i^{-35}$
Solution : $i^{-35}=\frac{1}{i^{35}}=\frac{1}{\left(i^2\right)^{17} i}=\frac{1}{-i} × \frac{i}{i}=i$

Quadratic Equation

The equation that consists of the highest power in the polynomial is 2.

Let $ax^2+bx+c=0$ be a quadratic equation, then its discriminant is

$D=b^2-4ac$

Let us assume that $D<0$

Then $x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$

Example:

Solve $x^2+x+1=0$

Solution:

Here, $b^2-4ac=1^2-4×1×1=-3<0$

$\begin{aligned} & \text { Therefore } x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a} \\ &= \frac{-1 \pm \sqrt{1^2-4 × 1 × 1}}{2 × 1}=\frac{-1 \pm \sqrt{3} i}{2}\end{aligned}$

This concludes the Complex Numbers and Quadratic Equations class 11 notes.

Complex Numbers And Quadratic Equations: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 11 chapter 4 Complex Numbers And Quadratic Equations:

Question 1: If $\alpha$ is a root of the equation $x^2+x+1=0$ and $\sum_{\mathrm{k}=1}^{\mathrm{n}}\left(\alpha^{\mathrm{k}}+\frac{1}{\alpha^{\mathrm{k}}}\right)^2=20$, then n is equal to ______

Solution:
We have,
$\begin{aligned}
& \alpha=\omega \\
& \therefore\left(\omega^{\mathrm{k}}+\frac{1}{\omega^{\mathrm{k}}}\right)^2=\omega^{2 \mathrm{k}}+\frac{1}{\omega^{2 \mathrm{k}}}+2 \\
& =\omega^{2 \mathrm{k}}+\omega^{\mathrm{k}}+2 \quad \because \omega^{3 \mathrm{k}}=1
\end{aligned}$

$\begin{aligned}
& \therefore \sum_{k=1}^n\left(\omega^{2 k}+\omega^k+2\right)=20 \\
& \Rightarrow\left(\omega^2+\omega^4+\omega^6+\ldots+\omega^{2 n}\right)+\left(\omega+\omega^2+\omega^3+\ldots+\right. \\
& \left.\omega^n\right)+2 n=20
\end{aligned}$
Now if $n=3 m, \quad m \in I$
Then $0+0+2 \mathrm{n}=20 \Rightarrow \mathrm{n}=10$ (not satisfy) if $n=3 m+1$, then

$\begin{aligned}
& \omega^2+\omega+2 n=20 \\
& -1+2 n=20 \Rightarrow n=\frac{21}{2} \text { (not possible) } \\
& \text { if } n=3 m+2, \\
& \left(\omega^8+\omega^{10}\right)+\left(\omega^4+\omega^5\right)+2 n=20 \\
& \Rightarrow\left(\omega^2+\omega\right)+\left(\omega+\omega^2\right)+2 n=20 \\
& 2 n=22
\end{aligned}$
$\begin{aligned} & \mathrm{n}=11 \text { satisfy } \mathrm{n}=3 \mathrm{~m}+2 \\ & \therefore \mathrm{n}=11\end{aligned}$
Hence, the correct answer is 11.

Question 2: Consider the equation $\mathrm{x}^2+4 \mathrm{x}-\mathrm{n}=0$, where $\mathrm{n} \in[20,100]$ is a natural number. Then the number of all distinct values of n, for which the given equation has integral roots, is equal to

Solution:
Let us simplify the equation and solve for $x$,
$\begin{aligned}
& x^2+4 x+4=n+4 \\
& (x+2)^2=n+4 \\
& x=-2 \pm \sqrt{n+4} \\
& \because 20 \leq n \leq 100 \\
& \sqrt{24} \leq \sqrt{n+4} \leq \sqrt{104} \\
& \Rightarrow \sqrt{n+4} \in\{5,6,7,8,9,10\}
\end{aligned}$
$\therefore$ $6$ integral values of $n$ are possible.
Hence, the correct answer is $6$.

Question 3: Let $\mathrm{z} \in \mathrm{C}$ be such that $\frac{\mathrm{z}^2+3 \mathrm{i}}{\mathrm{z}-2+\mathrm{i}}=2+3 \mathrm{i}$. Then the sum of all possible values of $z^2$ is:

Solution:
Given:
$\frac{\mathrm{z}^2+3 \mathrm{i}}{\mathrm{z}-2+\mathrm{i}}=2+3 \mathrm{i}$
Apply cross multiplication,
$z^2+3 i=z(2+3 i)-7-4 i$
$z^2-z(2+3 i)+7+7 i=0$
Since it is quadratic, say it has two roots, $z_1,z_2$
$\begin{aligned} & z_1^2+z_2^2=\left(z_1+z_2\right)^2-2 z_1 z_2 \\ & =4-9+12 i-14-14 i \\ & =-19-2 i\end{aligned}$
Hence, the correct answer is $-19-2 \mathrm{i}$.

NCERT Class 11 Maths Notes – Chapter-Wise Links

For the convenience of students, Careers360 provides complete NCERT Class 11 Maths notes together in one location. Simply click the links below to access.

Subject-Wise NCERT Exemplar Solutions

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better understanding of the concepts.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

Students can also check these well-structured, subject-wise solutions.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and NCERT Syllabus

Before the start of a new academic year, students should refer to the latest syllabus to determine the chapters they’ll be studying. Below are the updated syllabus links, along with some recommended reference books.

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11