Conic Section Class 11th Notes - Free NCERT Class 11 Maths Chapter 11 notes - Download PDF

Conic Sections Class 11 Notes: Free PDF Download

Use the link below to download the Conic Sections Class 11 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 11 Chapter 10 Notes Conic Sections

A Conic section is the locus of a point in a plane so that its distance from a fixed point in the plane bears a constant ratio to its distance from a fixed line. The fixed point is called the focus of the Conic section, and the constant distance is called the directrix.

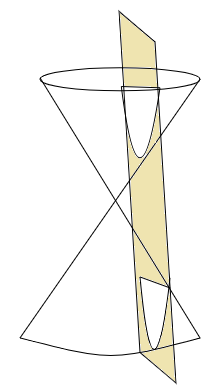
The Conic section can be obtained as sections of a right circular cone by a plane in various positions, and that is why they are called conic sections. A conic is given by a 2nd degree equation. Thus, a conic means a pair of straight lines, a circle, a parabola, an ellipse, or a hyperbola. A circle is a limiting case of an ellipse.

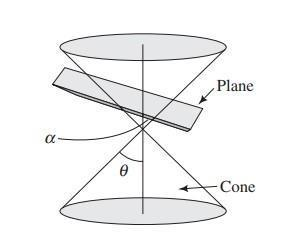
When the plane cuts the cone with a semi-vertical angle Ѳ at an angle α with the vertical axis of the cone, we have the following:

If α = 90°, the section is a circle.

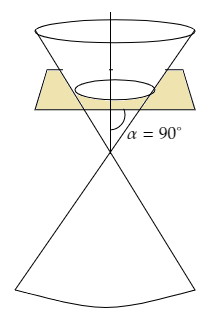
If Ѳ < α < 90°, the section is an ellipse.

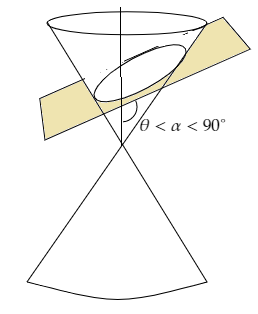
If α = Ѳ, the section is a parabola.

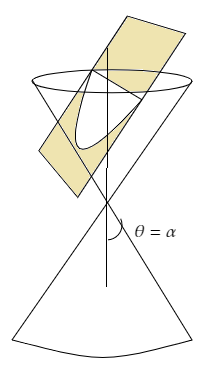
If 0 < α < Ѳ, the plane cuts through both sides of the cone, and the curve of intersection is a hyperbola.

Some Important Definitions to Remember

Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section.

Vertex: The point of intersection of the conic section and the axis is called the vertex of the conic section.

Double ordinate: Any chord that is perpendicular to the axis of the conic section is called a double ordinate of the conic section.

Focal chord: Any chord passing through the focus is called the focal chord of the conic section.

Focal distance: The distance between the focus and any point on the conic is known as the focal distance of that point.

Latus rectum: Any chord passing through the focus and perpendicular to the axis is known as the latus rectum of the conic section.

Equation of a Conic Section

The focus at $\mathrm{S}(\mathrm{h}, \mathrm{k})$ and the Directrix : $\mathrm{ax}+\mathrm{by}+\mathrm{c}=0$, then equation of conic

$
\begin{aligned}
& \Rightarrow P S=e \cdot P M \\
& \Rightarrow \sqrt{(x-h)^2+(y-k)^2}=e \cdot \frac{|a x+b y+c|}{\sqrt{a^2+b^2}} \\
& \Rightarrow(x-h)^2+(y-k)^2=e^2 \cdot \frac{(a x+b y+c)^2}{a^2+b^2}
\end{aligned}
$

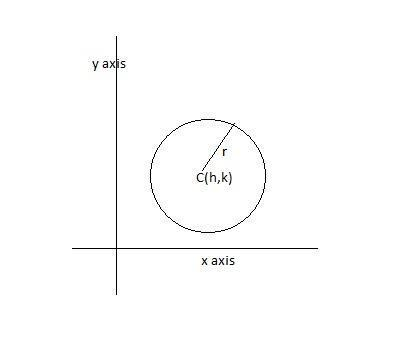
Equation Of A Circle Centre ($h, k$) and Radius $r$

Circle:

The distance of any point on the circumference of the circle from the centre is always constant, and the distance is known as the radius.

Assume that (h,k) is the radius of the circle, (x,y) is any point on the circumference of the circle, and r is the radius of the circle.

The distance between (h,k) and (x,y) is $\sqrt{(x-h)^2+(y-k)^2}$, which is the radius of the circle.

Thus, $\sqrt{(x-h)^2+(y-k)^2}=r$
Squaring both sides
$⇒(x-h)^2+(y-k)^2=r^2$

Standard Forms Of The Equation Of A Parabola

Parabola:

A parabola is a 2-dimensional plane shape, and it looks like a U shape.

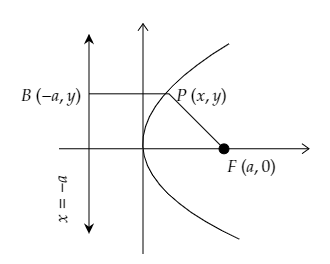
The distance between P and F is $\sqrt{(x-a)^2+(y-0)^2}$
The distance between B and P is $\sqrt{(x+a)^2+(y-y)^2}$
For a parabola, the lengths of PF and BP are equal.
So, $\sqrt{(x-a)^2+(y-0)^2}=\sqrt{(x+a)^2+(y-y)^2}$
Squaring both sides, we get,
$
\begin{aligned}
&⇒ (x-a)^2+(y-0)^2=(x+a)^2+(y-y)^2 \\
&⇒ x^2-2 a x+y^2=x^2+2 a x+a^2 \\
&⇒ y^2=4 a x
\end{aligned}
$
There are four possible cases of the parabola.

Case I

The axis of the parabola is along the x-axis, and the equation of the directrix is x+a = 0

The coordinate of the vertex is (0, 0).

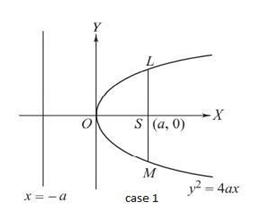
The distance between L and $\mathrm{S}=$ the distance of the directrix from the point L.
$\sqrt{(x-a)^2+(y-0)^2}=\left|\frac{x+a}{\sqrt{1^2}}\right|$
Squaring both sides, we get,
$
\begin{aligned}
&⇒ (x-a)^2+y^2=(x+a)^2 \\
&⇒ x^2-2 a x+a^2+y^2=x^2+2 a x+a^2 \\
&⇒ y^2=4 a x
\end{aligned}
$

Case II

The axis of the parabola is along the x-axis, and the equation of the directrix is x-a = 0.

The coordinate of the vertex is (0, 0).

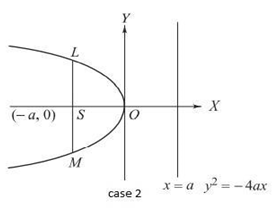
The distance between $L$ and $S=$ the distance of the directrix from the point $L$
$
\begin{aligned}
& \sqrt{(x+a)^2+(y-0)^2}=\left|\frac{x-a}{\sqrt{1^2}}\right| \\
&⇒ x^2+2 a x+a^2+y^2=x^2-2 a x+a^2 \\
&⇒ y^2=-4 a x
\end{aligned}
$

Case III

The axis of the parabola is along the y-axis, and the equation of the directrix is y+a = 0.

The coordinate of the vertex is (0,0).

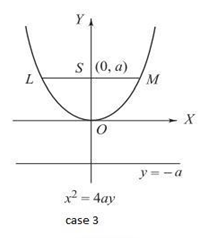
The distance between $L$ and $S=$ the distance of the directrix from the point $L$.
$
\begin{aligned}
& \sqrt{(x-0)^2+(y-a)^2}=\left|\frac{y+a}{\sqrt{1^2}}\right| \\
&⇒ x^2+y^2-2 a y+a^2=y^2+2 a y+a^2 \\
&⇒ x^2=4 a y
\end{aligned}
$

Case IV

The axis of the parabola is along the y-axis, and the equation of the directrix is y-a = 0.

The coordinate of the vertex is (0, 0).

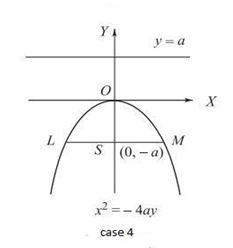
The distance between $L$ and $S=$ the distance of the directrix from the point $L$.
$
\begin{aligned}
& \sqrt{(x-0)^2+(y+a)^2}=\left|\frac{y-a}{\sqrt{1^2}}\right| \\
&⇒ x^2+y^2+2 a y+a^2=y^2-2 a y+a^2 \\
&⇒ x^2=-4 a y
\end{aligned}
$

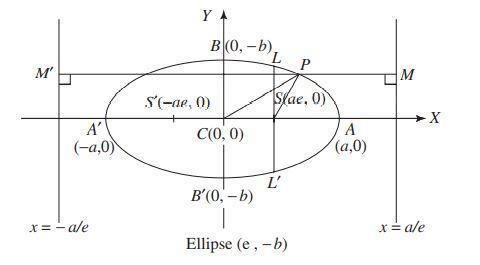
An Equation Of The Ellipse

Ellipse: It is a 2-dimensional shape in a plane. It has two foci and two directrices.

Major Axis: The length of the major axis is 2a. The coordinates of the endpoints of the major axis are (a,0) and (-a,0) when the major axis is along the x-axis.

Minor Axis: The length of the minor axis is 2b. The coordinates of the endpoints of the major axis are (0,b) and (0,-b) when the minor axis is along the y-axis.

Eccentricity: The ratio of the distance of the focus from the center of the ellipse and the distance of one end of the ellipse from the center of the ellipse. It is denoted by e.

The value of $e=\sqrt{1-\frac{b^2}{a^2}}$, where 2a is the length of the major axis and 2b is the length of the minor axis.

The eccentricity of an ellipse is less than 1.

The coordinates of the foci are (-ae,0) and (ae,0), where the major axis is along the x-axis, and the minor axis is the y-axis.

Latus rectum: Latus rectum is a line that is parallel to the directrix and passes through a focus. The length of the latus rectum is $\frac{2b^2} {a}$.

The general equation of an ellipse is $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.

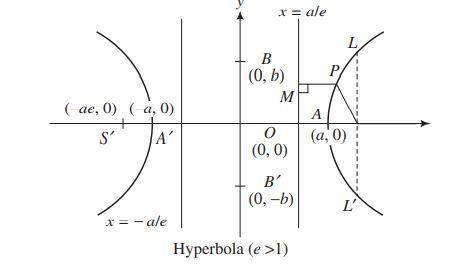
Equation Of The Hyperbola

Hyperbola: A Hyperbola is a 2-dimensional shape. A hyperbola has two foci and two directrices.

Major Axis: The length of the major axis is 2a.

Minor Axis: The length of the minor axis is 2b.

Vertex: A hyperbola has two vertices, and the coordinates of the vertices are (a,0) and (-a,0) when the major axis is along the x-axis.

Focus: The distance of any point on the hyperbola from a fixed point on the major axis and the distance of that of the hyperbola and directrix are always constant. The fixed point is known as the focus. The coordinates of the foci are (-ae,0) and (ae,0), where the major axis is along the x-axis, and the minor axis is the y-axis.

Eccentricity: The ratio of the distance of the focus from the centre of the ellipse and the distance of one end of the ellipse from the centre of the ellipse. It is denoted by e.

The value of $e=\sqrt{1+\frac{b^2}{a^2}}$, where 2a is the length of the major axis and 2b is the length of the minor axis. The eccentricity of a hyperbola is always greater than 1.

The general equation of a hyperbola is $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Conic Sections: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 11 chapter 10 Conic Sections:

Question 1: If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.

Solution:
Given lines are $6x-8y+8=0$ and $6x-8y-7=0$
These parallel lines are tangent to a circle
Diameter of circle = Distance between the lines
Diameter of circle = $\left |\frac{8-\left ( -7 \right )}{\sqrt{36+64}} \right |=\frac{15}{10}=\frac{3}{2}$
Radius of circle = $\frac{3}{4}$

Question 2: Find the equation of a circle concentric with the circle x² + y² – 6x + 12y + 15 = 0 and that has double its area.

Solution:
The given equation of the circle is :
x²+y²-6x+12y+15=0
(x-3)²+(y+6)²=(30)
Hence, centre is (3, -6) and radius is $\sqrt{30 }$
Since the required circle is concentric with the above circle, the centre of the required circle is (3, -6).
Let its radius be r
Area of circle = $\pi r^{2}=2\pi\left (\sqrt{30 } \right )^{2}$
⇒ $r^2 = 60$
⇒ $r = \sqrt{60}$
Equation of required circle $(x-3)^2+(y+6)^2=60$
⇒ $x^2+y^2-6x+12y-15 = 0$

Question 3: Find the equation of an ellipse whose eccentricity is $\frac{2}{3}$, latus rectum is 5, and the centre is (0, 0).

Solution:
Let the equation of the ellipse be $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$
$e=\frac{2}{3}$
Given that latus rectum $\frac{2b^{2}}{a}=5$
⇒ $b^{2}=\frac{5a}{2}=a^{2}\left ( 1-e^{2} \right )$
⇒ $\frac{5}{2}=a\left ( 1-\left ( \frac{2}{3} \right )^{2} \right )$
⇒ $a=\frac{9}{2}$
⇒ $b^{2}=\frac{45}{4}$
The required equation of the ellipse is $\frac{4x^{2}}{81}+\frac{4y^{2}}{45}=1$

Importance of NCERT Class 11 Maths Chapter 10 Notes

NCERT Class 11 Maths chapter 10 notes are a very competent revision material for students who aspire to achieve good marks in the Class 11 board exams, as well as in other competitive exams. Here are some reasons why students should read these notes.

• A strong base in conic sections will help students to deal with more complex topics like calculus, geometry and higher Mathematics. These notes will give students that conceptual clarity.
• These notes contain many images for the better visual representation of the concepts.
• The latest syllabus guidelines have been followed in these notes.
• Memorising these notes will give students better accuracy and speed during solving the questions.
• These notes are well structured and explained, made by teachers who have multiple years of experience in this field.
• These notes also contain the previous year’s questions, which students can check to identify common question types.

NCERT Class 11 Maths Notes – Chapter-Wise Links

All the links to chapter-wise notes for NCERT class 11 maths are given below:

Subject-Wise NCERT Exemplar Solutions

After completing the NCERT textbooks, students should practice exemplar exercises for a better understanding of the chapters and clarity. The following links will help students find exemplar exercises.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

Students can check the following links for more in-depth learning.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and NCERT Syllabus

Students should always check the latest NCERT syllabus before planning their study routine. Also, some reference books should be read after completing the textbook exercises. The following links will be very helpful for students for these purposes.

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11