A negative sign indicates that energy is being released from the system to the surroundings. For example, negative ΔH shows an exothermic reaction, and negative work or heat means the system is losing energy during the process.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 6 Thermodynamics
Have you ever thought how does the refrigerator work? Why do ice cubes melt without anyone touching them? Can energy be created, or is it always just transformed? NCERT Exemplar Class 11 Chemistry Solutions Chapter 6 Thermodynamics helps answer these questions by exploring the chemical and physical changes. These solutions provide a detailed explanation of some essential principles, such as the first law of thermodynamics, the second law of thermodynamics, and the concept of free energy, enthalpy, and work done in the processes and the principles and theories that govern their behaviour. This chapter also includes many key concepts such as energy transformations, heat, and work.
This Story also Contains
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: MCQ (Type 1)
- NCERT Exemplar Class 11 Chemistry Solutions chapter 6: MCQ (Type 2)
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: Short Answer Type
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: Matching Type
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: Assertion and Reason Type
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: Long Answer Type
- NCERT Class 11 Chemistry Chapter Thermodynamics: Higher Order Thinking Skills (HOTS) Questions
- Approach to Solve Questions of Chapter 6: Thermodynamics
- Topics and Subtopics Covered in the NCERT Textbook
- Advantages of Using Class 11 Chemistry Chapter 6 Thermodynamics NCERT Exemplar Solutions
- NCERT Exemplar Class 11 Chemistry Solutions Chapter-Wise
- Chapter Wise NCERT Solutions for Class 11 Chemistry
- NCERT Exemplar Class 11 Solutions
- NCERT Solutions subject-wise
- NCERT Notes subject-wise
- NCERT Books and NCERT Syllabus

The NCERT Exemplar Class 11 Chemistry solutions are designed by our subject eperts to offer a systematic and structured approach to these important concepts and help students to develop a clear understanding of critical concepts through the series of solved examples and conceptual explanations, these NCERT solutions provide a valuable resource to enhance performance in board exams as well as in the competitive exams like JEE Advanced, NEET, JEE Mains, etc. In this article, we will discuss detailed solutions to all the questions. Students can also check NCERT Exemplar Solutions for solutions to all questions, chapter-wise. This article includes some higher-order thinking skills (HOTS) questions that are beyond memorization and promote conceptual understanding, improve analytical thinking, enhance application skills, and build confidence in chemistry.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: MCQ (Type 1)
NCERT Exemplar Thermodynamics Class 11 Chemistry solutions for all the MCQ(Type-1) questions are given below. This chapter is very important from exam point of view and forms the basis for advanced topics.
Question:1 Thermodynamics is not concerned about.........
(i) energy changes involved in a chemical reaction.
(ii) the extent to which a chemical reaction proceeds.
(iii) the rate at which a reaction proceeds.
(iv) the feasibility of chemical reaction.
Answer:
The answer is option (iii) the rate at which a reaction proceeds.
Explanation: Thermodynamics is actually concerned with the initial and final states of a system and not with the rate at which the transformations take place. The laws can be applied to a system only when the system is in equilibrium.
Question:2 Which of the following statements is correct ?
(i) The presence of reacting species in a covered beaker is an example of open system.
(ii) There is an exchange of energy as well as matter between the system and the surroundings in a closed system.
(iii) The presence of reactants in a closed vessel made up of copper is an example of a closed system.
(iv) The presence of reactants in a thermos flask or any other closed insulated vessel is an example of a closed system.
Answer:
The answer is an option (iii) the presence of reactants in a closed vessel made up of copper is an example of a closed system.
Explanation: When the reactants are in a closed vessel, the matter cannot be exchanged. However, the energy may be exchanged through walls. So the reactants in a copper or a steel vessel are an example of a closed system.
Question:3 The state of gas can be described by quoting the relationship between _________ .
(i) pressure, volume, temperature
(ii) temperature, amount, pressure
(iii) amount, volume, temperature
(iv) pressure, volume, temperature, amount
Answer:
The answer is option (iv) pressure, volume, temperature, amount.
Explanation: The states of a gas can be described by the relationship between the variables such as p, V, T, and the amount of gas. These variables are called state variables. Their values are only concerned with the current state of the system.
Question:4 The volume of gas is reduced to half from its original volume. The specific heat will ________ .
(i) reduce to half
(ii) be doubled
(iii) remain constant
(iv) increase four times
Answer:
The answer is that option (iii) remains constant.
Explanation: The property of Specific heat capacity is an intensive property since it refers to the quantity of heat needed to elevate the temperature of one unit mass of a substance by one degree Celsius. It depends on the volume of the substance.
Question:5 During complete combustion of one mole of butane, 2658 kJ of heat is released. The thermochemical reaction for above change is
(i) $2C_{4}H_{10}(g)+13O_{2}(g)\rightarrow 8CO_{2}(g)+10H_{2}O_{(l)}\Delta _{c}H=-2658.0\; kJ\; mol^{-1}$
(ii) $C_{4}H_{10}(g)+\frac{13}{2}O_{2}(g)\rightarrow 4CO_{2}(g)+5H_{2}O(g)\Delta _{c}H=-1329.0\; kJ\; mol^{-1}$
(iii) $C_{4}H_{10}(g)+\frac{13}{2}O_{2}(g)\rightarrow 4CO_{2}(g)+5H_{2}O(l)\Delta _{c}H=-2658.0\; kJ\; mol^{-1}$
(iv) $C_{4}H_{10}(g)+\frac{13}{2}O_{2}(g)\rightarrow 4CO_{2}(g)+5H_{2}O(g)\Delta _{c}H=+2658.0 kJ\; mol^{-1}$
Answer:
The answer is the option (iii).
Explanation: The definition of the enthalpy of combustion is when the substance undergoes combustion and the enthalpy change that happens per mole in that substance. All other reactants are assumed to be in their standard states at that time.
Question:6 $\Delta _{f}U^{o}$ of formation of $CH_{4}(g)$ at a certain temperature is –393 kJ mol–1. The value of $\Delta _{f}H^{\ominus }$ is
(i) zero
(ii) $<\Delta _{f}U^{o}$
(iii) $>\Delta _{f}U^{o}$
(iv) equal to $\Delta _{f}U^{o}$
Answer:
The answer is option (ii) $<\Delta _{f}U^{o}$
Explanation: The reaction for the formation of $CH_{4}$ is:
$CH_{4}+2O_{2}\rightarrow CO_{2}+2H_{2}O$
$\Delta n_{g}=1-3=-2$
$\Delta H^{o}=\Delta U^{o}+\Delta n_{g}RT$
$\Delta n_{g}=-2$
Hence, $\Delta H^{o}<\Delta _{f}U^{o}$
Question:7 In an adiabatic process, no transfer of heat takes place between system and surroundings.Choose the correct option for free expansion of an ideal gas under adiabatic condition from the following.
(i) $q = 0, \Delta T \neq 0, w = 0$
(ii) $q \neq 0, \Delta T = 0, w = 0$
(iii) $q = 0, \Delta T = 0, w = 0$
(iv) $q = 0, \Delta T < 0, w \neq 0$
Answer:
The answer is option (iii) $q = 0, \Delta T = 0, w = 0$
Explanation: w =0 in the situation of free expansion since the volume is also constant. Also, q=0 considering the process is adiabatic. The first law of thermodynamics states that $\Delta U=q+w=0$ which is a constant.
Question:8 The pressure-volume work for an ideal gas can be calculated by using the expression
$w=-\int_{v_{i}}^{v_{f}}P_{ex}dV$
The work can also be calculated from the pV - plot by using the area under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (b) irreversibly from Vi to Vf, choose the correct option.
(i) w (reversible) = w (irreversible)
(ii) w (reversible) < w (irreversible)
(iii) w (reversible) > w (irreversible)
(iv) w (reversible) = w (irreversible) + pex. $\Delta V$
Answer:
Explanation: In the situation of irreversible compression, the area under the curve is always larger compared

Question:9 The entropy change can be calculated by using the expression $\Delta S = (q_{rev}/T)$.
When water freezes in a glass beaker, choose the correct statement amongst the following :
(i) $\Delta S$ (system) decreases, but $\Delta S$ (surroundings) remains the same.
(ii) $\Delta S$ (system) increases but $\Delta S$ (surroundings) decreases.
(iii) $\Delta S$ (system) decreases, but $\Delta S$ (surroundings) increases.
(iv) $\Delta S$ (system) decreases, and $\Delta S$ (surroundings) also decreases.
Answer:
The answer is option (iii) $\Delta S$ (system) decreases, but $\Delta S$ (surroundings) increases.
Explanation: As we all know in the case of an exothermic process, heat is released, which leads to a decrease in the surrounding entropy and as a result, the system entropy increases. As freezing is an exothermic process, we choose this option.
Question:10 On the basis of thermochemical equations (a), (b) and (c), find out which of the algebraic relationships given in options (i) to (iv) is correct.
(a) $C (graphite)+O_{2}(g)\rightarrow CO_{2}(g);\Delta _{r}H=x\; kJ\; mol^{-1}$
(b) $C (graphite)+\frac{1}{2}O_{2}(g)\rightarrow CO(g);\Delta _{r}H=y\; kJ\; mol^{-1}$
(c) $CO _{(g)} + \frac{1}{2}O_{2(g)}\rightarrow CO_{2(g)} ; \Delta _{r}H= z\; kJ\; mol^{-1}$
(i) z = x + y
(ii) x = y – z
(iii) x = y + z
(iv) y = 2z – x
Answer:
The answer is option (iii) x = y + z
x =y + z is the correct option as the Algebraic sum of y and z will give x.
Explanation: When y is subtracted from x, we get z. Explained below:
$C (graphite)+O_{2}(g)\rightarrow CO_{2}(g);\Delta _{r}H=x\; kJ\; mol^{-1}$________(i)
$C (graphite)+\frac{1}{2}O_{2}(g)\rightarrow CO(g);\Delta _{r}H=y\; kJ\; mol^{-1}$________(ii)
When subtracted, we receive:
$CO _{(g)} + \frac{1}{2}O_{2(g)}\rightarrow CO_{2(g)} ; \Delta _{r}H= z\; kJ\; mol^{-1}$________(iii)
So, z= x-y, or, easily put, x=y+z. Hence, option c.
Question:11 Consider the reactions given below. On the basis of these reactions find out which of the algebraic relations given in options (i) to (iv) is correct?
(i) $C(g) + 4H(g) \rightarrow CH_{4}(g); \Delta _{r}H=x\; kJ \; mol^{-1}$
(ii)
$C(graphite, s) + 2H_{2}(g) \rightarrow CH_{4}(g); \Delta _{r}H = y \; kJ \; mol ^{-1}$
(i) x = y
(ii) x = 2y
(iii) x >y
(iv) x< y
Answer:
The answer is option (iii).
Explanation: In the case of reaction b, the bonds are broken, but in reaction a, the bonds are not broken. However, the same bonds are formed in both cases.
Question:12 The enthalpies of elements in their standard states are taken as zero. The enthalpy of formation of a compound
(i) is always negative
(ii) is always positive
(iii) may be positive or negative
(iv) is never negative
Answer:
The answer is option (iii) maybe positive or negative
Explanation: It can be positive or negative as the reaction could be exothermic or endothermic.
Question:13 Enthalpy of sublimation of a substance is equal to
(i) enthalpy of fusion + enthalpy of vaporization
(ii) enthalpy of fusion
(iii) enthalpy of vaporization
(iv) twice the enthalpy of vapourization.
Answer:
The answer is an option (i) enthalpy of fusion + enthalpy of vaporization
Explanation: In the case of enthalpy of sublimation, a solid converts to liquid and then to gas. In this process, the conversion to liquid requires enthalpy of fusion and the conversion to vapor requires the enthalpy of vapourisation.
Question:14 Which of the following is not correct?
(i) $\Delta G$ is zero for a reversible reaction.
(ii) $\Delta G$ is positive for a spontaneous reaction
(iii) $\Delta G$ is negative for a spontaneous reaction
(iv) $\Delta G$ is positive for a non-spontaneous reaction.
Answer:
The answer is option (ii) $\Delta G$ is positive for a spontaneous reaction
Explanation: As we all know for a spontaneous reaction, $\Delta G$ is always negative.
NCERT Exemplar Class 11 Chemistry Solutions chapter 6: MCQ (Type 2)
NCERT Class 11 Thermodynamics Chemistry exemplar solutions for all the MCQ (Type-2) questions are given below. The chapter is vast yet easy to learn.
Question:15 Thermodynamics mainly deals with
(i) interrelation of various forms of energy and their transformation from one form to another.
(ii) energy changes in the processes which depend only on the initial and final states of the microscopic system containing a few molecules.
(iii) how and at what rate these energy transformations are carried out.
(iv) the system in an equilibrium state or moving from one equilibrium state to another equilibrium state.
Answer:
The answer is option (i) and (iv)
Explanation: The prerequisite conditions required for the thermodynamics laws to be applicable is for the system to be in equilibrium. Also, they are relevant to the macroscopic systems and not to the microscopic systems which have very few numbers of molecules.
Question:16 In an exothermic reaction, heat is evolved, and the system loses heat to the surroundings. For such system
(i) $q_{p}$ will be negative
(ii) $\Delta _{r}H$ will be negative
(iii) $q_{p}$ will be positive
(iv) $\Delta _{r}H$ will be positive.
Answer:
The answer is options (i) and (ii)
Explanation: In an exothermic reaction, the heat is released to the surroundings of the system. So,$q_{p}$ and $\Delta _{r}H$ will be negative.
Question:17 The spontaneity means, having the potential to proceed without the assistance of an external agency. The processes which occur spontaneously are
(i) flow of heat from colder to warmer body.
(ii) gas in a container contracting into one comer.
(iii) gas expanding to fill the available volume.
(iv) burning carbon in oxygen to give carbon dioxide.
Answer:
The answer is options (iii) and (iv).
Explanation: Both the processes, namely, the filling of empty space by gas, as well as the burning of carbon which leads to the formation of carbon dioxide, are spontaneous processes.
Question:18 For an ideal gas, the work of reversible expansion under isothermal conditions can be calculated by using the expression $w = -nRT$ In $V_{f} / V_{i}$
A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversibly to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively. Choose the correct option.
(i) Work done at 600 K is 20 times the work done at 300 K.
(ii) Work done at 300 K is twice the work done at 600 K
(iii) Work done at 600 K is twice the work done at 300 K.
(iv) $\Delta U=0$ in both cases.
Answer:
The answer is (iii) and (iv).
Explanation: Now, q = -w, in the case of an isothermal reversible change
$Q=-w=nRT\; In\frac{vf}{vi}$
$\frac{w(600k)}{w(300k)}=\frac{1\times R\times 600k\; In\frac{10}{1}}{1\times R\times 300K\; In\frac{10}{1}}=2$
In case of ideal gases, $\Delta U = 0$ for the expansion, which is isothermal. There is no change in the internal energy as the temperature is constant, and, hence $\Delta U = 0$.
Question:19 Consider the following reaction between zinc and oxygen and choose the correct options out of the options given below:
$2Zn(s) + O_{2}(g) \rightarrow 2ZnO(s); \Delta H=-693.8 \; kJ \; mol^{-1}$
(i) The enthalpy of two moles $ZnO$ is less than the total enthalpy of two moles of $Zn$ and one mole of oxygen by 693.8 kJ.
(ii) The enthalpy of two moles of $ZnO$ is more than the total enthalpy of two moles of $Zn$ and one mole of oxygen by 693.8 kJ.
(iii) 8 kJ mol -1 energy is evolved in the reaction.
(iv) 693.8 kJ mol-1 energy is absorbed in the reaction.
Answer:
The answers are options (i) and (iii).
Explanation:
$\Delta _{f}H=\sum _{i}a_{i}\Delta _{f}H-\sum _{i}b_{i}\Delta _{f}H$
The reaction depicted above is exothermic in nature, and, hence, the reactant enthalpy is more than the product enthalpy.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: Short Answer Type
Short answer type questions from Chapter 6 Thermodynamics NCERT Exemplar Solutions Class 11 Chemistry for all the short-answer type questions are given below:
1 mol of water or 18g of water has an enthalpy of change for vaporization. Now it is given that the change of enthalpy required for 1 mole of water is 40.79 kJ/mol.
For 2 moles of water, the enthalpy change will be 2 x 40.79 = 81.58 KJ. Therefore the standard enthalpy of vaporisation of water is $\Delta _{vap} H = 40.79\; kJ / mol$
Question:21 One mole of acetone requires less heat to vaporise than 1 mol of water. Which of the two liquids has a higher enthalpy of vapourization?
Answer:
Water has a greater enthalpy of vaporization than acetone. Acetone molecules have a weak force of attraction between them, and hence they require less heat to break the molecular bonds.
No, since CaCO3 has been formed from other compounds and not from its constituent elements.
Question:23 The value of $\Delta _{f}H^{\ominus }$ for $NH_{3}$ is – 91.8 kJ mol–1. Calculate the enthalpy change for the following reaction :
$2NH_{3}(g) \rightarrow N_{2}(g) + 3H_{2}(g)$
Answer:
The enthalpy change for the given reaction can be calculated as: -
$N_{2}(g) + 3H_{2}(g) \rightarrow 2NH_{3} (g)$
$\Delta _{f} H = -91.8\; kg/mol$
The enthalpy of the reaction is +91.8 kg/mol. This happens as with the reversal of reaction, the value of$\Delta _{r} H$ also gets reversed.
According to Hess’s law, $\Delta _{r} H = \Delta _{r} H_{1} + \Delta _{r} H_{2} +\Delta _{r} H_{3}.....$
This is so because, during the reaction $A\rightarrow B$, B’s formation undergoes various intermediate reactions, with the overall value of the enthalpy being $\Delta _{r}H$.
Question:25 The enthalpy of atomisation for the reaction $CH_{4}(g)\rightarrow C(g) + 4H (g)\; is \; 1665 \; kJ mol^{-1}$. What is the bond energy of $C-H$ bond?
Answer:
The reaction presented in the question is
$CH_{4}(g)\rightarrow C(g) + 4H (g)$
Now, $\Delta _{a} H = 1665 \; kJ / mol^{-1}$
The mean bond enthalpy of the C-H bond should be used here. For the atomization of 4 moles of C-H bonds, the value is 1665 kJ/mol-1 So, per mole energy = 1665/4 = 416.2 kJ / mol-1
In order to calculate the lattice enthalpy of NaBr,
(i)$Na(s) \rightarrow Na(g) ; \Delta _{sub}H^{\circ } =108.4\; kJ mol^{-1}$
(ii) $Na\rightarrow Na^{+} + e^{-} ; \Delta _{i}H^{\circ } = 496\; kJ mol^{-1}$
(iii) $\frac{1}{2}Br_{2}\rightarrow Br, \frac{1}{2}\Delta_{diss} H^{\circ } =96\; kJ\; mol^{-1}$
(iv)$Br+e^{-}\rightarrow Br^{-};\Delta egH^{\circ } = - 325 kJ\; mol^{-1}$
$\Delta _{f} H^{\circ } = \Delta _{sub} H^{\circ } + \frac{1}{2}\Delta _{diss}H^{\circ }+ \Delta _{i}H^{\circ } + \Delta _{eg}H^{\circ } + \Delta _{latttice}H^{\circ }$
$\Delta _{latttice}H^{\circ } = -360.1 -108.4-96-496+325 = -735.5KJ mol^{-1}$
Question:27 Given that $\Delta H = 0$ for mixing of two gases. Explain whether the diffusion of these gases into each other in a closed container is a spontaneous process or not?
Answer:
Entropy in an isolated system increases with the increase in the disorder in the system. As diffusion is a spontaneous process, the process also will be a spontaneous one.
Temperature and the entropy change are both inversely proportional quantities. Q and T are related to the entropy in the case of reversible reaction in the following manner:
$\Delta S=q_{rev}/T$
Yes. The temperature of the surroundings and the system will be identical when we look at the condition of thermal equilibrium. The enthalpy varies in an inversely proportionate manner in the case of system and surroundings. If the enthalpy of the system increases, the enthalpy of the surroundings deceases.
Question:30 At 298 K, Kp for the reaction $N_{2}O_{4}(g)\rightleftharpoons 2NO_{2} (g)$ is 0.98. Predict whether the reaction is spontaneous or not.
Answer:
As per the information given in the question, Kp for the above reaction is 0.98
$\Delta _{y}G = \Delta _{y}H- T \Delta _{y}G = -RT\; ln K$
For a process to be of spontaneous nature, $\Delta G$ should be negative
As $\Delta_{y} G=-RT\; ln K_{p}$
Hence $\Delta_{y} G$ has a negative connotation, and the reaction given is of a spontaneous nature
In case of a cyclic change, the value of $\Delta H = 0$ i.e. there is not going to be any change in the enthalpy.
Question:32 The standard molar entropy of $H_{2}O(l)$ is 70 J K-1 mol-1. Will the standard molar entropy of $H_{2}O$(s) be more, or less than 70 J K-1 mol-1?
Answer:
The standard molar entropy of H2O (s) will be less than 70 JK-1mol-1. This is because entropy decreases when ice is formed from water as molecules reduce their movement and are arranged in an orderly fashion.
Question:33 Identify the state functions and path functions out of the following: enthalpy, entropy, heat, temperature, work, fand ree energy.
Answer:
Out of the options mentioned, the state functions are: Temperature, Enthalpy, Entropy, and Free energy and the path functions are Work, Heat, etc.
Question:34 The molar enthalpy of vapourization of acetone is less than that of water. Why?
Answer:
As the intermolecular forces of attraction is lower in acetone than in water, the enthalpy of vaporization of water is higher than that of acetone.
Question:35 Which quantity out of $\Delta _{r}G$ and $\Delta _{r}G^{\circleddash }$ will be zero at equilibrium?
Answer:
$\Delta _{r}G$ will always be zero.
$\Delta _{r}G^{\circleddash }$ is zero for K = 1 because $\Delta _{r}G^{\circleddash }$= – RT lnK, $\Delta _{r}G^{\circleddash }$ will be non zero for other values of K.
Question:36 Predict the change in internal energy for an isolated system at constant volume.
Answer:
There is no change in internal energy for an isolated system at a constant volume if there is no transfer of heat as work which are the conditions of an isolated system. Hence, $\Delta H=0$.
Question:37 Although heat is a path function heat absorbed by the system under certain specific conditions is independent of the path. What are those conditions? Explain.
Answer:
The conditions in which heat becomes path-independent are:
a) when the volume remains the same
$\Delta V=0,so\; \Delta U=q+p\; \Delta V=q$
As $\Delta U$ is a state function, q is also a state function.
b) when the pressure remains the same
$\Delta U=q-p\; \Delta V$
So, $q=p\; \Delta V+\Delta U=\Delta H$ which is a state function
So, at a constant volume and at constant pressure heat change is a state function because it is equal to a change in internal energy and a change in enthalpy respectively which are state functions.
A free expansion is known as the expansion of gas in a vacuum. The equation can be written as
$(-w)=p(V_{2}-V_{1})=0\times (5-1)=0$
q =0, when we consider isothermal expansion.
Referring to the first law of thermodynamics we have
$q=\Delta U+(-w)$
$0=\Delta U+0$
Hence, $\Delta U=0$
Question:39 Heat capacity $(C_{p})$ is an extensive property but specific heat (c) is an intensive property. What will be the relation between $(C_{p})$ and c for 1 mol of water?
Answer:
The quantity of heat needed to raise the temperature of one mole of the substance by one degree Celsius is known as its heat capacity.
For the molar heat capacity calculation, we multiply 18 and the value of the specific heat
$C_{p}=18\times c$
We know that, C (specific heat) = $4.18\; J\; g^{-1}K^{-1}$ Heat capacity,
Therefore, $C_{p}=18\times 4.18\; JK^{1}=75.24\; JK^{-1}$
In the case of an ideal gas, the difference between $C_{p}\; and \; C_{v}$ is nR, where n represents the number of moles and R is the universal gas constant.
Therefore, for 10 moles of an ideal gas-
$C_{p} - C_{v}= 10\; R$
$C_{p} - C_{v}= 10 \times 4.18\; J$
= 41.84 J
Question:41 If the combustion of 1g of graphite produces 20.7 kJ of heat, what will be the molar enthalpy change? Give the significance of the sign also.
Answer:
We know that, 1 mole of carbon = 12g
To calculate the molar enthalpy, change of graphite, we need to multiply enthalpy change for 1g carbon along with its molar mass. Which as per the information provided in the question can be calculated as,
$- 20.7 \times 12 = -248.4 \; kJ mol^{-1}$ (negative sign depicts exothermic reaction as there is heath involved)
We know that to calculate Enthalpy change, the formula is
= (Bond energy of H-H bond + Br-Br bond) – (2 × bond energy of H-Br)
In our case, we can calculate enthalpy change by substituting the values.
= $(435 + 192) kJ mol^{-1} - (2 \times 368) kJ mol^{-1}$
= -109 kJ mol-1
As per the information provided in the question, for one mole of $CCl_{4} (154 g)$, the heat of vaporization required is 30.5 kJ/mol.
Hence for the vaporisation of 284 g of $CCl_{4}$, we require:
$= \frac{284 \; g}{154 \; g \; mol^{-1}} \times 30.5\; kJ\; mol^{-1}$
$=56.2\; kJ$
Standard molar enthalpy of formation is the enthalpy change for the formation of one mole of a compound from its most stable states or reference states. As per the given information in the question, the standard enthalpy for the given equation is – 572 kJ mol–1
Now the enthalpy of formation for $H_{2}O$ will be half the enthalpy of the value in the given equation. So, now we can calculate that:
$\Delta _{f}H=\frac{1}{2}\times \Delta _{y}H=-\frac{52}{2}=-286\; kJ\; mol^{-1}$
Assumption: The cylinder is filled with one mole of gas, and the piston is frictionless. Let the pressure of the gas inside be p and the volume of gas be $V_{I}$.
A piston is moved towards the inside to make the external pressure $(P_{ext})$ equal to p. Now, let us assume that this change takes place in a single step; hence, V is the final volume. The work done by the piston is depicted in the graph shown below by shading the area.
$P_{ext}\Delta V=AV_{I}(or\; BV_{II})\times (V_{I}-V_{II})$
Question:46 How will you calculate work done on an ideal gas in a compression, when change in pressure is carried out in infinite steps?
Answer:
When a process can be reversed by making an extremely small change in it, we call it a reversible process. The pressure-volume graph can be used to calculate the work done. The pressure is not constant, and changes in infinitesimal amounts as compression happens from the initial volume Vi to the final volume Vf. The graph below depicts the work done with the shaded area.
(a) Throwing a stone from the ground to the roof
b) the reaction involved is a process where the energy decreases after the reaction. It can be represented as:
In process b), potential energy/enthalpy change is contributing factor to the spontaneity.
Question:48 Enthalpy diagram for a particular reaction is given in Fig. 6.3. Is it possible to decide the spontaneity of a reaction from given diagram? Explain.
Answer:
No, for the state of spontaneity, the enthalpy change is not the only criteria. Entropy also needs to be taken into account here.
Question:49 1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.
Answer:
We can conclude from the figure that this change is a reversible change.
Now,
$W=-2.303\; nRT\; log\; p1/p2$
$= -2.303 \times 1 \times 8.314 \times 298 \times log \; 2$
$= -2.303 \times 8.314 \times 298 \times 0.3010\; J$
$=-1717.46\; J$
We know that the amount of work done =$-p_{ext}\Delta V$
On substituting the values in the formula, we get,
$-2\; bar\times (50-10)L=-80\; L\; bar$
According to the described problem,$1L\; Bar = 100\; J$
Therefore, $-80\; L\; bar=(-80\times 100)=-8000\; J$
$=-8\; kJ,$ which is the amount of work done
The significance of the negative sign states that the work is done on the surroundings of the system. In the case of reversible expansion, the work done will be more.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: Matching Type
NCERT Exemplar Thermodynamics Class 11 Chemistry solutions for all the matching type questions are given below. These are generally asked in exams to test your knowledge. These exemplar solutions is quite helpful for competitive exams.
Question:51 Match the following:
|
A |
B |
|
(i) Adiabatic Process |
(a) Heat |
|
(ii) Isolated system |
(b) At constant volume |
|
(iii) Isothermal change |
(c) First law of thermodynamics |
|
(iv) Path function |
(d) No exchange of energy and matter |
|
(v) State function |
(e) No transfer of heat |
|
(vi) $\Delta U=q$ |
(f) Constant temperature |
|
(vii)Law of conservation of energy |
(g) Internal energy |
|
(viii) Reversible process |
(h)$P_{ext}=0$ |
|
(ix) Free Expansion |
(i) At constant pressure |
|
(x) $\Delta H=q$ |
(j) Infinitely slow process which |
|
(xi) Intensive property |
(k) Entropy |
|
(xii) Extensive property |
(l) Pressure |
|
|
(m) Specific heat |
Answer:
(i) - (e); (ii)- (d); (iii)- (f); (iv)- (a); (v)- (g), (k), (l); (vi)- (b); (vii)- (c); (viii)- (j); (ix) (h); (x)- (i); (xi)- (a), (l), (m); (xii)- (g), (k)
Question:52 Match the following processes with entropy change:
|
Reaction |
Entropy change |
|
(i) A liquid vapourises |
(a) $\Delta S = 0$ |
|
(ii)Reaction is non-spontaneous at all temperatures and $\Delta H$ is positive |
(b) $\Delta S =$ Positive |
|
(iii) Reversible expansion of an ideal gas |
$\Delta S =$ negative |
Answer:
(i) - b
(ii) - c
(iii) -a
Explanation:
|
Reaction |
Entropy change |
|
(i) A liquid vaporizes |
As a liquid changes to a gaseous state, the movement of molecules will increase and hence the entropy will also increase. |
|
ii) Reaction is non-spontaneous at all temperatures and AH is positive. |
ΔG is positive as the process in non-spontaneous. Also, ΔH is positive. Hence, ΔS is negative. |
|
(iii) Reversible expansion of an ideal |
This process at every stage is always in equilibrium |
Question:53 Match the following :
|
$\Delta$(Parameters) $\Delta _{r}H^{\ominus }$ $\Delta _{r}S^{\ominus }$ $\Delta _{r}G^{\ominus }$ |
Description |
|
(i) $+\; \; \; \; \; \; \; -\; \; \; \; \; \; \; +$ |
(a) Non-spontaneous at high temperature. |
|
(ii) $-\; \; \; \; \; \; \; -\; \; \; \; \; \; \; +at\; high\; T$ |
(b) Spontaneous at all temperatures |
|
(iii) $-\; \; \; \; \; \; \; +\; \; \; \; \; \; \; -$ |
(c) Non-spontaneous at all temperatures |
Answer:
(i) - c
(ii) - a
(iii) -b
Explanation:
|
Parameters $\Delta _{r}H^{\ominus }$ $\Delta _{r}S^{\ominus }$ $\Delta _{r}G^{\ominus }$ |
Description |
|
i) + - + |
ΔG is positive, and ΔS is negative when we have a positive enthalpy change. So, at all temperatures, the process remains non-spontaneous |
|
ii) - - + at a hight T |
when we have a positive enthalpy change, ΔG is positive. The process will be non-spontaneous at high temperatures. |
|
iii) - + - |
When enthalpy change is negative, ΔG is negative, and ΔS is positive. Hence the process will be spontaneous at all temperatures. |
Question:54 Match the following :
|
(i) Entropy of vapourization |
(a) decreases |
|
(ii) K for spontaneous process |
(b) is always positive |
|
(iii) Crystalline solid state |
(c) lowest entropy |
|
(iv) $\Delta U$ in adiabatic expansion of ideal gas |
(d) $\frac{\Delta H_{vap}}{T_{b}}$ |
Answer:
(i) - b, d
(ii) - b
(iii) -c
(iv) -a
Explanation:
|
Column I |
Column II |
|
(i) Entropy of vaporization |
ΔH vap / T |
|
(ii) K for spontaneous process |
$Since\; \; \Delta ,G^{\ominus}=\Delta , H^{\ominus}-T\Delta ,S^{\ominus}=-RT$ |
|
(iii) Crystalline solid state |
Molecules in the solid state of matter are the most stable and ordered and hence have the least entropy |
|
(iv) ΔU in adiabatic expansion of ideal gas |
ΔU decreases as in the situation of expansion, the system is the one that does work. so, q =0 and ΔU = -w |
NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: Assertion and Reason Type
The Assertion and Reason type questions of Chapter 6 test a students conceptual clarity and logical reasoning skills. These Thermodynamics Class 11 NCERT Exemplar solutions help you understand the reason behind concepts of Thermodynamics.
Question:55 In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): Combustion of all organic compounds is an exothermic reaction.
Reason (R) : The enthalpies of all elements in their standard state are zero.
(i) Both A and R are true and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true but R is false.
(iv) A is false, but R is true.
Answer:
The answer is option (ii) Both A and R are true, but R is not the correct explanation of A.
Explanation: The reactant enthalpies are always greater than the product enthalpies when it comes to the combustion reaction.
Question:56 In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A) : Spontaneous process is an irreversible process and may be reversed by some external agency.
Reason (R) : Decrease in enthalpy is a contributory factor for spontaneity.
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false.
(iv) A is false, but R is true.
Answer:
The answer is option (ii) Both A and R are true, but R is not the correct explanation of A.
Explanation: In the case of a spontaneous process, the randomness should be positive, and ΔU should be negative.
Question:57 In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): A liquid crystallizes into a solid and is accompanied by a decrease in entropy.
Reason (R): In crystals, molecules organize in an ordered manner.
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false.
(iv) A is false, but R is true.
Answer:
The answer is option (i) Both A and R are true, and R is the correct explanation of A.
Explanation: As the liquid starts to crystallize the randomness in the molecules decreases as they get arranged in an orderly fashion. Hence, the entropy decreases.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 6: Long Answer Type
The Long Answer Type questions of Chapter 6 test a students conceptual clarity and logical reasoning skills. These Thermodynamics Class 11 NCERT Exemplar solutions help you understand the concepts of Thermodynamics.
Question:58 Derive the relationship between $\Delta H$ and $\Delta U$ for an ideal gas. Explain each term involved in the equation.
Answer:
Now, the heat absorbed at constant volume is equal to the change in the internal Energy.
$\Delta U = q_{p} - p\; \Delta V$
qp is the heat absorbed.
p $\Delta V$ is the expansion work done by the system
the equation can be represented as $U_2 - U_1 = p (V_2 - V_1)$
so, we get,
$q_{p} = (U_2 + Pv_2) - (U_1 + Pv_1) ----------------- (1)$
now we take into consideration, the enthalpy
$H = U + pV -------------------------- (2)$
Hence, we can rewrite the first equation as,
$q_{p} = H_2 - H_1 = \Delta H$
now, in the case of the state functions.
H is a state function because it depends on U, p, and V, all of which are state functions.
So, $\Delta H$, as well as qp, is path independent.
We can rewrite equation 2 in case of finite changes as,
$\Delta H = \Delta U + p\Delta V --------------------- (3)$
We measure changes in enthalpy, when heat is being absorbed at a constant pressure.
ΔV = 0, for constant volume. So, equation 3 becomes ΔH = ΔU = qv
Let Va be the total volume of gaseous reactants and Vb be the total volume of gaseous products. Let nA be the number of moles of gas reactants and nB be the number of moles for the gaseous products. The ideal gas law is:
pVa= nA R T
pVb= nB R T
now,
pVb - pVa = (nB - nA) RT
hence,
$p\Delta V = \Delta n_g RT ------------------- (4)$
now, by using equation 3 and equation 4,
we can write
ΔH = ΔU + Δng RT
Extensive properties Mass, internal energy, heat capacity.
Intensive properties Pressure, molar heat capacity, density, mole fraction, specific heat, temperature and molarity.
Ratio of two extensive properties is always intensive.
Extensive/Extensive = Intensive
So, mole fraction and molarity are intensive properties.
When one mole of an ionic compound dissociates into its ions, the enthalpy change related to this process is called lattice enthalpy.
$Na^{+} Cl^{-}\rightarrow Na^{+} + Cl^{-}$
$\Delta H_{lattice}= 788 kJ/mol$
Lattice enthalpy for NaCl is calculated as follows:
1) Sublimation of sodium metal
$Na(s)\rightarrow Na(g)$
2) Ionization enthalpy: ionization of sodium atoms
$Na(g)\rightarrow Na^{+}(g)+e^{-1}(g)$
3) Bond dissociation enthalpy: dissociation of chlorine
$\frac{1}{2}Cl_{2}(g)\rightarrow Cl^{-}(g)$
4) Electron gain enthalpy: electron gain by chlorine
$Cl^{-}(g)+e^{-1}(g)\rightarrow Cl(g)$
$5)Na^{+}(g)+Cl^{-}(g)\rightarrow Na^{+}Cl^{-}(s)$
These steps collectively form the BORN-HABER Cycle, wherein the sum total of enthalpy changes around a cycle is equal to 0.
We are aware of the equation that,
$\Delta S_{tot}=\Delta S_{sys}+\Delta S_{surr}$
The temperature of the system and surroundings will be equal if both are in equilibrium. Also, the enthalpy changes are inversely proportional in both of them.
We can represent the entropy changes in the surroundings as:
$\Delta S_{Surr}=\Delta H_{surr}/T=-(\Delta H_{sys}/T)$
$\Delta S_{tot}=\Delta S_{sys}-(\Delta H_{sys}/T)$
Hence, we can rewrite this as:
$T\Delta S_{tot}=T\Delta S_{sys}- \Delta H_{sys}$
In case of a spontaneous process:
$-(\Delta H_{sys}-T\Delta S_{sys})>0,since \Delta S _{tot}>0$
We can write the above equation as:
$-\Delta G > 0$
$\Delta G = \Delta H - T \Delta S > 0$
ΔG is the measure of free energy as it is the net available energy for performing some useful work.
Criteria for spontaneity:
$\Delta G < 0$: spontaneous process
$\Delta G > 0$: non-spontaneous process
Let us assume that a cylinder has 1-mole gas without any weight or friction having area of cross-section A. Hence, the total volume is depicted by Vi and the initial pressure is assumed to be p.
Let us assume that pext is the external pressure.
Now, if pext> p, the piston moves down until pext = p,
Hence, the final volume is Vf and the distance moved by piston be $\Delta$l
Thus,$\Delta$V = $\Delta$l × A (eq-1)
$\Delta$V = Vf - Vi
We know that, force = pressure ×area
Therefore, F = pext× A (eq-2)
If w is work done on the system
W = force × displacement
= pext × A ×$\Delta$l
From eq-1
W = pext×($\Delta$V)
W = -pext$\Delta$V
W = -pext( vf – vi)
If vf> vi work is done by the system and w is negative. If vf< vi work is on the system and w is positive
NCERT Class 11 Chemistry Chapter Thermodynamics: Higher Order Thinking Skills (HOTS) Questions
Some higher-order thinking skills questions with solutions based on the NCERT Exemplar Class 11 Chemistry Solutions Chapter 6 Thermodynamics are given below:
Question 1: Total enthalpy change for freezing of 1 mol of water at $10^{\circ} \mathrm{C}$ to ice at $-10^{\circ} \mathrm{C}$ is $\qquad$
(Given : $\Delta_{\mathrm{fus}} \mathrm{H}=\mathrm{x} \mathrm{kJ} / \mathrm{mol}$
$\begin{aligned}
& \mathrm{C}_{\mathrm{p}}\left[\mathrm{H}_2 \mathrm{O}(\mathrm{l})\right]=\mathrm{y} \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1} \\
& \mathrm{C}_{\mathrm{p}}\left[\mathrm{H}_2 \mathrm{O}(\mathrm{~s})\right]=\mathrm{z} \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}
\end{aligned}$
- $-x-10 y-10 z$
- $-10(100 x+y+z)$
- $10(100 x+y+z)$
- $x-10 y-10 z$
Answer

$\Delta H=1 \times y(0-10)-x \times 1000+1 \times z\left(-10^{\circ}-0^{\circ}\right)$
$\Delta H=-(10 y+10 z-1000 x) \mathrm{J}$
$\Delta H=-10(100 x+y+z)$ Joule.
Hence, the correct answer is option (2).
Question 2: Which of the following mixing of 1 M base and 1 M acid leads to the largest increase in temperature?
- 30 mL HCl and 30 mL NaOH
- $30 \mathrm{~mL} \mathrm{CH}_3 \mathrm{COOH}$ and 30 mL NaOH
- 50 mL HCl and 20 mL NaOH
- $45 \mathrm{~mL} \mathrm{CH}_3 \mathrm{COOH}$ and 25 mL NaOH
Answer:
The higher the number of milli moles of acid or base reacted higher will be temperature rise.
Option (4) $n_{\text {acid }}$ or $n_{\text {base }}$ reacted $=30 \mathrm{~m} \mathrm{~mol}$
Option (2) $n_{\text {acid }}$ or $n_{\text {base }}$ reacted $=30 \mathrm{~m} \mathrm{~mol}$
but less energy will be released by neutralisation reaction of weak acid hence option (2) can not be correct.
Option (3) $\Rightarrow 20 \mathrm{~m} \mathrm{~mol}$
Option (4) $\Rightarrow 25 \mathrm{~m} \mathrm{~mol}$
Hence, the correct answer is option (1)
Question 3. Calculate the entropy change when 10 moles of an ideal gas expand reversibly and isothermally from an initial volume of 10 litres to 100 litres at 300 K.
Answer:
Step 1: Use the ideal gas law to relate the initial and final conditions.
$
\mathrm{PV}=\mathrm{nRT}
$
Step 2: Calculate the initial and final pressures using the ideal gas law.
$
\mathrm{P}_1=\frac{\mathrm{nRT}}{\mathrm{~V}_1}
$
$
\mathrm{P}_2=\frac{\mathrm{nRT}_2}{\mathrm{~V}_2}
$
Given: Number of moles, $\mathrm{n}=10$ moles Initial volume, $\mathrm{V}_1=10$ liters Final volume, $\mathrm{V}_2=100$ liters Temperature, $\mathrm{T}=300 \mathrm{~K}$ Gas constant, $\mathrm{R}=8.314 \mathrm{~J} /(\mathrm{mol} \cdot \mathrm{K})$
Step 3: Use the isothermal process to find the change in volume $(\Delta \mathrm{V})$ and the work done $(\mathrm{W})$
$
\Delta V=V_2-V_1
$
Step 4: Calculate the work done $(\mathrm{W})$ using the external pressure ( $\mathrm{P}_{\text {ext }}$ ).
$
\mathrm{W}=-\mathrm{P}_{\mathrm{ext}} \cdot \Delta \mathrm{~V}
$
Since the process is isothermal, the external pressure is equal to the gas pressure at all times:
$
P_{\mathrm{ext}}=\mathrm{P}_1=\frac{\mathrm{nRT}_1}{V_1}
$
Step 5: Use the definition of entropy change $(\Delta \mathrm{S})_{\text {for an isothermal process: }}$
$
\Delta \mathrm{S}=-\frac{\mathrm{W}}{\mathrm{~T}}
$
Step 6: Substitute the values and calculate the entropy change.
$
\Delta S=-\frac{-P_{\mathrm{ext}} \cdot \Delta V}{T}
$
Calculating the numerical value of the entropy change:
$
\Delta \mathrm{S}=-\frac{-\left(\frac{\mathrm{nRT}}{\mathrm{~V}_1}\right) \cdot\left(\mathrm{V}_2-\mathrm{V}_1\right)}{\mathrm{T}}
$
Substitute the given values:
$
\Delta \mathrm{S}=-\frac{-\left(\frac{(10 \mathrm{~mol}) \cdot(8.314 \mathrm{~J} /(\mathrm{mol}-\mathrm{K})) \cdot(300 \mathrm{~K})}{10 \mathrm{~L}}\right) \cdot(100 \mathrm{~L}-10 \mathrm{~L})}{300 \mathrm{~K}}
$
Calculating the numerical value of the entropy change:
$
\Delta \mathrm{S} \approx 276.93 \mathrm{~J} / \mathrm{K}
$
So, the entropy change when 10 moles of an ideal gas expand reversibly and isothermally from an initial volume of 10 litres to 100 litres at 300 K is approximately $276.93 \mathrm{~J} / \mathrm{K}$.
Hence, the answer is ($276.93 \mathrm{~J} / \mathrm{K}$).
Question 4: A given mass of gas expands from the state $A$ to the state $B$ by three path 1,2 and 3 as shown in the figure. If $W_1, W_2$ and $W_3$ as respectively be the magnitudes work done by the gas along three paths then:
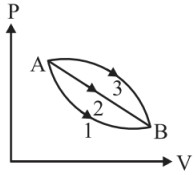
(1) $\quad W_1>W_2>W_3$
(2) $\quad W_1<W_2<W_3$
(3) $\quad W_1=W_2=W_3$
(4) $\quad W_2<W_3<W_1$
Answer:
Work done $=$ Area under the curve.
W1 area under the curve $<\mathrm{W}_ 2<\mathrm{W} _3$
Hence, the correct answer is option (2).
Question 5: The correct statement amongst the following is :
(1) The term 'standard state' implies that the temperature is $0^{\circ} \mathrm{C}$
(2) The standard state of pure gas is the pure gas at a pressure of 1 bar and temperature 273 K
(3) $\boldsymbol{\Delta}_{\mathrm{f}} \mathrm{H}_{298}^{\boldsymbol{\theta}}$ is zero for $\mathrm{O}(\mathrm{g})$
(4) $\boldsymbol{\Delta}_{\mathrm{f}} \mathrm{H}_{298}^{\boldsymbol{\theta}}$ is zero for $\mathrm{O}_2(\mathrm{~g})$
Answer:
Option (1)
It asserts that the term "standard state" implies that the temperature is $0^{\circ} \mathrm{C}(273 \mathrm{~K})$.
In fact, "standard state" typically specifies a standard pressure (1 bar) and a chosen temperature-commonly 298 K for tabulated thermodynamic data-not necessarily $0^{\circ} \mathrm{C}$.
Thus, Option 1 is incorrect.
Option (2)
It claims that the standard state for a pure gas is defined at 1 bar and 273 K .
In modern thermochemistry, the standard state generally means the pure substance at 1 bar, but the standard temperature most commonly used is $298 \mathrm{~K}\left(25^{\circ} \mathrm{C}\right)$, not 273 K $\left(0^{\circ} \mathrm{C}\right)$.
Thus, Option 2 is incorrect.
Option (3)
It claims that $\Delta_f H_{298}^{\circ}$ is zero for $O(g)$ (atomic oxygen).
However, the standard state of oxygen is diatomic $O_2(g)$, not atomic oxygen. Since $O(g)$ is not the most stable form of oxygen under standard conditions, its formation enthalpy is not zero.
Hence, Option 3 is incorrect.
Option (4)
$\Delta_{\mathrm{f}} \mathrm{H}_{298}^0$ for $\mathrm{O}_2$ is zero and not for O.
The standard enthalpy of formation of any element in its most stable form is zero, regardless of temperature (though typically reported at 298 K ).
Thus, option (4) is correct
Hence, the correct answer is option (4).
Approach to Solve Questions of Chapter 6: Thermodynamics
Thermodynamics deals with the energy changes in physical and chemical processes. It’s a concept-based chapter that requires a good grasp of definitions, laws, formulas, and logical application. Sometimes problems seem very difficult, but once we understand the basic rules and strategy, it becomes very easy to solve all the questions related to that particular topic. The basic understanding of how to solve questions from the Thermodynamics Class 11 NCERT is essential for building a strong foundation in physical chemistry. The approaches given below help students in developing the right techniques to solve questions.
1. Learning about the basic concepts like system, surrounding, internal energy, work, heat, enthalpy and Laws of Thermodynamics is very important for solving questions. These topics also help in understanding energy changes in chemical reactions and predicting the direction of physical and chemical change.
2). Before solving any question, first give it a thorough reading and note down all the information given in the question. Identify given data like pressure, volume, temperature, etc. and what we need to find.
3). Using the correct formula is very important for Solving NCERT Class 11 Chemistry Chapter 5 Thermodynamics questions
(i). Internal Energy Change
$\Delta U=U_{\text {final }}-U_{\text {initial }}$
(ii). First Law of Thermodynamics
$\Delta U=q+W$
(iii). Work Done in Expansion/Compression
$W=-P \Delta V$
(iv). Enthalpy and Enthalpy Change
$H=U+P V$
$\Delta H=\Delta U+P \Delta V$
(v). tandard Enthalpy Change of Reaction
$\Delta H_{\text {reaction }}^{\circ}=\sum \Delta H_{\text {products }}^{\circ}-\sum \Delta H_{\text {reactants }}^{\circ}$
(vi). Gibbs Free Energy
$\Delta G=\Delta H-T \Delta S$
4). Be careful while dealing with units and convert them if necessary to ensure consistency like temperature in Kelvin or volume in litres, etc.
5). Practice again and again, as it will help in mastering thermodynamics numerically.
- Start with simpler problems
- Then gradually move to ones involving concepts like enthalpy change, work in isothermal or adiabatic processes, and heat capacity.
6). Chapter 6 Thermodynamics Questions from the NCERT books are asked directly in the boards and other competitive exams. Do previous year questions from NEET and JEE to get used to question patterns.
Topics and Subtopics Covered in the NCERT Textbook
All the topics and subtopics included in the Class 11 Chemistry Chapter 6 Thermodynamics are listed below:
- Thermodynamics Terms
- The System and the Surroundings
- Types of the System
- The State of the System
- The Internal Energy as a State Function
- Applications
- Work
- Measurement of $\Delta U$ and $\Delta H$: Calorimetry
- Enthalpy Change, $\Delta H$ of a Reaction – Reaction Enthalpy
- Enthalpies for Different Types of Reactions
- Spontaneity
- Gibbs Energy Change and Equilibrium
Advantages of Using Class 11 Chemistry Chapter 6 Thermodynamics NCERT Exemplar Solutions
NCERT Exemplar Thermodynamics Class 11 Chemistry solutions helps students understand the basic concepts from the NCERT book in a simple and organised manner. The advantages of using these solutions are given below:
- These solutions are designed to help students understand the basic concepts like internal energy, enthalpy, and Gibbs free energy, laws of thermodynamics, heat capacity, enthalpy changes, and spontaneity of reactions with the help of solved examples.
- Using these NCERT exemplar class 11 solutions helps students to revise formulas, definitions, and laws.
- The class 11 chemistry chapter 6 thermodynamics question answers are prepared by subject experts in a very comprehensive and clear manner.
- They provide step by step explanation of every question of NCERT.
NCERT Exemplar Class 11 Chemistry Solutions Chapter-Wise
Besides NCERT Exemplar Class 11 Chemistry Solutions Chapter 6 Thermodynamics, chapter-wise exemplar solutions are given below:
Chapter Wise NCERT Solutions for Class 11 Chemistry
Chapter-wise NCERT Solutions for Class 11 Chemistry are carefully prepared to help students understand fundamental concepts with clarity. These solutions strictly follow the latest NCERT syllabus and CBSE guidelines, ensuring accurate and reliable answers for every exercise question.
NCERT Exemplar Class 11 Solutions
NCERT subject-wise exemplar solutions are given below:
NCERT Solutions subject-wise
NCERT Solutions are designed to help students understand concepts clearly and prepare effectively for exams. These solutions based on the latest NCERT curriculum and follow CBSE guidelines.
NCERT Notes subject-wise
NCERT Notes provide concise and well-structured explanations of all important topics as prescribed in the NCERT syllabus. Given below are links for Class 11 NCERT Notes
NCERT Books and NCERT Syllabus
NCERT Books and the NCERT Syllabus form the foundation of the CBSE curriculum and play a crucial role in academic learning. Given below are links for Class 11 NCERT Books and Syllabus
Frequently Asked Questions (FAQs)
Temperature is a measure of the average kinetic energy of particles in a substance and significantly affects thermodynamic processes. It influences reaction rates, equilibrium positions, and the amount of energy available for work.
Chapter 6 Thermodynamics NCERT Exemplar Solutions Class 11 Chemistry is important because it forms the foundation for understanding energy changes in physical and chemical processes. It helps students interpret reaction feasibility, calculate heat and work, and apply thermodynamic laws—concepts essential for higher-level chemistry and competitive exams.
To prepare class 11 chemistry chapter 6 thermodynamics question answers focus on understanding key concepts such as system, surroundings, enthalpy, internal energy, and Gibbs free energy. Practise numerical problems regularly, revise thermodynamic laws carefully, and solve NCERT and Exemplar questions to strengthen conceptual clarity.
Exothermic reactions release heat into the surroundings. So the surroundings become warmer while Endothermic reactions absorb heat from the surroundings. So the surroundings become cooler.
NCERT Class 11 Chemistry Chapter 6 Thermodynamics questions provide detailed, step-by-step answers to advanced questions on thermodynamics.
The three laws of Thermodynamics are given below:
- Zeroth Law: If two systems are in thermal equilibrium with a third, they are in thermal equilibrium with each other.
- First Law: Energy can be transferred or changed from one form to another, but it cannot be created or destroyed.
- Second Law: The total entropy of an isolated system cannot decrease over time.
Thermodynamics in chemistry is the study of energy changes that occur in chemical reactions and physical processes. It deals with heat, work, energy, and the relationships between them.
Reversible processes can be reversed, and both the system and surroundings return to their original state, while irreversible processes can not be reversed, and the system and surroundings do not return to their original state
Spontaneity refers to the natural tendency of a process to occur on its own, without any external intervention.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters










