Theclass 11 chemistry chapter 7 equilibrium ncert exemplar solutions provide clear, detailed answers to advanced questions on chemical and ionic equilibrium. They help students understand concepts like reversible reactions, equilibrium constants, Le Chatelier’s principle, and ionic product of water, improving their conceptual clarity and exam preparation.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 7 Equilibrium
Why chemical reactions didn’t always go to completion but instead decided to settle halfway, how the human body maintains a constant pH level despite changes that occur every day? The answer to all these questions lies in NCERT Exemplar Class 11 Chemistry Chapter 7 Equilibrium. It is a fundamental concept in chemistry that describes the state in which the rate of the forward reaction equals the rate of the reverse reaction that results in no overall change in the concentration of reactants and products.
This Story also Contains
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: MCQ (Type 1)
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: MCQ (Type 2)
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: Short Answer Type
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: Matching Type
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: Assertion and Reason Type
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: Long Answer Type
- Class 11 Chemistry NCERT Chapter Equilibrium: Higher Order Thinking Skills (HOTS) Questions
- Approach to Solve Questions of Chapter 7 Equilibrium
- Topics of NCERT Exemplar class 11 Chemistry Equilibrium
- Important Formulas of Chapter 7 Equilibrium
- Advantages of Using Class 11 Chemistry Chapter 7 Equilibrium NCERT Exemplar Solutions
- NCERT Exemplar Class 11 Chemistry Solutions Chapter-Wise
- NCERT Solutions for Class 11 Chemistry Chapter-wise
- NCERT Exemplar Class 11 Solutions
- NCERT Solutions subject-wise
- NCERT Notes subject-wise
- NCERT Books and NCERT Syllabus

NCERT Exemplar Solution are designed in such a way that the students can build a strong foundation in chemistry. These NCERT Exemplar solutions for class 11 chemistry provide thorough explanations of the problems, helping students to apply theoretical concepts effectively. Students can enhance their problem-solving skills and gain clarity on balancing chemical equations and equilibrium constants by practicing these NCERT Solutions.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: MCQ (Type 1)
The NCERT Exemplar Class 11 Chemistry Solutions Chapter 7 Equilibrium MCQ questions are given below. This chapter is very important from exam point of view.
Question 1. We know that the relationship between $K_{c}$ and $K_{p}$ is
$K_{p}$ $= K_{c}(RT)^{\Delta n}$
What would be the value of $\Delta n$ for the reaction $NH_{4}Cl(s) \leftrightharpoons NH_{3}(g) + HCl(g)$
(i) 1
(ii) 0.5
(iii) 1.5
(iv) 2
Answer:
The answer is option (iv) 2
Explanation: Because,
$\Delta n$= Number of moles of product - Number of moles of reactant.
$=2-0$
$=2$
Question 2. For the reaction $H_{2}(g) + I_{2}(g) \rightleftharpoons 2HI(g)$ the standard free energy is $\Delta G^{\circleddash }>0.$ The equilibrium constant (K) would be,
(i) K = 0
(ii) K > l
(iii) K = 1
(iv) K < 1
Answer:
The answer is option (iv) K < 1
Explanation: As $\Delta G^{\Theta }=-RT$ lnK and so if $\Delta G^{\Theta }>0$, then $-\Delta G^{\Theta }/RT$ is negative, which means K<1. This certainly implies that a non-spontaneous reaction or a reaction proceeds in the forward direction to such a small degree that only a very small quantity of product is formed.
Question 3. Which of the following is not a general characteristic of equilibria involving physical processes?
(i) Equilibrium is possible only in a closed system at a given temperature.
(ii) All measurable properties of the system remain constant.
(iii) All the physical processes stop at equilibrium.
(iv) The opposing processes occur at the same rate, and there is a dynamic but stable condition.
Answer:
The answer is option (iii). All the physical processes stop at equilibrium.
Explanation: What happens at equilibrium is that both processes occur at the same rate, and thus there is a dynamic but pretty much stable condition. Thus, no further physical processes occur.
Question 4. $PCl_{5}$ , $PCl_{3}$ and $Cl_{2}$ are at equilibrium at 500 K in a closed container and their concentrations are $0.8\times 10^{-3}\; mol\; L^{-1}$ , $1.2 \times 10^{-3} mol L^{-1}$ and $1.2 \times 10^{-3} mol L^{-1}$ respectively. The value of $Kc$ for the reaction PCl5 (g) $\rightleftharpoons$PCl3 (g) + Cl2 (g) will be
(i) $1.8\times 10^{3}mol\; L^{-1}$
(ii) $1.8\times 10^{-3}$ mol L-1
(iii) $1.8\times 10^{-3}\; Lmol^{-1}$
(iv) $0.55\times 10^{4}$
Answer:
The answer is the option (ii) $1.8\times 10^{-3}$ mol L-1
Explanation :
$K_{c}=\frac{[PCl_{3}][Cl_{2}]}{[PCl_{5}]}=\frac{1.2\times 10^{-3}\times 1.2\times 10^{-3}}{0.8\times 10^{-3}}$
$=1.8\times 10^{-3}\; mol\; L^{-1}$
Question 5. Which of the following statements is incorrect?
(i) In equilibrium mixture of ice and water kept in perfectly insulated flask mass of ice and water does not change with time.
(ii) The intensity of red colour increases when oxalic acid is added to a solution containing iron (III) nitrate and potassium thiocyanate.
(iii) On the addition of a catalyst, the equilibrium constant value is not affected,
(iv) The equilibrium constant for a reaction with a negative ΔH value decreases as the temperature increases.
Answer:
Ans. (ii) The intensity of red colour increases when oxalic acid is added to a solution containing iron (III) nitrate and potassium thiocyanate.
Explanation: Oxalic Acid which is $H_{2}C_{2}O_{4}$ reacts with the $Fe^{3+}$ ions forming a stable complexion that is $[Fe(C_{2}O_{4})_{3}]^{3-}$ thereby decreasing the concentration of free $Fe^{3+}$ ions and because of which concentration of $[Fe(SCN)]^{2+}$ decreases and thus the intensity of red colour decreases.
Question 6. When hydrochloric acid is added to cobalt nitrate solution at room temperature, the following reaction takes place, and the reaction mixture becomes blue. On cooling the mixture, it becomes pink. On the basis of this information mark the correct answer.
$[Co(H_{2}O)_{6}]^{3+} (aq) + 4Cl^{-}(aq) \rightleftharpoons [CoCl_{4}]^{2-}(aq) + 6H_{2}O(l)$
(i) ΔH > 0 for the reaction
(ii) ΔH < 0 for the reaction
(iii) ΔH = 0 for the reaction
(iv) The sign of ΔH cannot be predicted on the basis of this information.
Answer:
(i) $\Delta H > 0$ for the reaction
Explanation: On the cooling of the mixture, the reaction tends to move towards the backward direction, which is an endothermic reaction, and, hence, $\Delta H > 0$.
Question 7. The pH of neutral water at 25°C is 7.0. As the temperature increases, ionisation of water increases, however, the concentration of H+ ions and OH- ions are equal. What will be the pH of pure water at 60°C?
(i) Equal to 7.0
(ii) Greater than 7.0
(iii) Less than 7.0
(iv) Equal to zero
Answer:
The answer is option (iii) Less than 7.0
Explanation: Kw increases $[H+ ][OH- ]>10^{-14}$
$As [H+ ]=[OH- ]$
$or [H+ ]^{2} =10^{-14}$
$or [H+ ]>10^{-7} M$
$pH< 7$
Question 8. The ionisation constant of an acid, Ka, is the measure of the strength of an acid. The Ka values of acetic acid, hypochlorous acid and formic acid are $1.74\times 10^{-5}, 3.0\times 10^{-8}$ and $1.8\times 10^{-4}$ respectively. Which of the following orders of pH of 0.1 mol dm-3 solutions of these acids is correct?
(i) acetic acid > hypochlorous acid > formic acid
(ii) hypochlorous acid > acetic acid > formic acid
(iii) formic acid > hypochlorous acid > acetic acid
(iv) formic acid > acetic acid > hypochlorous acid
Answer:
The answer is the option (iv) formic acid > acetic acid > hypochlorous acid
Explanation: Higher the value of Ka higher will be the acidic strength.
$1.8\times 10^{-4} > 1.74\times 10^{-5} > 3.0\times 10^{-8}$
Question 9. $K_{a1},$ , $K_{a2},$ $K_{a3}$ are the respective ionisation constants for the following reactions.
$H_{2}S \rightleftharpoons H^{+} + HS^{-}$
$HS^{-} \rightleftharpoons H^{+} + S^{2-}$
$H_{2}S \rightleftharpoons 2H^{+} + S^{2-}$
The correct relationship between $K_{a1},$ , $K_{a2},$ $K_{a3}$ is
(i) $K_{a3} = K_{a1} \times K_{a2}$
(ii) $K_{a3} = K_{a1} + K_{a2}$
(iii) $K_{a3} = K_{a1} - K_{a2}$
(iv) $K_{a3} = \frac{K_{a1} }{K_{a2}}$
Answer:
The answer is the option (i) $K_{a3} = K_{a1} \times K_{a2}$
Explanation:
$K_{a1}=\frac{[H^{+}][HS^{-}]}{[H_{2}S]}.....(1)$
$K_{a2}=\frac{[H^{+}]+[S^{2-}]}{[HS]}.....(2)$
On adding equation (i.e. multiplication of equilibrium constants) 1 and 2, we get,
$K_{a3}=\frac{[H^{+}]^{2}[S^{2-}]}{[H_{2}S]}$
Which proves that for a dibasic acid $K_{a3} = K_{a1} \times K_{a2}$
Question 10. The acidity of BF3 can be explained on the basis of which of the following concepts?
(i) Arrhenius concept
(ii) Bronsted Lowry concept
(iii) Lewis concept
(iv) Bronsted Lowry as well as Lewis concept.
Answer:
The answer is the option (iii) Lewis concept
Explanation: All Lewis Acids can accept a pair of electrons and hence they can be called be electron-deficient species and so BF3 is a Lewis acid.
Question 11. Which of the following will produce a buffer solution when mixed in equal volumes?
(i) $0.1 mol\; dm^{-3} NH_{4}OH \; and\; 0.1\; mol \; dm^{-3} HCl$
(ii) $0.05 \; mol\; dm^{-3} NH_{4}OH \; and\; 0.1\; mol \; dm^{-3} HCl$
(iii) $0.1 \; mol\; dm^{-3} NH_{4}OH \; and\; 0.05\; mol \; dm^{-3} HCl$
(iv) $0.1 \; mol\; dm^{-3} \;CH_{3}COONa \; and\; 0.1\; mol \; dm^{-3} NaOH$
Answer:
The answer is the option (iii) $0.1 \; mol\; dm^{-3} NH_{4}OH \; and\; 0.05\; mol \; dm^{-3} HCl$
Explanation: A mixture of ammonium chloride and ammonium hydroxide acts as a buffer.
Question 12. In which of the following solvents is silver chloride most soluble?
(i) $0.1\; mol\; dm^{-3}\; AgNO3\; solution$
(ii) $0.1 \; mol \; dm^{-3} HCl \: solution$
(iii) $H_{2}O$
(iv) Aqueous ammonia
Answer:
The answer is the option (iv) Aqueous ammonia
Explanation: Aqueous ammonia absorbs chloride ions, and thus the equilibria will have to shift in the forward direction and thus the solubility of silver chloride increases.
Question 13. What will be the value of pH of 0.01 mol dm-3 $CH_{3}COOH(K_{a}=1.74\times 10^{-5})$
(i) 3.4
(ii) 3.6
(iii) 3.9
(iv) 3.0
Answer:
The answer is the option (i) 3.4
Explanation: We know that the ionization of $CH_{3}COOH$ occurs as follows: -
$CH_{3}COOH+H_{2}O\leftrightharpoons H_{3}O^{+}+CH_{3}COO^{-}$
Now, we know that the initial concentration: 0.01
We also know that the euilibrium concentration: 0.01 – x x x
Now, the ionization constant $K_{a}=\frac{[H_{3}O^{+}][CH^{3}COO^{-}]}{[CH_{3}COOH]}=\frac{x^{2}}{0.01-x}$
$As, x>>0.01 \; Therefore, 0.01 - \times \sim 0.01 .$
$X^{2}=1.74\times 10^{-5}\times 0.01$
$X = 4.2 \times 10^{-4}$
Which can also be written as, $pH = -log (4.2 \times 10^{-4} ) = 3.4$
Question 14. Ka for $CH_{3}COOH$ is $1.8\times 10^{-5}$ and $K_{b}$ , for $NH_{4}OH$ is $1.8\times 10^{-5}$ . The pH of ammonium acetate will be
(i) 7.005
(ii) 4.75
(iii) 7.0
(iv) Between 6 and 7
Answer:
The answer is the option (iii) 7.0
Explanation: The formation of ammonium acetate is formed by a weak base $NH_{4}OH \; and \; CH_{3}COOH.$
We know that in case of salts with weak acids,
$pH = \frac{1}{2} [pKw + pKa - pKb ]$
In this case,
$= \frac{1}{2} [14 - log (1.8 \times 10-5) + log (1.8 \times 10-5 )]$
$=7$
Question 15. Which of the following options will be correct for the stage of half completion of the reaction $A\rightleftharpoons B$?
(i) $\Delta G^{\Theta } =0$
(ii) $\Delta G^{\Theta } >0$
(iii) $\Delta G^{\Theta } <0$
(iv) $\Delta G^{\Theta } =-RT\; In\; 2$
Answer:
The answer is the option (i)$\Delta G^{\Theta } =0$
Explanation: At the stage of half completion of reaction the two concentrations rae equal, [A] = [B]. Therefore, K = 1.
Question 16. On increasing the pressure, in which direction will the gas-phase reaction proceed to re-establish equilibrium, is predicted by applying Le Chatelier’s principle. Consider the reaction.
$N_{2}(g) + 3H_{2}(g) \rightleftharpoons 2NH_{3}(g)$
Which of the following is correct, if the total pressure at which the equilibrium is established, is increased without changing the temperature?
(i) K will remain the same
(ii) K will decrease
(iii) K will increase
(iv) K will increase initially and decrease when pressure is very high
Answer:
The answer is the option (i) K will remain the same
Explanation: If the temperature is not changed, equilibrium constant K will remain the same.
Question 17. What will be the correct order of vapour pressure of water, acetone and ether at 30°C? Given that among these compounds, water has a maximum boiling point and ether has a minimum boiling point?
(i) Water < ether < acetone
(ii) Water < acetone < ether
(iii) Ether < acetone < water
(iv) Acetone < ether < water
Answer:
The answer is the option (ii) Water < acetone < ether
Explanation: More will be the boiling point, and less will be the vapour pressure.
Question 18. At 500 K, the equilibrium constant, Kc, for the following reaction is 5.
$\frac{1}{2} H_{2} (g) + \frac{1}{2} I_{2} (g) \rightleftharpoons HI (g)$
What would be the equilibrium constant $K_{c}$ for the reaction
$2HI (g)\rightleftharpoons H_{2} (g) + I_{2} (g)$
(i) 0.04
(ii) 0.4
(iii) 25
(iv) 2.5
Answer:
The answer is the option (i) 0.04
Explanation: If the given equation is multiplied by 2, the equilibrium constant for the new equation will be squared, and on reversing the reaction the value of the equilibrium constant is reciprocated. Thus
$K=5_{2}=25$
For the required reaction equation $K=\frac{1}{25}=0.04$
Question 19. In which of the following reactions, the equilibrium remains unaffected on the addition of a small amount of argon at constant volume?
(i) $H_{2}(g)+I_{2}(g)\leftrightharpoons 2HI(g)$
(ii) $PCl_{5}(g)\leftrightharpoons PCl_{3}(g)+ Cl_{2}(g)$
(iii) $N_{2}(g)+3H_{2}(g)\leftrightharpoons 2NH_{3}(g)$
(iv) The equilibrium will remain unaffected in all three cases.
Answer:
The answer is the option (iv) The equilibrium will remain unaffected in all three cases.
Explanation: At constant volume, equilibrium remains unaffected even on the addition of inert gas.
In each of the other cases,
(i) $H_{2}(g)+I_{2}(g)\leftrightharpoons 2HI(g)$
(ii) $PCl_{5}(g)\leftrightharpoons PCl_{3}(g)+ Cl_{2}(g)$
(iii) $N_{2}(g)+3H_{2}(g)\leftrightharpoons 2NH_{3}(g)$ the Equilibrium will remain unaffected on addition of Argon which is an inert gas.
Thus, the correct answer has to be the option (iv).
NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: MCQ (Type 2)
The Chapter 7 Equilibrium NCERT Exemplar MCQ questions are given below. The chapter is vast yet easy to learn. These solutions provide thorough explanations of the problems, helping students to apply theoretical concepts effectively.
Question 20. For the reaction $N_{2}O_{4}(g)\leftrightharpoons 2NO_{2}(g),$, the value of K is 50 at 400 K and 1700 at 500 K. Which of the following options is correct?
(i) The reaction is endothermic.
(ii) The reaction is exothermic.
(iii) If $NO_{2}$ (g) and $N_{2}O_{4}(g)$ are mixed at 400 K at partial pressures, 20 bar and 2 bar respectively, more $N_{2}O_{4}(g)$ will be formed.
(iv) The entropy of the system increases.
Answer:
The answer is the option (i), (iii) and (iv)
Explanation: K increases with the increase in temperature, and when K increases, the reaction must be endothermic. Thus, the number of molecules increases, and there is an increase in entropy.
Question 21. At a particular temperature and atmospheric pressure, the solid and liquid phases of a pure substance can exist in equilibrium. Which of the following term defines this temperature?
(i) Normal melting point
(ii) Equilibrium temperature
(iii) Boiling point
(iv) Freezing point
Answer:
The answer is the option (i) and (iv)
Explanation: Ice and water are in equilibrium only at a certain temperature and pressure. For any pure substance at atmospheric pressure, the temperature at which the solid and liquid phases are at equilibrium is called the normal melting point or normal freezing point of the substance.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: Short Answer Type
The Class 11 NCERT Exemplar Chemistry chapter 7 short answer type questions are given below. This chapter is vast yet easy to learn chapter.
Question 22. The ionisation of hydrochloric acid in water is given below:
$HCl(aq) + H_{2}O (l )\rightleftharpoons H_{3}O^{+} (aq) + Cl^{-} (aq)$
Label two conjugate acid-base pairs in this ionisation
Answer:
The two conjugate acid-base pairs in the reaction for the ionisation of Hydrochloric acid in water as per the given equation are
(1) $(HCl-Cl^{-})$ – Herein, $Cl^{-}$ is the conjugate base and HCl is the conjugate acid.
(2) $(H_{2}O-H_{3}O^{+})$ – Herein $H_{2}O$ is the conjugate base and $H_{3}O^{+}$ is the conjugate acid.
$HCl(aq)+H_{2}O\leftrightharpoons H_{3}O^{+}(aq)+Cl^{-}(aq)$
The conductance of any substance depends on the ions present in the solution since sodium chloride (NaCl) is an ionic compound which ionises completely in solution (NaCl has a dissociation rate of 100% i.e. it ionizes completely in water) forming an aqueous solution and hence the solution conducts electricity. Sodium Chloride ionizes into sodium ion (Na+) and chloride ion (Cl-) in water, which conducts electricity.
Hence, higher would be the number of ions of Socium Chloride in the water, higher would be the conductivity.
Question 24. $BF_{3}$ does not have proton but still acts as an acid and reacts with $NH_{3}$. Why is it so? What type of bond is formed between the two?
Answer:
$BF_{3}$ does not have a proton but still acts as an acid because it is an electron pair acceptor. This can be represented by
H3N : → BF3
Coordinate bond is formed between BF3 and NH3, and here Nitrogen acts as lone pair donator in this combination.
|
Base |
Dimethylamine |
Urea |
Pyridine |
Ammonia |
|
|
Arrange the bases in decreasing order of the extent of their ionization at equilibrium. Which of the above base is the strongest?
Answer:
As per the information available from the question, pKb values for Di-methylamine, ammonia, pyridine and urea are respectively 3.29, 4.752, 8.752, and 13.8861.
We know that, Higher is the value of Kb stronger will be the base. When we arrange then in decreasing order of extent of their ionization at equilibrium, they can be written as,
$5.4\times 10^{-4} > 1.77\times 10^{-5} > 1.77\times 10^{-9} > 1.3\times 10^{-14}$
So, the answer is Dimethylamine > Ammonia > Pyridine > Urea
Question 26. Conjugate acid of a weak base is always stronger. What will be the decreasing order of basic strength of the following conjugate bases?
$OH^{-}, RO^{-}, CH_{3}COO^{-} , Cl^{-}$
Answer:
$\begin{aligned} &\text {Conjugate acids of given bases are } \mathrm{H}_{2} \mathrm{O}, \mathrm{ROH}, \mathrm{CH}_{3} \mathrm{COOH}, \mathrm{HCl} \text { . }\\\\ &\text {Their acidic strength is in the order }\\ &\mathrm{HCl}>\mathrm{CH}_{3} \mathrm{COOH}>\mathrm{H}_{2} \mathrm{O}>\mathrm{ROH} \\ \\ &\text {Hence, basic strength is in the order : } \mathrm{RO}^{-}>\mathrm{OH}^{-}>\\ &\mathrm{CH}_{3} \mathrm{COO}^{-}>\mathrm{Cl}^{-} \end{aligned}$
Question 27. Arrange the following in increasing order of pH.
$KNO_{3}(aq), CH_{3}COONa(aq), NH_{4}Cl(aq), C_{6}H_{5}COONH_{4}(aq)$
Answer:
NH4Cl<C6H5COONH4<KNO3<CH3COONa
Salts of strong acid and strong base do not hydrolyse and form a neutral solution, thus, pH will be nearly 7 of KNO3. In sodium acetate, acetic acid remains unionised. This results in an increase in OH- concentration and pH will be more than 7. NH4Cl formed from a weak base, NH4OH and strong acid, HCl, in water dissociate completely, aq. ammonium ions undergo hydrolysis with water to form NH4OH and H+ ions resulting in less pH value.
Answer:
Now, as per the given information in the question
$2HI(g) \rightleftharpoons H_{2}(g) + I_{2}(g)$
It has also been specified that $K_{c} =1 \times 10^{-4}$
Now, when we apply the law of mass action the Equilibrium constant in this given equation we get;
$K_{c} =\frac{[H_{2}][I_{2}]}{[HI]^{2}}$
It is also known to us that the reaction quotient, $Q_{c}$, specifies the relative ratio of products to reactants at a given point in time.
$Q_{c} =\frac{[H_{2}][I_{2}]}{[HI]^{2}}$
$Q_{c} =\frac{(1\times10^{-5})(1\times10^{-5})}{(2\times10^{-4})}$
$Q_{c} =\frac{1}{4}=0.25$
Here, $Q_{c} >K_{c}$
Therefore, the reaction will proceed in reverse direction.
Question 29. On the basis of the equation pH = - log [H+ ], the pH of 10-8 mol dm-3 solution of HCl should be 8. However, it is observed to be less than 7.0. Explain the reason.
Answer:
As per the information given in the question, we can determine that the solution will be extremely dilute. It is also known to us that when HCl reacts with water it forms hydronium ion.
Thus, the large concentration of (H+) as a result, contributes to a decrease in the pH. Thus, here we cannot afford to ignore the concentration of H3O+ ions in the solution.
So, the total pH will be; $[H_{3}O^{+}] = 10^{-8} + 10^{-7} M \approx 7$
Therefore, the solution will be acidic.
Question 30. pH of a solution of a strong acid is 5.0. What will be the pH of the solution obtained after diluting the given solution 100 times?
Answer:
As per the information given in the question, we know that the pH=5.0
pH = 5 means [H+]=10−5 M,
On diluting it 100 times, we get
$[H^{+}]=\frac{10^{-5}}{100}=10^{-7}mol/L$
This should give pH = 7 but it cannot be so because solution is acidic and pH should be less than 7
The reason is that [H+] from H2O cannot be neglected. Thus, total [H+]=10−7M (from HCl) + 10−7M (from H2O ) =2×10−7M
∴pH=−log(2×10−7)= 7−0.3010=6.699
Answer:
As per the information given in the question, the solubility of $BaSO_{4}$ in water is $8 \times 10^{-4} g/L$
Hence, We can write the equation of disassociation of $BaSO_{4}$ as: -
$BaSO_{4}\rightleftharpoons Ba^{2+}++SO{_{4}}^{2-}$
|
At t=0 |
0 |
0 |
|
At t=0 |
S |
S |
Now, it is known to us that,
$K_{sp}=S\times S=S^{2}$
$K_{sp}=(8\times 10^{-8})^{2}$
$K_{sp}=64\times 10^{-8}$
Thus, in the presence of 0.01 $H_{2}SO_{4}$ soln
$H_{2}SO_{4}\rightleftharpoons 2H^{+}+SO{_{4}}^{2-}$
|
Initial |
0.01 |
0 |
0 |
|
Final |
0 |
0.02 |
0.01 |
Now we know that,
$BaSO_{4}\rightleftharpoons Ba^{2+}+SO{_{4}}^{2-}$
|
Final |
S |
S+0.01 |
The expression for Ksp in the presence of sulphuric acid will be
Ksp = (S) (S + 0.01)
Since value of Ksp will not change in the presence of sulphuric acid,
therefore,
(S) (S + 0.01) = 64 × 10–8
S2 + 0.01 S = 64 × 10–8
S2 + 0.01 S – 64 × 10–8 = 0
On solving quadratic equation, we get S= $6\times10^{-4}$.
Thus the solubility of $BaSO_{4}$ in 0.01 mol dm-3 of $H_{2}SO_{4}$ is $6\times10^{-4}$ mol dm-3
Question 32. pH of 0.08 mol dm-3$HOCl$ solution is 2.85. Calculate its ionisation constant.
Answer:
As per the information given in the question, C =0.08 mol dm-3 and pH =2.85
We know that the HOCl is a weak acid, therefore its dissociation will be written as-
$HOCl+H_{2}O\leftrightharpoons H_{3}O^{+}+OCl^{-}$
pH = -log [H+]
Thus, -2.85 = log [H+]
[H+] = antilog (-2.85)
[H+] = 1.41 × 10-3
We are aware that in case of a weak mono basic acid-
$H^{+}=\sqrt{K_{a}C}$
$[H^{+}]^{2}=K_{a}C$ (squaring both sides)
$K_{a}=\frac{[H^{+}]^{2}}{C}=\frac{(1.41\times 10^{-3})^{2}}{0.08}$
Thus, $K_{a}= 2.5\times 10^{-5}$
Therefore, we can conclude that the ionization constant of $HOCl$ will be $2.5\times 10^{-5}$
Question 33. Calculate the pH of a solution formed by mixing equal volumes of two solutions A and B of a strong acid having pH = 6 and pH = 4 respectively.
Answer:
pH of solution A = 6
Therefore, concentration of [H+ ] ion in solution A = 10-6 mol L-1
pH of solution B = 4
Therefore, concentration of [H+ ] ion in solution B = 10-4 mol L-1 .
On mixing one litre of each solution, total volume = 1L + 1L = 2L.
Amount of H+ ions in 1L of solution A= concentration x volume V= 10-6 mol X 1L
Amount of H+ ions in 1L of solution B= 10-4 mol X 1L
The total amount of H+ ions in the solution formed by mixing solutions A and B is (10-6 + 10-4 ) mol X 1L
This amount is present in 2L solution.
$Total\; [H^{+}]in\; 1L\; solution=\frac{10^{-6}+10^{-4}}{2}$
$=10^{-4}(1+\frac{0.01}{2})$
$=10^{-4}\times \frac{0.01}{2}$
$=5\times 10^{-5}mol/L$
Therefore, $pH=-log[H^{+}]=-log[5\times 10^{-5}]$
$=-log(5)+(-5\; log10)$
$=-log(5)+5=4.3$
Hence, the pH will be 4.3
Question 34. The solubility product of $Al(OH)_{3}$ is $2.7\times 10^{-11}$. Calculate its solubility in gL-1 and also find out the pH of this solution. (Atomic mass of $Al=27\; u$).
Answer:
As per the information given in the question,
$K_{sp} =2.7\times 10^{-11}$
Hence, we can write the equation of disassociation of $Al(OH)_{3}$ as -
$Al(OH)_{3}\rightleftharpoons Al^{3+}(aq)+3OH^{-}(aq)$
|
At t=0 |
1 |
0 |
0 |
|
At,t=t |
1-s |
s |
3s |
It is known to us that,
$K_{sp}= [Al^{3+}] [OH^{-}] ^{3-}$
$=(s)\times (3s)^{3}$
$=27s^{4}$
$S^{4}=\frac{K_{sp}}{27}$
$S^{4}=\frac{2.7\times 10^{-11}}{27}$
$S^{4}=10^{-12}$
$S=(10^{-12})^{\frac{1}{4}}=10^{-3}mol/L$
Now, molar mass of $Al(OH)_{3}=78$
Therefore, solubility = molar mass x s
$=78\times10^{-3}$
$=7.8\times10^{-2}g/L$
Now, it is known to us that,
pH = 14 - pOH
[OH]= 3s = 3 × 10-3
pOH= 3-log3
pH = 14 – 3 + log3
= 11.4771
Therefore, we can conclude that the solubility in g/L will be 7.8×10-2 g/L amd the pH of the solution will be 11.47.
Question 35. Calculate the volume of water required to dissolve 0.1 g lead (II) chloride to get a saturated solution. (Ksp of PbCl2 = 3.2 x 10-8, atomic mass of Pb = 207 u).
Answer:
As per the information available from the question, Ksp of PbCl2 = 3.2 ×10-8
Hence, we can write the equation of disassociation of PbCl2 as follows: -
$PbCl_{2}\rightleftharpoons Pb^{+2}(aq)+2Cl^{-}(aq)$
|
At t=0 |
1 |
0 |
0 |
|
At t=t |
1-x |
x |
2x |
$K_{sp}=[Pb^{2+}][Cl^{-}]^{2}$
On substituting the given values, we get
$=(x)\times (2x)^{2}=4x^{3}$
$4x^{3}=3.2\times 10^{-8}$
$x=2\times 10^{-3}mol/L$
We know that solubility is a product of molar mass $(PbCl_{2}) \times 2 \times 10^{-3}$
$=556\times 10^{-3}=0.556g/L$
0.1g of $PbCl_{2}$ will be dissolved in 0.1798 L (0.1/0.0556)
Thus, 0.1798 is the required volume to get a saturated solution of $PbCl_{2}$
As per the information given in the question,$NH_{3} + BF_{3}\rightarrow H_{3}N: BF_{3}$
$NH_{3} (N=1s^{2}2s^{2}2p^{1})$ is the Lewis acid in this reaction because it has a lone pair of e- to donate in its p-orbital. Moreover, the Lewis base in this case is BF3 as p-orbital of Boron is empty$(B=1s^{2}2s^{2}2p^{1})$. As such, it will be accepting lone pair from N to form a dative bond, as is clear from the lewis electronic theory. Thus, the Hybridisation of N is sp3 and B is sp2.
We know that,
$\Delta _{r}H^{\Theta } = \Delta _{f}H^{\Theta }[CO_{2}(g)]-\Delta_{f}H^{\Theta }[CaCO_{3}(s)]$
$\Delta _{r}H^{\Theta }= 178.3KJmol^{-1}$
.Thus As per the Le Chatelier’s Principle on increasing the temperature, the reaction will be shifting in the forward direction.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: Matching Type
NCERT Exemplar Class 11 Chemistry Chapter 7 Equilibrium important questions are discussed below. These are generally asked in exams to test your knowledge. These exemplar solutions is quite helpful for competitive exams.
Question 38. Match the following equilibria with the corresponding condition
|
Column I |
Column II | ||
|
(i) |
(a) |
Saturated solution | |
|
(ii) |
(b) |
Boiling point | |
|
(iii) |
(c) |
Sublimation point | |
|
(iv) |
(d) |
Melting point ‘ | |
|
|
|
(e) |
Unsaturated solution |
Answer:
(i)$\rightarrow$ (b); (ii)$\rightarrow$ (d); (iii)$\rightarrow$ (c); (iv) $\rightarrow$(a)
|
Column I (Reaction) |
Column II (Equilibrium constant) |
|
(i) $2N_{2}(g)+6H_{2}(g)\rightleftharpoons 4NH_{3}(g)$ |
(a) $2K_{c}$ |
|
(ii) $2NH_{3}(g)\rightleftharpoons N_{2}(g)+3H_{2}(g)$ |
(b) $K{_{c}}^{\frac{1}{2}}$ |
|
(iii) $\frac{1}{2}N_{2}(g)+\frac{3}{2}H_{2}(g)\rightleftharpoons NH_{3}(g)$ |
(c) $\frac{1}{K_{c}}$ |
|
|
(d) $K{_{c}}^{2}$ |
Answer:
(i)$\rightarrow$ (d); (ii)$\rightarrow$ (c); (iii) $\rightarrow$(b)
Question 40. Match standard free energy of the reaction with the corresponding equilibrium constant
|
(i)$\Delta G^{\ominus }>0$ | |
|
(ii)$\Delta G^{\ominus }<0$ | |
|
(iii) $\Delta G^{\ominus }=0$ | |
|
|
Answer:
(i)$\rightarrow$ (d); (ii) $\rightarrow$(a); (iii) $\rightarrow$(b)
Question 41. Match the following species with the corresponding conjugate acid.
|
Species |
Conjugate Acid |
|
(i) $NH_{3}$ |
(a)$CO{_{3}}^{2-}$ |
|
(ii)$HCO{_{3}}^{-}$ |
(b) $NH{_{4}}^{+}$ |
|
(iii) $H_{2}O$ |
(c) $H_{3}O^{+}$ |
|
(iv) $HSO{_{4}}^{-}$ |
(d) $H_{2}SO_{4}$ |
|
|
(e) $H_{2}CO_{3}$ |
Answer:
(i) $\rightarrow$ (b); (ii) $\rightarrow$ (e); (iii) $\rightarrow$ (c); (iv) $\rightarrow$ (d)
Question 42. Match the following graphical variation with their description
|
A |
B |
|
(i) |
(a) Variation in product concentration with time |
|
(ii) |
(b) Reaction at equilibrium |
|
|
(c) Variation in reactant concentration with time |
Answer:
(i) $\rightarrow$ (c); (ii) $\rightarrow$ (a); (iii) $\rightarrow$ (b)
Question 43. Match Column (I) with Column (II).
|
Column I |
Column II |
|
(i) Equilibrium |
(a) $\Delta G>0,K< 1$ |
|
(ii) Spontaneous reaction |
(b) $\Delta G=0$ |
|
(iii) Non-spontaneous reaction |
(c) $\Delta G^{\ominus }=0$ |
|
|
(d) $\Delta G<0,K> 1$ |
Answer:
(i) $\rightarrow$ c; (ii) $\rightarrow$ (d); (iii) $\rightarrow$ (a)
NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: Assertion and Reason Type
The Assertion and Reason type questions of Chapter 7 test students conceptual clarity and logical reasoning skills. These Equilibrium Class 11 NCERT Exemplar Solutions help you understand the basic concepts.
Question 44. In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): Increasing order of acidity of hydrogen halides is $HF < HCl < HBr < HI$
Reason (R): While comparing acids formed by the elements belonging to the same group of the periodic table, H-A bond strength is a more important factor in determining the acidity of acid than the polar nature of the bond.
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false.
(iv) Both A and R are false.
Answer:
The answer is the option (i) Both A and R are true, and R is the correct explanation of A
Explanation: H-A bond strength plays a more prominent role in determining the acidity than its polar nature. And as the size of A increases down the group corresponding to that the H-A bond strength decreases.
Question 45. In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): A solution containing a mixture of acetic acid and sodium acetate maintains a constant value of pH on addition of small amounts of acid or alkali.
Reason (R): A solution containing a mixture of acetic acid and sodium acetate acts as a buffer solution around pH 4.75.
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false.
(iii) Both A and R are false.
Answer:
The answer is the option (i) Both A and R are true, and R is the correct explanation of A.
Explanation: Buffer solutions are such solutions which resist a change in their pH on dilution or with the addition of small amounts of acid or alkali.
Question 46. In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): The ionisation of hydrogen sulphide in water is low in the presence of hydrochloric acid.
Reason (R): Hydrogen sulphide is a weak acid.
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false.
(iv) Both A and R are false.
Answer:
The answer is the option (ii) Both A and R are true, but R is not the correct explanation of A.
Explanation: There is a shift in the backward direction of the equilibrium.
Question 47. In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): For any chemical reaction at a particular temperature, the equilibrium constant is fixed and is a characteristic property.
Reason (R): Equilibrium constant is independent of temperature.
(i) Both A and R are true, and R is the correct explanation of A
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false
(iv) Both A and R are false.
Answer:
The answer is the option (iii) A is true, but R is false.
Explanation: The equilibrium constant for an exothermic reaction (negative H) decreases as the temperature increases. The equilibrium constant for an endothermic reaction (positive H) increases as the temperature increases.
Question 48. In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): Aqueous solution of ammonium carbonate is basic.
Reason (R): Acidic/basic nature of a salt solution of a salt of a weak acid and weak base depends on Ka and Kb value of the acid and the base forming it.
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false.
(iv) Both A and R are false.
Answer:
(i) Both A and R are true, and R is the correct explanation of A.
Explanation- Ka and Kb values are the ones responsible for acidic and basic characters of any compound.
Question 49. In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): An aqueous solution of ammonium acetate can act as a buffer.
Reason (R): Acetic acid is a weak acid, and $NH_{4}OH$ is a weak base.
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is false, but R is true.
(iv) Both A and R are false.
Answer:
The answer is the option (iii) A is false, but R is true.
Explanation: Salt of a weak acid and weak base can be used to form a buffer solution.
Question 50. In the following question, a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): In the dissociation of PCI5 at constant pressure and temperature addition of helium at equilibrium increases the dissociation of PCl5.
Reason (R): Helium removes Cl2 from the field of action.
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false.
(iv) Both A and R are false.
Answer:
(iv) Both A and R are false.
Explanation: If the volume remains constant and an inert gas such as argon is added, the equilibrium remains undisturbed because it does not take part in the reaction.
NCERT Exemplar Class 11 Chemistry Solutions Chapter 7: Long Answer Type
NCERT Exemplar Class 11 Chemistry Chapter 7 Equilibrium Long Answer Type questions test a students conceptual clarity and logical reasoning skills.
The values of $K_{c}$ (the equilibrium constant) and $Q_{c}$ (the reaction quotient) less than or greater than one another decides the direction in which reaction will proceed as follows-
(i) As $Q_{c} <K_{c}$, this implies that in order to reach the equilibrium, the concentration of the products must be increased, hence the reaction will proceed in the forward direction.
(ii) If $Q_{c} >K_{c}$, this implies that in order to reach the equilibrium, the concentration of the products must be decreased, hence the reaction will proceed in the backward direction.
(iii) If $Q_{c} =K_{c}$, no net reaction occurs as the equilibrium has been achieved.
As per the information given in the question, $N_{2}(g) + 3H_{2}(g) \rightleftharpoons 2NH_{3}(g) \;\Delta H = -92.38 \; kJ mol^{-1}$
Now, we know that as ΔH is negative, it means that the forward reaction is exothermic in nature.
As per the Le Chatelier principle, when the temperature is reduced the reaction will move in forward direction, hence more yield of the product will be obtained.
We know that when the temperature is increased the reaction will be moving in the backward direction that the yield of product will be reduced.
As per the Le Chatelier principle, when the pressure is increased the equilibrium shifts in the direction where there are lesser numbers of gas molecules. Therefore, when the pressure is increased, the equilibrium will be shifting in the forward direction and consequently the yield of the product will increase.
Thus, number of moles of reactants = 1 + 3 = 4
Number of moles of product = 2
Thus, we can conclude that high pressure and low temperature are the desirable conditions for increasing the yield of the products. Addition of an an inert gas at constant volume does not result in a shift. This is due to the fact that the addition of a non-reactive gas does not cause any change in the partial pressures of the other gases in the container.
In order to derive the relationship between the solubility and solubility product for such a salt we will take the following steps,
We will assume the solubility to be S.
Initially, we will assume that 1 mole of AxBy was present. Out of it, S moles were dissolved in order to give xS and yS moles of Ap+ and Bq- respectively. We can understand it better through the following equation: -
$A^{p+}\times B^{q-} y \leftrightharpoons xA^{+p} + yB^{-q}$
At t=0, 1 0 0
At Equilibrium, $1-S,xS \; Ys$
We know that, solubility product$(K_{sp}) = [A^{+p}]\times [B^{-q}]^{y}$
= $(xS)\times (yS)^{y}$
=$x^{x}Y^{y}S^{x+y}$
We can describe the relation between ΔG and Q as
ΔG = ΔG° + RT lnQ ...(1)
Herein, ΔG = Gibb’s energy change, ΔG° = standard Gibb’s energy, T = absolute temperature, Q = reaction quotient, and R = gas constant
We know that at Equilibrium, ΔG° = -RT lnK ...(2) (Wherein K is the Equilibrium constant)
Replacing the values of (2) in (1), we get
ΔG = -RT lnK + RT lnQ
ΔG = RT ln(Q/K) ...(3)
It is known to us that, Kc (which is the Equilibrium constant) is the ratio of concentration of products to that of reactants each raised to their stoichiometric coefficients at Equilibrium.
In contrast, Qc ( which is the reaction quotient) is the ratio of concentration of products to that of reactants each raise to their stoichiometric coefficients at any time during the reaction.
(a) In this case, if Q< K, it implies that the concentration of products has to be increased in order to reach Equilibrium concentration. Hence, the net reaction will proceed in the forward direction.
When Q= K, it implies that the Equilibrium has been achieved and no net reaction occurs. Now lets answer tehs econd part of the question.
(b) CO (g) + 3H2(g) $\rightleftharpoons$ CH4(g) + H2O (g) , As per the Le Chatiliers principle, when the pressure is increased, the Equilibrium will be shifting in that direction where there is a lesser number of gas molecules.
As per the available information,
Number of moles of reactants = 1 + 3 = 4
Number of moles of product = 1 + 1 = 2
Hence, the Equilibrium will shift in forward direction as number of moles of product is less. It is known to us that when Q < K, the Equilibrium will shift in the forward direction. Thus, for the given reaction Q < K
Class 11 Chemistry NCERT Chapter Equilibrium: Higher Order Thinking Skills (HOTS) Questions
HOTS questions of Chapter 7 NCERT Exemplar are designed to enhance analytical thinking and application-based understanding.
Question 1: Consider the following equilibrium,
$\mathrm{CO}(\mathrm{g})+2 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons \mathrm{CH}_3 \mathrm{OH}(\mathrm{g})$
0.1 mol of CO along with a catalyst is present in a $2 \mathrm{dm}^3$ flask maintained at 500 K Hydrogen is introduced into the flask until the pressure is 5 bar, and 0.04 mol of $\mathrm{CH}_3 \mathrm{OH}$ is formed. The $\mathrm{K}_{\mathrm{p}}^0$ is __________ $\times 10^{-3}$ (nearest integer).
Given : $\mathrm{R}=0.08 \mathrm{dm}^3$ bar $\mathrm{K}^{-1} \mathrm{~mol}^{-1}$
Assume only methanol is formed as the product and the system follows ideal gas behaviour.
Solution: $\mathrm{CO}(\mathrm{g})+2 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons \mathrm{CH}_3 \mathrm{OH}(\mathrm{g})$
$\begin{array}{llll}\mathrm{t}=0 & 0.1 \mathrm{~mol} & \mathrm{a} \text { mol } & - \\ \mathrm{t}_{\mathrm{eq}} & 0.1-\mathrm{x} & \mathrm{a}-2 \mathrm{x} & \mathrm{x}=0.04 \\ & =0.06 & =\mathrm{a}-0.08 & \\ & & =0.23-0.08 & \\ & & =0.15 \text { mole } & \end{array}$
$\begin{aligned} & \mathrm{V}=2 \mathrm{~L} \\ & \mathrm{~T}=500 \mathrm{~K} \\ & \mathrm{P}_{\text {total }}=5 \mathrm{bar} \\ & \mathrm{n}_{\text {Total }}=0.25=\frac{1}{4} \mathrm{~mol} . \\ & \mathrm{P}_{\text {total }}=\mathrm{n}_{\text {total }} \times \frac{\mathrm{RT}}{\mathrm{V}}\end{aligned}$
$\begin{aligned} & \Rightarrow 5=(0.06+\mathrm{a}-0.08+0.04) \times \frac{0.08 \times 500}{2} \\ & \Rightarrow 10=(0.02+\mathrm{a}) \times 0.08 \times 500\end{aligned}$
$\Rightarrow \mathrm{a}=0.25-0.02=0.23 \mathrm{~mol} .$
$\mathrm{K}_{\mathrm{P}}=\frac{\mathrm{X}_{\mathrm{CH}_3 \mathrm{OH}}}{\mathrm{X}_{\mathrm{CO}} \times \mathrm{X}_{\mathrm{H}_2}^2} \times \frac{1}{\left(\mathrm{P}_{\mathrm{T}}\right)^2}=\frac{0.04}{0.06 \times(0.15)^2} \times\left[\frac{1 / 4}{5}\right]^2$
$\begin{aligned} & =\frac{4}{6 \times(0.15)^2 \times 16} \times \frac{1}{25} \\ & =\frac{100 \times 100}{24 \times 225 \times 25}=\frac{100 \times 100}{135000} \\ & =0.074=74 \times 10^{-3}\end{aligned}$
Hence, the answer is 74.
Question 2: $37.8 \mathrm{~g} \mathrm{~N}_2 \mathrm{O}_5$ was taken in a 1 L reaction vessel and allowed to undergo the following reaction at 500 K
$$
2 \mathrm{~N}_2 \mathrm{O}_{5(\mathrm{~g})} \rightarrow 2 \mathrm{~N}_2 \mathrm{O}_{4(\mathrm{~g})}+\mathrm{O}_{2(\mathrm{~g})}
$$
The total pressure at equilibrium was found to be 18.65 bar.
Then, $\mathrm{Kp}=$ ______$\qquad$ $\times 10^{-2}$ [nearest integer]
Assume $\mathrm{N}_2 \mathrm{O}_5$ to behave ideally under these conditions
Given : $\mathrm{R}=0.082$ bar $\mathrm{L} \mathrm{mol}^{-1} \mathrm{~K}^{-1}$
Solution:
$
\begin{aligned}
& \text { Initial pressure of } \mathrm{N}_2 \mathrm{O}_5 \\
& =\frac{\frac{37.8}{108} \times 0.082 \times 500}{1}=14.35 \mathrm{bar} \\
& 2 \mathrm{~N}_2 \mathrm{O}_5 \rightleftharpoons 2 \mathrm{~N}_2 \mathrm{O}_4+\mathrm{O}_2 \\
& \mathrm{t}=0 \quad 14.35 \\
& \mathrm{t}=\mathrm{eq} \quad 14.35-2 \mathrm{P} \quad 2 \mathrm{P} \quad \mathrm{P} \\
& \mathrm{P}_{\text {Total }} \text { at } \mathrm{eqb}=14.35+\mathrm{P}=18.65 \\
& \mathrm{P}=4.3 \\
& \mathrm{P}_{\mathrm{N}_2 \mathrm{O}_{\mathrm{5}}}=5.75 \mathrm{bar} \\
& \mathrm{P}_{\mathrm{N}_2 \mathrm{O}_4}=8.6 \mathrm{bar} \\
& \mathrm{P}_{\mathrm{O}_2}=4.3 \mathrm{bar} \\
& \mathrm{k}_{\mathrm{p}}=\frac{(8.6)^2 \times(4.3)}{(5.75)^2}=9.619=\mathrm{x} \times 10^{-2} \\
& x=961.9 \approx 962
\end{aligned}
$
Hence, the answer is (962)
Question 3. In the following system, $\mathrm{PCl}_5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})$ at equilibrium, upon addition of xenon gas at constant $T \& p$, the concentration of
(1) $\mathrm{PCl}_5$ will increase
(2) $\mathrm{Cl}_2$ will decrease
(3) $\mathrm{PCl}_5, \mathrm{PCl}_3 \& \mathrm{Cl}_2$ remain constant
(4) $\mathrm{PCl}_3$ will increase
Solution:
Addition of xenon gas, an inert gas, to the equilibrium system $\mathrm{PCl}_5(\mathrm{~g}) \leftrightharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})$ at a constant temperature and pressure, it affects the equilibrium according to Le Chatelier's principle. The addition of an inert gas at constant pressure effectively increases the volume of the system, reducing the concentration of the gases involved.
Since the system is at constant pressure, adding an inert gas increases the total volume, which favors the side of the reaction with more moles of gas. In this reaction, there are two moles of gas on the right side $\left(\mathrm{PCl}_3\right.$ and $\left.\mathrm{Cl}_2\right)$ compared to one mole on the left $\left(\mathrm{PCl}_5\right)$. Thus, the equilibrium will shift toward the right to increase the number of moles and counteract the change, decreasing the concentration of $\mathrm{PCl}_5$ and increasing the concentrations of $\mathrm{PCl}_3$ and $\mathrm{Cl}_2$.
Hence, the correct answer is option (4).
Question 4: $\mathrm{~K}_{\text {sp }}$ of CdS is $8.0 \times 10^{-27}$ and that of $\mathrm{H}_2 \mathrm{~S}$ is $1 \times 10^{-22}$.
$1 \times 10^{-14} \mathrm{M} \mathrm{CdCl}_2$ solution is precipitated on passing $\mathrm{H}_2 \mathrm{~S}$ when pH is about $[\sqrt{1.25}=1.11]$
(1) 4
(2) 6
(5) 5
(4) 7
Answer:
$\begin{aligned} & \mathrm{H}_2 \mathrm{~S} \rightleftharpoons 2 \mathrm{H}^{+}+\mathrm{S}^{2-} \\ & C d S \rightleftharpoons C d^{2+}+\mathrm{S}^{2-} \\ & \mathrm{K}_{s p}(C d S)=\left[C d^{2+}\right]\left[\mathrm{S}^{2-}\right] \rightarrow 8 \times 10^{-27}=1 \times 10^{-14}\left[\mathrm{~S}^{2-}\right] \\ & \therefore\left[S^{2-}\right]=8 \times 10^{-13} \mathrm{M} \\ & \mathrm{K}_{\mathrm{H}_2 \mathrm{~S}}=\left[\mathrm{H}^{+}\right]^2\left[\mathrm{~S}^{2-}\right] \\ & \Rightarrow\left[\mathrm{H}^{+}\right]^2 \times 8 \times 10^{-13}=1 \times 10^{-22} \\ & \therefore\left[\mathrm{H}^{+}\right]^2=1.25 \times 10^{-10} \\ & {\left[\mathrm{H}^{+}\right]=1.11 \times 10^{-5} M} \\ & \therefore p H \approx 5\end{aligned}$
Hence, the correct answer is option (3).
Question 5: One litre buffer solution was prepared by adding 0.10 mol each of $\mathrm{NH}_3$ and $\mathrm{NH}_4 \mathrm{Cl}$ in deionised water.
The change in pH on addition of 0.05 mol of HCl to the above solution is_______$\times 10^{-2}$, (Nearest integer) (Given : $\mathrm{pK}_{\mathrm{b}}$ of $\mathrm{NH}_3=4.745$ and $\log _{10} 3=0.477$ )
Answer:
Initially
$\begin{aligned}
& \mathrm{pOH}=\mathrm{pK}_{\mathrm{b}}+\log \frac{\left[\mathrm{NH}_4 \mathrm{Cl}\right]}{\left[\mathrm{NH}_3\right]}=\mathrm{pK}_{\mathrm{b}}+\log \frac{0.1}{0.1} \\
& \mathrm{pOH}=\mathrm{pK}_{\mathrm{b}}
\end{aligned}$
$\mathrm{pH}=14-\mathrm{pOH} \Rightarrow \mathrm{pH}=9.255$
When 0.05 mol HCl is added
$\begin{array}{ccc}\mathrm{NH}_3 & +\mathrm{H}^{+} \rightleftharpoons & \mathrm{NH}_4^{+} \\ 0.1 & 0.05 & \\ 0.05 & 0 & 0.15\end{array}$
$\begin{aligned}
& \mathrm{pOH}=\mathrm{pK}_{\mathrm{b}}+\log \frac{0.15}{0.05}=5.222 \\
& \mathrm{pH}=8.778
\end{aligned}$
Change in $\mathrm{pH}=0.477$ or $47.7 \times 10^{-2}$
Hence, the answer is 0.477.
Question 6: A reversible gaseous reaction occurs in a closed vessel with movable piston: $\mathrm{A}(\mathrm{g}) \rightleftharpoons 2 \mathrm{~B}(\mathrm{~g})$ The concentration-time graph of $[\mathrm{A}]$ and $[\mathrm{B}]$ shows that the system reaches dynamic equilibrium. At $\mathrm{t}=8 \mathrm{~min}$, the volume of the container is suddenly doubled.
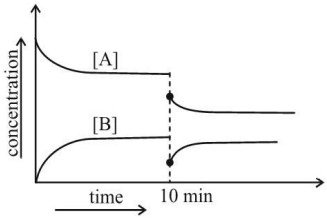
By observing the graph, predict the correct change at 10 Minutes time.
(1) Immediately after the volume increase, the equilibrium shifts towards A.
(2) Immediately after the volume increase, [A] slightly increases and the equilibrium shifts towards B.
(3) At the new equilibrium, the total moles of gas decrease.
(4) The reaction ceases to occur after the volume change
Answer:
Before $\mathrm{t}=8 \mathrm{~min}$ :
[A] decreases, [B] increases → system reaches dynamic equilibrium. At $t=10 \mathrm{~min}$ (volume doubled). Forward reaction produces more moles → equilibrium shifts towards B.
Concentration of $[\mathrm{A}]$ slightly increases immediately because reaction needs time to re-establish equilibrium.
New equilibrium: More B formed → total moles of gas increase, consistent with Le Chatelier's principle.
Hence, the correct answer is option (2).
Question 7: Given below are two statements
Statement I : A catalyst cannot alter the equilibrium constant (KC) of the reaction, temperature remaining constant
Statement II : A homogeneous catalyst can change the equilibrium composition of a system temperature remaining constant
In the light of the above statements, choose the correct answer from the options given below
(1) Statement I is false but Statement II is true
(2) Both Statement I and Statement II are true
(3) Both Statement I and Statement II is false
(4) Statement I is true but Statement II is false
Answer:
A catalyst speeds up both the forward and reverse reactions equally, allowing the system to reach equilibrium faster.
However, it does not change the energy difference between reactants and products (i.e., the Gibbs free energy change), which directly determines the equilibrium constant.
Thus, statement I is correct.
A homogeneous catalyst acts in the same phase as the reactants and, like any catalyst, it only helps the reaction reach equilibrium more quickly.
It does not alter the equilibrium position, meaning the relative concentrations of reactants and products at equilibrium remain unchanged if the temperature is constant.
Thus, statement II is false.
Hence, the correct answer is option (4).
Approach to Solve Questions of Chapter 7 Equilibrium
A clear understanding of the right approach is essential before solving questions from NCERT Class 11 Chemistry Chapter 7 Equilibrium. Given below are simple and effective methods that will help you solve each question accurately and with a structured approach
1. Before solving questions, of Chapter 7 it is important to have proper knowledge of basic concepts like dynamic nature, reversible reactions, equilibrium constant, Le Chatelier Principle, etc. Learning the concepts will help you attempt the Equilibrium questions with ease. Students can also refer to NCERT notes for Class 11 Chemistry Chapter 7 Equilibrium for conceptual clarity.
2. Equilibrium has a lot of numerical questions so try to memorize important formulas like Equilibrium Constant, Relationship Between $K_p$ and $K_c$, Reaction Quotient, pH and pOH, etc.
3. Questions related to graphs and trends are frequently asked in exams. Learn about Effect of temperature and pressure on equilibrium, Graphs of degree of dissociation vs concentration, pH variation of acids/bases, Solubility curves in ionic equilibrium.
4. It is important to learn to calculate pH and pOH using $-\log \left[H^{+}\right]$and using Ka or Kb values for weak acids/bases.
5. Students can start practising with theory-based questions to develop a clear understanding of the fundamental concepts of Equilibrium then proceed to numerical problems to strengthen their problem solving skills. Students can refer to NCERT Exemplar as it offers a variety of both conceptual and numerical questions.
Topics of NCERT Exemplar class 11 Chemistry Equilibrium
Topics covered in NCERT Chapter 6 Equilibrium is essential for learning the concepts of chemical and ionic balance.
- Equilibrium in physical processes
- Equilibrium in chemical processes
- Law of chemical equilibrium and equilibrium constant
- Homogeneous equilibrium
- Heterogeneous equilibrium
- Applications of equilibrium constants
- Relationship between equilibrium constant K reaction quotient and Q and Gibbs energy G
- Factors affecting equilibria
- Ionic equilibrium in solutions
- Acids, bases and salts
- Ionisation of acids and bases
- Buffer solutions
- Solubility equilibria of sparingly soluble salts
Important Formulas of Chapter 7 Equilibrium
Equilibrium has a lot of numerical questions so try to memorize important formulas like
1. Equilibrium Constant
$K_c=\frac{[C]^c[D]^d}{[A]^a[B]^b}$
2. Relationship Between $K_p$ and $K_c$
$K_p=K_c(R T)^{\Delta n}$
3. Reaction Quotient
$Q=\frac{[C]^c[D]^d}{[A]^a[B]^b}$
4. pH and pOH
$\mathrm{pH}=-\log \left[H^{+}\right]$
$\mathrm{pOH}=-\log \left[\mathrm{OH}^{-}\right]$
$\mathrm{pH}+\mathrm{pOH}=14$
5. Ostwald’s Dilution Law
$K=\frac{C \alpha^2}{1-\alpha}$
Advantages of Using Class 11 Chemistry Chapter 7 Equilibrium NCERT Exemplar Solutions
NCERT Exemplar Class 11 Chemistry Solutions Chapter 7 Equilibrium cover all concepts from the NCERT book in a simple and organised manner. The advantages of using these solutions of NCERT are given below:
- Students can understand concepts like dynamic equilibrium, equilibrium constant, Le Chateliers principle, chemical equilibrium, and ionic equilibrium using these solves questions.
- These NCERT Exemplar Class 11 Solutions help students to understand formulas and principles effectively.
- The class 11 chemistry chapter 7 equilibrium ncert exemplar solutions provides step by step explanations of equilibrium constant calculations and solubility product.
- By using these solutions students get clear explanations of topics that will help them prepare effectively for CBSE boards and competitive exams.
NCERT Exemplar Class 11 Chemistry Solutions Chapter-Wise
NCERT Exemplar problems are designed to strengthen conceptual understanding and analytical thinking. Students can follow the links given below to access all NCERT Exemplar Solutions for Class 11.
NCERT Solutions for Class 11 Chemistry Chapter-wise
Students can follow the links given below to access all NCERT Solutions for Class 11 Chemistry
NCERT Exemplar Class 11 Solutions
Students can follow the links given below to access NCERT Exemplar Solutions for other subjects for Class 11.
NCERT Solutions subject-wise
Given below are links for Class 11 NCERT Solutions
NCERT Notes subject-wise
Given below are links for Class 11 NCERT Notes
NCERT Books and NCERT Syllabus
Given below are links for Class 11 NCERT Books and Syllabus
Frequently Asked Questions (FAQs)
Equilibrium is a dynamic process. It's not that the reaction stops. Instead, the forward and reverse reactions continue to occur at equal rates. Reactants are still being converted to products, and products are still being converted back to reactants, but the overall concentrations stay constant because the rates are balanced.
Le Chatelier's Principle states that if a change of condition (a stress) is applied to a system in equilibrium, the system will shift in a direction that relieves the stress.
A catalyst does not affect the equilibrium position or the value of K. It only speeds up the rate at which equilibrium is reached. It lowers the activation energy for both the forward and reverse reactions equally.
K >> 1: The equilibrium lies far to the right, favoring the products. The reaction proceeds nearly to completion.
K << 1: The equilibrium lies far to the left, favoring the reactants. Very little product is formed.
K ≈ 1: Significant amounts of both reactants and products are present at equilibrium.
Change in concentration: Adding or removing reactants or products.
Change in Pressure: Caused by adding inert gas, changing the volume of the container.
Change in Temperature: Heating or cooling the system
A Statement & Reason question gives one factual statement and another supporting reason. You must decide whether both are true and whether the reason correctly explains the statement.
Chapter 7 covers important concepts such as the meaning of equilibrium, dynamic nature of equilibrium, law of mass action, equilibrium constant, factors affecting equilibrium , ionic equilibrium, pH, buffer solutions, solubility product, and common ion effect.
Students should begin by clearly understanding the dynamic nature of equilibrium and the laws that govern it. Practise numerical problems on equilibrium constants, pH, and solubility product, and regularly revise Le Chatelier’s principle to master how systems respond to changes in conditions.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters



