Previous year questions from Class 11 Physics Chapter 5 help students understand the exam pattern and important topics related to work, energy, and power. Practising these questions strengthens conceptual clarity, improves numerical problem-solving skills, and boosts confidence for examinations.
NCERT Class 11 Physics Chapter 6 Work, Energy and Power Notes - Download PDF
Have you ever been on a bicycle and tried to ride it up a hill, and how difficult it becomes, in comparison with riding a bicycle on a level road? That experience alone is a real-life example of ideas that you are going to study in NCERT Class 11 Physics Chapter 5 Notes Work, Energy and Power. This chapter will allow you to know how force causes motion, how to change one form of energy into another, and how power relates to the speed of doing work. It is one of the major chapters that learners want to achieve well in the CBSE board exams, JEE and NEET.
This Story also Contains
- NCERT Class 11 Physics Chapter 5 Notes: Download PDF
- Work, Energy and Power Class 11 Notes
- Class 11 Physics Chapter 5 Work, Energy and Power: Previous Year Questions
- How to Master Class 11 Physics Chapter 5 Work, Energy and Power?
- Importance of NCERT Class 11 Physics Chapter 5 Notes
- How to Use NCERT Class 11 Physics Chapter 5 Notes Effectively?
- NCERT Class 11 Notes Chapter-Wise
- Subject-Wise NCERT Exemplar Solutions
- Subject-Wise NCERT Solutions
- NCERT Books and Syllabus
The NCERT notes Class 11 Physics Chapter 5 Work, energy and power PDF offers properly organised descriptions of such important concepts as the work done by constant and variable forces, the kinetic energy, the potential energy, the conservation of mechanical energy, and the power. There are also step-by-step derivations, important formulae, examples, and simple diagrams in these NCERT notes Class 11 Physics Chapter 5 Work, energy and power to make learning easier. These NCERT notes help you prepare smartly, faster and more efficiently, whether you are reviṁsing before exams or developing a solid conceptual ground.
Also Read
NCERT Class 11 Physics Chapter 5 Notes: Download PDF
These Class 11 Physics Chapter 5 Work, energy and power Notes provide a clear and structured explanation of the concepts of work, energy, and power, along with important formulas, derivations, and solved examples. The downloadable PDF will help students with quick revision for CBSE exams as well as competitive exams like JEE and NEET.
Work, Energy and Power Class 11 Notes
The Class 11 Physics Chapter 5 Work, energy and power Notes provide easy-to-understand explanations and concise derivations, which help you prepare for exams. These Work, energy and power Class 11 Physics notes are helpful in gaining better knowledge and mastering the concepts covered in the chapter.
The Scalar Product
There are two ways of multiplying vectors (i) scalar product (ii) vector product. We shall study the latter in the next chapter. The scalar product or dot product of any two vectors $\vec{A}$ and $\vec{B}$, denoted as $\vec{A} \cdot \vec{B}$ (read as $\vec{A} \operatorname{dot} \vec{B}$ ) is defined as
$\vec{A} \cdot \vec{B}=AB\cos \theta$
where
Notions of Work and Kinetic Energy: The Work-Energy Theorem
This concept explains how work done on an object results in a change in its kinetic energy. When a force causes displacement, work is said to be done. The Work-Energy Theorem states that the net work done by all forces on an object is equal to the change in its kinetic energy.
$W_{\text {net }}=\Delta K E=\frac{1}{2} m v^2-\frac{1}{2} m u^2$
Work
If a force $\vec{F}$ is applied on a body in a direction different from the direction of displacement of the body, and the body undergoes a displacement $\vec{d}$ in the positive $X$-direction, as shown in Figure 2.
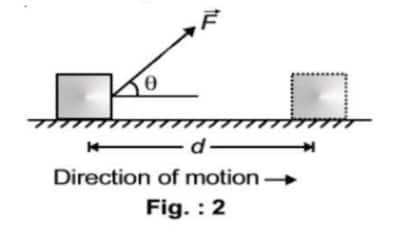
The work done by the force is defined as the product of the component of the force in the direction of the displacement and the magnitude of this displacement.
So, $W=(F \cos \theta) d=\vec{F} \cdot \vec{d}$
(i) Absolute units: Joule [S.I.] and Erg [C.G.S.]
(ii) Gravitational units: kg-m [S.I.] and gm-cm [C.G.S.]
Nature of work
- Positive work: $W=\vec{F} \cdot \vec{d}=F d \cos \theta$ So, work done is positive when $\theta$ is acute $\left(\theta<90^{\circ}\right)$, as $\cos \theta$ is positive.
- Negative work: $W=\vec{F} \cdot \vec{d}=F d \cos \theta$. Work done is negative when $\theta$ is obtuse $\left(\theta>90^{\circ}\right)$, as $\cos \theta$ is negative.
- Zero Work: $W=\vec{F} \cdot \vec{d}=F d \cos \theta=0$ when $F=0$ or $d=0$ or $\cos \theta=0\left(\theta=90^{\circ}\right)$
Work Done Calculation by Force Displacement Graph
The work done by a force on an object can be calculated using the area under the force-displacement graph.
$\begin{gathered}d W=F d x \\ \therefore W=\int_{x_i}^{x_f} d W=\int_{x_i}^{x_f} \vec{F} d x \\ \therefore W=\int_{x_i}^{x_f}(\text { strip area with width } d x) \\ \therefore W=\text { Area under curve Between } x_i \text { and } x_f\end{gathered}$
Energy
- The energy of a body is essentially its ability or capacity to get things done, or in other words, to do work.
- The SI unit of energy is the same as the work is Joule (J).
Kinetic Energy
Kinetic energy is the energy possessed by an object due to its motion.
Kinetic Energy $(\mathrm{KE})=\frac{1}{2} m v^2$
Where: KE is the kinetic energy, m is the mass of the object, and v is its velocity.
Work Done by a Variable Force
If the applied force (F) varies along the path, the work required to move a body from position A to B can be calculated by integrating the product of the force and differential displacement.
$
W=\int_A^B \vec{F} \cdot d \vec{s}=\int_A^B(F \cos \theta) d s
$
Relation of kinetic energy with linear momentum
$
\begin{gathered}
\mathrm{KE}(\mathrm{E})=\frac{1}{2} m v^2=\frac{1}{2}\left[\frac{p}{v}\right] v^2\{\text { from } \mathrm{p}=\mathrm{mv}\} \\
\Rightarrow \mathrm{E}=\frac{1}{2} p v \\
\mathrm{E}=\frac{p^2}{2 m}\{\text { fromv }=\mathrm{p} / \mathrm{m}\} \\
\text { And Momentum }(\mathrm{P})=\sqrt{2 m E}
\end{gathered}
$
The Work-Energy Theorem for a Variable Force
Confining to one dimension, the rate of change of kinetic energy with time is
$\begin{aligned} \frac{d K}{d t} & =\frac{d}{d t}\left(\frac{1}{2} m v^2\right) \\ & =\frac{1}{2} m \frac{d}{d t}\left(v^2\right) \quad(\text { since } m \text { is constant }) \\ & =\frac{1}{2} m\left(2 v \frac{d v}{d t}\right) \\ & =m \frac{d v}{d t} v \\ & =F v \quad\left(\text { as } F=m a=m \frac{d v}{d t} \text { from Newton's 2nd law }\right) \\ \therefore \quad \frac{d K}{d t} & =F \frac{d x}{d t} \\ d K & =F d x \\ \int_{K_i}^{K_f} d K & =\int_{x_i}^{x_f} F d x\end{aligned}$
[Integrating from the initial position (xi) to the final position (xf) ]
Where Ki and Kf are the initial and final kinetic energies corresponding to xi and xf, respectively.
or
Kf−Ki=∫Fdx
Thus, Kf−Ki=W
Thus, the work-energy theorem is proved for a variable force.
The Concept of Potential Energy
Potential energy is the energy that an object has because of its position or state.
Types of Potential Energy
Gravitational Potential Energy (GPE): It is the energy associated with an object's height in a gravitational field.
Potential energy = mgh
Where, U is the potential energy, m is the mass of the object, g is the acceleration due to gravity and h is the height of the object above a reference point.
Elastic Potential Energy: For objects like springs or rubber bands, the potential energy is associated with how much the material is stretched or compressed.
When an elastic spring is compressed (or strained) by a distance x from its equilibrium state, its elastic potential energy is represented by:
$U=\frac{1}{2} k x^2$
Where, k is the force constant of a given spring.
The Conservation of Mechanical Energy
The Law of Conservation of Energy asserts that energy is neither created nor destroyed; it merely changes from one form to another.
For simplicity, we are considerin g one-d imensional motion. Suppose that a body undergoes a displacement Δx under the action of a conservative force F . From the W-E theorem,
$\Delta K=F(x) \Delta x$
If the force is conservative, the potential energy function
$-\Delta U=F(x) \Delta x$
Adding the above two equations, we get
or
$
\begin{aligned}
& \Delta K+\Delta U=0 \\
& \Delta(K+U)=0
\end{aligned}
$
$\Rightarrow K+U$, the sum of the kinetic and potential energies of the body, is a constant.
Over the whole path $x_i$ to $x_f$
$
K_i+U_{x_i}=K_f+U_{x_i}
$
The quantity $K+U_x$ is the total mechanical energy of the system. Kinetic energy $K$ and the potential energy Ux may change individually from point to point, but the sum is a constant.
The Potential Energy of a Spring
When a spring is either compressed or stretched from its natural (equilibrium) position, it stores potential energy due to its elasticity. This energy is known as elastic potential energy.
According to Hooke's Law, the force required to stretch or compress a spring is
F=-kx
where:
The potential energy stored in the spring is given by the formula:
$U=\frac{1}{2} k x^2$
This energy increases with greater displacement and depends on the stiffness of the spring (value of k). The spring stores energy when deformed and releases it when it returns to its natural length.
Conservative and Non-Conservative Forces
The work done against which is stored in the system as its potential energy, which can be recovered later, is called a conservative force.
The work done against which is not stored in the system as its potential energy, which can be recovered later, is called a " non-conservative force".
Power
The power (P) of a body is defined as the rate at which the body can do work. Mathematically, power is expressed as the amount of work done (W) divided by the time (t) taken to do that work. The formula for power is:
$\begin{aligned} \text { Average Power }\left(P_{\text {avg }}\right)=\frac{\Delta w}{\Delta t}=\frac{\int_0^t p \cdot d t}{\int_0^t d t} \\ \text { Instantaneous } \operatorname{Power}(P)=\frac{d w}{d t}=P=\vec{F} \cdot \vec{v}\end{aligned}$
- Dimension of power: [ML2T-3]
- Unit of power: Watt or Joule/sec [S.I.], Erg/sec [C.G.S.]
- Practical unit: Kilowatt (kW), Megawatt (MW) and Horsepower (hp)
Collision
A collision occurs when two or more objects come into contact for a short period, during which they exert forces on each other. These forces can cause changes in the motion of the objects involved. Collisions are important because they help us understand how momentum and kinetic energy are transferred and conserved.
Types of collision
On the basis of conservation of kinetic energy, there are mainly three types of collisions
- Perfectly Elastic Collision: In a perfectly elastic collision, the system's kinetic energy is conserved, which means that the total kinetic energy before and after the collision is the same. There is no net loss or gain in kinetic energy, and the objects involved bounce off each other without deforming or losing energy to other forms.
- Inelastic collision: In an inelastic collision, the system's kinetic energy is not conserved; that is, the kinetic energy after the collision differs from the kinetic energy before the collision. Some of the initial kinetic energy is converted into different forms, such as internal energy, heat, or deformation.
- Perfectly inelastic collision: Inelastic collisions occur when the kinetic energy after the collision is less than the kinetic energy before the collision. In inelastic collisions, some of the initial kinetic energy is converted into other forms, while the total kinetic energy is not conserved.
Types of collision based on the direction of colliding bodies
Head-on or one-dimensional collision:
When the motion of colliding particles before and after the collision occurs along the same line, it is referred to as a "head-on" or "one-dimensional" collision. In such collisions, the initial and final velocities of the particles are aligned along a straight line, simplifying the analysis of the collision dynamics.
%20(1).jpeg)
$
\begin{aligned}
\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2 & =\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2 \\
m_1 u_1+m_2 u_2 & =m_1 v_1+m_2 v_2-(2)
\end{aligned}
$
$m_1, m_2$ : masses
$u_1, v_1$ : initial and final velocity of the mass
$m_1 u_2, v_2$ : initial and final velocity of the mass $m_2$
From equations (1) and (2), we get,
$
u_1-u_2=v_2-v_1 \ldots \ldots
$
From equations (1),(2), (3) We get
$
\begin{aligned}
& v_1=\left(\frac{m_1-m_2}{m_1+m_2}\right) u_1+\frac{2 m_2 u_2}{m_1+m_2} \\
& v_2=\left(\frac{m_2-m_1}{m_1+m_2}\right) u_2+\frac{2 m_1 u_1}{m_1+m_2}
\end{aligned}
$
Perfectly Elastic Oblique Collision:
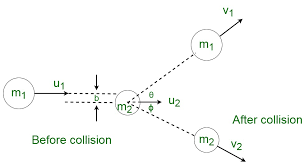
Let two bodies move as shown in the figure. By the law of conservation of momentum,
Along the x-axis-
$
m_1 u_1+m_2 u_2=m_1 v_1 \cos \theta+m_2 v_2 \cos \phi \ldots \text { - (1) }
$
Along $y$-axis-
$
0=m_1 v_1 \sin \theta-m_2 v_2 \sin \phi \ldots-(2)
$
By the law of conservation of kinetic energy
$
\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2 \ldots \text { - (3) }
$
So along the line of impact (here along in the direction of ) we apply $\mathrm{e}=1$
$
e=1=\frac{v_2-v_1 \cos (\theta+\phi)}{u_1 \cos \phi-u_2 \cos \phi} \ldots
$
So we solve these equations (1), (2), (3), (4) to get the unknown.
Perfectly Inelastic Collision
After a collision, two bodies stick together, resulting in a final common velocity.
When the colliding bodies are moving in the same direction
$
\begin{gathered}
m_1 u_1+m_2\left(-u_2\right)=\left(m_1+m_2\right) v \\
v=\frac{m_1 u_1-m_2 u_2}{m_1+m_2}
\end{gathered}
$
When the colliding bodies are moving in the opposite direction
$
\begin{gathered}
m_1 u_1+m_2 u_2=\left(m_1+m_2\right) v \\
v=\frac{m_1 u_1+m_2 u_2}{\left(m_1+m_2\right)}
\end{gathered}
$
Class 11 Physics Chapter 5 Work, Energy and Power: Previous Year Questions
Q1:
Two blocks $M_1$ and $M_2$ having equal mass are free to move on a horizontal frictionless surface. $M_2$ is attached to a massless spring as shown in the figure. Initially, $M_2$ is at rest, and $M_1$ is moving toward $\mathrm{M}_2$ with speed v and collides head-on with $M_2$.
Then choose the correct option
(a) While the spring is fully compressed, all the KE $M_1$ is stored as PE of the spring.
(b) While spring is fully compressed, the system momentum is not conserved, though final momentum is equal to initial momentum.
(c) If spring is massless, the final state of the $M_1$ is a state of rest.
(d) None of these
Answer:
a) The kinetic energy of $M_1$ is not fully transferred to the spring as its potential energy, and hence, option a is incorrect
b) The law of conservation of mass is valid here since the surface is frictionless; hence, option b is incorrect.
c) if we consider the case where the spring is totally massless, then all the kinetic energy $M_1$ gets transferred to $M_2$. As a result, m1 comes to rest, $M_2$ acquires a velocity v and starts moving. Hence, option c is correct.
Hence, the answer is option (c).
Q2:
A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.
(a) Work done by all forces on man is equal to the rise in potential energy, mgL.
(b) Work done by all forces on the man is zero.
(c) Work done by the gravitational force on the man is mgL.
(d) The reaction force from a step does not work because the point of application of the force does not move while the force exists.
Answer:
The gravitational force acts in a downward direction. The displacement is labelled L, which is in the upward direction. So, the work done on a man due to the gravitational force amounts to -mgL. Also, the work done to lift the man amounts to the force in the direction of displacement. Hence, the net force amounts to -mgL+ mgL = 0. Hence, statement (b) is correct.
The displacement at the point where the force acts is zero. Hence, the amount of work done by the force is also zero. So, statement (d) is correct.
Hence, the answers are options (b) and (d).
Q3:
A body of mass 0.5 kg travels in a straight line with velocity $v=a x^{\frac{3}{2}}$ where $a=5 \mathrm{~m}^{\frac{-1}{2}} \mathrm{~s}^{-1}$. The work done by the net force during its displacement from $x=0$ to $x=2 m$ is
(a) 1.5J
(b) 50J
(c) 10J
(d) 100J
Answer:
$
\begin{aligned}
& \mathrm{m}=0.5 \mathrm{~kg} \\
& v=a x^{\frac{3}{2}} \\
& a=5 m^{\frac{-1}{2}} s^{-1} \\
& \text { now, acceleration }=a=\frac{d v}{d t}=v \frac{d v}{d x} \\
& =a x^{\frac{3}{2}} \frac{d}{d x} a x^{\frac{3}{2}}=a x^{\frac{3}{2}} \times \frac{3}{2} \times a x^{\frac{1}{2}}=\frac{3}{2} a^2 x^2 \\
& \text { Net force }=m a=m\left(\frac{3}{2} a^2 x^2\right)
\end{aligned}
$
Work done under the variable force.
$
\begin{aligned}
& =\int_{x=0}^{x=2} F . d x=\int_0^2 \frac{3}{2} m a^2 x^2 d x \\
& =\frac{1}{2} m a^2 \times 8=\frac{1}{2} \times(0.5) \times(25) \times 8=50 J
\end{aligned}
$
Hence, the answer is the option (b).
Q4:
A carriage of mass $M$ and length $\ell$ is joined to the end of a slope as shown in the figure. A block of mass $m$ is released from the slope at height $h$. It slides till the end of the carriage. The friction between the mass and the slope, and also the friction between the carriage and the horizontal floor, is negligible. Coefficient of friction between block and carriage is $\mu$. Find $h$ in terms of the given parameters.
Answer:
Suppose the velocity of the block at the end of slop $=v$
Then, by the work-energy theorem
$
m g h=\frac{1}{2} m v^2
$
Now,
Since there is no external force on the (cart + block) system
$
\begin{aligned}
& P_i=P_f \\
& m v=(m+M) v^{\prime} \\
& v^{\prime}=\frac{m v}{m+m}
\end{aligned}
$
Now, work done by friction $=$ change in kinetic energy of the system.
$
\begin{aligned}
& -\mu m g \ell=\frac{1}{2}(m+M) v^{\prime 2}-\frac{1}{2} m v^2 \\
& \mu m g \ell=\frac{1}{2} m v^2-\frac{1}{2}(m+M) \frac{m^2 v^2}{(m+M)^2} \\
& h=\mu\left(\frac{m+M}{M}\right) \ell
\end{aligned}
$
Q5:
Consider two blocks A and B of masses $m_1=10$ kg and $\mathrm{m}_2=5 \mathrm{~kg}$ that are placed on a frictionless table. The block A moves with a constant speed $v=3 \mathrm{~m} / \mathrm{s}$ towards the block B kept at rest. A spring with spring constant $\mathrm{k}=3000 \mathrm{~N} / \mathrm{m}$ is attached to the block B as shown in the figure. After the collision, suppose that the blocks A and B, along with the spring in a constant compression state, move together, then the compression in the spring is (Neglect the mass of the spring)
Answer:
Here, once the two Blocks are moving together, we can replace this two-body problem with a one-body problem with reduced mass $m=\frac{m_1 m_2}{m_1+m_2}$.
From conservation of energy
$\frac{1}{2} m v_{r e}^2=\frac{1}{2} k x^2$.
$
\begin{aligned}
&\ x=\sqrt{\frac{m_1 m_2}{\left(m_1+m_2\right) k}} \text {. } \text { Vrel }\\
&\begin{aligned}
& =\sqrt{\frac{10 \times 5}{15 \times 3000}} \times 3 \\
& =\frac{1}{30} \times 3=\frac{1}{10} \mathrm{~m}=0.1 \mathrm{~m}
\end{aligned}
\end{aligned}
$
How to Master Class 11 Physics Chapter 5 Work, Energy and Power?
The fifth chapter of Class 11 Physics is simplified when one realises the relationship between work, energy, and power in things occurring around us. Conceptual and numerical practice, particularly the work-energy theorem, calculations of kinetic energy, potential energy, and power, are involved in this chapter. Learning is useful in passing exams with good scores and provides a foundation for the other detailed subjects in upper grades.
- Before you can learn when work is positive, negative, or zero, you need to understand the meaning of work by force and which situations are considered to be positive, negative, or zero, using simple examples such as pushing a trolley or lifting a book.
- Learn the Work-Energy Theorem and solve numerical problems that are based on change in kinetic energy-they are on many exams.
- Know how to distinguish between kinetic and potential energy and know the way of how energy can be stored and transformed in systems such as springs, falling bodies, and moving objects.
- Revise the derivation of kinetic energy, potential energy (mgh), and the elastic potential energy and exercise by using them in various circumstances.
- Learn conservative and non-conservative forces using such examples as the gravitational force (conservative) and friction (non-conservative).
- Memorise formulae of average and instantaneous power and practice examples of them in life, like doing work slowly or fast.
- Solve numerical problems dealing with graphs of forces and displacement because many of the questions in the exams deal with the area under the curve.
- Learn to identify the system correctly in each question and choose whether to apply the work-energy theorem or direct formulas.
- Keep the significant formulas up to date and come up with a small formula sheet that you can use to revise on a regular basis and before exams.
- Solve NCERT exercise questions, exemplar problems, and previous year questions to strengthen speed and accuracy.
Importance of NCERT Class 11 Physics Chapter 5 Notes
NCERT notes Class 11 Physics Chapter 5 Work, energy and power are essential for understanding how work, energy, and power operate in physical processes. These Work, energy and power Class 11 Physics notes simplify complex concepts, highlight important formulas, and help students revise quickly for exams. They also strengthen the foundation needed for competitive exams like JEE and NEET.
Good Conceptual Understanding
- The Work, Energy and Power Class 11 Notes break down complicated learning points, such as the work done by a force, kinetic energy, potential energy, and power and enable students to find good basics to be used during exams
Exam-Oriented Preparation
- A good revision of the major formulas, derivations, numbers, etc. that are recurrently tested in CBSE Class 11 exams, JEE and NEET is facilitated by exam-related notes.
Quick Revision Material
- NCERT Class 11 Physics Chapter 5 Notes PDF comes in handy during last-minute revision and is the best guide with all the important definitions, laws, and problem-solving methods in a succinct form.
Increases Competitive Examination Preparation
- Physics concepts such as the work-energy theorem, conservation of energy, and collision are vital in JEE Mains, JEE Advanced, and NEET Physics, and these notes reduce the difficulty in solving problems.
Well-Structured and Time-Saving
- The notes are planned according to the chapters in a step-by-step manner, thus enabling students to save time and maintain focus when doing revisions.
Bridges Theory and Application
- The notes include the solved examples and shortcuts, and help students to comprehend how to use the Physics concepts in reality and the numerical problems.
How to Use NCERT Class 11 Physics Chapter 5 Notes Effectively?
The NCERT Class 11 Physics Chapter 5 study notes come in very handy in enlightening one about the fundamental concepts of work, energy and power without being lost in the terminology. These notes can make learning less difficult, save time on revision and help to do better on exams when used appropriately.
- To have a simple idea of the chapter, begin with the notes. This will make you know what the chapter is all about, before it starts explaining things in detail.
- Try to learn concepts such as work, kinetic energy, potential energy, and power using simple examples as opposed to simple memorisation of formulae.
- Make a little list of formulas, which are in the notes and revise it regularly so that one does not forget them during examinations.
- Once reading the notes is done, work with numerical problems to observe how every formula is practically applied.
- The notes contain diagrams and solved examples, which help to understand concepts more accurately and remember them better, so pay attention to them.
- Read the notes regularly, particularly during exams, to put ideas in your mind.
- In case of any confusion with a point in the notes, you should consult your textbook or teacher rather than skipping it.
NCERT Class 11 Notes Chapter-Wise
Get well-structured and easy-to-understand NCERT Class 11 Physics Notes Chapter-Wise to strengthen your exam preparation. These notes cover all important concepts, formulas, and derivations as per the latest CBSE syllabus, making them helpful for board exams and competitive exams like JEE & NEET
Subject-Wise NCERT Exemplar Solutions
NCERT Exemplar Solutions for Class 11 provide additional practice through higher-order and application-based questions. The subject-wise links help students strengthen conceptual clarity and improve problem-solving skills for exams and competitive tests.
Subject-Wise NCERT Solutions
NCERT Solutions for Class 11 offer detailed, step-by-step answers to all textbook questions across subjects. These subject-wise links make learning organised and help students prepare effectively for school exams.
NCERT Books and Syllabus
NCERT Books and the NCERT Syllabus for Class 11 form the backbone of the academic curriculum. Easy access to these links helps students understand the prescribed course structure and study systematically as per the latest guidelines.
Frequently Asked Questions (FAQs)
Q: What is the difference between work and energy?
A:
Work is the transfer of energy when a force is applied to an object, causing displacement. Energy, on the other hand, is the capacity to do work. The unit of work and energy is the joule (J).
Q: What is the work-energy theorem?
A:
The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy.
Q: What is the significance of the Work, Energy, and Power chapter in Physics?
A:
This chapter introduces fundamental concepts that form the basis for understanding various physical phenomena. It helps explain how energy is transferred, how work is done, and how power is calculated in mechanical systems, making it essential for both academic exams and real-life applications.
Q: Why is power important in this chapter?
A:
Power helps quantify how quickly work is done or energy is transferred. Understanding power is crucial in practical scenarios, such as determining the efficiency of machines and engines or calculating the speed at which energy is consumed.
Q: How does this chapter help in competitive exams like JEE or NEET?
A:
The concepts of work, energy, and power are foundational for various topics in competitive exams, especially mechanics and thermodynamics. Understanding these helps in solving a wide range of problems, improving both speed and accuracy in exams.
Q: Why is understanding the work-energy theorem crucial for revision?
A:
According to the work-energy theorem, an object's change in kinetic energy equals the work that the net force has done on it. This concept makes problem-solving easier and helps in connecting various mechanics topics during revision by enabling students to directly relate force, motion, and energy transformations in physical systems.
Q: For mastering the concepts of Work, Energy, and Power, what is the ideal sequence for revisions?
A:
Students should revise in the following order for systematic learning:
- Work and its calculation.
- Concepts of kinetic and potential energy
- Both conservative and non-conservative forces
- The work-energy theorem
- The mechanical energy conservation law
- Power and its calculations and units
This sequence gradually connects concepts and develops fundamental understanding.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters