Kinetic Theory Class 11th Notes - Free NCERT Class 11 Physics Chapter 13 Notes - Download PDF

NCERT Notes for Class 11 Physics Chapter 12: Download PDF

NCERT Notes Class 11 Physics Chapter 12: Kinetic Theory of Gases prepared by subject experts as per the latest CBSE syllabus. These notes give you a brief explanation, important formulas, and significant derivations so that you can revise fast and efficiently. The students can get the PDF and reinforce their knowledge of the ideas and succeed in the CBSE examinations, JEE, and NEET.

Download PDF

NCERT Notes for Class 11 Physics Chapter 12

The NCERT Notes of Class 11 Physics Chapter 12 - Kinetic Theory of Gases provide an easy and systematic explanation of such important concepts as the molecular motion, pressure, temperature, and gas laws. The notes will assist students in understanding the microscopic behaviour of gases without complications. They are highly beneficial to applicants of CBSE, JEE, and NEET as well as those who need to revise fast and prepare exams within a short time frame.

Properties of Gases

Some properties of gases

• Gases can be compressed easily.

• Gases have neither a definite volume nor a definite shape.

• When a substance is in the gaseous state, its density is very small in comparison to the density in its solid or liquid state.

Boyle’s Law

• At constant temperature, the volume V of a given mass of a gas is inversely proportional to its pressure P, according to Boyle's law

$\begin{aligned} & V \propto \frac{1}{P} \\ & P V=\text { constant }\end{aligned}$

• If P₁ and V₁ are the initial pressure and volume, and P₂ and V₂ are the final pressure and volume for a given mass of a gas at constant temperature, then

$P_1 V_1=P_2 V_2$

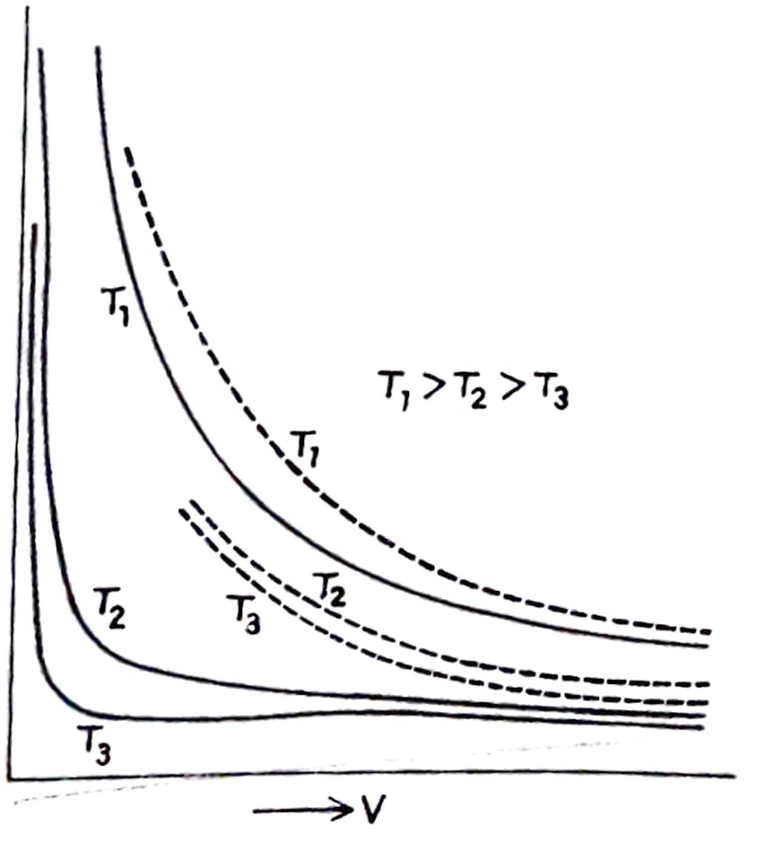
• A graph is drawn between P and V for a gas at different constant temperatures T₁, T₂, and T₃ (T₁> T₂>T₃).
• The gases do not obey Boyle’s law strictly under all conditions of pressure and temperature; gases only obey Boyle’s law at low pressures and high temperatures.

Charles’ Law

• At constant pressure, the volume of the given mass of a gas increases by $\frac{1}{273} t h$ part of its volume at 0℃ for a 1℃ rise in temperature is called Charles's law.

$V_t=V_0\left(1+\frac{t}{273}\right)$

• Charles’ Law in terms of absolute temperature:- Let at constant pressure, the volume of a given mass of a gas at 0℃, t₁℃ and t₂℃ are V₀, V₁ and V₂ respectively. T₁ and T₂ are the absolute temperatures corresponding to t₁℃ and t₂ ℃. By Charles' Law

$\begin{aligned} & V_1=V_0\left(1+\frac{t_1}{273}\right)=V_0\left(\frac{273+t_1}{273}\right) \\ & V_2=V_0\left(1+\frac{t_2}{273}\right)=V_0\left(\frac{273+t_2}{273}\right) \\ & \therefore \frac{V_1}{V_2}=\frac{273+t_1}{273+t_2}=\frac{T_1}{T_2} \\ & \frac{V_1}{T_1}=\frac{V_2}{T_2} \\ & \frac{V}{T}= \text { constant } \tan t \\ & V \propto T\end{aligned}$

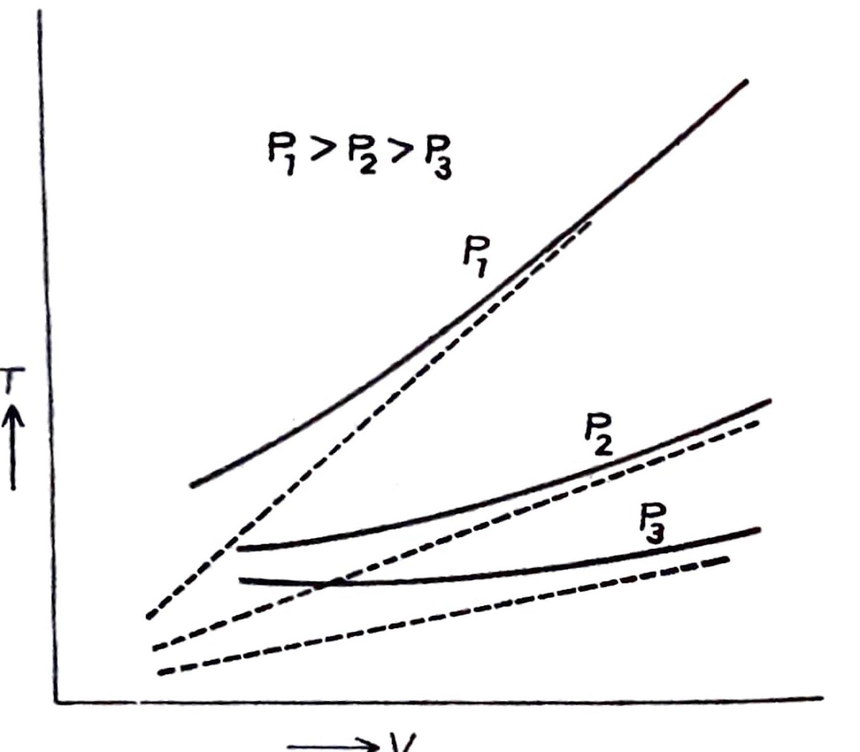
Therefore, at constant pressure, the volume of a given mass of a gas is directly proportional to its absolute temperature. This is Charles’ Law in terms of absolute temperature.

• A graph is drawn between T and V for a gas at three different constant pressures P₁, P₂, and P₃ ( P₁> P₂>P₃).

Perfect Gas ( or ideal gas)

• A gas whose properties are similar to the properties of a real gas at infinitely low pressure, such an imaginary gas, is called a perfect gas or an ideal gas.
• The following are the properties of a perfect gas:

1. It strictly obeys Boyle's Law, Charles’ Law and the law of pressure under all conditions of temperature and pressure.

2. Its pressure coefficient and volume coefficient are exactly equal to each other.

3. Its molecules are infinitesimally small.

4. There is no force of attraction between its molecules.

Equation of State for an Ideal Gas

• Let initially pressure, volume, and temperature of a gas are P₁, V₁, and T₁, respectively and finally change to P₂, V₂, and T₂, respectively. Now,

i. Let the temperature of the gas be kept constant at T₁, and the pressure is changed from P₁ to P₂. If in this process the volume changes from V₁ to V₂ then by Boyle’s law,

$
\begin{aligned}
& P_2 V_2=P_1 V_1 \\
& V_2=\frac{P_1 V_1}{P_2}
\end{aligned}
$

ii. Let the pressure of the gas be kept constant at P₂, and its absolute temperature is changed from T₁ to T₂. If in this process the volume of the gas changes from V₁ to V,₂ then by Charles’ law,

$
\begin{aligned}
& \frac{V_1}{T_1}=\frac{V_2}{T_2} \\
& V_2=\frac{T_1 V_1}{T_2}
\end{aligned}
$

From equations (i) and (ii), we have

$\begin{aligned} & \frac{P_1 V_1}{P_2}=\frac{T_1 V_2}{T_2} \\ & \frac{P_1 V_1}{T_1}=\frac{P_2 V_2}{T_2}\end{aligned}$

Hence, for a gas, the volume of PV/T remains constant. Let this constant be equal to K, then

$\begin{aligned} & \frac{P V}{T}=K \\ & P V=K T\end{aligned}$

We can write K = nk, where k is the same for all gases. It is called the Boltzmann constant.

$P V=n k T \quad \ldots \ldots(i i i)$

If P, V, and T are the same, then n is also the same for all gases.

If we take 1 gram-molecule (1 mole) of a gas-constant it will be the same for all gases. Then it is called the universal gas constant, and it is represented by R. Then,

$P V=R T$

Where R = Nk, where N = Avogadro’s number and k = Boltzmann constant

It is called the ideal gas equation or perfect gas equation.

• The gas equation for μ moles of gas will be

$P V=\mu R T \quad \ldots \ldots(i v)$

• Unit of R:- Unit of R is Jmol⁻¹K⁻¹
• Dimension of R:- [ML²T⁻²K⁻¹].
• Numerical value of R:- The value of R is 8.31Jmol⁻¹K⁻¹.

Kinetic Theory of Gases

The following are the fundamental assumptions of the kinetic theory of gases:

• A gas is composed of a large number of tiny, invisible, perfectly elastic particles, called molecules.
• The molecules are always in a state of continuous motion with varying velocities in all possible directions.
• The molecules traverse the straight path between any two collisions.
• The size of the molecules is infinitely small compared to the average distance traversed by a molecule between any two consecutive collisions. The distance between any two consecutive collisions is called the free path, and the average distance between any two consecutive collisions is called the mean free path.
• The time of collisions is negligible compared with the time taken to traverse the free path.
• The collisions between molecules and with the walls are perfectly elastic, so that there is no loss of kinetic energy in the collisions.
• The molecules exert no force on each other except when they collide, and the whole of the molecules' energy is kinetic.
• The volume of the molecules is negligible compared to the volume of a vessel containing gas.
• The intermolecular distances in a gas are much larger than that of a solid or liquid, and the molecules of a gas are free to move in the entire space available to them.

Pressure Exerted by an Ideal Gas

• When a certain mass of a perfect gas is confined in a vessel, the molecule frequently collides with the walls of the vessel and are reflected from the walls. During the collision with the walls, each molecule suffers a change in momentum.

• According to Newton‘s second law of motion, the rate of momentum is equal to the force exerted. Thus, it exerts pressure on the walls. This pressure may be calculated on the basis of postulates of the kinetic theory of gases.

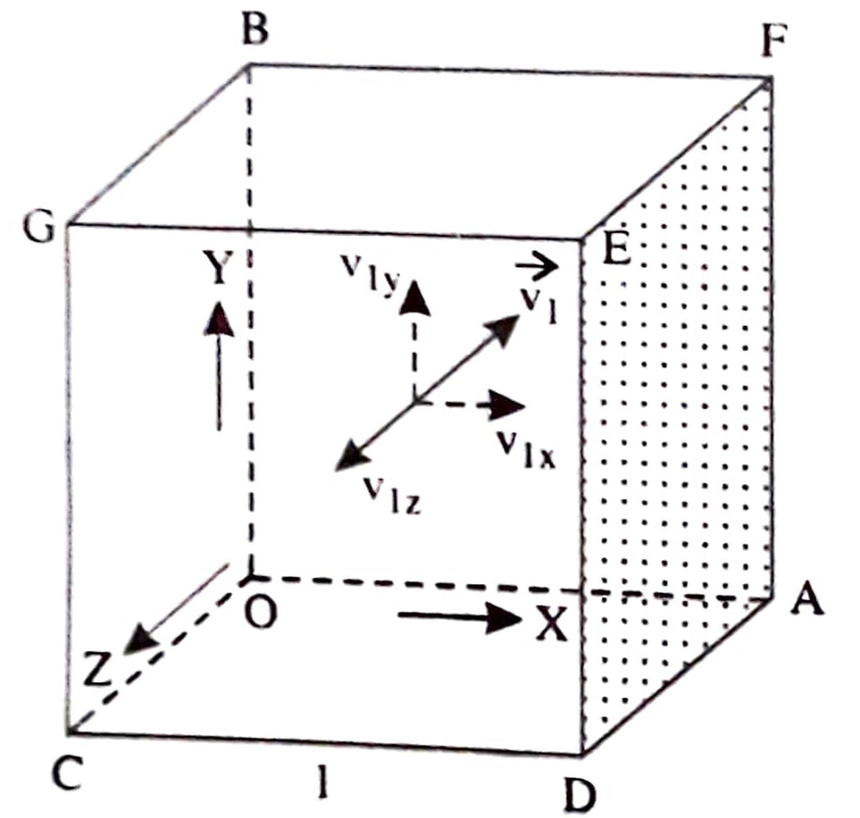
Let us consider a perfect gas contained in a cubical vessel of side (l) and perfectly elastic walls. Let n be the total number of molecules of a gas in the vessel, and m be the mass of a molecule. Let the sides of the cube represent mutually perpendicular X, Y, and Z-axes.

Consider a molecule P moving in a random direction with velocity v₁. Let v_1x, v_1y, and v_1z be the components of the velocity v₁ along three mutually perpendicular X, Y, and Z axes, respectively.

Then

$v_1^2=v_{1 x}^2+v_{1 y}^2+v_{1 z}^2$

The component of velocity with which the molecule P will strike the face DEFA is v_1x, and the momentum of the molecule in X-direction before collisions

$=m v_{1 x}$

As the molecule and the wall are perfectly elastic, during collision speed of the molecule does not change, and only the direction of velocity is changed.

Therefore, the momentum along X- axis after collisions

$=m\left(-v_{1 x}\right)=-m v_{1 x}$

The change in momentum during one collision along X-axis

$=m v_{1 x}-\left(-m v_{1 x}\right)=2 m v_{1 x}$

The molecule suffering reflection at face DEFA traverses a distance l and strikes the face CGBO. It is equal to the force exerted on it. Hence, the force exerted by the molecule on the wall A will be mv_x²/l. Since there are n molecules, the total force exerted on the wall A is given by

$\frac{m}{l}\left(v_{x_1}^2+v_{x_2}^2+\ldots \ldots v_{x_n}^2\right)$

Where v_xn is the x-component of the velocity of molecule 1, v_x2 of molecule 2,.... And so on. Since the area of the wall is l², the pressure on the wall A is given by

$\begin{aligned} & P=\frac{m}{l^3}\left(v_{x_1}^2+v_{x_2}^2+\ldots \ldots v_{x_n}^2\right) \\ & =\frac{m n}{l^3}\left(\frac{\left(v_{x_1}^2+v_{x_2}^2+\ldots \ldots v_{x_n}^2\right)}{n}\right) \\ & \text { But } l^3=\vee \\ & \therefore P=\frac{m n}{V}\left(\frac{\left(v_{x_1}^2+v_{x_2}^2+\ldots \ldots v_{x_n}^2\right)}{n}\right)\end{aligned}$

Now, $\left(\frac{\left(v_{x_1}^2+v_{x_2}^2+\ldots \ldots v_{x_n}^2\right)}{n}\right)$ is the average value of v_x² for all the n molecules. This can be written as

$\overline{v_x^2}$

Therefore,

$P=\frac{m n}{V} \bar{v}_x^2 \quad \ldots \ldots(i)$

We know that for any molecule, we have

$
v^2=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2} \quad \ldots \ldots
$

Because this equation is true for every molecule, this will also be true for the mean value of all the molecules.

$\therefore v^{\overline{2}}=\bar{v}_x^2+\bar{v}_y^2+\bar{v}_z^2 \quad \ldots \ldots(i i i)$

The directions of the molecules are quite at random; that is, all directions are equally possible. Hence, the values, of $\overline{v_x^2}, \overline{v_y^2}, \overline{v_z^2}$ will be equal, ie. $\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}$

Therefore, from eqn (ii), we have

$
\begin{aligned}
\overline{v^2} & =3 \overline{v_x^2} \\
\overline{v_x^2} & =\frac{1}{3} \overline{v^2}
\end{aligned}
$

or

$
P=\frac{1}{3} \frac{m n}{V} \overline{v^2} \ldots \ldots(i i i)
$

This is the equation for the pressure of the gas. $\overline{v^2}$

is called the mean-square velocity of the molecules. Since mn is the mass of the whole gas and V is the volume, so mn/V is the density ⍴ of the gas. Therefore, the above expression can be written as

$P=\frac{1}{3} \rho \bar{v}^2 \quad \ldots .(i v)$

Again,

$P=\frac{1}{3} \rho v^2=\frac{2}{3}\left(\frac{1}{2} \rho \overline{v^2}\right)=\frac{2}{3} E$

Where $E=\left(\frac{1}{2} \rho \overline{v^2}\right)$ is the transnational kinetic energy of the gas per unit volume. Thus, the pressure is equal to two-thirds of its transnational kinetic energy per unit volume.

Root mean-Square (rms) Speed of a gas molecule

• The speeds of the individual molecules of a gas vary over a wide range. Let v₁, v₂, and v₃…...vₙ. Be the speed of molecules of a gas. Then, the root-mean-square speed of the molecules is defined as the square root of the mean of the squares of the speeds of all gas molecules, and it is denoted by rms. Thus,

$v_{r m s}=\sqrt{\overline{v^2}} \sqrt{\frac{v_1^2+v_2^2+v_3^2}{n}}$

• We know that the pressure of a gas is given by

$\begin{aligned} & P=\frac{1}{3} \rho \overline{v^2} \\ & v_{r m s}=\sqrt{\overline{v^2}}=\sqrt{\frac{3 P}{\rho}}\end{aligned}$

Interpretation of temperature on the basis of the Kinetic theory

Let us consider 1 gram molecule of a gas at absolute temperature, T, occupying a volume V. According to the Kinetic theory, the pressure of the gas

$\begin{aligned} & P=\frac{1}{3} \cdot \frac{m N}{V} \overline{v^2} \ldots \ldots(i) \\ & P V=\frac{1}{3} m N \overline{v^2} \because \ldots(i i) \\ & \because P V=R T \ldots \ldots(i i i) \end{aligned} $

And mN = M

Comparing eqn (ii) and (iii)

$\begin{aligned} & \frac{1}{3} M \overline{v^2}=R T \\ & \overline{v^2}=\frac{3 R}{M} T \\ & \sqrt{\overline{v^2}}=\sqrt{\frac{3 R T}{M}} \\ & v_{r m s}=\sqrt{\frac{3 R T}{M}} \\ & v_{r m s} \propto \sqrt{T}\end{aligned}$

Thus, the root mean square speed of the molecules of a gas is directly proportional to the square root of the absolute temperature of the gas.

Relation between temperature and molecular kinetic energy:-

$
\frac{1}{2} M \overline{v^2}=\frac{1}{2} M\left(\frac{3 R T}{M}\right)
$

• Average kinetic energy of 1 mole of gas $=\frac{3}{2} R T$
• Average kinetic energy of one molecule =

$\frac{(3 / 2) R T}{N}=\frac{3}{2}\left(\frac{R}{N}\right) T$

R/N = k (Boltzmann constant)

$
\text { Average kinetic energy of } 1 \text { molecule }=\frac{3}{2} K T
$

It means different gases at the same temperature have the same average kinetic energy per molecule, and this energy is directly proportional to the absolute temperature of the gas.

Law of Equipartition of Energy

• It states that the total kinetic energy of a dynamical system consisting of a large number of particles in thermal equilibrium is equally distributed among all degrees of freedom, 0.5KT, and the energy associated with each degree of freedom is where k is the Boltzmann constant and T is the absolute temperature of the system.

Thus, the average kinetic energy of a molecule per degree of freedom is 0.5KT, which is the law of equipartition of energy.

Explanation of Gas Laws from Kinetic Theory

1. Boyle’s Law

We know

$P V=\frac{1}{3} m N v^{\overline{2}} \quad \ldots .(i)$

According to kinetic theory, the average kinetic energy of translation of molecules of a gas is directly proportional to its absolute temperature,

$\frac{1}{2} m \overline{v^2}=\alpha T$

i.e., at a given temperature, the average kinetic energy of a gas is constant and N is also constant, so eqn (i)

$P V=\frac{2}{3} N \cdot \frac{1}{2} m \overline{v^2}=\frac{2}{3} N \alpha T$

= constant at a given temperature

This is Boyle's Law.

2. Charles’s Law

From eqn(i)

$P V=\frac{1}{3} m N \overline{v^2}$

Also, the average K.E. of a molecule,

$\begin{aligned} & \frac{1}{2} m \overline{v^2}=\alpha T \\ & P V=\frac{2}{3} N \cdot \alpha T \\ & V \propto T\end{aligned}$

for a constant value P.

Thus, at a given pressure for a given mass of a gas, the volume is directly proportional to the absolute temperature. This is Charles' law.

Mean Free Path

• The average distance traversed by a molecule between two successive collisions is defined as the mean free path.

Thus, if λ₁, λ₂, λ₃, ….λₙ are the successive free paths traversed in the total time t, then,

$\lambda_1+\lambda_2+\ldots . \lambda_n=\bar{v} t$

• If N is the total no. of collisions suffered, then

$\begin{aligned} \lambda & =\frac{\lambda_1+\lambda_2+\lambda_3+\ldots . \lambda_n}{N} \\ & =\frac{\bar{v} t}{N}\end{aligned}$

• Expression for Mean Free Path

We know that,

$\begin{aligned} \lambda & =\frac{\text { total dis } \tan \text { ce covered in time } t}{\text { number of collision in time } t} \\ & =\frac{\bar{v} t}{n \times \pi d^2 \bar{v} t}=\frac{1}{\pi n d^2}\end{aligned}$

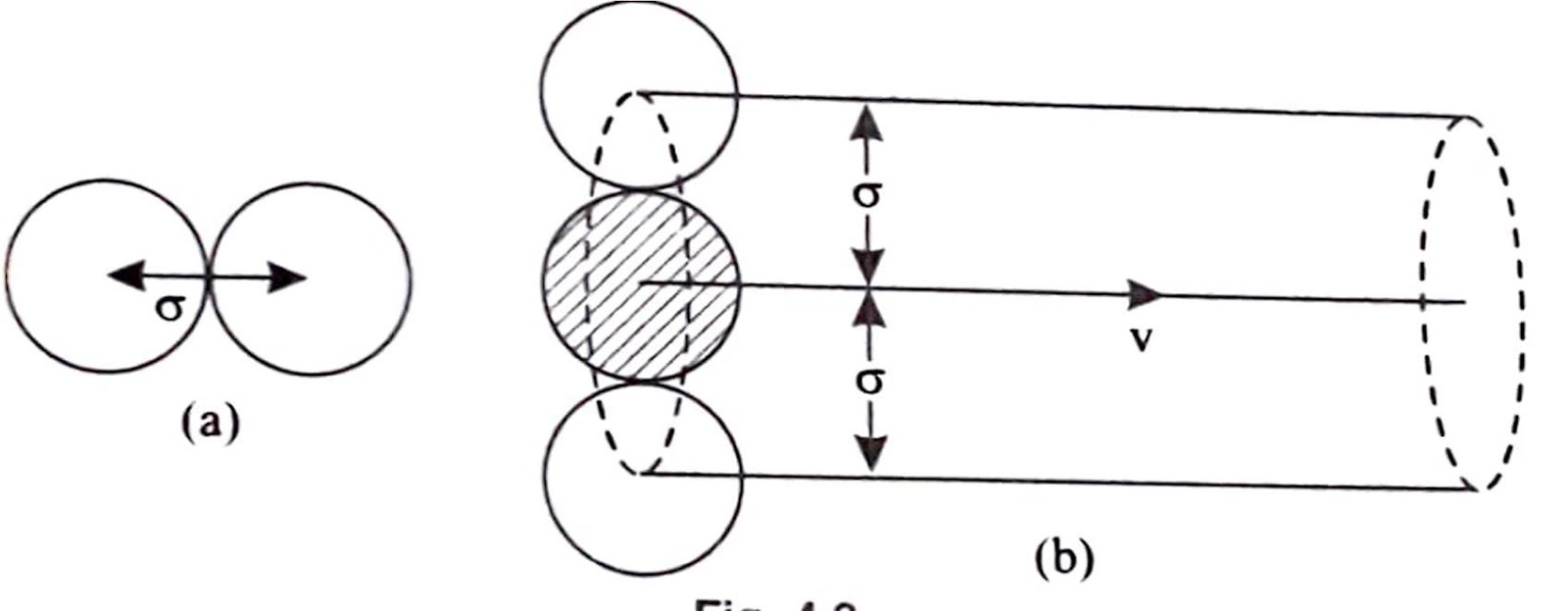
But by experiment, Maxwell found that

$\lambda=\frac{1}{\sqrt{2}\left(\pi \sigma^2 n\right)}$

The mean free path is inversely proportional to the number of molecules per unit volume (n), which is proportional to the density of the gas.

For N molecules of an ideal gas, we have

$\begin{aligned} & P V=N k T \\ & \therefore n=\frac{N}{V}=\frac{P}{k T} \\ & \lambda=\frac{k T}{\sqrt{2} \pi d^2 P}\end{aligned}$

The mean free path of the molecules of a gas is directly proportional to its absolute temperature and inversely proportional to the pressure of the gas.

Avagadro’s Number: Avagadro’s number is the number of molecules in 1 mole of a substance. It is denoted by N and its value is 6.0221 X 10 ²³.

Class 11 Physics Chapter 12 Kinetic Theory: Previous Year Question and Answer

Q1: Diatomic molecules like hydrogen have energies due to both translational as well as rotational motion. From the equation in kinetic theory PV = $\frac{2}{3}E$ , E is

(a) the total energy per unit volume

(b) only the translational part of energy, because rotational energy is very small compared to the translational energy

(c) only the translational part of the energy, because during collisions with the wall, pressure relates to a change in linear momentum

(d) the translational part of the energy because rotational energies of molecules can be of either sign, and their average over all the molecules is zero

Answer:

As per the kinetic theory of gases, the perpendicular forces exerted by the molecules on the walls while in motion are only responsible for the pressure exerted due to the gas molecules. So, for molecules striking at angles other than 90 degrees, no pressure will be exerted. Hence, in this case, only the translational motion change leads to pressure on the wall. So, PV = $\frac{2}{3}E$, which represents the translational motion part and hence (c) is the correct option.

Q2: When an ideal gas is compressed adiabatically, its temperature rises because the molecules, on average, have more kinetic energy than before. The kinetic energy increases,

(a) because of collisions with the moving parts of the wall only

(b) because of collisions with the entire wall

(c) because the molecules get accelerated in their motion inside the volume

(d) because of the redistribution of energy amongst the molecules

Answer:

The number of collisions per second between the molecules and walls increases, and the mean free path becomes smaller as an ideal gas is compressed. This, in turn, increases the temperature of the gas, which increases the overall kinetic energy of the gas molecules as KE depends on the temperature. Hence, (a) is the correct option.

Q3: In a diatomic molecule, the rotational energy at a given temperature
(a) obeys Maxwell's distribution
(b) have the same value for all molecules
(c) equals the translational kinetic energy for each molecule
(d) is $\left(\frac{2}{3}\right) ^{rd}$ the translational kinetic energy for each molecule

Answer:

If we assume a diatomic molecule along the $z$-axis, its energy along that axis will be zero. The total energy of a diatomic molecule can be expressed as: $E=\frac{1}{2} m v x^2+\frac{1}{2} m v y^2+\frac{1}{2} m v z^2+\frac{1}{2} I x W x^2+\frac{1}{2} I x W y^2$.

The number of independent terms in the expression $=5$. The above expression obeys Maxwell's distribution, as their velocities can be predicted with Maxwell's findings. In this case, for each molecule, 3 translational and 2 rotational energies are associated. So, at any temperature, rotational energy $=\left(\frac{2}{3}\right) ^{rd}$ translational KE

Hence, (a) and (d) are the correct options.

Importance of Kinetic Theory Class 11 Notes

Kinetic Theory of Gases Class 11 Notes is an important part of the knowledge that helps to comprehend the behaviour of gases at the molecular level and the relationship between the temperature and pressure, and the volume of the gas. These notes make complicated theoretical ideas simple by explaining them and providing formulas. They are very useful in enhancing theoretical knowledge and preparing well to pass their CBSE board exams, JEE and NEET.

• Theoretical basis of Thermodynamics: The Kinetic theory of gases forms the basis of explaining thermodynamics. It assists students in relating macroscopic quantities as pressure, temperature and volume to the microscopic action of gas molecules.
• Theory behind Understanding of Gas Laws: These notes provide the derivation and physical meaning of several gas laws (Boyle's law, Charles' law, Avogadro's law, etc.) and enable the students to go beyond memorisation and get into a real understanding.
• Connection between Theory and Reality: The chapter discusses the deviation of real gases from ideal gas behaviou,r providing insight about the practical use in physics, chemistry and engineering.
• Develops Problem-Solving Skills: These notes will enable students to approach numerical problems with molecular speeds, mean free path, and specific heat capacities with a high level of confidence, since they will be shown with the help of clear explanations, formulas, and solved examples.
• Good with Competitive Exam: This chapter has often been asked in the JEE Main, JEE Advanced and NEET, most often in questions that require the use of kinetic interpretation of temperature and degrees of freedom. These are notes that give a specific and brief revision tool for such exams.
• Increases the knowledge of Molecular Motion: The notes describe concepts such as root mean square speed, average speed, and equipartition of energ,y and allow the students to imagine how gas molecules have a random movement.
• Supports Practical Applications: These concepts play a critical role in the explanation of real-world phenomena, including diffusion, gaseous exerted pressure and gaseous behaviour in various thermodynamic processes.
• Makes Revision at the last Minute Easy: The notes are concise, summarising the chapter into major points, vital formulas, and charts, and hence they are the best for quick and effective revision of exams.
• Enhances Analytical Thinking: The association of microscopic motion with macroscopic observations will help students to have logical thinking and analysis skills, which are necessary in more complex studies in physics.

NCERT Class 11 Notes Chapter-Wise

These NCERT Class 11 Physics chapter-wise notes provide students with an organised and simplified study resource for all topics in the syllabus. Designed by subject experts, these notes include key formulas, important definitions, solved examples, and practice questions to help students revise efficiently. They are ideal for quick exam preparation for CBSE board exams as well as for competitive exams like JEE and NEET. Students can access these notes online or download them in PDF format for convenient study anytime, anywhere.

Subject-Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus