Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

Edited By Vishal kumar | Updated on Nov 03, 2023 10:56 AM IST

NCERT Solutions for Class 11 Maths Chapter 4 - Principle of Mathematical Induction Exercise 4.1- Download Free PDF

NCERT Solutions for Class 11 Maths Chapter 4 – Principle of Mathematical Induction Exercise 4.1- NCERT solutions for exercise 4.1 Class 11 Maths Chapter 4 deals with the principle of mathematical induction and related problems. Exercise 4.1 Class 11 Maths deals with how to prove a given mathematical statement using the principle of mathematical induction. NCERT Solutions for Class 11 Maths chapter 4 exercise 4.1 gives an insight into the steps of proving a given statement using the idea of induction. Solving both example questions and Class 11 Maths chapter 4 exercise 4.1 are important to understand the concepts discussed in the chapter. Before starting the Class 11 Maths chapter 4 exercise 4.1 the NCERT book discusses the concept of deduction in brief and introduces what is induction and how induction is different from deduction. Followed by examples and Class 11 Maths chapter 4 exercise 4.1.

This Story also Contains
  1. NCERT Solutions for Class 11 Maths Chapter 4 - Principle of Mathematical Induction Exercise 4.1- Download Free PDF
  2. NCERT Solutions for Class 11 Maths Chapter 4 – Principle of Mathematical Induction Exercise 4.1
  3. Access Principle Of Mathematical Induction Class 11 Chapter 4- Exercise 4.1
  4. Question:1 Prove the following by using the principle of mathematical induction for all :
  5. More About NCERT Solutions for Class 11 Maths Chapter 4 Exercise 4.1
  6. Key Features of 11th Class Maths Exercise 4.1 Answers
  7. NCERT Solutions of Class 11 Subject Wise
  8. Subject Wise NCERT Exampler Solutions
NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction
NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

The NCERT Solutions for Class 11 Maths Exercise 4.1 are expertly crafted to help students overcome challenges in problem-solving. They provide step-by-step explanations and a free PDF version for convenient access, ensuring that students can grasp mathematical concepts effectively and excel in their studies.

Also see-

NCERT Solutions for Class 11 Maths Chapter 4 – Principle of Mathematical Induction Exercise 4.1

Download PDF


Access Principle Of Mathematical Induction Class 11 Chapter 4- Exercise 4.1

Question:1 Prove the following by using the principle of mathematical induction for all n\in N : 1+3+3^2+...+3^{n-1}=\frac{(3^n-1)}{2}

Answer:

Let the given statement be p(n) i.e.
p(n):1+3+3^2+...+3^{n-1}=\frac{(3^n-1)}{2}
For n = 1 we have
p(1): 1=\frac{(3^1-1)}{2}=\frac{3-1}{2}= \frac{2}{2}=1 , which is true

For n = k we have
p(k):1+3+3^2+...+3^{k-1}=\frac{(3^k-1)}{2} \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true

Now,
For n = k + 1 we have
p(k+1):1+3+3^2+...+3^{k+1-1}= 1+3+3^2+...+3^{k-1}+3^{k}
= (1+3+3^2+...+3^{k-1})+3^{k}
= \frac{(3^k-1)}{2}+3^{k} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (Using \ (i))
= \frac{3^k-1+2.3^k}{2}
= \frac{3^k(1+2)-1}{2}
= \frac{3.3^k-1}{2}
= \frac{3^{k+1}-1}{2}
Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:2 Prove the following by using the principle of mathematical induction for all n\in N : 1^3+2^3+3^3+...+n^3=\left (\frac{n(n+1)}{2} \right )^2

Answer:

Let the given statement be p(n) i.e.
p(n):1^3+2^3+3^3+...+n^3=\left (\frac{n(n+1)}{2} \right )^2
For n = 1 we have
p(1):1=\left (\frac{1(1+1)}{2} \right )^2= \left ( \frac{1(2)}{2} \right )^2=(1)^2=1 , which is true

For n = k we have
p(k):1^3+2^3+3^3+...+k^3=\left (\frac{k(k+1)}{2} \right )^2 \ \ \ \ \ \ \ \ \ \ - (i) , Let's assume that this statement is true

Now,
For n = k + 1 we have
p(k+1):1^3+2^3+3^3+...+(k+1)^3=1^3+2^3+3^3+...+k^3+(k+1)^3
=(1^3+2^3+3^3+...+k^3)+(k+1)^3
=\left ( \frac{k(k+1)}{2} \right )^2+(k+1)^3 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{k^2(k+1)^2+4(k+1)^3}{4}
=\frac{(k+1)^2(k^2+4(k+1))}{4}
=\frac{(k+1)^2(k^2+4k+4)}{4}
=\frac{(k+1)^2(k+2)^2}{4} \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because a^2+2ab+b^2=(a+b)^2)
=\left ( \frac{(k+1)(k+2)}{2} \right )^2
Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:3 Prove the following by using the principle of mathematical induction for all n\in N :

1+\frac{1}{(1+2)}+\frac{1}{(1+2+3)}+...+\frac{1}{(1+2+3+...+n)}=\frac{2n}{(n+1)}

Answer:

Let the given statement be p(n) i.e.
p(n):1+\frac{1}{(1+2)}+\frac{1}{(1+2+3)}+...+\frac{1}{(1+2+3+...+n)}=\frac{2n}{(n+1)}
For n = 1 we have
p(1):1=\left (\frac{2(1)}{1+1} \right )= \left ( \frac{2}{2} \right )=1 , which is true

For n = k we have
p(k):1+\frac{1}{(1+2)}+\frac{1}{(1+2+3)}+...+\frac{1}{(1+2+3+...+k)}=\frac{2k}{(k+1)} \ \ \ \ -(i) , Let's assume that this statement is true

Now,
For n = k + 1 we have
p(k+1):1+\frac{1}{(1+2)}+\frac{1}{(1+2+3)}+...+\frac{1}{(1+2+3+...+k+1)} =\left ( 1+\frac{1}{(1+2)}+\frac{1}{(1+2+3)}+...+\frac{1}{(1+2+3+...+k)} \right )+\frac{1}{(1+2+3+...+k+k+1)}

=\frac{2k}{k+1}+\frac{1}{(1+2+3+...+k+(k+1))} \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{2k}{k+1}+\frac{1}{\frac{(k+1)(k+1+1)}{2}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because1+2+....+n = \frac{n(n+1)}{2} )
=\frac{2k}{k+1}+\frac{2}{(k+1)(k+2)}
=\frac{2}{k+1}\left (k+\frac{1}{k+2} \right )
=\frac{2}{k+1}\left ( \frac{k^2+2k+1}{k+2} \right )
=\frac{2}{k+1}.\frac{(k+1)^2}{k+2}
=\frac{2(k+1)}{k+2}
Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:4 Prove the following by using the principle of mathematical induction for all n\in N : 1.2.3+2.3.4+...+n(n+1)(n+2)=\frac{n(n+1)(n+2)(n+3)}{4}

Answer:

Let the given statement be p(n) i.e.
p(n):1.2.3+2.3.4+...+n(n+1)(n+2)=\frac{n(n+1)(n+2)(n+3)}{4}
For n = 1 we have
p(1):6=\left (\frac{1(1+1)(1+2)(1+3)}{4} \right )= \left ( \frac{1.2.3.4}{4} \right )=6 , which is true

For n = k we have
p(k):1.2.3+2.3.4+...+k(k+1)(k+2)=\frac{k(k+1)(k+2)(k+3)}{4} \ \ \ \ \ \ -(i) , Let's assume that this statement is true

Now,
For n = k + 1 we have
p(k+1):1.2.3+2.3.4+...+k(k+1)(k+2) + (k+1)(k+2)(k+3) =(1.2.3+2.3.4+...+k(k+1)(k+2)) + (k+1)(k+2)(k+3)

=\frac{k(k+1)(k+2)(k+3)}{4} + (k+1)(k+2)(k+3) \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{k(k+1)(k+2)(k+3)+4(k+1)(k+2)(k+3) }{4}
=\frac{(k+1)(k+2)(k+3)(k+4) }{4}
Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:5 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : 1.3+2.3^2+3.3^3+...+n.3^n=\frac{(2n-1)3^{n+1}+3}{4}

Answer:

Let the given statement be p(n) i.e.
p(n):1.3+2.3^2+3.3^3+...+n.3^n=\frac{(2n-1)3^{n+1}+3}{4}
For n = 1 we have
p(1):3=\frac{(2(1)-1)3^{1+1}+3}{4}= \frac{(2-1)9+3}{4}=\frac{12}{4}=3 , which is true

For n = k we have

p(k):1.3+2.3^2+3.3^3+...+k.3^k=\frac{(2k-1)3^{k+1}+3}{4} \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):1.3+2.3^2+3.3^3+...+(k+1).3^{(k+1)}=1.3+2.3^2+3.3^3+...+k.3^k+(k+1).3^{(k+1)}

=\frac{(2k-1)3^{k+1}+3}{4}+(k+1).3^{(k+1)}
=\frac{(2k-1)3^{k+1}+3+4(k+1).3^{(k+1)}}{4}
=\frac{3^{k+1}((2k-1)+4(k+1))+3}{4}
=\frac{3^{k+1}(6k+3)+3}{4}
=\frac{3^{k+1}.3(2k+1)+3}{4}
=\frac{(2k+1)3^{k+2}+3}{4}
=\frac{(2(k+1)-1)3^{(k+1)+1}+3}{4}
Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:6 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : 1.2+2.3+3.4+...+n.(n+1)=\left [\frac{n(n+1)(n+2)}{3} \right ]

Answer:

Let the given statement be p(n) i.e.
p(n):1.2+2.3+3.4+...+n.(n+1)=\left [\frac{n(n+1)(n+2)}{3} \right ]
For n = 1 we have
p(1):2=\left [\frac{1(1+1)(1+2)}{3} \right ]= \frac{1.2.3}{3}=2 , which is true

For n = k we have

p(k):1.2+2.3+3.4+...+k.(k+1)=\left [\frac{k(k+1)(k+2)}{3} \right ] \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):1.2+2.3+3.4+...+(k+1).(k+2)=1.2+2.3+3.4+...+k(k+1)+(k+1).(k+2)

=\frac{k(k+1)(k+2)}{3}+(k+1).(k+2) \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{k(k+1)(k+2)+3(k+1).(k+2)}{3}
=\frac{(k+1)(k+2)(k+3)}{3}
=\frac{(k+1)(k+1+1)(k+1+2)}{3}

Thus, p(k+1) is true whenever p(k) is true
Hence, by principle of mathematical induction , statement p(n) is true for all natural numbers n

Question:7 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : 1.3+3.5+5.7+...+(2n-1)(2n+1)=\frac{n(4n^2+6n-1)}{3}

Answer:

Let the given statement be p(n) i.e.
p(n):1.3+3.5+5.7+...+(2n-1)(2n+1)=\frac{n(4n^2+6n-1)}{3}
For n = 1 we have
p(1):1.3=3=\frac{1(4(1)^2+6(1)-1)}{3}= \frac{4+6-1}{3}=\frac{9}{3}=3 , which is true

For n = k we have

p(k):1.3+3.5+5.7+...+(2k-1)(2k+1)=\frac{k(4k^2+6k-1)}{3} \ \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):1.3+3.5+5.7+...+(2(k+1)-1)(2(k+1)+1)=1.3+3.5+5.7+...+(2k-1)(2k+1)+(2(k+1)-1)(2(k+1)+1)

=\frac{k(4k^2+6k-1)}{3}+(2k+1)(2k+3) \ \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{k(4k^2+6k-1)+3(2k+1)(2k+3)}{3}
=\frac{k(4k^2+6k-1)+3(4k^2+8k+3)}{3}
=\frac{(4k^3+6k^2-k+12k^2+28k+9)}{3}
=\frac{(4k^3+18k^2+23k+9)}{3}
=\frac{(4k^3+14k^2+9k+4k^2+14k+9)}{3}
=\frac{(k(4k^2+14k+9)+4k^2+14k+9)}{3}
=\frac{(4k^2+14k+9)(k+1)}{3}
=\frac{(k+1)(4k^2+8k+4+6k+6-1)}{3}
=\frac{(k+1)(4(k^2+2k+1)+6(k+1)-1)}{3}
=\frac{(k+1)(4(k+1)^2+6(k+1)-1)}{3}

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:8 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : 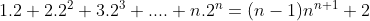1.2+2.2^2+3.2^3+....+n.2^n=(n-1)n^{n+1}+2

Answer:

Let the given statement be p(n) i.e.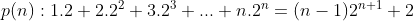
p(n):1.2+2.2^2+3.2^3+...+n.2^n=(n-1)2^{n+1}+2
For n = 1 we have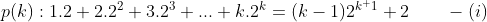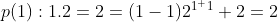p(k):1.2+2.2^2+3.2^3+...+k.2^k=(k-1)2^{k^+1}+2 \ \ \ \ \ \ -(i)p(1):1.2=2=(1-1)2^{1^+1}+2 = 2 , which is true

For n = k we have

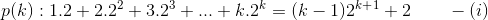
p(k):1.2+2.2^2+3.2^3+...+k.2^k=(k-1)2^k^+^1+2 \ \ \ \ \ \ -(i)

, Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):1.2+2.2^2+3.2^3+...+(k+1).2^{k+1} =1.2+2.2^2+3.2^3+...+k.2^k+(k+1).2^{k+1}

=(k-1)2^{k+1}+2+(k+1).2^{k+1} \ \ \ \ \ \ \ \ \ \ (using \ (i))
=2^{k+1}(k-1+k+1)+2
=2^{k+1}(2k)+2
=k.2^{k+2}+2
=(k+1-1).2^{k+1+1}+2

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:9 Prove the following by using the principle of mathematical induction for all n\in\mathbb{N} : \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^n}=1-\frac{1}{2^n}

Answer:

Let the given statement be p(n) i.e.
p(n):\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^n}=1-\frac{1}{2^n}
For n = 1 we have
p(1):\frac{1}{2}=1-\frac{1}{2^1}= 1-\frac{1}{2} = \frac{1}{2} , which is true

For n = k we have

p(k):\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^k}=1-\frac{1}{2^k} \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^{k+1}}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^k}+\frac{1}{2^{k+1}}

=1-\frac{1}{2^k}+\frac{1}{2^{k+1}} \ \ \ \ \ \ \ \ \ \ (using \ (i))
=1-\frac{1}{2^k}\left (1-\frac{1}{2} \right )
=1-\frac{1}{2^k}\left (\frac{1}{2} \right )
=1-\frac{1}{2^{k+1}}

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:10 Prove the following by using the principle of mathematical induction for all n\in\mathbb{N} : \frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{(3n-1)(3n+2)}=\frac{n}{(6n+4)}

Answer:

Let the given statement be p(n) i.e.
p(n):\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{(3n-1)(3n+2)}=\frac{n}{(6n+4)}
For n = 1 we have
p(1):\frac{1}{2.5}= \frac{1}{10}=\frac{1}{(6(1)+4)}= \frac{1}{10} , which is true

For n = k we have

p(k):\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{(3k-1)(3k+2)}=\frac{k}{(6k+4)} \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{(3(k+1)-1)(3(k+1)+2)}=\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{(3k-1)(3k+2)}+\frac{1}{(3(k+1)-1)(3(k+1)+2)}

=\frac{k}{6k+4}+\frac{1}{(3k+2)(3k+5)} \ \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{1}{3k+2}\left ( \frac{k}{2}+\frac{1}{3k+5} \right )
=\frac{1}{3k+2}\left ( \frac{k(3k+5)+2}{2(3k+5)} \right )
=\frac{1}{3k+2}\left ( \frac{3k^2+5k+2}{2(3k+5)} \right )
=\frac{1}{3k+2}\left ( \frac{3k^2+3k+2k+2}{2(3k+5)} \right )
=\frac{1}{3k+2}\left ( \frac{(3k+2)(k+1)}{2(3k+5)} \right )
=\frac{(k+1)}{6k+10}
=\frac{(k+1)}{6(k+1)+4}

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:11 Prove the following by using the principle of mathematical induction for all n\in\mathbb{N} : \frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{n(n+1)(n+2)}=\frac{n(n+3)}{4(n+1)(n+2)}

Answer:

Let the given statement be p(n) i.e.
p(n):\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{n(n+1)(n+2)}=\frac{n(n+3)}{4(n+1)(n+2)}
For n = 1 we have
p(1):\frac{1}{1.2.3}=\frac{1}{6}=\frac{1(1+3)}{4(1+1)(1+2)}=\frac{4}{4.2.3}=\frac{1}{6} , which is true

For n = k we have

p(k):\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{k(k+1)(k+2)}=\frac{k(k+3)}{4(k+1)(k+2)} \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{(k+1)(k+2)(k+3)}=\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{k(k+1)(k+2)}+\frac{1}{(k+1)(k+2)(k+3)}

=\frac{k(k+3)}{4(k+1)(k+2)}+\frac{1}{(k+1)(k+2)(k+3)} \ \ \ \ \ \ (using \ (i))
=\frac{1}{(k+1)(k+2)}\left ( \frac{k(k+3)}{4}+ \frac{1}{k+3} \right )
=\frac{1}{(k+1)(k+2)}\left ( \frac{k(k+3)^2+4}{4(k+3)} \right )
=\frac{1}{(k+1)(k+2)}\left ( \frac{k(k^2+9+6k)+4}{4(k+3)} \right )
=\frac{1}{(k+1)(k+2)}\left ( \frac{k^3+9k+6k^2+4}{4(k+3)} \right )
=\frac{1}{(k+1)(k+2)}\left ( \frac{k^3+2k^2+k+8k+4k^2+4}{4(k+3)} \right )
=\frac{1}{(k+1)(k+2)}\left ( \frac{k(k^2+2k+1)+4(k^2+2k+1)}{4(k+3)} \right )
=\frac{1}{(k+1)(k+2)}\left ( \frac{(k+1)^2(k+4)}{4(k+3)} \right )
= \frac{(k+1)((k+1)+3)}{4(k+1+1)(k+1+2)}

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:12 Prove the following by using the principle of mathematical induction for all n\in\mathbb{N} : a+ar+ar^2+...+ar^{n-1}=\frac{a(r^n-1)}{r-1}

Answer:

Let the given statement be p(n) i.e.
p(n):a+ar+ar^2+...+ar^{n-1}=\frac{a(r^n-1)}{r-1}
For n = 1 we have
p(1):a=\frac{a(r^1-1)}{r-1}=\frac{r-1}{r-1}=1 , which is true

For n = k we have

p(k):a+ar+ar^2+...+ar^{k-1}=\frac{a(r^k-1)}{r-1} \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):a+ar+ar^2+...+ar^{k}=a+ar+ar^2+...+ar^{k-1}+ar^{k}

=a.\frac{r^k-1}{r-1}+ar^{k} \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{a(r^k-1)+(r-1)ar^{k}}{r-1}
=\frac{ar^k(1+r-1)-a}{r-1}
=\frac{ar^k.r-a}{r-1}
=\frac{a(r^{k+1}-1)}{r-1}

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:13 Prove the following by using the principle of mathematical induction for all n\in\mathbb{N} : \left ( 1+\frac{3}{1} \right )\left ( 1+\frac{5}{4} \right )\left ( 1+\frac{7}{9} \right )..\left ( 1+\frac{(2n+1)}{n^2} \right )=(n+1)^2

Answer:

Let the given statement be p(n) i.e.
p(n):\left ( 1+\frac{3}{1} \right )\left ( 1+\frac{5}{4} \right )\left ( 1+\frac{7}{9} \right )..\left ( 1+\frac{(2n+1)}{n^2} \right )=(n+1)^2
For n = 1 we have
p(1):\left ( 1+\frac{3}{1} \right )= 4=(1+1)^2=2^2=4 , which is true

For n = k we have

p(k):\left ( 1+\frac{3}{1} \right )\left ( 1+\frac{5}{4} \right )\left ( 1+\frac{7}{9} \right )..\left ( 1+\frac{(2k+1)}{k^2} \right )=(k+1)^2 \ \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):\left ( 1+\frac{3}{1} \right )\left ( 1+\frac{5}{4} \right )\left ( 1+\frac{7}{9} \right )..\left ( 1+\frac{(2(k+1)+1)}{(k+1)^2} \right ) =\left ( 1+\frac{3}{1} \right )\left ( 1+\frac{5}{4} \right )\left ( 1+\frac{7}{9} \right )..\left ( 1+\frac{2k+1}{k^2} \right )\left ( 1+\frac{(2(k+1)+1)}{(k+1)^2} \right )

=(k+1)^2\left ( 1+\frac{(2(k+1)+1)}{(k+1)^2} \right ) \ \ \ \ \ \ \ \ \ \ (using \ (i))
=(k+1)^2\left ( \frac{{}(k+1)^2+(2(k+1)+1)}{(k+1)^2} \right )
=(k^2+1+2k+2k+2+1)
=(k^2+4k+4)
=(k+2)^2
=(k+1+1)^2

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:14 Prove the following by using the principle of mathematical induction for all n\in\mathbb{N} : \left ( 1+\frac{1}{1} \right )\left ( 1+\frac{1}{2} \right )\left ( 1+\frac{1}{3} \right )...\left ( 1+\frac{1}{n} \right )=(n+1)

Answer:

Let the given statement be p(n) i.e.
p(n):\left ( 1+\frac{1}{1} \right )\left ( 1+\frac{1}{2} \right )\left ( 1+\frac{1}{3} \right )...\left ( 1+\frac{1}{n} \right )=(n+1)
For n = 1 we have
p(1):\left ( 1+\frac{1}{1} \right )=2=(1+1)=2 , which is true

For n = k we have

p(k):\left ( 1+\frac{1}{1} \right )\left ( 1+\frac{1}{2} \right )\left ( 1+\frac{1}{3} \right )...\left ( 1+\frac{1}{k} \right )=(k+1) \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):\left ( 1+\frac{1}{1} \right )\left ( 1+\frac{1}{2} \right )\left ( 1+\frac{1}{3} \right )...\left ( 1+\frac{1}{k+1} \right ) &nbsnbsp; =\left ( 1+\frac{1}{1} \right )\left ( 1+\frac{1}{2} \right )\left ( 1+\frac{1}{3} \right )...\left ( 1+\frac{1}{k} \right )\left ( 1+\frac{1}{k+1} \right )

=(k+1)\left ( 1+\frac{1}{k+1} \right ) \ \ \ \ \ \ \ (using \ (i))
=(k+1)\left ( \frac{k+1+1}{k+1} \right )
=(k+2)
=(k+1+1)
Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:15 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : 1^2+3^2+5^2+...+(2n-1)^2=\frac{n(2n-1)(2n+1)}{3}

Answer:

Let the given statement be p(n) i.e.
p(n):1^2+3^2+5^2+...+(2n-1)^2=\frac{n(2n-1)(2n+1)}{3}
For n = 1 we have
p(1):1^2=1=\frac{1(2(1)-1)(2(1)+1)}{3}= \frac{1.1.3}{3}=1 , which is true

For n = k we have

p(k):1^2+3^2+5^2+...+(2k-1)^2=\frac{k(2k-1)(2k+1)}{3} \ \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):1^2+3^2+5^2+...+(2(k+1)-1)^2=1^2+3^2+5^2+...+(2k-1)^2+(2(k+1)-1)^2

=\frac{k(2k-1)(2k+1)}{3}+(2(k+1)-1)^2 \ \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{k(2k-1)(2k+1)+3(2(k+1)-1)^2}{3}
=\frac{k(2k-1)(2k+1)+3(2k+1)^2}{3}
=\frac{(2k+1)(k(2k-1)+3(2k+1))}{3}
=\frac{(2k+1)(2k^2-k+6k+3)}{3}
=\frac{(2k+1)(2k^2+5k+3)}{3}
=\frac{(2k+1)(2k^2+2k+3k+3)}{3}
=\frac{(2k+1)(2k+3)(k+1)}{3}
=\frac{(k+1)(2(k+1)-1)(2(k+1)+1)}{3}

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:16 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : \frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+...+\frac{1}{(3n-2)(3n+1)}=\frac{n}{(3n+1)}

Answer:

Let the given statement be p(n) i.e.
p(n):\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+...+\frac{1}{(3n-2)(3n+1)}=\frac{n}{(3n+1)}
For n = 1 we have
p(1):\frac{1}{1.4}=\frac{1}{4}=\frac{1}{(3(1)+1)}=\frac{1}{3+1}=\frac{1}{4} , which is true

For n = k we have

p(k):\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+...+\frac{1}{(3k-2)(3k+1)}=\frac{k}{(3k+1)} \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+...+\frac{1}{(3(k+1)-2)(3(k+1)+1)}=\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+...+\frac{1}{(3k-2)(3k+1)}+\frac{1}{(3(k+1)-2)(3(k+1)+1)}

=\frac{k}{3k+1}+\frac{1}{(3k+1)(3k+4)} \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{1}{3k+1}\left ( k+\frac{1}{3k+4} \right )
=\frac{1}{3k+1}\left ( \frac{k(3k+4)+1}{3k+4} \right )
=\frac{1}{3k+1}\left ( \frac{3k^2+4k+1}{3k+4} \right )
=\frac{1}{3k+1}\left ( \frac{3k^2+3k+k+1}{3k+4} \right )
=\frac{1}{3k+1}\left ( \frac{(3k+1)(k+1)}{3k+4} \right )
= \frac{(k+1)}{3k+4}
= \frac{(k+1)}{3(k+1)+1}

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:17 Prove the following by using the principle of mathematical induction for all n\in N : \frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+...+\frac{1}{(2n+1)(2n+3)}=\frac{n}{3(2n+3)}

Answer:

Let the given statement be p(n) i.e.
p(n):\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+...+\frac{1}{(2n+1)(2n+3)}=\frac{n}{3(2n+3)}
For n = 1 we have
p(1):\frac{1}{3.5}= \frac{1}{15}=\frac{1}{3(2(1)+3)}=\frac{1}{3.5}=\frac{1}{15} , which is true

For n = k we have

p(k):\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+...+\frac{1}{(2k+1)(2k+3)}=\frac{k}{3(2k+3)} \ \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+...+\frac{1}{(2(k+1)+1)(2(k+1)+3)}=\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+...+\frac{1}{(2k+1)(2k+3)}+\frac{1}{(2(k+1)+1)(2(k+1)+3)}

=\frac{k}{3(2k+3)}+\frac{1}{(2k+3)(2k+5)} \ \ \ \ \ \ \ \ \ \ (using \ (i))
=\frac{1}{2k+3}\left ( \frac{k}{3}+\frac{1}{2k+5} \right )
=\frac{1}{2k+3}\left ( \frac{k(2k+5)+3}{3(2k+5)} \right )
=\frac{1}{2k+3}\left ( \frac{2k^2+5k+3}{3(2k+5)} \right )
=\frac{1}{2k+3}\left ( \frac{2k^2+2k+3k+3}{3(2k+5)} \right )
=\frac{1}{2k+3}\left ( \frac{(2k+3)(k+1)}{3(2k+5)} \right )
= \frac{(k+1)}{3(2k+5)}
= \frac{(k+1)}{3(2(k+1)+3)}

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:18 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : 1+2+3+...+n<\frac{1}{8}(2n+1)^2.

Answer:

Let the given statement be p(n) i.e.
p(n):1+2+3+...+n<\frac{1}{8}(2n+1)^2.
For n = 1 we have
p(1):1<\frac{1}{8}(2(1)+1)^2= \frac{1}{8}(3)^2=\frac{9}{8} , which is true

For n = k we have

p(k):1+2+3+...+k<\frac{1}{8}(2k+1)^2 \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this statement is true
Now,
For n = k + 1 we have
p(k+1):1+2+3+...+k+1=1+2+3+...+k+k+1

< \frac{1}{8}\left ( 2k+1 \right )^2+(k+1) \ \ \ \ \ \ \ \ \ (using \ (i))
< \frac{1}{8}\left ( (2k+1)^2+8(k+1) \right )
< \frac{1}{8}\left ( 4k^2+4k+1+8k+8 \right )
< \frac{1}{8}\left ( 4k^2+12k+9\right )
< \frac{1}{8}\left ( 2k+3\right )^2
< \frac{1}{8}\left ( 2(k+1)+1\right )^2

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

Question:19 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : n(n+1)(n+5) is a multiple of 3.

Answer:

Let the given statement be p(n) i.e.
p(n):n(n+1)(n+5)
For n = 1 we have
p(1):1(1+1)(1+5)=1.2.6=12 , which is multiple of 3, hence true

For n = k we have

p(k):k(k+1)(k+5) \ \ \ \ \ \ \ -(i) , Let's assume that this is multiple of 3 = 3m
Now,
For n = k + 1 we have
p(k+1):(k+1)((k+1)+1)((k+1)+5)=(k+1)(k+2)((k+5)+1)

=(k+1)(k+2)(k+5)+(k+1)(k+2)
=k(k+1)(k+5)+2(k+1)(k+5)+(k+1)(k+2)
=3m+2(k+1)(k+5)+(k+1)(k+2) \ \ \ \ \ \ \ \ (using \ (i))
=3m+(k+1)(2(k+5)+(k+2)) \ \ \ \ \ \ \ \ (using \ (i))
=3m+(k+1)(2k+10+k+2)
=3m+(k+1)(3k+12)
=3m+3(k+1)(k+4)
=3(m+(k+1)(k+4) )
=3l Where \left ( l=(m+(k+1)(k+4) ) \right ) some natural number

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is multiple of 3 for all natural numbers n

Question:20 Prove the following by using the principle of mathematical induction for all n\in N : 10^{2n-1}+1 is a divisible by 11.

Answer:

Let the given statement be p(n) i.e.
p(n):10^{2n-1}+1
For n = 1 we have
p(1):10^{2(1)-1}+1= 10^{2-1}+1=10^1+1=11 , which is divisible by 11, hence true

For n = k we have

p(k):10^{2k-1}+1 \ \ \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this is divisible by 11 = 11m
Now,
For n = k + 1 we have
p(k+1):10^{2(k+1)-1}+1=10^{2k+2-1}+1
nbsp;
=10^{2k+1}+1
=10^2(10^{2k-1}+1-1)+1
=10^2(10^{2k-1}+1)-10^2+1
=10^2(11m)-100+1 \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
=100(11m)-99
=11(100m-9)
=11l Where l= (100m-9) some natural number

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is divisible by 11 for all natural numbers n

Question:21 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : x^2^n-y^2^n is divisible by x+y.

Answer:

Let the given statement be p(n) i.e.
p(n):x^2^n-y^2^n
For n = 1 we have
p(1):x^{2(1)}-y^{2(1)}= x^2-y^2=(x-y)(x+y) , which is divisible by (x+y) , hence true (using \ a^2-b^2=(a+b)(a-b))

For n = k we have

p(k):x^{2k}-y^{2k} \ \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this is divisible by (x+y) =(x+y)m
Now,
For n = k + 1 we have
p(k+1):x^{2(k+1)}-y^{2(k+1)} =x^{2k}.x^2-y^{2k}.y^2

=x^2(x^{2k}+y^{2k}-y^{2k})-y^{2k}.y^2
=x^2(x^{2k}-y^{2k})+x^2.y^{2k}-y^{2k}.y^2
=x^2(x+y)m+(x^2-y^2)y^{2k} \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
=x^2(x+y)m+((x-y)(x+y))y^{2k} \ \ \ \ \ \ \ \ \ \ \ \ (using \ a^2-b^2=(a+b)(a-b))
=(x+y)\left ( x^2.m+(x-y).y^{2k} \right )
=(x+y)l where l = (x^2.m+(x-y).y^{2k}) some natural number

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is divisible by (x+y) for all natural numbers n

Question:22 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : 3^{2n+2}-8n-9 is divisible by 8.

Answer:

Let the given statement be p(n) i.e.
p(n):3^{2n+2}-8n-9
For n = 1 we have
p(1):3^{2(1)+2}-8(1)-9= 3^4-8-9=81-17=64=8\times 8 , which is divisible by 8, hence true

For n = k we have

p(k):3^{2k+2}-8k-9 \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this is divisible by 8 = 8m
Now,
For n = k + 1 we have
p(k+1):3^{2(k+1)+2}-8(k+1)-9=3^{2k+2+2}-8(k+1)-9
=3^{2k+2}.3^2-8k-8-9
=3^2(3^{2k+2}-8k-9+8k+9)-8k-17
=3^2(3^{2k+2}-8k-9)+3^2(8k+9)-8k-17
=9\times 8m+9(8k+9)-8k-17 \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
=9\times 8m+72k+81-8k-17
=9\times 8m+80k-64
=9\times 8m+8(10k-8)
=8(9m+10k-8)
=8l where l= 9m+10k-8 some natural number

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is divisible by 8 for all natural numbers n

Question:23 Prove the following by using the principle of mathematical induction for all n\in\mathbb{N} : 41^n-14^n is a multiple of 27.

Answer:

Let the given statement be p(n) i.e.
p(n):41^n-14^n
For n = 1 we have
p(1):41^1-14^1= 41-14= 27 , which is divisible by 27, hence true

For n = k we have

p(k):41^k-14^k \ \ \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this is divisible by 27 = 27m
Now,
For n = k + 1 we have
p(k+1):41^{k+1}-14^{k+1}=41^{k}.41-14^{k}.14
=41(41^{k}-14^k+14^k)-14^{k}.14
=41(41^{k}-14^k)+14^k.41-14^{k}.14
=41(27m)+14^k(41-14) \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
=41(27m)+14^k.27
=27(41m+14^k)
=27l where l = 41m+14^k some natural number

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is divisible by 27 for all natural numbers n

Question:24 Prove the following by using the principle of mathematical induction for all n\in \mathbb{N} : (2n+7)<(n+3)^2

Answer:

Let the given statement be p(n) i.e.
p(n):(2n+7)<(n+3)^2
For n = 1 we have
p(1):(2(1)+7)<(1+3)^2\Rightarrow 9< 16 , which is true

For n = k we have

p(k):(2k+7)<(k+3)^2 \ \ \ \ \ \ \ \ \ \ \ -(i) , Let's assume that this is true
Now,
For n = k + 1 we have
p(k+1):(2(k+1)+7)=(2k+2+7)
<(k+3)^2+2 \ \ \ \ \ \ \ \ \ \ \ (using \ (i))
<k^2+9+6k+2
<k^2+6k+11
Now , \ <k^2+6k+11<k^2+8k+16
<(k+4)^2
<((k+1)+3)^2

Thus, p(k+1) is true whenever p(k) is true
Hence, by the principle of mathematical induction, statement p(n) is true for all natural numbers n

More About NCERT Solutions for Class 11 Maths Chapter 4 Exercise 4.1

Before the introduction of exercise 4.1 Class 11 Maths 8 example problems are given in NCERT chapter 4 of Class 11. Only one exercise is discussed in this chapter, which is Class 11 Maths chapter 4 exercise 4.1. 24 questions are discussed in the Class 11 Maths chapter 4 exercise 4.1. Solving all these questions are important as students may face similar or same questions in the exam paper. Give a good number of try to solve questions before looking to the NCERT solutions for Class 11 Maths chapter 4 exercise 4.1.

Also Read| Principle Of Mathematical Induction Class 11th Notes

Benefits of NCERT Solutions for Class 11 Maths Chapter 4 Exercise 4.1

  • Solving all the questions of exercise 4.1 Class 11 Maths gives a good idea of the steps involved in solving a given problem using mathematical induction

  • From this 11th class maths exercise 4.1 answers, students can definitely expect a question for the Class 11 final exam. To solve questions in the exam paper it is important to practice NCERT solutions for Class 11 Maths chapter 4 exercise 4.1.

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Key Features of 11th Class Maths Exercise 4.1 Answers

  1. Step-by-step explanations: Detailed ex 4.1 class 11 solutions with a step-by-step breakdown for each problem.

  2. Clarity and precision: Clear and accurate presentation, helping students confidently prepare for exams.

  3. Conceptual understanding: Emphasis on fostering a deep understanding of mathematical concepts.

  4. Curriculum alignment: class 11 maths ex 4.1 solutions closely follow the NCERT curriculum, covering topics as per the official syllabus.

  5. Variety of practice problems: A range of class 11 maths chapter 4 exercise 4.1 exercises provided for students to enhance their problem-solving skills.

  6. Accessibility: Class 11 ex 4.1 solutions are often available for free, making them easily accessible to students.

  7. Format options: PDF versions are typically offered for convenient online and offline access.

NCERT Solutions of Class 11 Subject Wise

Subject Wise NCERT Exampler Solutions

Frequently Asked Question (FAQs)

1. How many topics are given in the NCERT Class 11 chapter 4?

Three topics

2. What are the three topics given in the chapter principle of mathematical induction?

Introduction, motivation and the principle of mathematical induction

3. How many questions are solved in the Class 11 Maths chapter 4 exercise 4.1?

24 questions

4. What number of solved examples are given in the NCERT Class 11 Maths Chapter 4 - Principle of Mathematical Induction?

Eight examples are solved before the Exercise 4.1 Class 11 Maths

5. What is the relation between the principle of mathematical induction and Peano’s axioms?

It is a restatement of one of Peano’s axioms

6. Who was the first person to name and define mathematical induction?

De Morgan

7. Which mathematician is credited with the origin of the principle of mathematical induction?

Blaise Pascal

8. Why do we solve NCERT Solutions for Class 11 Maths chapter 4 exercise 4.1?

The basic aim of solving the NCERT exercise is to understand the concepts well and to get an insight in to different types of questions that uses the concepts studied. Other than this Class 11th Maths chapter 4 exercise 4.1 will help in exams also. 

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:15 July,2024 - 14 August,2024

National Institute of Open Schooling 12th Examination

Late Fee Application Date:22 July,2024 - 31 July,2024

National Institute of Open Schooling 10th examination

Late Fee Application Date:22 July,2024 - 31 July,2024

Chhattisgarh Board of Secondary Education 12th Examination

Exam Date:23 July,2024 - 12 August,2024

Chhattisgarh Board of Secondary Education 10th Examination

Exam Date:24 July,2024 - 08 August,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

PTE Exam 2024 Registrations
PTE Exam 2024 Registrations
Apply

Register now for PTE & Save 5% on English Proficiency Tests with ApplyShop Gift Cards

View All Application Forms
News and Notifications
Arunachal Pradesh government to create school clusters for optimization of educational resources
eVidyaloka, Indian Army collaborate to set up digital classroom in Jammu and Kashmir
Dehradun: Schools, anganwadi centres to remain closed today amid heavy rain alert
President Droupadi Murmu takes up role of teacher for school students, stresses environment conservation
Arunachal Pradesh government to close down zero enrolment schools: Education minister
Economic Survey Highlights: India is spending just 2.7% of GDP on education
Rain wreaks havoc in Nilgiris district, schools closed
Back to top