NCERT Class 12 Physics Chapter 3 Notes, Current Electricity Class 12 Chapter 3 Notes

NCERT Class 12 Physics Chapter 3 Notes: Download PDF

NCERT Class 12 Physics Chapter 3 Notes are a concise and clear summary of the Current Electricity chapter, which includes important definitions, key concepts, formulas, solved examples, and diagrams to make revision easier. Students are able to download the PDF version for easy study, last-minute preparation, and perform better in both Board and Competitive exams like JEE & NEET.

Download PDF

NCERT Class 12 Physics Chapter 3 Notes

NCERT Class 12 Physics Chapter 3 Notes discuss the chapter in a simple and organised way. NCERT Class 12 Physics Chapter 3 Notes include many key concepts like Ohm’s Law, resistivity, Kirchhoff’s laws, electrical circuits, etc, in order to understand these topics in a simple way. These notes are meant to facilitate faster revision by students and enhance problem-solving skills for examinations.

Electric Current:

• The flow of charge through a conductor per unit of time is defined as electric current. It is measured in amperes (A) and is essential for understanding electrical circuits and electromagnetism.

$
I=\frac{q}{t}
$

Where i is the current, q is the charge, and t is the time.

• If the rate of flow of charge is variable, the current at any time is i=dqdt
• Current Density: The amount of electric current flowing through a material per unit cross-sectional area is referred to as its current density. It is a vector quantity denoted by J and can be written as,

$\bar{j}=\frac{\Delta i}{\Delta A}$

• If the cross-sectional area is not perpendicular to the current but forms an angle θ with the current direction, then

$
\begin{aligned}
J_{a v} & =\frac{d i}{d A \cos \theta} \\
d i & =J d A \cos \theta=\vec{J} \cdot d \vec{A}
\end{aligned}
$

• Relation between current density and electric field

$\vec{J}=\sigma \vec{E}$

$\vec{J}=\frac{\vec{E}}{\rho}$

Where σ is the conductivity and ρ is the resistivity or specific resistance of the substance

• Mobility: Mobility for electrons is defined as the drift velocity per unit electric field.

$
\mu=\frac{v_d}{E}
$

Where μ is mobility and v_d is drift velocity

Ohm’s Law:

• Ohm's Law states that in a conductor, under constant external conditions such as temperature and pressure, the current flowing through the conductor is directly proportional to the potential difference across its two ends.

$
\begin{gathered}
V \propto I \\
V=I R
\end{gathered}
$

R- Electric Resistance

$
R=\rho \frac{l}{A}
$

where ρ is resistivity / specific resistance, l is the length of the conductor, and A is the area of the cross-section of the conductor

• Ohmic Substance: An Ohmic substance is a substance that obeys Ohm's Law. It has a linear I-V graph, and the slope gives the conductance, which is the reciprocal of resistance.
• Non-ohmic Substances: Non-ohmic or non-linear conductors are substances that do not obey Ohm's Law, such as gases and crystal rectifiers.
• Superconductor: Superconductors are materials that have zero resistivity below a critical temperature. Electrical resistance is zero in this state
• In a superconductor, resistivity is zero

,

Resistivity:

$\rho=\frac{m}{n e^2 \tau}$

Where m is the mass, n is the number of electrons per unit volume, e is the charge of the electron, and τ is the relaxation time.

• Resistivity is a material's intrinsic property, and its value tends to increase with the presence of impurities and mechanical stress.
• The reciprocal of resistivity is called conductivity.
• The reciprocal of resistance is termed conductance, and its SI unit is either Ω^-1 or Siemens.

Temperature-Dependent Resistivity:

ρ=ρ_o(1+α(T−T_o))

ρ: Resistivity at temperature T

ρ_o: Resistivity at temperature T_o

• Temperature Coefficient of Resistance

$
R_T=R_{0}\left[1+\alpha\left[T-T_0\right]\right]
$

$R_T$ - Resistance at temperature $T$
$R_0$ - Resistance at temperature $T_o$
$\alpha$ - temperature coefficient of resistance

$
\alpha=\frac{R_T-R_o}{R_o\left(T-T_o\right)}
$

Where the value of $\alpha$ is different at different temperatures

Colour Coding of Resistance:

The carbon resistance typically consists of four coloured ring bands labelled as A, B, C, and D.

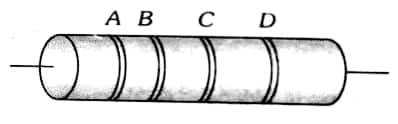
• Colour bands A and B indicate the significant digits of the resistance value.
• Colour band C represents the decimal multiplier.
• Colour band D indicates the tolerance, expressed as a percentage, around the specified resistance value.
• May be remembered as BBROY Great Britain Very Good Wife.

Tolerance of Gold is ±5%
Tolerance of Silver is ±10%
Tolerance if no colour ±20%

Grouping of Resistance:

Series Grouping of Resistance

$
R_{e q}=R_1+R_2+R_3+\cdots+R_n
$

$R_{e q}{ } = {\text {Equivalent Resistance }}$
For n-identical resistance: $R_{e q}=n R$

$
V^{\prime}=\frac{V}{n}
$

Parallel Grouping of Resistance:

$
\frac{1}{R_{e q}}=\frac{1}{R_1}+\frac{1}{R_2}+\cdots+\frac{1}{R_n}
$

If two resistances are in Parallel:

$
R_{e q}=\frac{R_1 R_2}{R_1+R_2}
$

Heat developed in a resistor:

• Heat developed in a resistor: When a steady current flows through a resistance R for time $t$, the loss in electric potential energy appears as increased thermal energy(Heat H) of the resistor and $H=i^2 R t$

• The power developed $=\frac{\text { energy }}{\text { time }}=i^2 R=i R=\frac{V^2}{R} \quad$ (from Ohm's law)

• Unit of heat is the joule (J)

• Unit of power is Watt (W)

Cell:

• The device which converts Chemical energy into electrical energy is known as an electric cell.
• Internal resistance: In the case of a cell, the opposition of the electrolyte to the flow of current through it. It is shown by r.
• The internal resistance of a cell depends on the distance between electrodes.

r∝d

• The internal resistance of a cell depends on the area of the electrodes

r∝A

• The internal resistance of a cell concentration of electrolyte

r∝c

• The internal resistance of a cell temperature of the electrolyte

r∝1/temp

• Emf of a cell: The electromotive force (emf) of a cell is defined as the work done or energy carried by a unit charge when it completes one full cycle within the circuit.
• Potential difference: The potential difference, also known as voltage, is the electrical pressure across the terminals of a cell when it is actively supplying current to an external resistance in the circuit.
• Equation of cell:

1. When supplying the current: E=V+iR
2. When the cell is being charged: E=V−iR

• Current supplied by the cell:

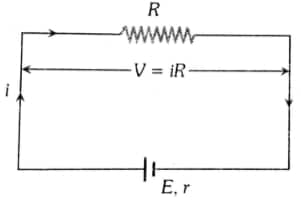
The cell supplies a constant current in the circuit.

$
i=\frac{E}{R+r}
$

Where R is the external resistance and r is the internal resistance

• Potential drop inside the cell=ir
• The internal resistance of the cell, $ r=\left(\frac{E}{V}-1\right) R $
• The power dissipated in external resistance, $ P=\left(\frac{E}{R+r}\right)^2 R $
• Maximum power is obtained when the resistance value of the load is equal in value to that of the voltage source's internal resistance.

$
P_{\max }=\frac{E^2}{4 r}
$

• Series grouping of cells:

In series grouping anode of one cell is connected to the cathode of the other cells

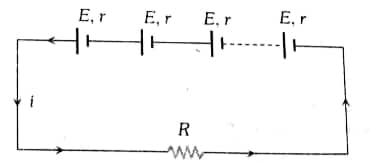
$n=$ identical cells which are connected in series, then
- Equivalent e.m.f of combination is $E_{e q}=n E$
- Equivalent internal resistance $r_{e q}=n r$
- Main current / current from each cell $i=\frac{n E}{R+n r}$
- Power dissipated in the external circuit is $\left(\frac{n E}{R+n r}\right)^2 \cdot R$
- Conditions for Maximum Power are $R=n r$
- $P_{\text {max }}=n\left(\frac{E^2}{4 r}\right)$ when $n r<R$

• Parallel grouping of cells:

In parallel grouping, all anodes are connected to one point, and all cathodes are connected together at other points

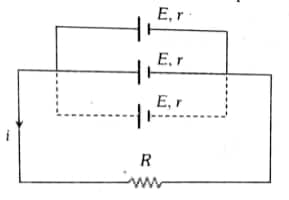
For n cells connected in parallel
Equivalent e.m.f $E_{e q}=E$
Equivalent internal resistance $R_{e q}=\frac{r}{n}$
The main current is

$
i=\frac{E}{R+\frac{r}{n}}
$
The potential difference across the external resistance

$
V=i R
$
Current from each cell

$
i^{\prime}=\frac{i}{n}
$

The power dissipated in the circuit

$
P=\left(\frac{E}{R+\frac{r}{n}}\right)^2 \cdot R
$

Condition for Maximum Power

$\begin{aligned} & R=\frac{r}{n} \\ & P_{\max }=n\left(\frac{E^2}{4 r}\right) {\text {when } r>>n R}\end{aligned}$

Kirchhoff's first law:

• In a circuit, at any junction, the sum of the currents entering the junction must equal the sum of the currents leaving the junction. This law is also known as the Junction rule or Kirchhoff's current law (KCL)

∑i=0

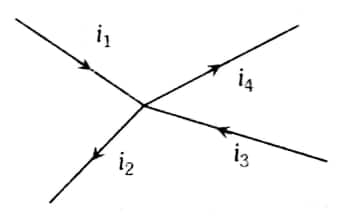
i₁+i₃=i₂+i₄

This law is simply based on the conservation of charge.

Kirchhoff's second law:

• The algebraic sum of all the potentials across a closed loop is zero. This law is also known as Kirchhoff's Voltage Law (KVL)
• This law is based on the conservation of energy.

∑V=0

In closed-loop

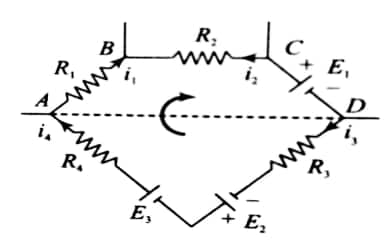
$-i_1 R_1+i_2 R_2-E_1-i_3 R_3+E_2+E_3-i_4 R_4=0$

Wheatstone's Bridge:

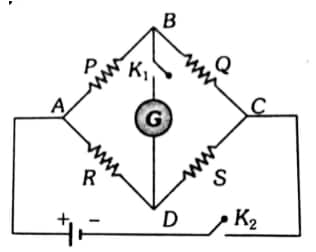
It is an arrangement of four resistances that can be used to measure one of them in terms of rest

$
\begin{aligned}
& \frac{P}{Q}=\frac{R}{S} \\
& V_B=V_D
\end{aligned}
$

(Balanced condition)
No current will flow through the galvanometer
unbalanced condition: $V_B>V_D$

$
\left(V_A-V_B\right)<\left(V_A-V_D\right)
$

Current will flow from $A$ to $B$

Meter bridge:

• The meter bridge is used to find the resistance of a wire, enabling the calculation of its specific resistance. Operating on Wheatstone's bridge principle, it provides a precise method for measuring resistance by balancing known and unknown resistances.

$\frac{P}{Q}=\frac{R}{S} \Rightarrow S=\frac{(100-l)}{l} R$

Current Electricity Class 12 Physics: Previous Year Question and Answer

One of the best ideas to reinforce your Class 12 Physics Chapter 3: Current Electricity is through preparation using questions from the previous year. These PYQs will assist you in recognising critical points, learning the exam format and gaining better accuracy in solving the problem. Through these questions, students will be able to develop confidence in CBSE board exams and any other competitive exams, such as JEE and NEET. These are some of the past-year questions that have answers elaborated, which guarantees this strong revision and improves your overall performance in the exam.

Q1: n identical cells, each of e.m.f. E and internal resistance r are connected in series. Later on, it was found out that the two cells ' X ' and ' Y ' are connected in reverse polarity. Calculate the potential difference across the cell ' X '.

Answer:

Two cells are connected in reverse polarity
So total emf $=(n-2) E-2 E$

$
\begin{aligned}
& =(n-2-2) E \\
& =(n-4) E
\end{aligned}
$

$
\begin{aligned}
& \text { Req }=n r \\
& I=\frac{E_{n e t}}{R_{e q}}=\frac{(n-4) E}{nr}
\end{aligned}
$

potential difference across cell $X=E+I r$

$
\begin{aligned}
& = E+ \frac{(n-4) E}{n r} \times r \\
& =\frac{nE+(n-4) E}{n} \\
& =\frac{n E+(n-4) E}{n} \\
& =\frac{E(n+n+4)}{n}=\frac{2 E(n+2)}{n}
\end{aligned}
$

Q2: Two batteries of emf's 3 V and 6 V and internal resistances 0.2Ω and 0.4Ω are connected in parallel. This combination is connected to a 4Ω resistor. Find the equivalent internal resistance of the combination

Answer:

Given:
Two batteries are connected in parallel, and then connected to an external resistor of $ R=4\Omega$.
Battery $1: {E}_1=3 \mathrm{~V}, r_1=0.2 \Omega$
Battery $2: {E}_2=6 \mathrm{~V}, r_2=0.4 \Omega$

The equivalent internal resistance of the combination is calculated using the formula:

$
r_{e q}=\frac{r_1 \cdot r_2}{r_1+r_2}
$

Substitute the values into the formula:

$
r_{e q}=\frac{0.2 \cdot 0.4}{0.2+0.4}=\frac{0.08}{0.6}=\frac{2}{15} \Omega \approx 0.133 \Omega
$

Hence, the equivalent internal resistance of the combination is 0.133 ohms.

Q3: Two wires P and Q are made of the same material. The wire Q has twice the diameter and half the length as that of wire P. If the resistance of wire P is R, the resistance of wire Q will be:

Answer:

$
\begin{gathered}
R=\frac{\rho l}{A}=\frac{\rho l}{\pi r^2} \\
\text { Resistance of } Q=R \text { ' }=\frac{\rho\left(\frac{l}{2}\right)}{\pi(2 r)^2} \\
R^{\prime}=\frac{\rho l}{\pi r^2 \cdot 4 \times 2}=\frac{\rho l}{8 \cdot \pi r_2}=\frac{R}{8}
\end{gathered}
$

Importance of NCERT Notes Class 12 Physics Chapter 3 Current Electricity

Understanding Class 12 Physics Chapter 3: Current Electricity becomes much easier when students use well-structured NCERT notes that simplify every concept. These notes break down laws, formulas, circuit concepts, and numerical methods in a clear and systematic way. They help build strong conceptual clarity, which is essential for both board exams and competitive exams like JEE and NEET.

Foundation of Electronics

• The concepts of current, resistance, and circuits are the basis of electronics that are required to become useful in the 21st century. This makes it an academically relevant chapter and is applicable to real-life situations.

Key for Competitive Exams

• Questions based on the same principles of Ohm's law, Kirchhoff's rules and circuit analysis are often included in JEE, NEET competitive exams - making these notes effectively useful for revision.

Easy to Revise

• Well-organised notes will compress theoretical material into short and easy points so students can revise it in a shorter time and also understand it if revision is needed close to the exam.

Better Numerical Problem Solving

• Notes will contain formulas, worked examples, and shortcuts for students to consult and reference to solve numerical questions quickly and accurately.

Learning Aid

• Notes will contain a labelled diagram of circuits, Wheatstone bridge and meter bridges, so that it is easier to visualise in addition to recall in an exam context.

Directly Relevant to the Board Exam

• Many questions asked by the CBSE Class 12 board exams are also directly from this chapter; therefore, the notes have scoring potential from the notes.

How to Master Class 12 Physics Chapter 3: Current Electricity?

Learning Class 12 Physics Chapter 3 Current Electricity is significantly simpler when you take a logical, systematic approach towards it. It is a scoring and conceptual chapter, and is considered important in both CBSE Board exams and competitive exams such as JEE and NEET. It is easy to develop excellent conceptual clarity and be able to work out theoretical and numerical questions of this chapter with the right study plan, regular revision, and appropriate practice.

• Begin with a proper reading of the NCERT textbook, knowing the fundamental points such as current, drift velocity, resistance and resistivity and then proceed to the complicated aspects.
• Write very brief notes of formulas like Ohm's Law, conductivity, internal resistance and rules of Kirchhoff to make revision easier and memorise several important relations in a very short time.
• Solve numerical problems every day using NCERT, exemplar, and past year papers in order to develop accuracy, particularly where it concerns Wheatstone bridge, meter bridge and series-parallel circuit.
• Draw circuit diagrams in a clean way, learn to label components appropriately, as most questions in the board exams require well-illustrated diagrams and a logical circuit analysis.
• To enhance your confidence level in applying the rules of the loop and junction when solving problems related to Kirchhoff, solve as many questions as possible in the many Kirchhoff Law questions, which are very common in competitive exams.
• Use NCERT diagrams and derivations to strengthen theory-based answers and ensure you can write stepwise, well-structured solutions for board exam questions.
• Definitions, units and SI values should be revised periodically, as a large number of short-answer questions are asked directly based on these fundamentals.
• Practice on time-timed mock tests and sample papers to make sure that they can work faster, as well as know their weak points and the actual pattern.

NCERT Class 12 Notes Chapterwise

NCERT Class 12 Notes chapterwise provide a structured way for students to revise all Physics concepts with clarity and ease. These notes cover every chapter in a concise format, including key definitions, formulas, diagrams, and solved examples. With chapterwise PDF links, students can access them quickly for board exam prep and competitive exams like JEE and NEET.

Subject Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 12 Solutions
• NCERT Exemplar Class 12 Maths
• NCERT Exemplar Class 12 Physics
• NCERT Exemplar Class 12 Chemistry
• NCERT Exemplar Class 12 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 12 Mathematics
• NCERT Solutions for Class 12 Chemistry
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus