Atoms Class 12th Notes - Free NCERT Class 12 Physics Chapter 12 Notes - Download PDF

NCERT Class 12 Physics Chapter 12 Notes: Download PDF

Download the NCERT Class 12 Physics Chapter 12 Notes Atoms PDF free of cost and have a quick revision of the class 12 physics chapter in a simplified manner. These notes deal with Rutherford’s Model, Bohr’s Theory, Atomic Spectra, and De Broglie Hypothesis with the help of easy explanations, diagrams, and important formulas. These are also very helpful to revise the whole syllabus quickly before CBSE board exams, JEE, and NEET.

Download PDF

NCERT Class 12 Physics Chapter 12 Notes

NCERT Class 12 Physics Chapter 12 Notes simplify the complicated concepts that atomic models, spectra, and quantum theory deal with, in very easy points to understand by students. The step-wise explanation of a concept, the provision of diagrams, and the use of formulae make these notes perfect for CBSE board exams as well as for other competitive exams like JEE and NEET.

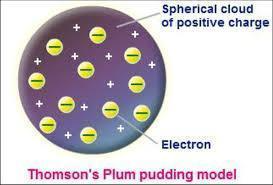
Thomson’s Atomic Model (Plum Pudding Model)

J. J. Thomson, who discovered the electron in 1897, proposed the plum pudding model of the atom in 1904 before the discovery of the atomic nucleus in order to include the electron in the atomic model. In Thomson’s model, the atom is composed of electrons surrounded by a soup of positive charge to balance the electrons’ negative charges, like negatively charged “plums” surrounded by positively charged “pudding”.

Drawbacks

• Failed to explain the results from the alpha-particle scattering experiment.
• Failed to explain atomic spectra.

Alpha Particle Scattering and Rutherford’s Nuclear Model of the Atom

Rutherford and his colleagues, Geiger and Marsden bombarded a thin gold foil of thickness approximately $8.6\times {10}^{-6}\mathrm{cm}$ with a beam of alpha particles in a vacuum. They used gold since it is highly malleable, producing sheets that can be only a few atoms thick, thereby ensuring the smooth passage of the alpha particles. A circular screen coated with zinc sulphide surrounded the foil. Since the positively charged alpha particles possess mass and move very fast, it was hypothesised that they would penetrate the thin gold foil and land on the screen, producing fluorescence in the part they struck.

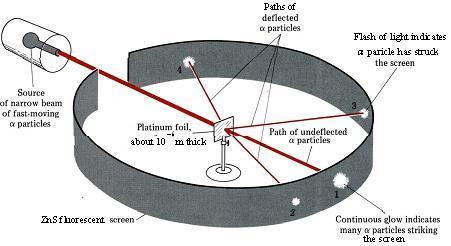
Observations:

• Most of the alpha particles behaved as expected, but there was a noticeable fraction of particles that got scattered by angles greater than 90 degrees.
• There were about 1 in every 2000 particles that got scattered by a full 180 degrees.
• The distribution of scattered α-particles was analysed and plotted as a graph as a function of scattering angle (θ).

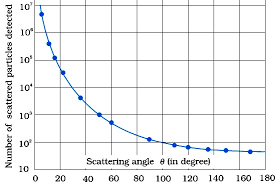
For a detector at a specific angle $(\theta )$ with respect to the incident beam, the number of particles per unit area striking the detector is given by the Rutherford formula:

$N(\theta )\propto \frac{1}{{\sin }^4\left(\frac{\theta }{2}\right)}$

Conclusion:

• Most of the atom is empty space, since most particles pass undeflected.

• The positive charge and mass of the atom are concentrated in a very small, dense region, which repelled the few alpha particles that were deflected. This region was named the nucleus.

• Electrons revolve around the nucleus in circular orbits at very high speeds, like planets orbiting the Sun.

• The atom remains electrically neutral as the positive charge of protons is balanced by the negative charge of electrons.

• The electrostatic force of attraction between electrons and protons provides the centripetal force needed to keep the electrons in their orbits.

Limitations:

• Could not explain the stability of the atom (electrons should spiral into the nucleus).

• Did not explain the discrete spectral lines of hydrogen.

• Could not describe atoms with more than one electron.

Alpha-particle Trajectory

We can understand the trajectory of alpha particles by calculating the distance of closest approach and the impact parameter.

Distance of Closest Approach

The distance of the closest approach in Rutherford scattering refers to the minimum distance between an incoming alpha particle and the nucleus of the target atom during a scattering event. At this distance, the entire initial kinetic energy has been converted into potential energy.

$\begin{array}{rl}(\text{K.E.}{)}_{\text{initial}}=\frac{1}{2}m{v}^2& =\frac{1}{4\pi {\epsilon }_0}\cdot \frac{(Ze)2e}{r_0}\\ ⟹r_0& =\frac{Z{e}^2}{m{v}^2\pi {\epsilon }_0}=\frac{4kZ{e}^2}{m{v}^2}=\frac{2kZ{e}^2}{K}\end{array}$

Impact Parameter

Impact parameter is defined as the perpendicular distance of the velocity of the alpha particle from the centre of the nucleus when it is far away from the atom. The shape of the trajectory of the scattered alpha particle depends on the impact parameter 'b' and the nature of the potential field. Rutherford deduced the following relationship between the impact parameter 'b' and the scattering angle $\theta$. It is given as

$\begin{array}{rl}b& =\frac{Z{e}^2\cot (\theta /2)}{4\pi {\epsilon }_0\left(\frac{1}{2}m{v}^2\right)}\\ \Rightarrow b& \propto \cot (\theta /2)\end{array}$

Electron Orbits

According to Rutherford, the electrostatic force of attraction provided the required centripetal force for orbit.

$\begin{array}{r}\therefore F_c=F_e\\ \frac{m{v}^2}{r}=\frac{1}{4\pi {\epsilon }_0}\frac{Z{e}^2}{r^2}\\ r=\frac{Z{e}^2}{4\pi {\epsilon }_{0}m{v}^2}\end{array}$

Here,
r=radius of orbit,
v = velocity of orbiting electron,
e = charge of an electron,
m = mass of an electron,
Z = atomic mass of the atom,
ε₀= permittivity of free space

Kinetic Energy(K):

$K=\frac{1}{2}m{v}^2=\frac{Z{e}^2}{8\pi {\epsilon }_{0}r}$

Potential Energy(U):

Using the electrostatic potential between 2 charged bodies, we get:

$U=\frac{1}{4\pi {\epsilon }_0}\frac{-eX+Ze}{r}=\frac{-Z{e}^2}{4\pi {\epsilon }_{0}r}$

Here, negative signs show that there is a force of attraction, and energy has to be given to the system to overcome this force of attraction.

Total Energy(T):

T = U + K

Some important relations to note:

Kinetic energy (K) = -(1/2)Potential energy(U)
Kinetic energy (K) = -Total energy(T)
Potential energy(U) = 2×Total energy(T)

Atomic Spectra

• When electrons in an atom absorb energy, they jump to higher energy levels (excited state).
• When they return to lower energy levels (ground state), they emit energy in the form of light.
• This emitted light, when passed through a prism, shows discrete lines known as the line spectrum or atomic spectrum.
• Each element has a unique atomic spectrum.
• These spectral lines correspond to specific wavelengths (energies) of emitted radiation.
• The atomic spectrum of hydrogen is divided into series based on the final energy level.

Bohr Model of the Hydrogen Atom

Proposed by Niels Bohr in 1913, this model explained the stability of the atom and the line spectra of hydrogen, improving upon Rutherford’s nuclear model. By combining classical and early quantum concepts, Bohr's Model of the hydrogen atom has three postulates.

(1) Atoms have certain definite stable states in which they can exist, and each possible state has a definite total energy. These are called the stationary states of the atom. In these states, electrons don't radiate energy.

For electrons revolving in a stable orbit, the necessary centripetal force is provided by the coulomb's force

$\frac{m{v}_n^2}{r_n}=\frac{kz{e}^2}{r_n^2}$

(2) This postulate states that the electron revolves around the nucleus only in those orbits for which the angular momentum is some integral multiple of $\frac{h}{2\pi }$ where h is Planck’s constant (= 6.6 × 10^–34 J s). Thus, the angular momentum (L) of the orbiting electron is quantised.

$L=m{v}_n{r}_n=\frac{nh}{2\pi };n=1,2,3\dots \dots \mathrm{\infty }$

(3). Bohr’s third postulate states that when an electron makes a transition from a higher to a lower energy orbit, it emits a photon with energy equal to the energy difference between the initial and final states. The frequency of the emitted photon is then given by $h\nu =E_i-E_f$

Using the first and second postulates, we can find the radius of the electron orbit.

$\begin{array}{r}{r}_n=\frac{n^2{h}^2}{4{\pi }^{2}kZm{e}^2}=\frac{n^2{h}^2{\epsilon }_0}{\pi mZ{e}^2}=0.53\frac{n^2}{Z}(k=\frac{1}{4\pi {\epsilon }_0})\\ \Rightarrow r_n\propto \frac{n^2}{Z}\end{array}$

We can find the energy of an electron in a stable orbit using Rutherford's expression for total energy.

$T=\frac{-Z{e}^2}{8\pi {\epsilon }_{0}r}$

By putting the value of Bohr’s radius, we get

$T=\frac{-m{e}^2}{8\pi {\epsilon }_0^2{n}^2{h}^2}$

By putting the values of electron mass (m), charge (e), the permittivity of free space (ε₀), and Planck’s constant (h), we get,

$T=\frac{-13.6}{n^2}eV$

Energy Levels

In Bohr's atomic model, the energy levels of an electron in an atom are quantised. This means that electrons can only occupy specific, discrete energy levels and cannot exist in between these levels. The potential energy is always negative, indicating that the electron is bound to the nucleus.

The energy of $n^{\text{th}}$ level of the hydrogen atom $(z=1)$ is given as :
$E_n=-\frac{z^{2}13.6}{n^2}\mathrm{eV}=-\frac{13.6}{n^2}\mathrm{eV}(\because z=1)$

• Energy of ground state $(n=1)$
  $E_1=-\frac{13.6}{1}\mathrm{eV}=-13.6\mathrm{eV}$
• Energy of first excited state $(n=2)$
  $E_2=-\frac{13.6}{4}\mathrm{eV}=-3.4\mathrm{eV}$
• Energy of the second excited state $(n=3)$
  $E_3=-\frac{13.6}{9}\mathrm{eV}=-1.51\mathrm{eV}$
• Energy of the third excited state $(n=4)$
  $E_4=-\frac{13.6}{16}\mathrm{eV}=-0.85\mathrm{eV}$

Line Spectra of Hydrogen Atom

According to Bohr, when an atom makes a transition from a higher energy level to a lower energy level, it emits a photon with energy equal to the energy difference between the initial and final levels. If E_i, is the initial energy of the atom before such a transition, E_f is its final energy after the transition, then conservation of energy gives the energy of the emitted photon.

$\begin{array}{r}\mathrm{h}v=\frac{\mathrm{hc}}{\lambda }=E_i-E_{\mathrm{f}}\\ \frac{hc}{\lambda }=\frac{-13.6}{n_i^2}\mathrm{eV}-\frac{-13.6}{n_f^2}\mathrm{eV}=13.6\mathrm{eV}(\frac{1}{n_f^2}-\frac{1}{n_i^2})\\ Rch=13.6\mathrm{eV}=1\text{Rydberg energy}\\ \Rightarrow \frac{1}{\lambda }=R(\frac{1}{n_f^2}-\frac{1}{n_i^2})\end{array}$
where $R=$ Rydberg's constant $=1.097\times {10}^7{\mathrm{m}}^{-1}$

The Line Spectra Of the Hydrogen Atom and its different series can be seen from the diagram below.

De-Broglie's Explanation of Bohr's Second Postulate

De-Broglie explanation of Bohr's Second Postulate show us clearly as to why the angular momentum of the revolving electron is the integral multiple of the $h/2\pi$. In his experiment he proved that the electron revolving in a circular orbit has a wave nature. Davison and Germer also proved that the electron shows the wave nature. In analogy to waves travelling on a string, particle waves too can lead to standing waves under resonant conditions. This occurs when the total distance travelled by a wave down the string and back is any integral number of wavelengths.

For an electron moving in $n^{\text{th}}$ circular orbit of radius $r_n$, the total distance is the circumference of the orbit, $2\pi r_n$.

$\therefore 2\pi r_n=n\lambda ,n=1,2,3\dots$

We also know, $\lambda =\frac{h}{p}=\frac{h}{m{v}_n}$

From the above equations, we have,

$2\pi r_n=\frac{nh}{m{v}_n}⟹m{v}_n{r}_n=\frac{nh}{2\pi }$

This is the quantum condition proposed by Bohr for the angular momentum of the electron. Thus, De-Broglie's hypothesis confirms Bohr’s second postulate for the quantisation of angular momentum of the orbiting electron.

Limitations of Bohr's Model

• The model works well only for hydrogen and other single-electron systems (like He⁺, Li²⁺). It fails for multi-electron atoms (like helium, lithium, etc.).

• Could not explain the fine structure or small splitting of spectral lines seen in high-resolution spectra.

• Failed to explain: Zeeman and Stark effect – splitting of spectral lines in a magnetic and electric fields.

Atoms: Previous Year Question and Answer

Q.1 Write the short comings of Rthe utherford atomic model. Explain how these were overcome by the postulates of Bohr’s atomic model.

Answer:

Rutherford’s Model

1. While the electrons are moving around the nucleus, they'll lose energy constantly. After losing energy, they should fall into the nucleus ultimately. Hence atom should collapse, but in reality, this does not happen.
2. He could not explain the spectrum of an atom.

Bohr’s Atomic Model postulates

(i) Explained the stability of the nucleus by postulating that the electron can orbit the nucleus in only those special orbits in which it does not radiate energy.
(ii) Explained the line spectrum by postulating that the electron emits photons of well-defined, unique energies when it undergoes a transition from one permitted orbit to another.

Q.2 Use the Bohr model of the hydrogen atom to calculate the speed of the electron in the first excited state.

Answer:

The speed of the electron

$V_n=\frac{1}{n}\frac{e^2}{4\pi {\epsilon }_0}\times \frac{2\pi }{h}$

First existed a state $n=2$

$\begin{array}{rl}{V}_n& =\frac{1}{2}\frac{e^2}{4\pi {\epsilon }_0}\times \frac{2\pi }{h}\\ =\frac{1}{4}\times \frac{{(1.6\times {10}^{-19})}^2}{8.85\times {10}^{-12}\times 6.6\times {10}^{-34}}\\ =0.01096\times {10}^8\\ =1.096\times {10}^6{\mathrm{ms}}^{-1}\end{array}$

Q.3 How is the stability of the hydrogen atom in the Bohr model explained by de Broglie's hypothesis?

Answer:

The quantised electron orbits and energy states are due to the wave nature of the electron, and only resonant standing waves can persist. Thus, the De Broglie hypothesis gives an explanation for Bohr’s second postulate.

According to de Broglie's hypothesis

$\begin{array}{rl}2\pi r& =n\lambda =\frac{nh}{p}=\frac{nh}{mv}\\ \Rightarrow mvr& =\frac{nh}{2\pi }\end{array}$

Importance of NCERT Class 12 Physics Chapter 12 Notes

Foundation of Modern Physics

• Knowledge of atomic structure is the basis of modern physics and quantum mechanics. It is very important for CBSE Class 12, JEE, NEET exam preparation.

Explains Atomic Spectra

• It is very helpful for students to understand emission and absorption spectra of elements, which is a very important part of practical experiments and competitive exams.

Basis for Bohr Model

• Through this students are given ideas about electron orbits, energy levels, and transitions, which eventually become the main concepts of atomic theory and quantum physics.

Supports Quantum Mechanics Concepts

• Just the de Broglie hypothesis and wave-particle duality can be understood by atomic models.

Important for Numerical Problem Solving

• Frequently used are key formulas related to atomic energy levels, radius, and spectra in CBSE numerical problems, JEE, and NEET questions.

Applicable in Real-life Technologies

• Atomic concepts explain the occurrence of lasers, neon lights, X-rays, and electron microscopes, thus providing a link between theory and practice.

Crucial for Advanced Studies

• Students possessing a deep understanding of atoms will be ready to take up physics, chemistry, and engineering at the higher level.

Enhances Conceptual Understanding

• Photoelectric effect and atomic transitions become easy to understand through simplification of complex phenomena, and thus, conceptual clarity gets enhanced.

NCERT Notes Class 12 Chapterwise

NCERT Class 12 Physics chapterwise notes are the thoughtfully designed materials that help in simplifying difficult concepts and give a clear idea of each topic. The notes include the whole Class 12 NCERT Physics syllabus with brief explanations, key formulas, diagrams, and stepwise solutions of examples. These are not only suitable for CBSE board exams but also for various competitive exams such as JEE and NEET, thus making revision more convenient and efficient.

Subject Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 12 Solutions
• NCERT Exemplar Class 12 Maths
• NCERT Exemplar Class 12 Physics
• NCERT Exemplar Class 12 Chemistry
• NCERT Exemplar Class 12 Biology

Subject Wise NCERT Solutions

• NCERT solutions for class 12 mathematics
• NCERT solutions for class 12 chemistry
• NCERT solutions for class 12 physics

• NCERT solutions for class 12 biology

NCERT Books and Syllabus