NCERT Class 12 Physics Chapter 1 Notes Electric Charges and Fields

NCERT Class 12 Physics Chapter 1 Notes: Download PDF

NCERT Notes Class 12 Physics Chapter 1 Electric Charges and Fields: Download PDF is a convenient and well-structured study material that can be learned and revised in a fast manner. These NCERT Notes Class 12 Physics Chapter 1 will be structured in an exam-oriented structure, and it will be easier to remember the key ideas, formulas and diagrams. The PDF format can be accessed easily at any time, and students can concentrate on revision of CBSE board exams, JEE, and NEET.

Download PDF

NCERT Class 12 Physics Chapter 1 Notes

The NCERT Notes Class 12 Physics Chapter 1 are important in the development of a firm base in the chapter of Class 12 physics; electrostatics. They assist the students to master the fundamentals in a very short time, review essential formulae and be ready to take the board and competitive exams.

Electric Charge:

• Charge of a material body or particle is the property (acquired or natural) due to which it produces and experiences electrical and magnetic effects. Some of the naturally occurring charged particles are electrons, protons, α-particles, etc.
• Charge is a derived physical quantity & is measured in coulombs in S.I. unit. In practice we use mC(10⁻³C),μC(10⁻⁶C),nC(10⁻⁹C) etc.
• C.G.S. unit of charge = electrostatic unit= esu
• 1 coulomb =3×10⁹esu of charge
• Dimensional formula of charge =[M^∘L^∘T¹I¹]
• Electric charge is a scalar quantity
• SI unit is the Coulomb, and it is represented by the symbol "C."
• Dimension-[AT].
• Like charges repel each other, and unlike charges attract each other

Point Charge:

• When the size of charged bodies is significantly smaller than the distance between them, their representation is simplified, and they are treated as point charges.

Conductors and Insulators:

• Conductors are materials that allow electric charges to move through them and thus facilitate the flow of electricity.
• Insulators, on the other hand, are materials that obstruct the passage of electricity, making it difficult for electric charges to pass through them.

Methods of charging:

• A body can be charged by means of (a) friction, (b) conduction, (c) induction,

(a) Charging by Friction: When a neutral body is rubbed against another neutral body, then some electrons are transferred from one body to the other. The body which can hold electrons tightly draws some electrons, and the body which can not hold electrons tightly loses some electrons. The body which draws electrons becomes negatively charged and the body which loses electrons becomes positively charged.

For example, suppose a glass rod is rubbed with a silk cloth. As the silk can hold electrons more tightly and a glass rod can hold electrons less tightly (due to their chemical properties), some electrons will leave the glass rod and get transferred to the silk. So, in the glass rod their will be a deficiency of electrons, therefore it will become positively charged. And in the silk, there will be some extra electrons, so it will become negatively charged

(b) Charging by induction: When a charged body comes into contact with an uncharged body, one side of the neutral body becomes oppositely charged while the other side remains unchanged.

For example, if a positively charged glass rod is brought close to a piece of paper, the paper is attracted. This occurs because the rod attracts electrons in the paper, causing the edge of the paper closest to the rod to become negatively charged, while the opposite end becomes positively charged due to an electron deficiency.

(c) Charging by conduction: When two conductors come into contact, the charges will be distributed evenly between them.

For example, when a negatively charged plastic rod comes into contact with a neutral pith ball, some electrons from the rod transfer to the pith ball, causing the pith ball to become negatively charged.

Properties of Charge:

1. Additivity: The total charge (Q) in a system containing multiple charges(q₁,q₂,q₃…………q_n) is the sum of individual charges: q₁+q₂+.....q_n.
2. Conservation of Charge: It is not possible to create or destroy a charge; it can only be transferred. When rubbing a glass rod with silk, for example, the charge is transferred rather than created.
3. Independence of Velocity: The velocity of a particle has no effect on its charge.
4. Quantisation: The charge on a body is quantised, meaning it is an integral multiple of the elementary charge (e), where e=1.6×10⁻¹⁹C is the charge of an electron. Therefore, the charge (q) on a body is q = ne, where n is an integer.

Coulomb's Law:

Coulomb's Law states that the force of attraction or repulsion between two charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. Mathematically, it is expressed as:

F∝q₁q₂/r²

F=kq₁q₂/r²

Where,

• F is the electrostatic force between the charges,
• k is Coulomb's constant
• q₁ and q₂ are the magnitudes of the charges
• r is the separation between the charges.

k=1/4πϵ₀

Where

ϵ₀=8.854×10⁻¹²C²/N−m², known as the absolute permittivity of air or free space

The vector form of Coulomb's Law:

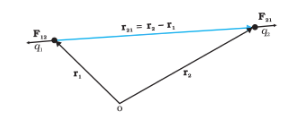
Consider two charges, q₁ and q₂, separated by r. Let the position vectors of q₁ be r_1, and that of q₂ be r₂. The force due to q₁ on q₂ is then directed along the unit vector r₁₂, as shown in the figure.

$\mathbf{F}_{21}=\frac{1}{4 \pi \varepsilon_o} \frac{q_1 q_2}{r_{21}^2} \hat{\mathbf{r}}_{21}$

$\mathbf{F}_{12}=\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r_{12}^2} \hat{\mathbf{r}}_{12}=-\mathbf{F}_{21}$

Force when a dielectric is inserted between the charges:

When the two charges are located in any medium, then the force between the two charges is,

$F_{m e d}=\frac{1}{4 \pi \epsilon} \frac{q_1 \times q_2}{r^2}$

$\frac{F_{\text {air }}}{F_{\text {med }}}=\frac{\frac{1}{4 \pi \epsilon_o} \frac{q_1 \times q_2}{r^2}}{\frac{1}{4 \pi \epsilon} \frac{q_1 \times q_2}{r^2}}=\frac{\epsilon}{\epsilon_o}$

$\begin{aligned} & \therefore \frac{F_{\text {air }}}{F_{\text {med }}}=k \\ & \Rightarrow F_{\text {med }}=\frac{F_{\text {air }}}{k}\end{aligned}$

The ratio ( $\epsilon / \epsilon_0$ ) of permittivity of the medium ( $\epsilon$ ) to the permittivity of free space ( $\epsilon_0$ ) is called relative permittivity $\left(\epsilon_{\mathrm{r}}\right)$ or dielectric constant $(\mathrm{k})$ of the given medium.

• The dielectric constant is the ratio of the permittivity of a substance to the permittivity of free space. (The dielectric will be explained later in detail in this chapter)

Principle of Superposition:

It states that the total force acting on a given charge as a result of a group of other charges is the vector sum of the individual forces acting on that charge as a result of each of the other charges.

Electrostatic Equilibrium:

The point where the resultant force on a charged particle becomes zero is called the equilibrium position.

• Stable Equilibrium: A charge is initially in equilibrium position and is displaced by a small distance. If the charge tries to return to the same equilibrium position, then this equilibrium is called a position of stable equilibrium.
• Unstable Equilibrium: If a charge is displaced by a small distance from its equilibrium position, and the charge has no tendency to return to the same equilibrium position. Instead, it goes away from the equilibrium position.
• Neutral Equilibrium: If the charge is displaced by a small distance and it is still in an equilibrium condition, then it is called neutral equilibrium.

Electric Field:

The region surrounding a charge, where another charged particle would experience a force, is referred to as the electric field in that space.

Electric Field Intensity:

The electric field intensity at any point is defined as the force experienced by a unit positive charge placed at that point.

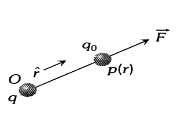
Electric field intensity,

$\mathbf{E}=\left(\frac{\mathbf{F}}{q_o}\right)$

where,

F is the force experienced by q_0,

• The SI unit of E is, Newton/Coulomb = Volt/meter = Joule/(Coulomb × Meter) and the dimensional formula is [MLT⁻³A⁻¹]
• The electric field is a vector quantity and due to the positive charge is away from the charge and for the negative charge, it is towards the charge.

Properties of electric field intensity $\vec{E}$:
(i) It is a vector quantity. Its direction is the same as the force experienced by a positive charge.
(ii) The direction of the electric field due to a positive charge is always away from it, while due to a negative charge, always towards it.
(iii) Its S.I. unit is Newton/Coulomb.
(iv) Its dimensional formula is [MLT⁻³ A⁻¹]

(v) Electric force on a charge q placed in a region of electric field at a point where the electric field intensity is $\vec{E}$ is given by $\vec{F}=q\vec{E}$. The electric force on a point charge is in the same direction of electric field on a positive charge and in the opposite direction on a negative charge.
(vi) It obeys the superposition principle, that is, the field intensity at a point due to a system of charges is the vector sum of the field intensities due to individual point charges.

i.e. $\mathbf{E}(\mathbf{r})=\mathbf{E}_1(\mathbf{r})+\mathbf{E}_2(\mathbf{r})+\ldots+\mathbf{E}_{\mathrm{n}}(\mathbf{r})$

(vii) It is produced by source charges. The electric field will be a fixed value at a point unless we change the distribution of source charges.

Electric Field Due To A Point Charge:

The electric field produced by a point charge q can be obtained in general terms from Coulomb's law. First, note that the magnitude of the force exerted by the charge q on a test charge q₀ is

$\mathbf{F}=\frac{1}{4 \pi \varepsilon_0} \frac{q q_o}{r^2} \hat{\mathbf{r}}$

Then divide this value by qo to obtain the magnitude of the field.

$\mathbf{E}(\mathbf{r})=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} \hat{\mathbf{r}}$

• If q is positive, E is directed away from q. On the other hand, if q is negative, then E is directed towards q.
• The electric field at a point is a vector quantity. Suppose E₁ is the field at a point due to a charge q₁ and E₂ is the field at the same point due to a charge q₂. The resultant field when both the charges are present is

E=E₁+E₂

• If the given charge distribution is continuous, we can use the technique of integration to find the resultant electric field at a point.

Electric field due to a system of charges:

The electric field obeys the superposition principle. That is the electric field due to a system of charge at a point is equal to the vector sum of all the electric fields.

Electric Lines of Force:

An electric field line is an abstract line or curve that is traced through a region of space so that its tangent at any point indicates the direction of the electric field at that point.

Properties of Electric Lines of Force (Electric Field Lines):

i) Electric forces diverge from positive charges and converge on negative charges.

ii) The number of field lines is proportional to the charge magnitude.

iii) Force lines never intersect because this would imply a contradiction in the direction of the electric field at the intersection point.

iv) Electric field lines do not form closed loops, as they cannot start and end on the same charge.

v) The direction of the force on a charged particle placed at any point on an electric field line is given by the tangent.

vi) Electric field lines do not represent a particle's actual path; they can only indicate the path if the electric field lines are straight.

vii) Electric field lines are normal to conductors if they originate or terminate on a conductor.

viii) Straight, parallel, and equidistant lines represent a uniform electric field.

ix) An electric field does not exist within a conductor.

Electric Flux ( ϕ ):

The Electric flux through an area is the number of electric field lines passing normally through that area.

• Flux through an area dA is given by

$dϕ=\vec{E}.\vec{dA}=EdAcos⁡θ$

here θ is the angle between the area vector and the electric field.

• Total flux through area A is

$ϕ=∫\vec{E}.\vec{dA}$

• Flux is a scalar quantity, and the SI unit of flux is volt-meter or weber (Wb).

Electric Dipole:

An electric dipole is made up of two equal and opposing charges separated by a small vector distance. The direction of the dipole moment is from the negative to the positive charge.

Electric Dipole Moment:

$\vec{p}=q\vec{2l}$

Here, 2l is the dipole length.

• The electric dipole moment($\vec{p}$) is a vector quantity from negative to positive charge, and its SI unit is Coulomb-meter (C·m).

Electric Field Due To An Electric Dipole At Axial and Equatorial Point:

i) At the axial point

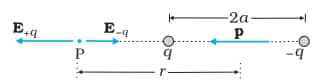
$\begin{aligned} \mathbf{E} & =\mathbf{E}_{+q}+\mathbf{E}_{-q}=\frac{q}{4 \pi \varepsilon_0}\left[\frac{1}{(r-a)^2}-\frac{1}{(r+a)^2}\right] \mathbf{p} \\ & =\frac{q}{4 \pi \varepsilon_o} \frac{4 a r}{\left(r^2-a^2\right)^2} \mathbf{p}\end{aligned}$

For $r \gg a$

$
\mathbf{E}=\frac{4 q a}{4 \pi \varepsilon_0 r^3} \hat{\mathbf{p}} \quad(r \gg a)
$

ii) At Equatorial Point

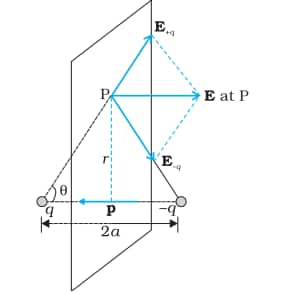
$\vec{E}=-\frac{2 q a}{4 \pi \varepsilon_o\left(r^2+a^2\right)^{3 / 2}} \mathbf{p}$

At large distances ( $r \gg a$ ), this reduces to

$
\mathbf{E}=-\frac{2 q a}{4 \pi \varepsilon_o r^3} \hat{\mathbf{p}} \quad(r \gg a)
$

Torque Experienced by the Dipole:

$\tau=\mathbf{p} \times \mathbf{E}$

$\begin{aligned} \text { Magnitude of torque } & =q E \times 2 a \sin \theta \\ & =2 q a E \sin \theta\end{aligned}$

Potential Energy of a Dipole

When an electric dipole is placed in an electric field E, a torque $\tau=\mathbf{p} \times \mathbf{E}$ acts on it. If we rotate the dipole through a small angle dθ, the work done by the torque is

dW=τdθdW=−pEsin⁡θdθ

The work is negative as the rotation dθ is opposite to the torque. The change in electric potential energy of the dipole is therefore

dU=−dW=pEsin⁡θdθ

Now, at angle θ=90^∘, the electric potential energy of the dipole may be assumed to be zero as net work done by the electric forces in bringing the dipole from infinity to this position will be zero.

Integrating,
From 90^∘ to θ, we have or

$U(\theta)=p E\left(\cos \frac{\pi}{2}-\cos \theta\right)=p E \cos \theta=-\mathbf{p} \cdot \mathbf{E}$

If the dipole is rotated from an angle θ₁ to θ₂, then

Work done by external forces =U(θ₂)−U(θ₁)

W_{ext forces} =−pEcos⁡θ₂−(−pEcos⁡θ₁)

W_{ext. forces} =pE(cos⁡θ₁−cos⁡θ₂)

or
and work done by electric forces,

Welectric force =−W_{ext. forces} =pE(cos⁡θ₂−cos⁡θ₁)

Continuous Charge Distribution:

A continuous charge distribution refers to the distribution of an amount of charge either uniformly or non-uniformly on a body. There are three main types of continuous charge distribution:

i) Linear charge distribution:

$\lambda=\frac{\Delta Q}{\Delta l}$

(λ)− charge per unit length.

Example: wire, circular ring

ii) Surface charge distribution:

$\sigma=\frac{\Delta Q}{\Delta S}$

(σ)− charge per unit Area

Example: plane sheet

iii) Volume Charge distribution

$\rho=\frac{\Delta Q}{\Delta V}$

(ρ)− charge per unit volume.

(charge on a dielectric sphere, etc)

Gauss's Law:

The total electric flux through a charged closed surface is equal to 1/ϵ₀ times the total charge q enclosed by the surface.

$\phi=\oint \vec{E} \cdot d \vec{s}=\frac{1}{\varepsilon_0} \sum_{i=1}^n q_i$

Notes:

• Gauss's law can be applied to any closed surface. The surface's size and shape do not matter.
• Gauss's law considers the electric field (E) as the result of all charges, whether inside or outside the Gaussian surface.
• The electric field outside the Gaussian surface has no effect on the net flux through it.
• The Gaussian surface is the surface chosen for the application of Gauss's law. Any Gaussian surface can be chosen, but be careful not to choose one that passes through any discrete charge. This is due to the fact that the electric field generated by a system of discrete charges is undefined at the location of any charge.
• Continuous charge distributions are allowed to pass through the Gaussian surface.
• Gauss's law is especially useful for simplifying the calculation of the electrostatic field in systems with some symmetry.

Applications of Gauss's Law:

1. Electric field due to an infinitely long straight uniformly charged wire:

The electric field produced by an infinitely long straight uniformly charged wire at a distance x from the wire must be determined.

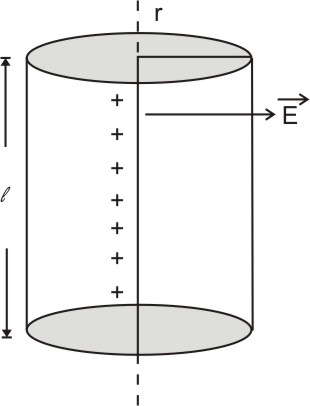
We have a cylindrical Gaussian surface of radius r=x and length l.
Charge enclosed by the surface

$\mathbf{E}=\frac{\lambda}{2 \pi \varepsilon_0 r} \hat{\mathbf{n}}$

2. Field due to a uniformly charged infinite plane sheet:

Let the plane sheet be positively charged

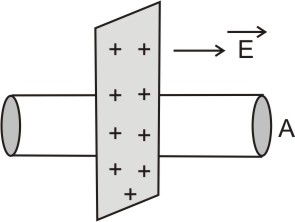
Let the Gaussian surface be a cylinder of cross-sectional area A

ϕ=E×2A

( the flux passes only through 2 circular cross-sections of the cylinder)

According to Gauss's law

ϕ=q/ε_o

E×2A=σA/ε_o

E=σ/2ε_o

3. Field due to a uniformly charged thin spherical shell

The radius of the shell is R, and the radius of the Gaussian surface (sphere) is r.

(i) Outside shell

$\mathbf{E}=\frac{q}{4 \pi \varepsilon_0 r^2} \hat{\mathbf{r}}$

(ii) Inside the shell

Since inside a spherical shell, charge =0, E=0

4. Electric field due to a point charge

The electric field due to a point charge is everywhere radial. We wish to find the electric field at a distance r from the charge q. We select Gaussian surface, a sphere at distance r from the charge. At every point of this sphere the electric field has the same magnitude E and it is perpendicular to the surface itself. Hence, we can apply the simplified form of Gauss's law,

ES=q_in/ε_o

Here, S= area of sphere =4πr² and

q_in = net charge enclosing the Gaussian surface =q

E(4πr²)=q/ε_o

$\vec{E}=\frac{q}{4 \pi \varepsilon_0 r^2}$

It is nothing but Coulomb's law.

Electric Field and Charges: Previous Year Question and Answer

Electric Charges and Electric Field: Previous Year Questions and Answers help students understand how electrostatics concepts are tested in actual exams. These questions highlight important topics, common problem patterns, and the level of conceptual clarity required. Practising previous year questions strengthens problem-solving skills, improves time management, and boosts confidence for board and competitive examinations.

Q1: Consider three metal spherical shells A, B and C, each of radius R. Each shell has a concentric metal ball of radius R/10. The spherical shells A, B and C are given charges +6q, -4q, and +14q, respectively. Their inner metal balls are also given charges −2q,+8q and 10q, respectively. Compare the magnitude of the electric fields due to shells A, B and C at a distance 3 R from their centres.

Answer:

The electric field at a distance $3 R$ from the centre of a spherical shell depends only on the net charge enclosed and is given by Gauss's law:

$
E=\frac{1}{4 \pi \epsilon_0} \frac{Q_{\text {net }}}{r^2}
$

where $Q_{\text {net }}$ is the total charge enclosed by each shell.
Net Charge on Each Shell -

For Shell A:

$
Q_A=6 q+(-2 q)=4 q
$

For Shell B:

$
Q_B=-4 q+8 q=4 q
$

For Shell C:

$
Q_C=14 q+(-10 q)=4 q
$
Since the total charge enclosed for all three shells is the same $(4 q)$, the magnitude of the electric field at a distance $3 R$ is identical for all:

$
E_A=E_B=E_C=\frac{1}{4 \pi \epsilon_0} \frac{4 q}{(3 R)^2}
$
Thus, the electric fields due to shells $\mathrm{A}, \mathrm{B}$, and C at a distance $3 R$ are equal.

Q2: A charge Q in fixed in position. Another charge q is brought near charge Q and released from rest. Which of the following graphs is the correct representation of the acceleration of the charge q as a function of its distance r from charge Q?

A.

B.

C.

D.

Answer:

We use Coulomb's Law and Newton's Second Law to determine the acceleration of charge q.
- The force on $q$ due to $Q$ is

$
F=\frac{k Q q}{r^2}
$

Acceleration is given by:

$
a=\frac{k Q q}{m r^2}
$
This means that acceleration varies inversely with $r^2$. The correct graph should show a decreasing function of r with a sharp drop.

Q3: State Gauss's law on electrostatics and derive an expression for the electric field due to a long straight thin uniformly charged wire (linear charge density λ ) at a point lying at a distance r from the wire.

Answer:

Gauss' Law states that the net electric flux through any closed surface is equal to $\frac{1}{\varepsilon_0}$ times the net electric charge within that closed surface.

$
\oint \overrightarrow{\mathrm{E}} . d \overrightarrow{\mathrm{~s}}=\frac{q_{\text {enclosed }}}{\varepsilon_o}
$

Electric field due to an infinitely long straight charged wire

In the diagram, we have taken a cylindrical Gaussian surface of radius $=\mathrm{r}$ and length $=l$.
The net charge enclosed inside the gaussian surface $q_{\text {enclosed }}=\lambda l$
By symmetry, we can say that the Electric field will be in a radially outward direction.
According to gauss' law,

$
\begin{aligned}
& \oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{~s}}=\frac{q_{\text {enclosed }}}{\varepsilon_o} \\
& \int_1 \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{~s}}+\int_2 \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{~s}}+\int_3 \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{~s}}=\frac{\lambda l}{\varepsilon_o} \\
& \int_1 \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{~s}} \& \int_3 \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{~s}} \text { are zero, since } \overrightarrow{\mathrm{E}} \text { is perpendicular to } d \overrightarrow{\mathrm{~s}} \\
& \int_2 \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{~s}}=\frac{\lambda l}{\varepsilon_o}
\end{aligned}
$

at $2, \overrightarrow{\mathrm{E}}$ and $d \overrightarrow{\mathrm{~s}}$ are in the same direction, we can write

$
\begin{aligned}
& E .2 \pi r l=\frac{\lambda l}{\varepsilon_o} \\
& E=\frac{\lambda}{2 \pi \varepsilon_o r}
\end{aligned}
$

Importance of Chapter 1: Electric Charges and Fields Notes

The Electric Charges and Fields Class 12 NCERT Notes are essential for building a strong conceptual base in electrostatics. They help students revise key laws, formulas, and diagrams efficiently, making exam preparation more effective for both board and competitive exams.

1. Electrostatics Foundation

• This chapter presents the science of charges at rest, which is electrostatics.

• The basic concepts in the construction of subsequent chapters, such as Electrostatic Potential, Capacitance, and Current Electricity, include charge, Coulomb's Law, electric field, electric field lines, and the superposition principle.

2. Clarity of Core Concepts

• Complex definitions like quantisation of charge, continuous charge distribution, and electric dipole are made simple through notes.
• The charts and briefings will assist students in having visual representations of abstract concepts such as field lines and their characteristics.

3. Quick Revision Tool

• Notes contain important derivations, key formulas and definitions all in a single place.

• Students would be able to reread the entire chapter within a limited time period before exams.

4. Boost to Competitive Exams (JEE/NEET)

• In JEE Mains/Advanced and NEET, electrostatics carries a high weightage.

• Significant formulas (such as the force between charges, field due to point charges, the moment of a dipole, and so on) and common problem-solving strategies are highlighted with notes.

5. Diagrammatic representation

• Charge distributions, field lines, and the direction of forces are commonly difficult to visualise.

• Notes have well-labelled diagrams that enhance comprehension and aid in scoring marks on exams.

6. Step-by-Step Problem Solving

• Notes comprised of previous year question examples that train students to apply concepts.

• They develop the analytical thinking skills that will be needed in numerical questions in CBSE and in the entrance exams.

How to Use NCERT Class 12 Physics Chapter 1 Notes Effectively?

The practical use of Electric Charges and Fields Class 12 NCERT Notes would greatly help in enhancing your knowledge on electrostatics and improve your exam performance. These notes will be able to make difficult concepts less complex, which will help in revision, but will be more focused. Through the appropriate study strategy, they may enable you to build the basics and resolve problems with confidence in board and competitive exams.

• The first step is to read the notes with the NCERT textbook to have a clear picture of the definitions, laws and the most fundamental concepts.

• Learn valuable formulas and derivations, and exercise using them on numerical problems on a regular basis.

• The notes include diagrams and illustrations of electric field lines, which are better to use in understanding concepts.

• Keep important points in mind by revising notes regularly to reduce stress in the last-minute exams.

• Revise the notes by solving NCERT questions, exemplar problems and questions of the previous year to test your level of understanding.

• Highlight key points in the notes that one can refer to when revising before exams.

Electric charges and fields Class 12 Notes: Chapterwise

NCERT Class 12 Physics Chapter 1 Notes Electric charges and fields give a clear and structured explanation of electrostatics, from the basics of charge to advanced applications like electric fields and Gauss’s law. These notes are organised chapterwise, making it simple for students to revise systematically and strengthen their preparation for board and competitive exams.

Subject Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 12 Solutions

• NCERT Exemplar Class 12 Maths

• NCERT Exemplar Class 12 Physics

• NCERT Exemplar Class 12 Chemistry

• NCERT Exemplar Class 12 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 12 Mathematics

• NCERT Solutions for Class 12 Chemistry

• NCERT Solutions for Class 12 Physics

• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus