NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields
Have you ever rubbed a balloon and seen your hair stand up, or have you seen dust particles on a TV screen? In these simple phenomena, we see the interesting action of electrical charges, small particles which either attract or push away each other. The NCERT Solutions Class 12 Physics Chapter 1 - Electric Charges and Fields provide the students with proper knowledge of the basic concepts, such as Coulomb Law, electric field intensity, electric dipole, electric flux and Gauss Law of the problem with step-by-step demonstrations.
For JEE Main 2026, qualifying scores vary by category: General – 95+ percentile (~180–200+ marks), OBC/EWS – 82+ percentile (~100–170 marks), SC/ST – 64.5+ percentile (~60–130+ marks). Top NITs/IITs require 99+ percentile (~240+ marks).
This Story also Contains
- NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields: Download PDF
- Electric Charges and Fields NCERT Solutions: Exercise Questions
- Electric Charges and Fields NCERT Solutions: Additional Questions
- Class 12 Physics Chapter 1 - Electric Charges and Fields: Topics And Subtopics
- Class 12 Physics Chapter 1 - Electric Charges and Fields: Important Formulas
- Approach to Solve the Questions of Class 12 Physics Chapter 1: Electric Charges and Fields
- How Can NCERT Solutions for Class 12 Physics Chapter 1 Help in Exam Preparation?
- Importance of NCERT Solutions for Class 12 Physics Chapter 1: Electric Charges and Fields
- What Extra Should Students Study Beyond NCERT for JEE/NEET?
- NCERT Solutions for Class 12 Physics: Chapter Wise

These NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields are prepared by subject matter experts according to the current CBSE Physics Class 12 syllabus of electrostatics, which simplifies complicated problems of electrostatics and enhances easy learning. Not only do they assist the students to score well in their board exams, but they also become a great resource in JEE, NEET and other competitive exams. These NCERT solutions enhance the clarity of concepts and enhance the speed of problem solving with elaborate derivations, solved examples and clear explanation of numericals. It is also possible to have the free PDF of NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields downloaded by the students and study offline, which will also be more convenient during revision. These Electric Charges and Fields class 12 question answers need to be practised regularly, so that one can understand them in more depth and is ready to take the exams and have a solid foundation to proceed with other topics in physics.
Also, Read -
NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields: Download PDF
The Class 12 Physics Chapter 1 - Electric Charges and Fields question answers are available in an easy-to-download PDF format for quick and effective revision. These class 12 physics chapter 1 Electric Charges and Fields question answers cover all the important concepts like Coulomb's Law, electric field, flux, and Gauss's Law, with clear, step-by-step explanations. Students can download the free PDF to access detailed answers anytime, making exam preparation and practice more convenient.
Electric Charges and Fields NCERT Solutions: Exercise Questions
The Electric Charges and Fields class 12 question answers offer a solution to each question in the exercises of the chapter and allow students to gain a robust knowledge of electrostatics. Important concepts such as Coulomb law, electric field, electric flux, and Gauss theorem are explained with the right words in these class 12 physics chapter 1 Electric Charges and Fields questions answers, hence preparing to undertake exams easily.
Answer:
Given,
$q_{1}$ = $2 \times 10^{-7}$ C
$q_{2}$ = $3 \times 10^{-7}C$
r = 30 cm = 0.3 m
We know,
The force between two charged particles, $q_{1}$ and $q_{2}$ separated by a distance r.
$F = \frac{1}{4\pi \epsilon _{0}} \frac{q_{1}q_{2}}{r^2}$
$ \Rightarrow F= \frac{1}{4\pi \epsilon _{0}} \frac{2\times10^{-7} \times 3 \times 10^{-7}}{(30\times10^{-2}\ m)^2\ }$
$\Rightarrow F= (9\times10^9\ N)\times \frac{6\times10^{-14+4}}{900\ m^2\ } = 6\times10^{-3} N$
Since the charges are of the same nature, the force is repulsive.
Answer:
Given,
$q_{1}$ = $0.4 \mu C$
$q_{2}$ = $-0.8 \mu C$
F = $-0.2N$ (Attractive)
We know,
The force between two charged particles, $q_{1}$ and $q_{2}$, separated by a distance r.
$F = \frac{1}{4\pi \epsilon _{0}} \frac{q_{1}q_{2}}{r^2}$
$\Rightarrow \\ -0.2 = 9\times10^9 \times \frac{(0.4\times10^{-6})(-0.8\times10^{-6})}{r^2} \\$
$\implies r^2 = 9\times10^9\times0.32\times10^{-12}/0.2 \\$
$\implies r^2 = 9\times0.16\times10^{-2} \\$
$\implies r = 1.2\times10^{-1} m = 0.12 m =12 cm$
Therefore, the distance between the two charged spheres is 12 cm.
Answer:
Using Newton's third law, the force exerted by the spheres on each other will be equal in magnitude.
Therefore, the force on the second sphere due to the first = 0.2 N
(This force will be attractive since charges are of opposite sign.)
Answer:
Electrostatic force
$F=\frac{KQ^2}{r^2}$
So the dimension of
$[Ke^2]=[Fr^2]$ ..................(1)
The gravitational force between two bodies of mass M and m is
$F=\frac{GMm}{r^2}$
So, the dimension of
$[Gm_em_p]=[Fr^2]$ .............(2)
Therefore, from (1) and (2)
$[\frac{ke^{2}}{Gm_{e}m_{p}} ]$ is dimensionless
Here,
K = $1/4\pi \epsilon _{0}$ , where $\epsilon _{0}$ is the permittivity of space.
$[1/ \epsilon _{0}] =[C/V.m] = [Nm^2 C^{-2}]$
e = Electric charge ([e] = [C])
G = Gravitational constant. ([G]= $[Nm^2kg^{-2}]$ )
$m_{e}$ and $m_{p}$ are mass of electron and proton ([ $m_{e}$ ] = [ $m_{p}$ ] = [Kg])
Substituting these units, we get
$[\frac{ke^{2}}{Gm_{e}m_{p}} ] = [\frac{C^2 \times Nm^2C^{-2}}{Nm^2kg^{-2}\times kg\times kg} ] = M^{0}L^{0}T^{0}$
Hence, this ratio is dimensionless.
Putting the value of the constants
$\frac{ke^{2}}{Gm_{e}m_{p}} = \frac{9\times10^9\times(1.6\times10^{-19})^{2}}{6.67\times10^{11}\times9.1\times10^{-31}\times1.67\times10^{-27}}=2.3 \times 10^{40}$
The given ratio is the ratio of the electric force $\frac{ke^{2}}{R^2}$ to the gravitational force between an electron and a proton $\frac{Gm_{e}m_{p}}{R^2}$, considering the distance between them is constant!
Q 1.4 (a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
Answer:
The given statement "electric charge of a body is quantised" implies that the charge on a body can take only integral values. In other words, only an integral number of electrons can be transferred from one body to another and not in fractions.
Therefore, a charged body can only have an integral multiple of the electric charge of an electron.
Answer:
On a macroscopic level, the amount of charge transferred is very large compared to the charge of a single electron. Therefore, we tend to ignore the quantisation of electric charge in these cases and consider it to be continuous in nature.
Answer:
When a glass rod is rubbed with a silk cloth, opposite charges appear on both the rod and the cloth.
The phenomenon of charging bodies by rubbing them against each other is known as charging by friction. Here, electrons are transferred from one body to another, giving both bodies an equal but opposite charge. The number of electrons lost by one body (attains a positive charge due to loss of negatively charged electrons) is equal to the number of electrons gained by the other body (attains a negative charge). Therefore, the net charge of the system is zero. This is in accordance with the law of conservation of charge
Answer:
Charges at (A, C) and (B, D) are pairwise diametrically opposite and also equal.
Therefore, their force on a point charge at the centre of the square will be equal but opposite in direction.
Now, AC = BD = $\sqrt{2}\times(10\times10^{-2} m) = \sqrt{2}\times0.1 m$
$\therefore$ AO = BO = CO = DO = r = Half of diagonal = $\sqrt{2}\times0.05 m$
Force on point charge at centre due to charges at A and C = $F_{A} = -F_{C} = \frac{k(2\mu C)(1\mu C)}{(r)^2}$
Similarly, force on point charge at centre due to charges at B and D = $F_{B} = -F_{D} = \frac{k(-5\mu C)(1\mu C)}{(r)^2}$
$\therefore$ Net force on point charge = $\\F_{A} + F_{B} + F_{C} + F_{D} = -F_{B} +F_{B} - F_{D} + F_{D} = 0$ .
Hence, the charge at the centre experiences no force.
Answer:
A positive point charge experiences a force in an electrostatic field. Since the charge will experience a continuous force and cannot jump from one point to another, the electric field lines must be continuous.
Q 1.7 (b) Explain why two field lines never cross each other at any point.
Answer:
A tangent drawn at any point on a field line gives the direction of force experienced by a unit positive charge due to the electric field at that point. If two lines intersect at a point, then the tangent drawn there will give two directions of force, which is not possible. Hence, two field lines cannot cross each other at any point.
Answer:
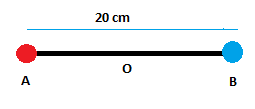
Given, AB = 20 cm
Since O is the midpoint of the line AB.
AO = OB = 10 cm = 0.1m
The electric field at a point caused by charge q is given as,
$E = \frac{kq}{r^2}$
Where q is the charge, r is the distance between the charges and the point O
k = 9x109 N m2 C -2
Now,
Due to the charge at A, the electric field at O will be $E_{A}$ and in the direction AO.
$E_{A} =\frac{ 9\times10^9 \times 3\times10^{-6}}{0.1^2}$
Similarly, the electric field at O due to the charge at B is also in the direction AO
$E_{B} =\frac{ 9\times10^9 \times (-3\times10^{-6})}{0.1^2}$
Since both the forces are acting in the same direction, we can add their magnitudes to get the net electric field at O:
E' = $E_{A}$ + $E_{B}$ = 2E (Since their magnitudes are same)
$E' =2\times \frac{ 9\times10^9 \times 3\times10^{-6}}{0.1^2} = 5.4\times 10^4 N/C$ along the direction AO.
Answer:
Let Q = $-1.5 \times10^{-9}$ C
The force experienced by Q when placed at O due to the charges at A and B will be:
$F = Q \times E$
where 'E' is the net electric field at point O.
$F=1.5 \times 10^{-9} C \times 5.4 \times 10^4 N/C = 8.1\times10^{-3 } N$
Q, being negatively charged, will be attracted by the positive charge at A and repelled by the negative charge at B. Hence, the direction of force experienced by it will be in the direction of OA.
Answer:
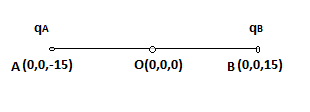
Given,
$q_{A}=2.5\times 10^{-7}C$ and $q_{B}=-2.5\times 10^{-7}$
The total charge of the system = $q_{A} + q_{B} = 0$
$\therefore$ The system is electrically neutral. (All dipole systems have net charge zero!)
Now, distance between the two charges, d = 15 + 15 = 30 cm = 0.3 m
We know, the electric dipole moment of the system, p = $q_{A}$ x d = $q_{B}$ x d (i.e, the magnitude of charge x distance between the two charges)
$\therefore p = 2.5\times10^{-7} C \times 0.3 m = 7.5\times10^{-8} Cm$
The direction of a dipole is towards the positive charge. Hence, in the positive z-direction.
Answer:
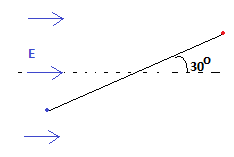
Given,
Electric dipole moment, p = $4\times 10^{-9} Cm$
$\theta = 30^{0} \ \therefore sin\theta = 0.5$
E = $5\times 10^{4}NC^{-1}$
We know that the torque acting on a dipole is given by:
$\tau = p \times E$
$\implies \tau = p Esin\theta = 4\times10^{-9} \times5\times10^{4}\times0.5 \ Nm$
$\implies \tau =10^{-4}Nm$
Therefore, the magnitude of torque acting on the dipole is $10^{-4}Nm$
Answer:
Clearly, polyethene being negatively charged implies that it has an excess of electrons(which are negatively charged!). Therefore, electrons were transferred from wool to polyethene.
Given, charge attained by polyethene = $-3\times 10^{-7}$ C
We know, Charge on 1 electron = $-1.6\times10^{-19} C$
Therefore, the number of electrons transferred to attain a charge of $-3\times 10^{-7} =\frac{-3\times 10^{-7}}{-1.6\times10^{-19} C} = 1.8\times10^{12}$ electrons.
Answer:
The charge attained by polyethene (and also wool!) is solely due to the transfer of free electrons.
We know, Mass of an electron = $9.1\times10^{-31}\ kg$
The total mass of electrons transferred = number of electrons transferred x mass of an electron
= $9.1\times10^{-31} \times 1.8\times10^{12}\ kg = 16.4\times10^{-19} \ kg$
Yes, there is a transfer of mass, but it is negligible.
Answer:
Since the radii of the spheres A and B are negligible compared to the distance of separation, we consider them as a point object.
Given,
charge on each of the spheres = $6.5\times 10^{-7}C$
and distance between them, r = 50 cm = 0.5 m
We know,
$F = k\frac{q_{1}q_{2}}{r^2}$
Therefore, the mutual force of electrostatic repulsion(since they have the same sign of charge)
$F = 9\times10^9Nm^{2}C^{-2}\times\frac{(6.5\times10^{-7}\ C)^2}{(0.5\ m )^2} = 1.5\times10^{-2} N$
Answer:
We know that the force between two charged particles separated by a distance r is:
$F = k\frac{q_{1}q_{2}}{r^2} = k\frac{q^2}{r^2}$ $(\because q_{1} = q_{2} = q)$
Now if $q\rightarrow 2q\ and\ r\rightarrow r/2$
The new value of force:
$F_{new} =k\frac{(2q)^2}{(r/2)^2} = 16k\frac{q^2}{r^2} = 16F$
Therefore, the force increases 16 times!
$F_{new} =16F = 16\times1.5\times10^{-2} N = 0.24\ N$
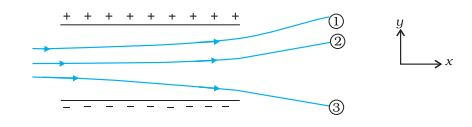
Answer:
Charges 1 and 2 are repelled by the negatively charged plate of the system
Hence, 1 and 2 are negatively charged.
Similarly, 3 being repelled by the positive plate is positively charged.
(charge to the mass ratio: charge per unit mass)
Since 3 is deflected the most, it has the highest charge-to-mass ratio.
Answer:
Given,
$E=3\times 10^{3}\ \widehat{i}\ \frac{N}{C}$
Area of the square = $0.01^2\ m^2$
Since the square is parallel to the yz plane, its normal is in the x-direction.(i.e $\widehat{i}$ direction )
Therefore, flux through this surface:
$\phi = E.A$
$\implies \phi = (3\times10^3\ \widehat{i}).(0.01\ \widehat{i}) Nm^2/C = \boldsymbol{30 Nm^2/C}$
Answer:
Now, since the normal of the square plane makes a $60^{\circ}$ angle with the x-axis
$cos\Theta = cos(60^{0}) = 0.5$
Therefore, flux through this surface:
$\phi = E.A = EAcos\theta$
$\implies \phi = (3\times10^3)(0.01)(0.5) Nm^2/C = \boldsymbol{15\ Nm^2/C}$
Answer:
The net flux of the uniform electric field through a cube oriented so that its faces are parallel to the coordinate planes is zero.
This is because the number of lines entering the cube is the same as the number of lines leaving the cube.
Alternatively,
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
Since there is no charge enclosed in the cube, $\phi = 0$.
Answer:
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
Given, $\phi = 8.0 \times10^3\ Nm^2/C$
$\therefore q = \phi \times\epsilon _{0} = (8.0\times10^3 \times8.85\times10^{-12})\ C$
$\implies q = 70 \times10^{-9} C = \boldsymbol{0.07 \mu C}$
This is the net charge inside the box.
Answer:
Using Gauss's law, we know that $\phi = q/\epsilon _{0}$
Since flux is zero, q = 0, but this q is the net charge enclosed by the surface.
Hence, we can conclusively say that the net charge is zero, but we cannot conclude that there are no charges inside the box.

Answer:
Let us assume that the charge is at the centre of the cube with an edge of 10 cm.
Using Gauss's law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
Therefore, flux through the cube: $\phi = (10\times10^{-6} C)/\epsilon _{0}$
Due to symmetry, we can conclude that the flux through each side of the cube, $\phi'$, will be equal.
$\therefore \phi' = \frac{\phi}{6} = \frac{10^{-5}}{6\times\epsilon _{0}} = \frac{10^{-5}}{6\times\ 8.85\times10^{-12}} = \boldsymbol{1.9 \times 10^5\ Nm^2C^{-1}}$
Answer:
Given,
q = net charge inside the cube = $2.0\mu C$
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
$\therefore \phi = 2.0\times10^{-6}/8.85\times10^{-12}\ Nm^2C^{-1} = \boldsymbol{2.2\times10^5\ Nm^2C^{-1}}$
(Note: Using Gauss's formula, we see that the electric flux through the cube is independent of the position of the charge and the dimension of the cube! )
Answer:
Given,
$\phi = -1.0\times 10^{3}\frac{Nm^{2}}{C}$
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
Therefore, flux does not depend on the radius of the sphere but only on the net charge enclosed. Hence, the flux remains the same although the radius is doubled.
$\phi' = -10^{3}\frac{Nm^{2}}{C}$
Answer:
Given,
$\phi = -1.0\times 10^{3}\frac{Nm^{2}}{C}$
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
$\therefore q = -10^{3}Nm^2C^{-1} \times 8.85\times10^{-12}N^{-1}m^{-2}C^{2} = -8.8\times10^{-9}\ C \\ = \boldsymbol{-8.8\ nC}$
Answer:
We know that, for determining the electric field at r>R for a conducting sphere, the sphere can be considered as a point charge located at its centre.
Also, the electric field intensity at a point P, located at a distance r, due to the net charge q is given by,
$E = k\frac{q}{r^2}$
Given, r = 20 cm = 0.2 m (From the centre, not from the surface!)
$\\ \therefore 1.5\times10^3 = 9\times10^9\times \frac{q}{0.2^2} \\ \implies q = \frac{1.5\times0.04}{9}\times10^{-6} = 6.67\times10^{-9}\ C$
Therefore, charge on the conducting sphere is $- 6.67\ nC$ (since flux is inwards)
Answer:
Given,
Surface charge density = $80.0\mu Cm^{-2}$
Diameter of sphere = 2.4 m $\therefore$ radius of sphere, r = 1.2 m
The charge on the sphere, Q = surface charge density x surface area of the sphere
$= (80\times10^{-6})\times(4\pi r^2) = 320\times22/7\times(1.2)^2 = \boldsymbol{1.45\times10^{-3}\ C}$
Answer:
Using Gauss's law, we know that :
$\phi = q/ \epsilon_{0}$
$\implies \phi = 1.45\times10^{-3}/ 8.85\times10^{-12} = 1.6\times10^{8}\ Nm^2C^{-1}$
Answer:
Given,
$\lambda = 9\times 10^{4}\frac{N}{C}$
d = 2 cm = 0.02 m
We know, for an infinite line charge having linear charge density $\lambda$, the electric field at a distance d is:
$E = k\lambda / d$
$\therefore 9\times10^4 = 9\times10^{9}\lambda / 0.02$
The linear charge density is $10 \mu C/cm$.
Answer:
We know the electric field, E, due to an infinite plate (length>>thickness) having surface charge density $\sigma$ = $\sigma/2\epsilon_{0}$.
(To note: It's independent of distance from the plate!)
In the region outside the first plate,
since both plates have the same surface charge density(in magnitude only), their electric fields are the same in magnitude in this region but opposite in direction.
(E due to positive plate away from it and E due to negative plate towards it!)
Hence, the electric field in the outer region of the first plate is zero.
Answer:
We know the electric field, E, due to an infinite plate (length>>thickness) having surface charge density $\sigma$ = $\sigma/2\epsilon_{0}$.
(To note: It's independent of distance from the plate and the same everywhere!)
In the region outside the second plate,
Since both plates have the same surface charge density(in magnitude only), their electric fields are the same in magnitude in this region but opposite in direction.
(E due to positive plate away from it and E due to negative plate towards it!)
Hence, the electric field in the outer region of the second plate is zero.
Answer:
We know the electric field, E, due to an infinite plate (length>>thickness) having surface charge density $\sigma$ = $\sigma/\epsilon_{0}$.
(To note: It's independent of distance from the plate!)
Let A and B be the two plates such that:
$\sigma_{A}= 17\times10^{-22} Cm^{-2}$ = $\sigma$
$\sigma_{B}= -17\times10^{-22} Cm^{-2}$ = - $\sigma$
Therefore,
The electric field between the plates, E = $E_{A} + E_{B}$ = $\sigma_{A}/2\epsilon_{0} + (-\sigma_{B}/2\epsilon_{0})$
$\Rightarrow E = \sigma/2\epsilon_{0} = 17\times10^{-22}/8.85\times10^{-12} = 1.92\times10^{-10 } NC^{-1}$
Electric Charges and Fields NCERT Solutions: Additional Questions
The NCERT Solutions for Class 12 Physics Chapter 1: Electric Charges and Fields include extra practice questions that help students strengthen their understanding of the chapter. These additional questions cover all important concepts like electric field, Coulomb’s law, and electric flux in an easy-to-understand way. Solving them regularly improves problem-solving skills and prepares students well for CBSE board exams and competitive tests like JEE and NEET.
Answer:
When two spheres of the same size are touched, on attaining the equipotential state, the total charge of the system is equally distributed on both of them.
Therefore, (i) When uncharged third sphere C is touched with A, charge left on A = $0.5\times 6.5\times 10^{-7}C$
and charge attained by C = $0.5\times 6.5\times 10^{-7}C$
(ii) Now, charge on B + charge on C = $6.5\times 10^{-7}C$ + $0.5\times 6.5\times 10^{-7}C$ = $1.5\times 6.5\times 10^{-7}C$
When touched, charge left on B = $0.5\times1.5\times 6.5\times 10^{-7}C$
Therefore $q_{A}\rightarrow 0.5\times q_{A}\ and\ q_{B}\rightarrow 0.75\times q_{B}$
Therefore,
$F' = 0.5\times0.75 \times F = 0.375 \times 1.5\times10^{-2} N = \boldsymbol{5.7\times10^{-3}\ N}$
Answer:
The force due to the electric field is balancing the weight of the oil droplet.
weight of the oil drop = density x volume of the droplet x g = $\rho \times \frac{4}{3}\pi r^3 \times g$
Force due to the electric field = E x q
charge on the droplet, q = No. of excess electrons x charge of an electron = $12\times q_{e} = 12\times 1.6\times10^{-19} = 1.92\times10^{-18} C$
Balancing forces:
$\rho \times \frac{4}{3}\pi r^3 \times g = E\times q$
Putting known and calculated values:
$\\ r^3 =\frac{3}{4\pi} E\times q / \rho\times g $
$ \Rightarrow r^3 = \frac{3}{4}\times\frac{7}{22}\times(2.55\times10^4)\times 1.92\times10^{-18} / (1.26\times10^3 \times10 ) $
$ \Rightarrow r^3 = 0.927\times10^{-18} m^3$
$r = 0.975\times10^{-6} m = 9.75\times10^{-4} mm$
Q 3. Which among the curves shown in Figure cannot possibly represent electrostatic field lines?

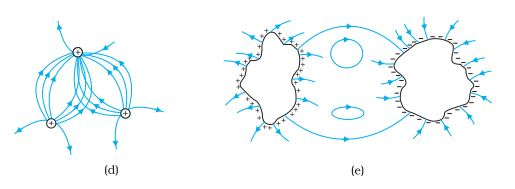
Answer:
(a) Wrong, because field lines must be normal to a conductor.
(b) Wrong, because field lines can only start from a positive charge. It cannot start from a negative charge,
(c) Right;
(d) Wrong, because field lines cannot intersect each other,
(e) Wrong, because electrostatic field lines cannot form closed loops.
Answer:
Force on a charge F=qE
But here E is varying along the Z direction.
Force can be written as,
$F=q\frac{dE}{dz}dz=P\frac{dE}{dz}=10^{-7}\times10^5=10^{-2}N$
Torque experienced =0 since both dipole and electric field are in the Z direction. The angle between the dipole and the electric field is 180 degrees
$\tau = \mathbf{p}\times \mathbf{E}=pE \sin 180=0$
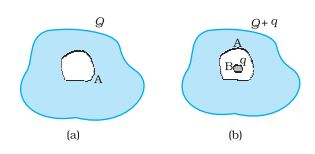
Answer:
We know that the electric field inside a conductor is zero.
Using Gauss's law, if we draw any imaginary closed surface inside the solid, the net charge must be zero. (Since E = 0 inside)
Hence, there cannot be any charge inside the conductor, and therefore, all charge must appear on the outer surface of the conductor.
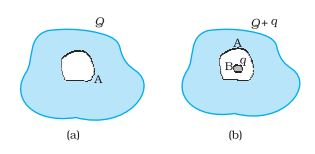
Answer:
We know that the electric field inside a conductor is zero.
Now, imagine a Gaussian surface just outside the cavity inside the conductor. Since E=0 (Using Gauss' law), the net charge must be zero inside the surface. Therefore, a -q charge is induced on the inner side of the cavity(facing conductor B).
Now consider a Gaussian surface just outside the conductor A. The net electric field must be due to charge Q and q. Hence, q charge is induced on the outer surface of conductor A. Therefore, the net charge on the outer surface of A is Q + q.
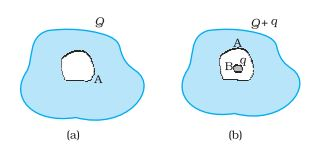
Answer:
We know that the electric field inside a conductor is zero.
Therefore, a possible way to shield from the strong electrostatic fields in its environment is to enclose the instrument fully by a metallic surface.
Answer:
Let the surface area of the sphere be S.
And assume that the hole is filled. For a point B, just above the hole, considering a Gaussian surface passing through B, we have
$\oint E.dS = q/\epsilon_{0}$
Now, since the electric field is always perpendicular to the surface of the conductor.
$\\ \therefore \oint E.dS = E.S= q/\epsilon_{0} = (\sigma.S)/\epsilon_{0} \\ \implies E = \sigma/\epsilon_{0}$
Using Superposition principle, $E =E_{1} + E_{2}$ ,
where $E_{1}$ is due to the hole and $E_{2}$ is due to the rest of the conductor. (both pointing outwards, i.e away from the centre)
Again, for a point A, just below the hole, the Electric field will be zero because of electrostatic shielding.
Using the superposition principle, this will be due to $E_{1}$ pointing inwards(towards the centre) and due to $E_{2}$ (Pointing away from the centre)
$0 =E_{1}-E_{2}$ $\implies E_{1}=E_{2}$
Using this relation, we get:
$E =E_{1} + E_{2} = 2E_{1} \implies E_{1} = E/2 = \sigma/2\epsilon_{0}$
Since this is pointing outwards,
$\boldsymbol{E_{1}} = \sigma/2\epsilon_{0}\ \boldsymbol{\widehat{n}}$ is the electric field in the hole.
(Trick:
1. Assume the hole to be filled.
2. Consider 2 points just above and below the hole.
3. Electric fields at these points will be due to the hole and the rest of the conductor. Use the superposition principle.)
[Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Answer:
Let AB be a long, thin wire of uniform linear charge density λ.
Let us consider the electric field intensity due to AB at point P at a distance h from it, as shown in the figure.
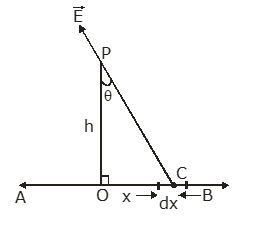
The charge on a small length dx on the line AB is q, which is given as q = λdx.
So, according to Coulomb’s law, the electric field at P due to this length dx is
$dE'=\frac{1}{4\pi \epsilon_o}\frac{\lambda dx}{(PC)^2}$
But $P C=\sqrt{h^2+x^2}$
$
\Rightarrow d E=\frac{1}{4 \pi \epsilon_o} \frac{\lambda d x}{\left(h^2+x^2\right)}
$
This electric field at P can be resolved into two components as dEcosθ and dEsinθ. When the entire length AB is considered, then the dEsinθ components add up to zero due to symmetry. Hence, there is only the dEcosθ component.
So, the net electric field at P due to dx is
dE' = dE cosθ
$
\Rightarrow d E^{\prime}=\frac{\lambda d x \cos \theta}{4 \pi \epsilon_o \left(h^2+x^2\right)}
$-----(1)
$\qquad$
$\ln \triangle \mathrm{POC}$
$
\tan \theta=\frac{x}{h}
$
$
\Rightarrow \mathrm{x}=\mathrm{h} \tan \theta
$
Differentiating both sides w.r.t. $\theta$,
$
\begin{aligned}
& \frac{d x}{d \theta}=h \sec ^2 \theta \\
& \Rightarrow \mathrm{dx}=\mathrm{h} \sec ^2 \theta \mathrm{~d} \theta .........(2)
\end{aligned}
$
Also, $h^2+x^2=h^2+h^2 \tan ^2 \theta$
$
\begin{aligned}
& \Rightarrow h^2+x^2=h^2\left(1+\tan ^2 \theta\right) \\
& \Rightarrow h^2+x^2=h^2 \sec ^2 \theta \ldots \ldots \ldots \ldots...........(3)
\end{aligned}
$
(Using the trigonometric identity, $1+\tan ^2 \theta=\sec ^2 \theta$ )
Using equations (2) and (3) in equation (1),
$
\begin{aligned}
& d E^{\prime}=\frac{\lambda \cos \theta \times h \sec ^2 \theta}{4 \pi \epsilon_o \times h^2 \sec ^2 \theta} d \theta \\
& d E^{\prime}=\frac{\lambda \cos \theta}{4 \pi \epsilon_o h} d \theta
\end{aligned}
$
The wire extends from $\theta=-\frac{\pi}{2}$ to $\theta=\frac{\pi}{2}$ since it is very long. Integrating both sides,
$
E^{\prime}=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\lambda \cos \theta}{4 \pi \epsilon_o h} d \theta
$
$\begin{aligned} & E^{\prime}=\frac{\lambda}{4 \pi \epsilon_o h} \int_{\frac{\pi}{-2}}^{\frac{\pi}{2}} \cos \theta d \theta \\ & E^{\prime}=\frac{\lambda}{4 \pi \epsilon_o h}\left(\sin \frac{\pi}{2}-\sin \left(-\frac{\pi}{2}\right)\right) \\ & E^{\prime}=\frac{\lambda}{4 \pi \epsilon_o h} \times 2 \\ & E^{\prime}=\frac{\lambda}{2 \pi \epsilon_o h}\end{aligned}$
This is the net electric field due to a long wire with linear charge density λ at a distance h from it.
In the question, linear charge density =E
Therefore
$E'=\frac{E}{2\pi \epsilon_o h}$
Answer:
Given that a proton and a neutron consist of three quarks each.
And, ‘up’ quark is of charge + $\left ( \frac{2}{3} \right )$ e, and the ‘down’ quark of charge $\left (- \frac{1}{3} \right )$ e
Let the number of 'up' quarks be n. Therefore, the number of 'down' quarks is (3-n).
$\therefore$ The net charge = $\\ n\times\frac{2}{3}e + (3-n)\frac{-1}{3}e = (n-1)e$
Now, a proton has a charge +1e
$\therefore$ $(n-1)e = +1e \implies n =2$
Proton will have 2 u and 1 d, i.e, uud
Similarly, the neutron has a charge 0
$\therefore$ $(n-1)e = 0 \implies n =1$
Neutron will have 1 u and 2 d, i.e, udd
Answer:
For equilibrium to be stable, there must be a restoring force, and hence all the field lines should be directed inwards towards the null point. This implies that there is a net inward flux of the electric field. But this violates Gauss's law, which states that the flux of the electric field through a surface not enclosing any charge must be zero. Hence, the equilibrium of the test charge cannot be stable.
Therefore, the equilibrium is necessarily unstable.
Answer:
Two charges of the same magnitude and sign are placed at a certain distance apart. The mid-point of the line joining these charges will have E =0.
When a test charge is displaced along the line towards the charges, it experiences a restoring force(which is the condition for stable equilibrium). But if the test charge is displaced along the normal of the line, the net electrostatic force pushes it away from the starting point. Hence, the equilibrium is unstable.
Answer:
Let s be the vertical deflection, t be the time taken by the particle to travel between the plates
$\therefore$ $s = ut + \frac{1}{2}at^2$
Here, u =0, since initially there was no vertical component of velocity.
The particle in the electric field will experience a constant force (Since the electric field is constant).
F = ma = -qE (Using Newton's Second Law, F = ma)
$\therefore$ a = -qE/m (-ve sign implies here in downward direction)
Again, t = Distance covered/ Speed = $L/ v_{x}$
(In x-direction, since there is no force, the component of velocity in x-direction remains constant = $v_{x}$.
And, the distance covered in the x-direction = length of the plate = L)
Putting these values in our deflection equation,
$\\ s = ut + \frac{1}{2}at^2 = (0)(L/v_{x}) + \frac{1}{2}(-qE/m)(L/v_{x})^2 \\ \implies s =\frac{-qEL^2}{2mv_{x}^2}$
(S is -ve, which implies it deflects downwards.)
$\therefore$ The vertical deflection of the particle at the far edge of the plate is $\frac{qEL^{2}}{2mv_{x}^{2}}$.
This motion is similar to the motion of a projectile in a gravitational field, which is also a constant force. The force acting on the particle in the gravitational field is mg, while in this case, it is qE. The trajectory will be the same in both cases.
Answer:
$\therefore$ The vertical deflection of the particle at the far edge of the plate is $s=\frac{qEL^{2}}{2mv_{x}^{2}}$
given s= 0.5cm=0.005cm
Calculate L from the above equation
$L=\sqrt{\frac{2smv_x^2}{qE}}=\sqrt{\frac{2\times 0.005\times 9.1\times 10^{-31}(2\times10^6)^2 }{1.6\times 10^{-19}\times9.1\times10^2}}$
L=1.6 cm
Class 12 Physics Chapter 1 - Electric Charges and Fields: Topics And Subtopics
Chapter 1 Electric Charges and Fields in Class 12 Physics introduces the fundamental concepts of electrostatics, focusing on how electric charges interact and create electric fields. This chapter lays the groundwork for understanding electric forces, Coulomb's law, and field lines.
1.1 Introduction
1.2 Electric Charge
1.3 Conductors and Insulators
1.4 Basic Properties of Electric Charge
1.4.1 Additivity of Charges
1.4.2 Charge Is Conserved
1.4.3 Quantisation of Charge
1.5 Coulomb’s Law
1.6 Forces Between Multiple Charges
1.7 Electric Field
1.7.1 Electric Field Due to a System of Charges
1.7.2 Physical Significance of Electric Field
1.8 Electric Field Lines
1.9 Electric Flux
1.10 Electric Dipole
1.10.1 The Field of an Electric Dipole
1.10.2 Physical Significance of Dipoles
1.11 Dipole in a Uniform External Field
1.12 Continuous Charge Distribution
1.13 Gauss’s Law
1.14 Applications of Gauss’s Law
1.14.1 Field Due to an Infinitely Long Straight Uniformly Charged Wire
1.14.2 Field Due to a Uniformly Charged Infinite Plane Sheet
1.14.3 Field Due to a Uniformly Charged Thin Spherical Shell
Class 12 Physics Chapter 1 - Electric Charges and Fields: Important Formulas
Electric Charges and Fields class 12 question answers: Important Formulas compile all the key equations and expressions from the chapter in one place, making revision quick and efficient. These formulas cover concepts like Coulomb's law, electric field intensity, electric potential, and Gauss's law, helping students solve problems with accuracy and speed.
Electric Charge (q)
1. Charge is a fundamental property of matter.
2. SI Unit: Coulomb (C)
3. Charge Quantization: $q=n e$ (where $n$ is an integer, $e=1.6 \times 10^{-19} \mathrm{C}$ )
Coulomb's Law
The force between two point charges at a distance r is given by:

$
F=k \frac{\left|q_1 q_2\right|}{r^2}
$
where $k=\frac{1}{4 \pi f_0} \approx 9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2$
Electric Field (E)
1. The electric field at a point due to an electric charge $q$ :
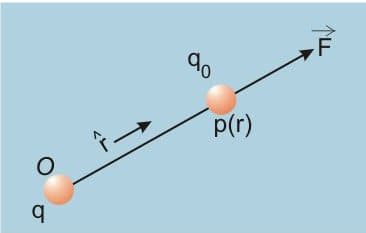
$
E=\frac{F}{q}=k \frac{q}{r^2}
$
2. For an electric Dipole at the Axial Position:
$
E=\frac{1}{4 \pi \varepsilon_0} \times \frac{2 p}{r^3}
$
3. For an electric Dipole at the Equatorial Position:
$
E=\frac{1}{4 \pi \varepsilon_0} \times \frac{p}{r^3}
$
Electric Dipole and Dipole Moment (p)
1. Dipole Moment: $p=q \times d$
2. Torque on a Dipole in a Uniform Electric Field:
$
\tau=p E \sin \theta
$
Electric Field Due to a Continuous Charge Distribution
1. Linear Charge Density $(\lambda): \lambda=\frac{q}{l}$
2. Surface Charge Density ( $\sigma$ ): $\sigma=\frac{q}{A}$
3. Volume Charge Density ( $\rho$ ): $\rho=\frac{q}{V}$
Gauss's Law
The total electric flux through a closed surface is:
$
\oint \mathbf{E} \cdot d \mathbf{A}=\frac{q}{\varepsilon_0}
$
Applications of Gauss's Law
1. Electric field due to an infinite line charge:
$
E=\frac{\lambda}{2 \pi \varepsilon_0 r}
$
2. Electric field due to a uniformly charged infinite plane:
$
E=\frac{\sigma}{2 \varepsilon_0}
$
3. Electric field due to a charged spherical shell:
Inside the shell: $E=0$
Outside the shell: $E=\frac{1}{4 \pi \varepsilon_0} \times \frac{q}{r^2}$
Approach to Solve the Questions of Class 12 Physics Chapter 1: Electric Charges and Fields
In order to answer the questions in Chapter 1 - Electric Charges and Fields of Physics Class 12, students should properly know the fundamentals of electrostatics and apply the formulas. This chapter contains both conceptual and numerical questions thus, the important part is to develop logical arguments and accuracy. Using a systematic approach is beneficial in addressing derivations, definitions and problem-based questions effectively when taking exams.
- Begin with a simple concept of electric charge, the different types of charges and the way the charges interact by the laws of electrostatics.
- Revise the Coulomb Law, and do some numerical problems based on the inverse-square relationships between charges.
- Revise the concept of electric field and field lines, and imagine the behaviour of the field around positive and negative charges.
- Learn about the concept of an electric dipole, learn about dipole moment, electric field due to a dipole, and the torque of a dipole in a uniform field.
- Revise derivations of electric flux and the Law of Gauss, as these are frequently appearing questions on the board exam.
- Use the Gauss Law to find solutions to both numerical and conceptual problems of charge distributions that are symmetrical, such as spheres, cylinders and planes.
- To solve problems, units, the direction of vectors, and diagrams should be paid attention to, as they enhance the clarity of the concepts.
- Lastly, revise all equations and do mixed questions of the NCERT exercises to gain speed and confidence to do exams.
How Can NCERT Solutions for Class 12 Physics Chapter 1 Help in Exam Preparation?
NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields help students understand the fundamentals of electrostatics in a clear, structured, and exam-oriented way. The Electric Charges and Fields NCERT Solutions make it easier to understand fundamental concepts, such as electric charge, Coulomb law, electric field, electric flux and Gauss law, which are the backbone of many physics problems. Dealing with definitions, derivations, and numerical problems one by one, Electric Charges and Fields NCERT Solutions simplify the visualisation and the application of such abstract concepts as field lines and flux. With frequent practice with these solutions, confidence regarding solving derivations, field-based numericals and conceptual questions that are commonly given in CBSE board exams, JEE and NEET is developed. The accuracy and the speed of problem-solving are also enhanced with regular usage of the Electric Charges and Fields class 12 question answers, and the clarity of concepts becomes well-developed. Such focused preparation provides a solid background to the next chapters of electrostatics, like Electrostatic Potential and Capacitance, which provides a better understanding at a higher level, helps in achieving higher marks, and is helpful in the long term to remember the basics of physics.
Importance of NCERT Solutions for Class 12 Physics Chapter 1: Electric Charges and Fields
NCERT Solutions for Class 12 Physics Chapter 1 Electric Charges and Fields are essential for understanding the fundamentals of electrostatics, which form the starting point of Class 12 Physics. The concepts presented in this chapter are very common in theoretical and numerical problems.
- Prepares students to grasp the clear vision of electric charge, Coulomb's law and the superposition principle.
- Gives a description of what electric field and electric field lines are in a straightforward and organised way.
- Establishes a solid basis for progressing topics in electrostatics, which includes electric potential, capacitance, and electric current.
- Plays a crucial role in CBSE board exams, where derivations and numerical problems from this chapter are frequently asked.
- Very crucial in competitive tests such as JEE and NEET because most of the questions are based on the electric field and the law of Gauss.
- Make students visualise and use Gauss's Law for symmetrical distributions of charge.
- Facilitates proper use of formulas and concepts of the various physical scenarios that involve electric charges and fields.
Improves problem-solving skills through step-by-step numerical solutions and clear derivations.
What Extra Should Students Study Beyond NCERT for JEE/NEET?
To score well in JEE and NEET, students must work beyond the NCERT syllabus with higher-level questions and be good at application-based concepts as well. The main differences in the additional preparation required to prepare for JEE and NEET are brought out in the table below.
NCERT Solutions for Class 12 Physics: Chapter Wise
NCERT Solutions for Class 12 Physics: Chapter-wise Links provide a structured pathway to access detailed solutions for every chapter in the syllabus. These solutions help students understand concepts clearly, improve problem-solving skills, and prepare effectively for board exams and competitive tests.
Also, check NCERT Books and NCERT Syllabus here:
- NCERT Books Class 12 Physics
- NCERT Syllabus Class 12 Physics
- NCERT Books Class 12
- NCERT Syllabus Class 12
NCERT solutions subject-wise
Frequently Asked Questions (FAQs)
Understanding electric charges and fields is fundamental to learning about electricity, electromagnetism, and how electric forces act at a distance—important for everything from electronics to physics research.
Electric charges are present in many daily phenomena, like static electricity, lightning, photocopiers, and electronic devices.
Many conceptual and numerical questions on Coulomb’s Law, electric field, and the superposition principle are frequently asked in NEET and JEE exams.
Yes, at certain points due to symmetry or superposition of fields, the net electric field can be zero.
The net charge inside a conductor is zero because charges redistribute on the surface. If the charge is zero then the electric field must be zero
NCERT Solutions breaks down difficult electrostatics problems into simple steps by offering detailed explanations for all in-text questions and exercises.
The chapter covers potential energy problems for charge systems, dipole moment calculations, electric field calculations at different distances, and Coulomb's law calculations for the force between point charges. Additionally, students apply Gauss's law for symmetric shapes, work with moving charges through electric fields, and solve problems involving fields caused by continuous charge distributions.
The NCERT Solutions offer step-by-step answers to all the in-text questions and exercises and reduce complex problems in electrostatics into small steps. The systematised problem-solving methods are necessary to calculate the electric fields and apply the law of Coulomb to develop conceptual clarity.
The solutions describe electric field lines as imaginary curves, the tangent of which at any point would provide the direction of the electric field, and line density would be the strength of the field. Field lines visualise the patterns of electric fields, which give students the patterns of fields surrounding various patterns of charges.
Questions related to CBSE Class 12th
On Question asked by student community
Hello
You will be able to download the CBSE Previous Year Board Question Papers from our official website, careers360, by using the link given below.
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers
I hope this information helps you.
Thank you.
Hello
You will be able to download the CBSE Pre-Board Class 12 Question Paper 2025-26 from our official website by using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-pre-board-class-12-question-paper-2025-26
I hope this information helps you.
Thank you.
Hello,
Yes, it's completely fine to skip this year's 12th board exams and give them next year as a reporter or private candidate, allowing you to prepare better; the process involves contacting your current school or board to register as a private candidate or for improvement exams during the specified
HELLO,
Yes i am giving you the link below through which you will be able to download the Class 12th Maths Book PDF
Here is the link :- https://school.careers360.com/ncert/ncert-book-for-class-12-maths
Hope this will help you!
Failing in pre-board or selection tests does NOT automatically stop you from sitting in the CBSE Class 12 board exams. Pre-boards are conducted by schools only to check preparation and push students to improve; CBSE itself does not consider pre-board marks. What actually matters is whether your school issues your
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
