NCERT Solutions for Class 12 Physics Chapter 9 - Ray Optics and Optical Instruments

Q 9.1 A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?

Answer:

Given, size of the candle, h = 2.5 cm

Object distance, u = 27 cm

The radius of curvature of the concave mirror, R = -36 cm

focal length of a concave mirror = R/2 = -18 cm

let image distance = v

now, as we know

$\frac{1}{u}+\frac{1}{v}=\frac{1}{f}$

$\frac{1}{-27}+\frac{1}{v}=\frac{1}{-18}$

$\frac{1}{v}=\frac{1}{-18} + \frac{1}{27}$

$v= -54cm$

now, let the height of image be $h'$

magnification of the image is given by

$m=\frac{h'}{h}=-\frac{v}{u}$

from here

${h'}=-\frac{-54}{-27}*2.5=-5cm$

Hence the size of the image will be -5cm. negative sign implies that the image is inverted and real

if the candle is moved closer to the mirror, we have to move the screen away from the mirror in order to obtain the image on the screen. if the image distance is less than the focal length image cannot be obtained on the screen and image will be virtual.

Ray Optics and Optical Instruments Excercise:

Question:

Q 9.2 A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.

Answer:

Given, the height of needle, h = 4.5 cm

distance of object = 12 cm

focal length of convex mirror = 15 cm.

Let the distance of the image be v

Now as we know

$\frac{1}{u}+\frac{1}{v}=\frac{1}{f}$

$\frac{1}{v}=\frac{1}{f} - \frac{1}{u}$

$\frac{1}{v}=\frac{1}{15} - \frac{1}{-12}$

$\frac{1}{v}=\frac{1}{15} + \frac{1}{12}$

v = 6.7 cm

Hence the distance of the image is 6.7 cm from the mirror and it is on the other side of the mirror.

Now, let the size of the image be h'

so.

$m=-\frac{v}{u} = \frac{h'}{h}$

$h'= -\frac{v}{u}*h$

$h'= -\frac{6.7}{-12}*4.5$

$h'= 2.5 cm$

Hence the size of the image is 2.5 cm. positive sign implies the image is erect, virtual and diminished.

Magnification of the image = $\frac{h'}{h}$ = $\frac{2.5}{4.5}$ = 0.56

m = 0.56

The image will also move away from the mirror if we move the needle away from the mirror, and the size of the image will decrease gradually.

Q 9.3 A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? If water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again?

Answer:

Given:

Actual height of the tank,h = 12.5 cm

Apparent height of tank,h' = 9.4 cm

let refrective index of the water be $\mu$

$\mu = \frac{h}{h'} =\frac{12.5}{9.4} = 1.33 (approx)$

so the refractive index of water is approximately 1.33.

Now, when water is replaced with a liquid having $\mu = 1.63$

$\mu = \frac{h}{h'} =\frac{12.5}{h'_{new}} = 1.63$

$h'_{new}= \frac{12.5}{1.63}= 7.67 cm$

Hence the new apparent height of the needle is 7.67 cm.

Total distance we have to move in a microscope = 9.4 - 7.67 = 1.73 cm.

Since new apparent height is lesser than the previous apparent height we have to move UP the microscope in order to focus the needle.

Q 9.4 Figures of (a) and (b) show refraction of a ray in air incident at $60^{\circ}$ with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is $45^{\circ}$ with the normal to a water-glass interface [Fig.(c)].

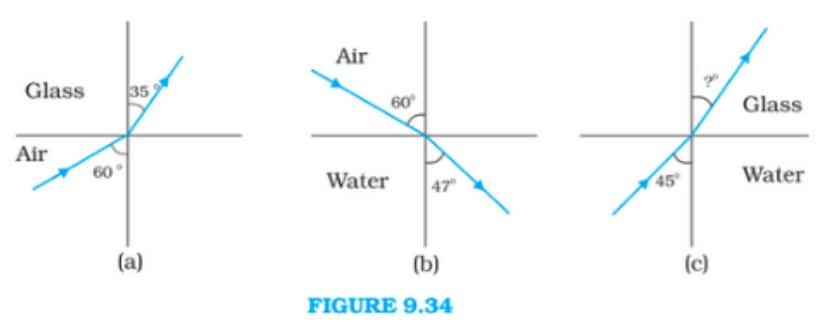
Answer:

As we know, by Snell's law

$\mu_1\sin\theta _1=\mu _2\sin\theta _2$ where,

$\mu_1$ = refrective index of medium 1

$\theta _1$ = incident angle in medium 1

$\mu _2$ = refrective index of medium 2

$\theta _2$ = refraction angle in medium 2

Now, applying it for fig (a)

$1\sin 60=\mu _{glass}\sin 35$

$\mu _{glass}=\frac{\sin 60}{\sin 35}=\frac{0.866025}{0.573576 } = 1.509$

Now applying for fig (b)

$1\sin 60=\mu _{water}\sin 47$

$\mu _{water}=\frac{\sin 60}{\sin 47}=\frac{.8660}{.7313} = 1.184$

Now in fig (c) Let refraction angle be $\theta$ so,

$\mu _{water}\sin 45=\mu _{glass}\sin\theta$

$\sin\theta =\frac{\mu _{water}*\sin 45}{\mu _{glass}}$

$\sin\theta =\frac{1.184*0.707}{1.509} = 0.5546$

$\theta = \sin^{-1}(0.5546) = 38.68$

Therefore the angle of refraction when ray goes from water to glass in fig(c) is 38.68.

Q 9.5 A small bulb is placed at the bottom of a tank containing water to a depth of 80cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)

Answer:

Rays of light will emerge out in all direction and upto the angle when total internal reflection starts i.e. when the angle of refraction is 90 degree.

let the incident angle be i when refraction angle is 90 degree.

so, by Snell's law

$\mu _{water}\sin i=1\sin 90$

from here, we get

$\sin i=\frac{1}{1.33}$

$i=\sin^{-1}(\frac{1}{1.33})=48.75^0$

Now Let R be Radius of the circle of the area from which the rays are emerging out. and d be the depth of water which is = 80 cm.

From the figure:

$tani=\frac{R}{d}$

$R = tani*d=tan48.75^0*80cm$

R = 91 cm

So the area of water surface through which rays will be emerging out is

$\Pi R^2 = 3.14*(91)^2cm^2$

$= 2.61m^2$

therefore required area $= 2.61m^2$ .

Q 9.6 A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be $40^{\circ}$ . What is the refractive index of the material of the prism? The refracting angle of the prism is $60^{\circ}$ . If the prism is placed in water, predict the new angle of minimum deviation of a parallel beam of light.

Answer:

In Prism :

Prism angle ( $A$ ) = First Refraction Angle ( $r _1$ ) + Second refraction angle ( $r _2$ )

also, Deviation angle ( $\delta$ ) = incident angle( $i$ ) + emerging angle( $e$ ) - Prism angle ( $A$ ) ..............(1)

the deviation angle is minimum when the incident angle( $i$ ) and an emerging angle( $e$ ) are the same. in other words

$i=e$ ...........(2)

from (1) and (2)

$\delta_{min} = 2i-A$

$i=\frac{\delta_{min} +A}{2}$ ..........................(3)

We also have

$r _1 = r_2 = r = \frac{A}{2}$ .................(4)

Now applying snells law using equation (3) and (4)

$\mu _1\sin i=\mu _2\sin r$

$1\sin(\frac{\delta _{min}+A}{2})=\mu _2\sin\frac{A}{2}$

$\mu _2=\frac{\sin(\frac{\delta _{min}+A}{2})}{\sin\frac{A}{2}}$ ...................(5)

Given

$\\\delta _{min}= 40 \\A = 60$

putting those values in (5) we get

$\mu _2=\frac{\sin(\frac{40+60}{2})}{\sin\frac{60}{2}}=\frac{\sin 50}{\sin 30}=1.532$

Hence the refractive index of the prism is 1.532.

Now when the prism is in the water.

Applying Snell's law:

$\mu _1\sin(\frac{\delta _{min}+A}{2})=\mu _2\sin\frac{A}{2}$

$1.33\sin(\frac{\delta _{min}+60}{2})=1.532\sin\frac{60}{2}$

$\sin(\frac{\delta _{min}+60}{2})=\frac{1.532*0.5}{1.33}$

$\frac{\delta _{min}+60}{2}=\sin^{-1}\frac{1.532*0.5}{1.33}$

$\delta _{min} =2\sin^{-1}0.5759 - 60$

$\delta _{min} =2*35.16- 60 =10.32^0$

Hence minimum angle of deviation inside water is 10.32 degree.

Q 9.7 Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20cm?

Answer:

As we know the lens makers formula

$\frac{1}{f}=(\mu _{21}-1)(\frac{1}{R_1}-\frac{1}{R_2})$

[ This is derived by considering the case when the object is at infinity and image is at the focus]

Where $f$ = focal length of the lens

$\mu _{21}$ = refractive index of the glass of lens with the medium(here air)

$R_1$ and $R_2$ are the Radius of curvature of faces of the lens.

Here,

Given, $f$ = 20cm,

$R_1$ = $R$ and $R_2$ = $-R$

$\mu _{21}$ = 1.55

Putting these values in te equation,

$\frac{1}{20}=(1.55-1)(\frac{1}{R}-\frac{1}{-R})$

$\frac{2}{R}=\frac{1}{20}*\frac{1}{0.55}$

$R = 40*0.55$

$R = 22cm$

Hence Radius of curvature of the lens will be 22 cm.

Q 9.8 A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20cm, and (b) a concave lens of focal length 16cm?

Answer:

In any Lens :

$\frac{1}{v} - \frac{1}{u}=\frac{1}{f}$

$\\v=$ the distance of the image from the optical centre

$\\u=$ the distance of the object from the optical centre

$\\f=$ the focal length of the lens

a)

Here, The beam converges from the convex lens to point P. This image P will now act as an object for the new lens which is placed 12 cm from it and focal length being 20 cm.

So,

$\frac{1}{v} - \frac{1}{12}=\frac{1}{20}$

$\frac{1}{v}=\frac{1}{20} + \frac{1}{12}$

$\frac{1}{v}=\frac{8}{60}$

$v = 7.5 cm$

Hence distance of image is 7.5 cm and it will form towards the right as the positive sign suggests.

b)

Here, Focal length $f$ = -16cm

so,

$\frac{1}{v} - \frac{1}{12}=\frac{1}{-16}$

$\frac{1}{v} =\frac{1}{-16} + \frac{1}{12} = \frac{1}{48}$

$v = 48 cm$

Hence image distance will be 48 cm in this case, and it will be in the right direction(as the positive sign suggests)

Q 9.9 An object of size 3.0cm is placed 14cm in front of a concave lens of focal length 21cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens?

Answer:

In any Lens;

$\frac{1}{v} - \frac{1}{u}=\frac{1}{f}$

$\\v=$ the distance of the image from the optical centre

$\\u=$ the distance of the object from the optical centre

$\\f=$ the focal length of the lens

Here Given,

$\\u=$ -14 cm

$\\f=$ -21 cm

$\frac{1}{v} - \frac{1}{-14}=\frac{1}{-21}$

$\frac{1}{v} =\frac{1}{-21}- \frac{1}{14} = \frac{-5}{42}$

$v = -\frac{42}{5}= -8.4cm$

Hence image distance is -8.4 cm. the negative sign indicates the image is erect and virtual.

Also as we know,

$m= -\frac{v}{u} = \frac{h'}{h}$

From Here

$h'= -\frac{v}{u}h$

$h'= -\frac{-8.4}{-12}*3= 1.8 cm$

Hence the height of the image is 1.8 cm.

As we move object further away from the lens, the image will shift toward the focus of the lens but will never go beyond that. Size of the object will decrease as we move away from the lens.

Q 9.10 What is the focal length of a convex lens of focal length 30cm in contact with a concave lens of focal length 20cm? Is the system a converging or a diverging lens? Ignore the thickness of the lenses.

Answer:

When two lenses are in contact the equivalent is given by

$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}$

where $f_1$ and $f_2$ are the focal length of two individual lenses.

So, Given,

$f_1 =$ 30 cm and $f_2 = -20cm$ (as focal length of the convex lens is positive and of the concave lens is negative by convention)

putting these values we get,

$\frac{1}{f}=\frac{1}{30}+\frac{1}{-20}$

$\frac{1}{f}=-\frac{1}{60}$

$f = -60cm$

Hence equivalent focal length will be -60 cm and since it is negative, equivalent is behaving as a concave lens which is also called diverging lens.

Q 9.11 A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15cm. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision (25cm), and (b) at infinity? What is the magnifying power of the microscope in each case?

Answer:

In a compound microscope, first, the image of an object is made by the objective lens and then this image acts as an object for eyepiece lens.

Given

the focal length of objective lens = $f_{objective}$ = 2 cm

focal length of eyepiece lense = $f_{eyepiece}$ = 6.25cm

Distance between the objective lens and eyepiece lens = 15 cm

a)

Now in Eyepiece lense

Image distance = $v_{final}$ = -25 cm (least distance of vision with sign convention)

focal length = $f_{eyepiece}$ = 6.25 cm

$\frac{1}{f_{eyepiece}} = \frac{1}{v_{final}} - \frac{1}{u}$

$\frac{1}{u} = \frac{1}{v_{final}} -\frac{1}{f_{eyepiece}}$

$\frac{1}{u} = \frac{1}{-25} -\frac{1}{6.25} = -\frac{1}{5}$

$u = -5 cm.$

Now, this object distance $u$ is from the eyepiece lens since the distance between lenses is given we can calculate this distance from the objective lens.

the distance of $u$ from objective lens = $d+u=$ $15 - 5=10cm$ . This length will serve as image distance for the objective lens.

$v = 10 cm$

so in the objective lens

$\frac{1}{f_{objective}} = \frac{1}{v} - \frac{1}{u_{initial}}$

$\frac{1}{u_{initial}} = \frac{1}{v} - \frac{1}{f_{objective}}$

$\frac{1}{u_{initial}} = \frac{1}{10} - \frac{1}{2} = -\frac{4}{10}=-\frac{2}{5}$

$u_{intial}$ = -2.5 cm

Hence the object distance required is -2.5 cm.

Now, the magnifying power of a microscope is given by

$m=\frac{v}{|u_{initial}|}(1+\frac{d}{f_{eyepiece}})$ where $d$ is the least distance of vision

so putting these values

$m=\frac{10}{2.5}(1+\frac{25}{6.25}) = 20$

Hence the lens can magnify the object to 20 times.

b) When image is formed at infinity

in eyepiece lens,

$\frac{1}{f_{eyepiece}} = \frac{1}{v_{final}} - \frac{1}{u}$

$\frac{1}{6.25} = \frac{1}{infinity} - \frac{1}{u}$

from here $u =$ - 6.25., this distance from objective lens = $d+u$ = 15 - 6.25 = 8.75 = $v$

in the optical lens:

$\frac{1}{f_{objective}} = \frac{1}{v} - \frac{1}{u_{initial}}$

$\frac{1}{2} = \frac{1}{-6.25} - \frac{1}{u_{initial}}$

$\frac{1}{u_{initial}} =- \frac{6.75}{17.5}$

$u_{initial}=-2.59cm$

Now,

$m=\frac{v}{|u_{initial}|}(1+\frac{d}{f_{eyepiece}})$ where $d$ is the least distance of vision

putting the values, we get,

$m=\frac{8.75}{2.59}(1+\frac{25}{6.25})= 13.51$

Hence magnifying power, in this case, is 13.51.

Q 9.12 A person with a normal near point (25 cm) using a compound microscope with objective of focal length 8.0 mm and an eyepiece of focal length 2.5cm can bring an object placed at 9.0mm from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope

Answer:

Inside a microscope,

For the eyepiece lens,

$\frac{1}{f_{eyepiece}}=\frac{1}{v_{eyepiece}} - \frac{1}{u_{eyepiece}}$

we are given

$v_{eyepiece}= -25cm$

$f_{eyepiece}= 2.5cm$

$\frac{1}{2.5}=\frac{1}{-25} - \frac{1}{u_{eyepiece}}$

$\frac{1}{u_{eyepiece}}=\frac{1}{-25} - \frac{1}{2.5}=-\frac{11}{25}$

$u_{eyepiece}=- \frac{25}{11}=-2.27cm$

we can also find this value by finding image distance in the objective lens.

So, in objective lens

$\frac{1}{f_{objective}}=\frac{1}{v_{objective}} - \frac{1}{u_{objective}}$

we are given

$f_{objective}= 0.8$

$u_{objective}= -0.9$

$\frac{1}{0.8}=\frac{1}{v_{objective}} - \frac{1}{-0.9}$

$\frac{1}{v_{objective}} = \frac{0.1}{0.72}$

$v_{objective} = 7.2cm$

Distance between object lens and eyepiece = $|u_{eyepiece}| + v_{objective}$ = 2.27 + 7.2 = 9.47 cm.

Now,

Magnifying power :

$m = \frac{v_{obejective}}{|u_{objective}|}(1+\frac{d}{f_{eyepiece}})$

$m = \frac{7.2}{0.9}(1+\frac{25}{2.5})= 88$

Hence magnifying power for this case will be 88.

Q 9.13 A small telescope has an objective lens of focal length 144cm and an eyepiece of focal length 6.0cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece?

Answer:

The magnifying power of the telescope is given by

$m=\frac{f_{objective}}{f_{eyepiece}}$

Here, given,

focal length of objective lens = $f_{objective}=$ 144 cm

focal length of eyepiece lens = $f_{eyepiece}=$ 6 cm

$m=\frac{f_{objective}}{f_{eyepiece}}=\frac{144}{6}=24$

Hence magnifying power of the telescope is 24.

in the telescope distance between the objective and eyepiece, the lens is given by

$d= f_{objective}+ f_{eyepiece}$

$d = 144+6=150$

Therefore, the distance between the two lenses is 250 cm.

Q 9.14 (a) A giant refracting telescope at an observatory has an objective lens of focal length 15m. If an eyepiece of focal length 1.0cm is used, what is the angular magnification of the telescope?

Answer:

Angular magnification in the telescope is given by :

angular magnification = $\alpha =$ $\frac{f_{objective} }{f_{eyepiece}}$

Here given,

focal length of objective length = 15m = 1500cm

the focal length of the eyepiece = 1 cm

so, angular magnification, $\alpha =$ $\frac{1500}{1}$

$\alpha = 1500$

Q 9.14 (b) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is $3.48 \times 106m$ , and the radius of the lunar orbit is $3.8 \times 108m$ .

Answer:

Given,

The radius of the lunar orbit,r = $3.8 \times 108m$ .

The diameter of the moon,d = $3.48 \times 106m$

focal length $f = 15m$

let $d_1$ be the diameter of the image of the moon which is formed by the objective lens.

Now,

the angle subtended by diameter of the moon will be equal to the angle subtended by the image,

$\frac{d}{r}=\frac{d_1}{f}$

$\frac{3.48*10^6}{3.8*10^8}=\frac{d_1}{15}$

$d_1=13.74 cm$

Hence the required diameter is 13.74cm.

Q 9.15 (a) Use the mirror equation to deduce that:

an object placed between f and 2f of a concave mirror produces a real image beyond 2f.

Answer:

The equation we have for a mirror is:

$\frac{1}{f}=\frac{1}{v}+\frac{1}{u}$

$\frac{1}{u}=\frac{1}{f}-\frac{1}{v}$

Given condition $f<u<2f$ and $v>2f$

$\frac{1}{2f}<\frac{1}{u}<\frac{1}{f}$ and $\frac{1}{v}<\frac{1}{2f}$

$-\frac{1}{2f}>-\frac{1}{u}>-\frac{1}{f}$

$\frac{1}{f}-\frac{1}{2f}>\frac{1}{f}-\frac{1}{u}>\frac{1}{f}-\frac{1}{f}$

$\frac{1}{2f}>\frac{1}{v}>0$

${2f}<{v}<0$

Here $f$ has to be negative in order to satisfy the equation and hence we conclude that our mirror is a concave Mirror. It also satisfies that $-v>-2f$ (image lies beyond 2f)

Q. 9.15 (b) Use the mirror equation to deduce that:

a convex mirror always produces a virtual image independent of the location of the object.

Answer:

In a convex mirror focal length is positive conventionally.

so we have mirror equation

$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$

$\frac{1}{v}= \frac{1}{f}-\frac{1}{u}$

Here, since object distance is always negative whenever we put our object in the left side of the convex mirror(which we always do, generally). So $\frac{1}{v}$ is always the sum of two positive quantity(negative sign in the equation and negative sign of the $u$ will always make positive) and hence we conclude that $v$ is always greater than zero which means the image is always on the right side of the mirror which means it is a virtual image. Therefore, a convex lens will always produce a virtual image regardless of anything.

Q 9.15 (c) Use the mirror equation to deduce that:

the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.

Answer:

In a convex mirror focal length is positive conventionally.

so we have mirror equation

$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$

$\frac{1}{v}= \frac{1}{f}-\frac{1}{u}$

here since $f$ is positive and $u$ is negative (conventionally) so we have,

$\frac{1}{v}>\frac{1}{f}$ that is '

$v<f$

which means the image will always lie between pole and focus.

Now,

$\frac{1}{v}= \frac{1}{f}-\frac{1}{u}=\frac{u-f}{uf}$

$magnification (m)=-\frac{v}{u} = \frac{f}{f-u}$

here since $u$ is always negative conventionally, it can be seen that magnification of the image will be always less than 1 and hence we conclude that image will always be diminished.

Q 9.15 (d) Use the mirror equation to deduce that:

an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.

Answer:

The focal length $f$ of concave mirror is always negative.

Also conventionally object distance $u$ is always negative.

So we have mirror equation:

$\frac{1}{f} = \frac{1}{v}+\frac{1}{u}$

$\frac{1}{v}=\frac{1}{f}-\frac{1}{u}$

Now in this equation whenever $u<f$ , $\frac{1}{v}$ will always be positive which means $v$ is always positive which means it lies on the right side of the mirror which means image is always virtual.

Now,

$m=-\frac{v}{u}=-\frac{f}{u-f}$

since the denominator is always less than the numerator, so the magnitude magnification will always be greater than 1

Hence we conclude that image is always gonna be enlarged.

Hence an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.

Q 9.16 A small pin fixed on a table top is viewed from above from a distance of 50cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?

Answer:

As we know,

Refractive index =

$\frac{actualdepth}{apparentdepth}$

Here actual depth = 15cm

let apparent depth be d'

And refractive index of the glass = 1.5

now putting these values, we get,

$1.5 = \frac{15}{d'}$

$d' =10$

the change in the apparent depth = 15 - 10 = 5 cm.

as long as we are not taking slab away from the line of sight of the pin, the apparent depth does not depend on the location of the slab.

Q 9.17 (a) In the following f igure shows a cross-section of a ‘light pipe’ made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.

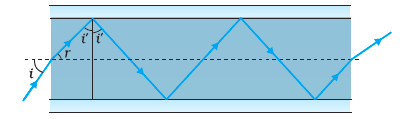
Answer:

We are given,

Refractive index of glass( $\mu _{glass}$ ) and outer covering( $\mu _{outerlayer}$ ) is 1.68 and 1.44 respectively.

Now applying snell's law on upper glass - outer layer,

$\mu _{glass}\sin i'=\mu_{outerlayer}\sin 90$

$i' =$ the angle from where total Internal reflection starts

$\sin i'=\frac{\mu_{outerlayer}}{\mu_{glass}} = \frac{1.44}{1.68}=0.8571$

$i' = 59^0$

At this angle, in the air-glass interface

Refraction angle $r$ = 90 - 59 = 31 degree

let Incident Angle be $i$ .

Applying Snell's law

$1\sin i=\mu_{glass}\sin r$

$\sin i=1.68\sin 31=0.8652$

$i=60$ (approx)

Hence total range of incident angle for which total internal reflection happens is $0<i<60$

Q 9.17 (b) What is the answer if there is no outer covering of the pipe?

Answer:

In the case when there is no outer layer,

Snell's law at glass-air interface(when the ray is emerging out from the pipe)

$\mu _{glass}\sin i'=1\sin 90$

$\sin i'=\frac{1}{\mu_{glass}} = \frac{1}{1.68}=0.595$

$i'=$ 36.5

refractive angle $r$ corresponding to this = 90 - 36.5 = 53.5.

the angle r is greater than the critical angle

So for all of the incident angles, the rays will get total internally reflected.in other words, rays won't bend in air-glass interference, it would rather hit the glass-air interference and get reflected

Q 9.18 The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?

Answer:

As we know for real image, the maximum focal length is given by

$f_{max}= \frac{d}{4}$

where d is the distance between the object and the lens.

So putting values we get,

$f_{max}= \frac{3}{4}=0.75$

Hence maximum focal length required is 0.75.

Q 9.19 A screen is placed 90cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20cm. Determine the focal length of the lens.

Answer:

As we know that the relation between focal length $f$ , the distance between screen $D$ and distance between two locations of the object $d$ is :

$f=\frac{D^2-d^2}{4D}$

Given: $D$ = 90 cm., $d$ = 20 cm ,

so

$f=\frac{90^2-20^2}{4*90}$

$f=\frac{90^2-20^2}{4*90}=\frac{770}{36}=21.39cm$

Hence the focal length of the convex lens is 21.39 cm.

Q 9.20 (a) Determine the ‘effective focal length’ of the combination of the two lenses in Exercise 9.10, if they are placed 8.0cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of effective focal length of this system useful at all?

Answer:

Here there are two cases, first one is the one when we see it from convex side i.e. Light are coming form infinite and going into convex lens first and then goes to concave lens afterwords. The second case is a just reverse of the first case i.e. light rays are going in concave first.

1)When light is incident on convex lens first

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

$\frac{1}{v}=\frac{1}{f}+\frac{1}{u}$

$\frac{1}{v}=\frac{1}{30}+\frac{1}{infinite}$

$v= 30cm$

Now this will act as an object for the concave lens.

$\frac{1}{f_{concave}}=\frac{1}{v_{fromconcave}}-\frac{1}{u_{fromconcave}}$

$u_{fromconcave}= 30 - 8 = 22 cm$

$\frac{1}{-20}=\frac{1}{v_{fromconcave}}-\frac{1}{22}$

$\frac{1}{v}=-\frac{1}{220}$

$v = -220cm$

Hence parallel beam of rays will diverge from this point which is (220 - 4 = 216) cm away from the centre of the two lenses.

2) When rays fall on the concave lens first

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

$\frac{1}{v}=\frac{1}{f}+\frac{1}{u}$

$\frac{1}{v}=\frac{1}{-20}+\frac{1}{infinite}$

$v=-20cm$

Now this will act as an object for convex lens.

$\frac{1}{f_{convex}}=\frac{1}{v_{fromconvex}}-\frac{1}{u_{fromconvex}}$

$u_{fromconvex}= -20-8=-28cm$

$\frac{1}{-30}=\frac{1}{v_{fromconvex}}-\frac{1}{-28}$

$\frac{1}{v_{fromconvex}}=\frac{1}{30}-\frac{1}{28}=-\frac{1}{420}$

$v_{fromconvex}= -420cm$

Hence parallel beam will diverge from this point which is (420 - 4 = 146 cm ) away from the centre of two lenses.

As we have seen for both cases we have different answers so Yes, answer depend on the side of incidence when we talk about combining lenses. i .e. we can not use the effective focal length concept here.

Q 9.21 At what angle should a ray of light be incident on the face of a prism of refracting angle $60^{\circ}$ so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is $1.524$ .

Answer:

Let prism be ABC ,

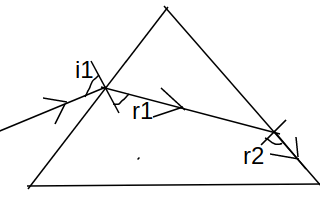
as emergent angle $e=90^0$ ,

$\mu_{glass}\sin r_2 = 1\sin 90$

$\sin r_2=\frac{1}{1.524} = 0.6562$

$r_2= 41 ^0$ (approx)

Now as we know in the prism

$r_1+r_2=A$

Hence, $r_1+=A-r_2=60-41=19^0$

Now applying snells law at surface AB

$1\sin i=\mu _{glass}\sin r_1$

$\sin i=1.524\sin 19$

$sini=0.496$

$i = 29.75^0$

Hence the angle of incident is 29.75 degree.

Q 9.22 A card sheet divided into squares each of size 1 mm 2 is being viewed at a distance of 9 cm through a magnifying glass (a converging lens of focal length 10 cm) held close to the eye.

(a) What is the magnification produced by the lens? How much is the area of each square in the virtual image?

(b) What is the angular magnification (magnifying power) of the lens?

(c) Is the magnification in (a) equal to the magnifying power in (b)? Explain.

Answer:

Given,

Object distance u = -9cm

Focal length of convex lens = 10cm

According to the lens formula

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

$\frac{1}{10}=\frac{1}{v}-\frac{1}{-9}$

$\\\frac{1}{v}=\frac{1}{10}-\frac{1}{9}\\\Rightarrow v=-90\ cm$

a) Magnification

$m=\frac{v}{u}=\frac{-90}{9}=10 \ cm$

The area of each square in the virtual image

$=10\times10\times1=100mm^2=1cm^2$

b) Magnifying power

$=\frac{d}{|u|}=\frac{25}{9}=2.8$

c) No,

$magnification = \frac{v}{u}$

$magnifying\ power = \frac{d}{|u|}$ .

Both the quantities will be equal only when image is located at the near point |v| = 25 cm

Answer the question

Q 9.25 (a) The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?

Answer:

Angular magnification is the ratio of tangents of the angle formed by object and image from the centre point of the lens. In this question angle formed by the object and a virtual image is same but it provides magnification in a way that, whenever we have object place before 25cm, the lens magnifies it and make it in the vision range. By using magnification we can put the object closer to the eye and still can see it which we couldn't have without magnification.

Answer the question

Q 9.25. (b) In viewing through a magnifying glass, one usually positions one’s eyes very close to the lens. Does angular magnification change if the eye is moved back?

Answer:

Yes, angular magnification will change if we move our eye away from the lens. this is because then angle subtended by lens would be different than the angle subtended by eye. When we move our eye form lens, angular magnification decreases. Also, one more important point here is that object distance does not have any effect on angular magnification.

Answer the question?

Q 9.25 (c) Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power?

Answer:

Firstly, grinding a lens with very small focal length is not easy and secondly and more importantly, when we reduce the focal length of a lens, spherical and chronic aberration becomes more noticeable. they both are defects of the image, resulting from the ways of rays of light.

Q 9.25 Answer the Question?

(d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths?

Answer:

We need more magnifying power and angular magnifying power in a microscope in order to use it effectively. Keeping both objective focal length and eyepiece focal length small makes the magnifying power greater and more effective.

Answer the Question?

Q 9.25 (e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why? How much should be that short distance between the eye and eyepiece?

Answer:

When we view through a compound microscope, our eyes should be positioned a short distance away from the eyepiece lens for seeing a clearer image. The image of the objective lens in the eyepiece lens is the position for best viewing. It is also called "eye-ring" and all reflected rays from lens pass through it which makes it the ideal position for the eye for the best view.

When we put our eyes too close to the eyepiece lens, then we catch the lesser refracted rays from eyes, i.e. we reduce our field of view because of which the clarity of the image gets affected.

Q9.26 An angular magnification (magnifying power) of 30X is desired using an objective of focal length 1.25cm and an eyepiece of focal length 5cm. How will you set up the compound microscope?

Answer:

Given,

magnifying power = 30

objective lens focal length

$f_{objeective}$ = 1.25cm

eyepiece lens focal length

$f_{eyepiece}$ = 5 cm

Normally, image is formed at distance d = 25cm

Now, by the formula;

Angular magnification by eyepiece:

$m_{eyepiece}=1+\frac{d}{f_{eyepiece}}=1+\frac{25}{5}=6$

From here, magnification by the objective lens :

$m_{objective}=\frac{30}{6}=5$ since ( $m_{objective}*m_{eyepiece}=m_{total}$ )

$m_{objective}=-\frac{v}{u}=5$

$v=-5u$

According to the lens formula:

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

$\frac{1}{1.25}=\frac{1}{-5u}-\frac{1}{u}$

from here,

$u = -1.5cm$

hence object must be 1.5 cm away from the objective lens.

$v= -mu=(-1.5)(5)=7.5$

Now for the eyepiece lens:

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

$\frac{1}{5}=\frac{1}{-25}-\frac{1}{u}$

$\frac{1}{u}=-\frac{6}{25}$

$u = -4.17 cm$

Hence the object is 4.17 cm away from the eyepiece lens.

The separation between objective and eyepiece lens

$u_{eyepiece} +v_{objectivve}=4.17 + 5.7 = 11.67 cm$

Q 9.27 (a) A small telescope has an objective lens of focal length 140cm and an eyepiece of focal length 5.0cm. What is the magnifying power of the telescope for viewing distant objects when
(a) the telescope is in normal adjustment (i.e., when the final image is at infinity)?

Answer:

Given,

the focal length of the objective lens $f_{objective}=140cm$

the focal length of the eyepiece lens $f_{eyepiece}=5cm$

normally, least distance of vision = 25cm

Now,

As we know magnifying power:

$m = \frac{f_{objective}}{f_{eyepiece}}=\frac{140}{5}=28$

Hence magnifying power is 28.

Q 9.27 (b) A small telescope has an objective lens of focal length 140cm and an eyepiece of focal length 5.0cm. What is the magnifying power of the telescope for viewing distant objects when

(b) the final image is formed at the least distance of distinct vision (25cm)?

Answer:

Given,

the focal length of the objective lens $f_{objective}=140cm$

the focal length of the eyepiece lens $f_{eyepiece}=5cm$

normally, least distance of vision = 25cm

Now,

as we know magnifying power when the image is at d = 25 cm is

$m=\frac{f_{objective}}{f_{eyepiece}}(1+\frac{f_{eyepiece}}{d})=\frac{140}{5}(1+\frac{5}{25}) = 33.6$

Hence magnification, in this case, is 33.6.

Q 9.28 (a) For the telescope described in Exercise 9.27 (a), what is the separation between the objective lens and the eyepiece?

Answer:

a) Given,

focal length of the objective lens = $f_{objective}$ = 140cm

focal length of the eyepiece lens = $f_{eyepiece}$ = 5 cm

The separation between the objective lens and eyepiece lens is given by:

$f_{eyepiece}+f_{objective}=140+5=145cm$

Hence, under normal adjustment separation between two lenses of the telescope is 145 cm.

Q 9.28 (b) If this telescope is used to view a 100 m tall tower 3 km away, what is the height of the image of the tower formed by the objective lens?

Answer:

Given,

focal length of the objectove lens = $f_{objective}$ = 140cm

focal length of the eyepiece lens = $f_{eyepiece}$ = 5 cm

Height of tower $h_{tower}$ = 100m

Distance of object which is acting like a object $u$ = 3km = 3000m.

The angle subtended by the tower at the telescope

$tan\theta=\frac{h_{tower}}{u}=\frac{100}{3000}=\frac{1}{30}$

Now, let the height of the image of the tower by the objective lens is $h_{image}$ .

angle made by the image by the objective lens :

$tan\theta'=\frac{h_{image}}{f_{objective}}=\frac{h_{image}}{140}$

Since both, the angles are the same we have,

$tan\theta=tan\theta'$

$\frac{1}{30}=\frac{h_{image}}{140}$

$h_{image}= \frac{140}{30}=4.7cm$

Hence the height of the image of the tower formed by the objective lens is 4.7 cm.

Q 9.28 (c) What is the height of the final image of the tower if it is formed at 25cm

Answer:

Given, image is formed at a distance $d$ = 25cm

As we know, magnification of eyepiece lens is given by :

$m=1+\frac{d}{f_{eyepiece}}$

$m=1+\frac{25}{5}=6$

Now,

Height of the final image is given by :

$h_{image}= mh_{object}= 6*4.7 = 28.2cm$

Therefore, the height of the final image will be 28.2 cm

Q9.29 A Cassegrain telescope uses two mirrors as shown in Fig. 9.26. Such a telescope is built with the mirrors 20mm apart. If the radius of curvature of the large mirror is 220mm and the small mirror is 140mm, where will the final image of an object at infinity be?

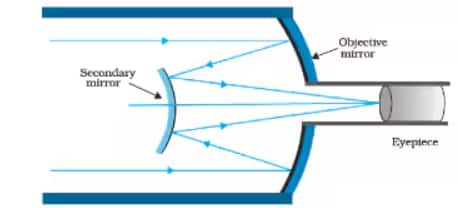
Answer:

Given,

Distance between the objective mirror and secondary mirror $d= 20mm$

The radius of curvature of the Objective Mirror

$R_{objective}=220mm$

So the focal length of the objective mirror

$f_{objective}=\frac{220}{2}=110mm$

The radius of curvature of the secondary mirror

$R_{secondary}=140mm$

so, the focal length of the secondary mirror

$f_{secondary}=\frac{140}{2}=70mm$

The image of an object which is placed at infinity, in the objective mirror, will behave like a virtual object for the secondary mirror.

So, virtual object distance for the secondary mirror

$u_{secondary}=f_{objective}-d=110-20=90mm$

Now, applying the mirror formula in the secondary mirror:

$\frac{1}{f}=\frac{1}{v}+\frac{1}{u}$

$\frac{1}{v}=\frac{1}{f}-\frac{1}{u}$

$\frac{1}{v}=\frac{1}{70}-\frac{1}{90}$

$v=315mm$

Q 9.30 Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in Fig. 9.29. A current in the coil produces a deflection of 3.5 o of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?

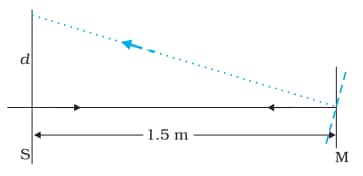
Answer:

Given

Angle of deflection $\delta = 3.5^0$

The distance of the screen from the mirror $D=1.5m$

The reflected rays will bet deflected by twice angle of deviation that is

$2\delta =3.5*2=7^0$

Now from the figure, it can be seen that

$tan2\delta =\frac{d}{1.5}$

$d=1.5*\tan2\delta = 2*\tan7=0.184m=18.4cm$

Hence displacement of the reflected spot of the light is $18.4cm$ .

Q 9.31 Figure 9.30 shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid?

Answer:

Given

The focal length of the convex lens $f_{convex}=30cm$

here liquid is acting like the mirror so,

the focal length of the liquid $=f_{liquid}$

the focal length of the system(convex + liquid) $f_{system}=45cm$

Equivalent focal length when two optical systems are in contact

$\frac{1}{f_{system}}=\frac{1}{f_{convex}}+\frac{1}{f_{liquid}}$

$\frac{1}{f_{liquid}}=\frac{1}{f_{system}}-\frac{1}{f_{convex}}$

$\frac{1}{f_{liquid}}=\frac{1}{45}-\frac{1}{30}=-\frac{1}{90}$

$f_{liquid}=-90cm$

Now, let us assume refractive index of the lens be $\mu _{lens}$

The radius of curvature are $R$ and $-R$ .

As we know,

$\frac{1}{f_{convex}}=(\mu _{lens}-1)\left ( \frac{1}{R}-\frac{1}{-R} \right )$

$\frac{1}{f_{convex}}=(\mu _{lens}-1)\frac{2}{R}$

$R=2(\mu _{lens-1})f_{convex}=2(1.5-1)30=30cm$

Now, let refractive index of liquid be $\mu _{liquid}$

The radius of curvature of liquid in plane mirror side = infinite

Radius of curvature of liquid in lens side R = -30cm

As we know,

$\frac{1}{f_{liquid}}=(\mu_{liquid-1})\left ( \frac{1}{R}-\frac{1}{infinite} \right )$

$-\frac{1}{90}=(\mu_{liquid}-1)(\frac{1}{30})$

$\mu_{liquid}= 1+\frac{1}{3}$

$\mu_{liquid}= 1.33$

Therefore the refractive index of the liquid is 1.33.

Class 12 Physics NCERT Chapter 9: Higher Order Thinking Skills (HOTS) Questions

Q.1 A convex lens mode of glass (refractive index $=$ 1.5) has a focal length 24 cm in air. When it is totally immersed in water (refractive index $=1.33$ ), its focal length changes to
Answer:
$
\begin{aligned}
& \frac{1}{8}=\left(\frac{\mu_{\ell}}{\mu_{\mathrm{s}}}-1\right)\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right] \\
& \frac{1}{24}=(1.5-1)\left[\frac{2}{\mathrm{R}}\right] ---(i)\\
& \frac{1}{\mathrm{f}^{\prime}}=\left(\frac{1.5}{1.33}-1\right)\left(\frac{2}{\mathrm{R}}\right) \\
& \frac{1}{\mathrm{f}^{\prime}}=\left(\frac{1.5 \times 3}{4}-1\right) \frac{2}{\mathrm{R}}---(ii)
\end{aligned}
$
(i) divided by (ii)
$\begin{aligned} & \frac{\mathrm{f}^{\prime}}{24}=4 \\ & \mathrm{f}^{\prime}=96 \mathrm{~cm} \\ & \text { }\end{aligned}$

Q.2 An Ice cube has a bubble inside. when viewed from one side the apparent distance of the bubble is $24 \mathrm{~cm}$. When viewed from the opposite side, the apparent distance of the bubble is observed as $2 \mathrm{~cm}$. If the side of the ice cube is $48 \mathrm{~cm}$. The refractive index of the cube is (answer should be the nearest integer)
Answer:

let side of the cube is $x$

refractive index $=n$
$
n=\frac{\text { true depth }}{\text { App depth }}
$

When viewing the bubble from one ide, the depth is $x$ and the apparent depth is $24 \mathrm{~cm}$.

$ n=\frac{x}{24} ......(i) $

When viewing the bubble from the opposite side, the true depth is $48-x$

(since the side of the cube is $48 \mathrm{cm})$. and the apparent depth in $2 \mathrm{~cm}$.

$n=\frac{48-x}{2}.....(ii)$

from i and ii

$
\begin{aligned}
\frac{x}{24} & =\frac{48-x}{2} \\
\frac{x}{12} & =48-x \\
x & =576-12 x \\
13 x & =576 \\
x & =\frac{576}{13} \\
x & =44.3 \approx 44
\end{aligned}
$

So,
$
n=\frac{44}{12}=\frac{11}{3}=3.67
$

The nearest integer is 4

so n=4

Q.3 A point object is moving with a speed of v before an arrangement of two mirrors as shown in the figure.

Find the velocity of image in mirror $\mathrm{M}_1$ with respect to image in mirror $\mathrm{M}_2$

Answer:

Velocity of image, $\mathrm{v}_{\mathrm{r}}=\sqrt{\mathrm{v}^2+\mathrm{v}^2-2 \mathrm{v} \cdot \mathrm{v} \cdot \cos \theta}=2 \mathrm{v} \sin (\theta / 2)$

Q.4 A metal plate is lying at the bottom of a tank full of a transparent liquid. Height of tank is 100cm but the plate appears to be at 45 cm above bottom. The refractive index of liquid is:
Answer:
Real depth of plate, $\mathrm{H}=100 \mathrm{~cm}$
The apparent depth of the plate, $\mathrm{h}=100-45=55 \mathrm{~cm}$
$\therefore$ The refractive index of the fluid $=\frac{\mathrm{H}}{\mathrm{h}}=\frac{100}{55}=1.81$

Q. 5 Two lenses are placed in contact with each other and the focal length of the combination is 80cm. If the focal length of one is 20cm, then the power of the other will be:

Answer:

The focal length of the combination,

$
\begin{aligned}
& \frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}_1}+\frac{1}{\mathrm{f}_2} \Rightarrow \frac{1}{80}=\frac{1}{20}+\frac{1}{\mathrm{f}_2} \\
& \therefore \mathrm{f}_2=-\frac{80}{3} \mathrm{~cm}
\end{aligned}
$

$\therefore \quad$ Power of second lens $\mathrm{P}^{\prime}=\frac{100}{\mathrm{f}_2}=\frac{100}{(-80 / 3)}=-3.75 \mathrm{D}$