Have you ever noticed your hair, basically just standing up after you rub a balloon ,or when dust seems to stick to a television screen? Those tiny, everyday happenings look ordinary but they are actually tied to electrostatic forces . NCERT Solution for Class 12 Physics Chapter 1, Electric Charges and Fields will help students get the idea in a way that feels more clear, and also more organized.
This Story also Contains
In this write-up, you can find the full NCERT Solutions as per the latest CBSE syllabus. It takes care of the main points including electric charge, the properties that come with charge, Coulomb’s law, electric field along with field lines , the electric dipole, electric flux, and then Gauss’s law. Besides the theory part, there are step-by-step answers for NCERT questions , plus some extra practice questions, HOTS questions, and important formulas that you can revise quickly. You will also be able to download PDF notes and get short, easy explanations for numericals so accuracy and speed both improve. Whether you’re aiming for board exams or you’re preparing for JEE/NEET, this guide should help you build solid concepts, not just memorize things, and it will give you more confidence in electrostatics.
The NCERT Class 12 Physics Chapter 1 - Electric Charges and Fields question answers are available in an easy-to-download PDF format for quick and effective revision. These class 12 physics chapter 1 Electric Charges and Fields question answers cover all the important concepts like Coulomb's Law, electric field, flux, and Gauss's Law, with clear, step-by-step explanations. Students can download the free NCERT Solutions for Class 12 Physics Chapter 1 PDF to access detailed answers anytime, making exam preparation and practice more convenient.
Also, Read -
The Electric Charges and Fields class 12 question answers offer a solution to each question in the exercises of the chapter and allow students to gain a robust knowledge of electrostatics. Important concepts such as Coulomb's law, electric field, electric flux, and Gauss theorem are explained with the right words in these class 12 physics chapter 1 Electric Charges and Fields questions answers, hence preparing to undertake exams easily.
Answer:
Given,
$q_{1}$ = $2 \times 10^{-7}$ C
$q_{2}$ = $3 \times 10^{-7}C$
r = 30 cm = 0.3 m
We know,
The force between two charged particles, $q_{1}$ and $q_{2}$ separated by a distance r.
$F = \frac{1}{4\pi \epsilon _{0}} \frac{q_{1}q_{2}}{r^2}$
$ \Rightarrow F= \frac{1}{4\pi \epsilon _{0}} \frac{2\times10^{-7} \times 3 \times 10^{-7}}{(30\times10^{-2}\ m)^2\ }$
$\Rightarrow F= (9\times10^9\ N)\times \frac{6\times10^{-14+4}}{900\ m^2\ } = 6\times10^{-3} N$
Since the charges are of the same nature, the force is repulsive.
Answer:
Given,
$q_{1}$ = $0.4 \mu C$
$q_{2}$ = $-0.8 \mu C$
F = $-0.2N$ (Attractive)
We know,
The force between two charged particles, $q_{1}$ and $q_{2}$, separated by a distance r.
$F = \frac{1}{4\pi \epsilon _{0}} \frac{q_{1}q_{2}}{r^2}$
$\Rightarrow \\ -0.2 = 9\times10^9 \times \frac{(0.4\times10^{-6})(-0.8\times10^{-6})}{r^2} \\$
$\implies r^2 = 9\times10^9\times0.32\times10^{-12}/0.2 \\$
$\implies r^2 = 9\times0.16\times10^{-2} \\$
$\implies r = 1.2\times10^{-1} m = 0.12 m =12 cm$
Therefore, the distance between the two charged spheres is 12 cm.
Answer:
Using Newton's third law, the force exerted by the spheres on each other will be equal in magnitude.
Therefore, the force on the second sphere due to the first = 0.2 N
(This force will be attractive since charges are of opposite sign.)
Answer:
Electrostatic force
$F=\frac{KQ^2}{r^2}$
So the dimension of
$[Ke^2]=[Fr^2]$ ..................(1)
The gravitational force between two bodies of mass M and m is
$F=\frac{GMm}{r^2}$
So, the dimension of
$[Gm_em_p]=[Fr^2]$ .............(2)
Therefore, from (1) and (2)
$[\frac{ke^{2}}{Gm_{e}m_{p}} ]$ is dimensionless
Here,
K = $1/4\pi \epsilon _{0}$ , where $\epsilon _{0}$ is the permittivity of space.
$[1/ \epsilon _{0}] =[C/V.m] = [Nm^2 C^{-2}]$
e = Electric charge ([e] = [C])
G = Gravitational constant. ([G]= $[Nm^2kg^{-2}]$ )
$m_{e}$ and $m_{p}$ are mass of electron and proton ([ $m_{e}$ ] = [ $m_{p}$ ] = [Kg])
Substituting these units, we get
$[\frac{ke^{2}}{Gm_{e}m_{p}} ] = [\frac{C^2 \times Nm^2C^{-2}}{Nm^2kg^{-2}\times kg\times kg} ] = M^{0}L^{0}T^{0}$
Hence, this ratio is dimensionless.
Putting the value of the constants
$\frac{ke^{2}}{Gm_{e}m_{p}} = \frac{9\times10^9\times(1.6\times10^{-19})^{2}}{6.67\times10^{11}\times9.1\times10^{-31}\times1.67\times10^{-27}}=2.3 \times 10^{40}$
The given ratio is the ratio of the electric force $\frac{ke^{2}}{R^2}$ to the gravitational force between an electron and a proton $\frac{Gm_{e}m_{p}}{R^2}$, considering the distance between them is constant!
Q 1.4 (a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
Answer:
The given statement "electric charge of a body is quantised" implies that the charge on a body can take only integral values. In other words, only an integral number of electrons can be transferred from one body to another and not in fractions.
Therefore, a charged body can only have an integral multiple of the electric charge of an electron.
Answer:
On a macroscopic level, the amount of charge transferred is very large compared to the charge of a single electron. Therefore, we tend to ignore the quantisation of electric charge in these cases and consider it to be continuous in nature.
Answer:
When a glass rod is rubbed with a silk cloth, opposite charges appear on both the rod and the cloth.
The phenomenon of charging bodies by rubbing them against each other is known as charging by friction. Here, electrons are transferred from one body to another, giving both bodies an equal but opposite charge. The number of electrons lost by one body (attains a positive charge due to loss of negatively charged electrons) is equal to the number of electrons gained by the other body (attains a negative charge). Therefore, the net charge of the system is zero. This is in accordance with the law of conservation of charge
Answer:
Charges at (A, C) and (B, D) are pairwise diametrically opposite and also equal.
Therefore, their force on a point charge at the centre of the square will be equal but opposite in direction.
Now, AC = BD = $\sqrt{2}\times(10\times10^{-2} m) = \sqrt{2}\times0.1 m$
$\therefore$ AO = BO = CO = DO = r = Half of diagonal = $\sqrt{2}\times0.05 m$
Force on point charge at centre due to charges at A and C = $F_{A} = -F_{C} = \frac{k(2\mu C)(1\mu C)}{(r)^2}$
Similarly, force on point charge at centre due to charges at B and D = $F_{B} = -F_{D} = \frac{k(-5\mu C)(1\mu C)}{(r)^2}$
$\therefore$ Net force on point charge = $\\F_{A} + F_{B} + F_{C} + F_{D} = -F_{B} +F_{B} - F_{D} + F_{D} = 0$ .
Hence, the charge at the centre experiences no force.
Answer:
A positive point charge experiences a force in an electrostatic field. Since the charge will experience a continuous force and cannot jump from one point to another, the electric field lines must be continuous.
Q 1.7 (b) Explain why two field lines never cross each other at any point.
Answer:
A tangent drawn at any point on a field line gives the direction of force experienced by a unit positive charge due to the electric field at that point. If two lines intersect at a point, then the tangent drawn there will give two directions of force, which is not possible. Hence, two field lines cannot cross each other at any point.
Answer:
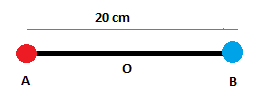
Given, AB = 20 cm
Since O is the midpoint of the line AB.
AO = OB = 10 cm = 0.1m
The electric field at a point caused by charge q is given as,
$E = \frac{kq}{r^2}$
Where q is the charge, r is the distance between the charges and the point O
k = 9x109 N m2 C -2
Now,
Due to the charge at A, the electric field at O will be $E_{A}$ and in the direction AO.
$E_{A} =\frac{ 9\times10^9 \times 3\times10^{-6}}{0.1^2}$
Similarly, the electric field at O due to the charge at B is also in the direction AO
$E_{B} =\frac{ 9\times10^9 \times (-3\times10^{-6})}{0.1^2}$
Since both the forces are acting in the same direction, we can add their magnitudes to get the net electric field at O:
E' = $E_{A}$ + $E_{B}$ = 2E (Since their magnitudes are same)
$E' =2\times \frac{ 9\times10^9 \times 3\times10^{-6}}{0.1^2} = 5.4\times 10^4 N/C$ along the direction AO.
Answer:
Let Q = $-1.5 \times10^{-9}$ C
The force experienced by Q when placed at O due to the charges at A and B will be:
$F = Q \times E$
where 'E' is the net electric field at point O.
$F=1.5 \times 10^{-9} C \times 5.4 \times 10^4 N/C = 8.1\times10^{-3 } N$
Q, being negatively charged, will be attracted by the positive charge at A and repelled by the negative charge at B. Hence, the direction of force experienced by it will be in the direction of OA.
Answer:
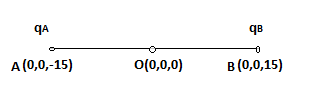
Given,
$q_{A}=2.5\times 10^{-7}C$ and $q_{B}=-2.5\times 10^{-7}$
The total charge of the system = $q_{A} + q_{B} = 0$
$\therefore$ The system is electrically neutral. (All dipole systems have net charge zero!)
Now, distance between the two charges, d = 15 + 15 = 30 cm = 0.3 m
We know, the electric dipole moment of the system, p = $q_{A}$ x d = $q_{B}$ x d (i.e, the magnitude of charge x distance between the two charges)
$\therefore p = 2.5\times10^{-7} C \times 0.3 m = 7.5\times10^{-8} Cm$
The direction of a dipole is towards the positive charge. Hence, in the positive z-direction.
Answer:
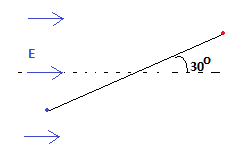
Given,
Electric dipole moment, p = $4\times 10^{-9} Cm$
$\theta = 30^{0} \ \therefore sin\theta = 0.5$
E = $5\times 10^{4}NC^{-1}$
We know that the torque acting on a dipole is given by:
$\tau = p \times E$
$\implies \tau = p Esin\theta = 4\times10^{-9} \times5\times10^{4}\times0.5 \ Nm$
$\implies \tau =10^{-4}Nm$
Therefore, the magnitude of torque acting on the dipole is $10^{-4}Nm$
Answer:
Clearly, polyethene being negatively charged implies that it has an excess of electrons(which are negatively charged!). Therefore, electrons were transferred from wool to polyethene.
Given, charge attained by polyethene = $-3\times 10^{-7}$ C
We know, Charge on 1 electron = $-1.6\times10^{-19} C$
Therefore, the number of electrons transferred to attain a charge of $-3\times 10^{-7} =\frac{-3\times 10^{-7}}{-1.6\times10^{-19} C} = 1.8\times10^{12}$ electrons.
Answer:
The charge attained by polyethene (and also wool!) is solely due to the transfer of free electrons.
We know, Mass of an electron = $9.1\times10^{-31}\ kg$
The total mass of electrons transferred = number of electrons transferred x mass of an electron
= $9.1\times10^{-31} \times 1.8\times10^{12}\ kg = 16.4\times10^{-19} \ kg$
Yes, there is a transfer of mass, but it is negligible.
Answer:
Since the radii of the spheres A and B are negligible compared to the distance of separation, we consider them as a point object.
Given,
charge on each of the spheres = $6.5\times 10^{-7}C$
and distance between them, r = 50 cm = 0.5 m
We know,
$F = k\frac{q_{1}q_{2}}{r^2}$
Therefore, the mutual force of electrostatic repulsion(since they have the same sign of charge)
$F = 9\times10^9Nm^{2}C^{-2}\times\frac{(6.5\times10^{-7}\ C)^2}{(0.5\ m )^2} = 1.5\times10^{-2} N$
Answer:
We know that the force between two charged particles separated by a distance r is:
$F = k\frac{q_{1}q_{2}}{r^2} = k\frac{q^2}{r^2}$ $(\because q_{1} = q_{2} = q)$
Now if $q\rightarrow 2q\ and\ r\rightarrow r/2$
The new value of force:
$F_{new} =k\frac{(2q)^2}{(r/2)^2} = 16k\frac{q^2}{r^2} = 16F$
Therefore, the force increases 16 times!
$F_{new} =16F = 16\times1.5\times10^{-2} N = 0.24\ N$
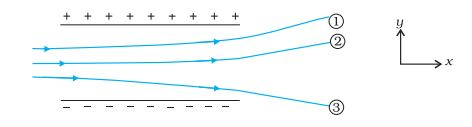
Answer:
Charges 1 and 2 are repelled by the negatively charged plate of the system
Hence, 1 and 2 are negatively charged.
Similarly, 3 being repelled by the positive plate is positively charged.
(charge to the mass ratio: charge per unit mass)
Since 3 is deflected the most, it has the highest charge-to-mass ratio.
Answer:
Given,
$E=3\times 10^{3}\ \widehat{i}\ \frac{N}{C}$
Area of the square = $0.01^2\ m^2$
Since the square is parallel to the yz plane, its normal is in the x-direction.(i.e $\widehat{i}$ direction )
Therefore, flux through this surface:
$\phi = E.A$
$\implies \phi = (3\times10^3\ \widehat{i}).(0.01\ \widehat{i}) Nm^2/C = \boldsymbol{30 Nm^2/C}$
Answer:
Now, since the normal of the square plane makes a $60^{\circ}$ angle with the x-axis
$cos\Theta = cos(60^{0}) = 0.5$
Therefore, flux through this surface:
$\phi = E.A = EAcos\theta$
$\implies \phi = (3\times10^3)(0.01)(0.5) Nm^2/C = \boldsymbol{15\ Nm^2/C}$
Answer:
The net flux of the uniform electric field through a cube oriented so that its faces are parallel to the coordinate planes is zero.
This is because the number of lines entering the cube is the same as the number of lines leaving the cube.
Alternatively,
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
Since there is no charge enclosed in the cube, $\phi = 0$.
Answer:
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
Given, $\phi = 8.0 \times10^3\ Nm^2/C$
$\therefore q = \phi \times\epsilon _{0} = (8.0\times10^3 \times8.85\times10^{-12})\ C$
$\implies q = 70 \times10^{-9} C = \boldsymbol{0.07 \mu C}$
This is the net charge inside the box.
Answer:
Using Gauss's law, we know that $\phi = q/\epsilon _{0}$
Since flux is zero, q = 0, but this q is the net charge enclosed by the surface.
Hence, we can conclusively say that the net charge is zero, but we cannot conclude that there are no charges inside the box.
Answer:
Let us assume that the charge is at the centre of the cube with an edge of 10 cm.
Using Gauss's law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
Therefore, flux through the cube: $\phi = (10\times10^{-6} C)/\epsilon _{0}$
Due to symmetry, we can conclude that the flux through each side of the cube, $\phi'$, will be equal.
$\therefore \phi' = \frac{\phi}{6} = \frac{10^{-5}}{6\times\epsilon _{0}} = \frac{10^{-5}}{6\times\ 8.85\times10^{-12}} = \boldsymbol{1.9 \times 10^5\ Nm^2C^{-1}}$
Answer:
Given,
q = net charge inside the cube = $2.0\mu C$
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
$\therefore \phi = 2.0\times10^{-6}/8.85\times10^{-12}\ Nm^2C^{-1} = \boldsymbol{2.2\times10^5\ Nm^2C^{-1}}$
(Note: Using Gauss's formula, we see that the electric flux through the cube is independent of the position of the charge and the dimension of the cube! )
Answer:
Given,
$\phi = -1.0\times 10^{3}\frac{Nm^{2}}{C}$
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
Therefore, flux does not depend on the radius of the sphere but only on the net charge enclosed. Hence, the flux remains the same although the radius is doubled.
$\phi' = -10^{3}\frac{Nm^{2}}{C}$
Answer:
Given,
$\phi = -1.0\times 10^{3}\frac{Nm^{2}}{C}$
Using Gauss’s law, we know that the flux of the electric field through any closed surface S is $1/\epsilon _{0}$ times the total charge enclosed by S.
i.e. $\phi = q/\epsilon _{0}$
where, q = net charge enclosed and $\epsilon _{0}$ = permittivity of free space (constant)
$\therefore q = -10^{3}Nm^2C^{-1} \times 8.85\times10^{-12}N^{-1}m^{-2}C^{2} = -8.8\times10^{-9}\ C \\ = \boldsymbol{-8.8\ nC}$
Answer:
We know that, for determining the electric field at r>R for a conducting sphere, the sphere can be considered as a point charge located at its centre.
Also, the electric field intensity at a point P, located at a distance r, due to the net charge q is given by,
$E = k\frac{q}{r^2}$
Given, r = 20 cm = 0.2 m (From the centre, not from the surface!)
$\\ \therefore 1.5\times10^3 = 9\times10^9\times \frac{q}{0.2^2} \\ \implies q = \frac{1.5\times0.04}{9}\times10^{-6} = 6.67\times10^{-9}\ C$
Therefore, charge on the conducting sphere is $- 6.67\ nC$ (since flux is inwards)
Answer:
Given,
Surface charge density = $80.0\mu Cm^{-2}$
Diameter of sphere = 2.4 m $\therefore$ radius of sphere, r = 1.2 m
The charge on the sphere, Q = surface charge density x surface area of the sphere
$= (80\times10^{-6})\times(4\pi r^2) = 320\times22/7\times(1.2)^2 = \boldsymbol{1.45\times10^{-3}\ C}$
Answer:
Using Gauss's law, we know that :
$\phi = q/ \epsilon_{0}$
$\implies \phi = 1.45\times10^{-3}/ 8.85\times10^{-12} = 1.6\times10^{8}\ Nm^2C^{-1}$
Answer:
Given,
$\lambda = 9\times 10^{4}\frac{N}{C}$
d = 2 cm = 0.02 m
We know, for an infinite line charge having linear charge density $\lambda$, the electric field at a distance d is:
$E = k\lambda / d$
$\therefore 9\times10^4 = 9\times10^{9}\lambda / 0.02$
The linear charge density is $10 \mu C/cm$.
Answer:
We know the electric field, E, due to an infinite plate (length>>thickness) having surface charge density $\sigma$ = $\sigma/2\epsilon_{0}$.
(To note: It's independent of distance from the plate!)
In the region outside the first plate,
since both plates have the same surface charge density(in magnitude only), their electric fields are the same in magnitude in this region but opposite in direction.
(E due to positive plate away from it and E due to negative plate towards it!)
Hence, the electric field in the outer region of the first plate is zero.
Answer:
We know the electric field, E, due to an infinite plate (length>>thickness) having surface charge density $\sigma$ = $\sigma/2\epsilon_{0}$.
(To note: It's independent of distance from the plate and the same everywhere!)
In the region outside the second plate,
Since both plates have the same surface charge density(in magnitude only), their electric fields are the same in magnitude in this region but opposite in direction.
(E due to positive plate away from it and E due to negative plate towards it!)
Hence, the electric field in the outer region of the second plate is zero.
Answer:
We know the electric field, E, due to an infinite plate (length>>thickness) having surface charge density $\sigma$ = $\sigma/\epsilon_{0}$.
(To note: It's independent of distance from the plate!)
Let A and B be the two plates such that:
$\sigma_{A}= 17\times10^{-22} Cm^{-2}$ = $\sigma$
$\sigma_{B}= -17\times10^{-22} Cm^{-2}$ = - $\sigma$
Therefore,
The electric field between the plates, E = $E_{A} + E_{B}$ = $\sigma_{A}/2\epsilon_{0} + (-\sigma_{B}/2\epsilon_{0})$
$\Rightarrow E = \sigma/2\epsilon_{0} = 17\times10^{-22}/8.85\times10^{-12} = 1.92\times10^{-10 } NC^{-1}$
The NCERT Solutions for Class 12 Physics Chapter 1: Electric Charges and Fields include extra practice questions that help students strengthen their understanding of the chapter. These additional questions cover all important concepts like electric field, Coulomb’s law, and electric flux in an easy-to-understand way. Solving them regularly improves problem-solving skills and prepares students well for CBSE board exams and competitive tests like JEE and NEET.
Answer:
When two spheres of the same size are touched, on attaining the equipotential state, the total charge of the system is equally distributed on both of them.
Therefore, (i) When uncharged third sphere C is touched with A, charge left on A = $0.5\times 6.5\times 10^{-7}C$
and charge attained by C = $0.5\times 6.5\times 10^{-7}C$
(ii) Now, charge on B + charge on C = $6.5\times 10^{-7}C$ + $0.5\times 6.5\times 10^{-7}C$ = $1.5\times 6.5\times 10^{-7}C$
When touched, charge left on B = $0.5\times1.5\times 6.5\times 10^{-7}C$
Therefore $q_{A}\rightarrow 0.5\times q_{A}\ and\ q_{B}\rightarrow 0.75\times q_{B}$
Therefore,
$F' = 0.5\times0.75 \times F = 0.375 \times 1.5\times10^{-2} N = \boldsymbol{5.7\times10^{-3}\ N}$
Answer:
The force due to the electric field is balancing the weight of the oil droplet.
weight of the oil drop = density x volume of the droplet x g = $\rho \times \frac{4}{3}\pi r^3 \times g$
Force due to the electric field = E x q
charge on the droplet, q = No. of excess electrons x charge of an electron = $12\times q_{e} = 12\times 1.6\times10^{-19} = 1.92\times10^{-18} C$
Balancing forces:
$\rho \times \frac{4}{3}\pi r^3 \times g = E\times q$
Putting known and calculated values:
$\\ r^3 =\frac{3}{4\pi} E\times q / \rho\times g $
$ \Rightarrow r^3 = \frac{3}{4}\times\frac{7}{22}\times(2.55\times10^4)\times 1.92\times10^{-18} / (1.26\times10^3 \times10 ) $
$ \Rightarrow r^3 = 0.927\times10^{-18} m^3$
$r = 0.975\times10^{-6} m = 9.75\times10^{-4} mm$
Q 3. Which among the curves shown in Figure cannot possibly represent electrostatic field lines?
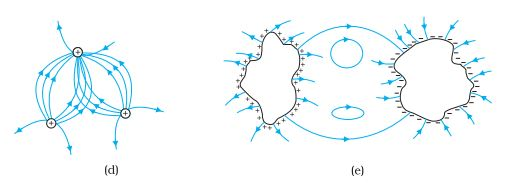
Answer:
(a) Wrong, because field lines must be normal to a conductor.
(b) Wrong, because field lines can only start from a positive charge. It cannot start from a negative charge,
(c) Right;
(d) Wrong, because field lines cannot intersect each other,
(e) Wrong, because electrostatic field lines cannot form closed loops.
Answer:
Force on a charge F=qE
But here E is varying along the Z direction.
Force can be written as,
$F=q\frac{dE}{dz}dz=P\frac{dE}{dz}=10^{-7}\times10^5=10^{-2}N$
Torque experienced =0 since both dipole and electric field are in the Z direction. The angle between the dipole and the electric field is 180 degrees
$\tau = \mathbf{p}\times \mathbf{E}=pE \sin 180=0$
Answer:
We know that the electric field inside a conductor is zero.
Using Gauss's law, if we draw any imaginary closed surface inside the solid, the net charge must be zero. (Since E = 0 inside)
Hence, there cannot be any charge inside the conductor, and therefore, all charge must appear on the outer surface of the conductor.
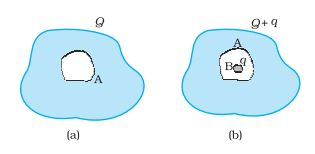
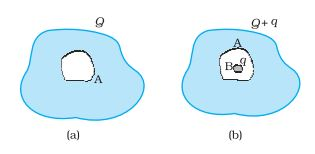
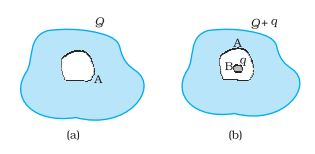
Answer:
We know that the electric field inside a conductor is zero.
Now, imagine a Gaussian surface just outside the cavity inside the conductor. Since E=0 (Using Gauss' law), the net charge must be zero inside the surface. Therefore, a -q charge is induced on the inner side of the cavity(facing conductor B).
Now consider a Gaussian surface just outside the conductor A. The net electric field must be due to charge Q and q. Hence, q charge is induced on the outer surface of conductor A. Therefore, the net charge on the outer surface of A is Q + q.
Answer:
We know that the electric field inside a conductor is zero.
Therefore, a possible way to shield from the strong electrostatic fields in its environment is to enclose the instrument fully by a metallic surface.
Answer:
Let the surface area of the sphere be S.
And assume that the hole is filled. For a point B, just above the hole, considering a Gaussian surface passing through B, we have
$\oint E.dS = q/\epsilon_{0}$
Now, since the electric field is always perpendicular to the surface of the conductor.
$\\ \therefore \oint E.dS = E.S= q/\epsilon_{0} = (\sigma.S)/\epsilon_{0} \\ \implies E = \sigma/\epsilon_{0}$
Using Superposition principle, $E =E_{1} + E_{2}$ ,
where $E_{1}$ is due to the hole and $E_{2}$ is due to the rest of the conductor. (both pointing outwards, i.e away from the centre)
Again, for a point A, just below the hole, the Electric field will be zero because of electrostatic shielding.
Using the superposition principle, this will be due to $E_{1}$ pointing inwards(towards the centre) and due to $E_{2}$ (Pointing away from the centre)
$0 =E_{1}-E_{2}$ $\implies E_{1}=E_{2}$
Using this relation, we get:
$E =E_{1} + E_{2} = 2E_{1} \implies E_{1} = E/2 = \sigma/2\epsilon_{0}$
Since this is pointing outwards,
$\boldsymbol{E_{1}} = \sigma/2\epsilon_{0}\ \boldsymbol{\widehat{n}}$ is the electric field in the hole.
(Trick:
1. Assume the hole to be filled.
2. Consider 2 points just above and below the hole.
3. Electric fields at these points will be due to the hole and the rest of the conductor. Use the superposition principle.)
[Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Answer:
Let AB be a long, thin wire of uniform linear charge density λ.
Let us consider the electric field intensity due to AB at point P at a distance h from it, as shown in the figure.
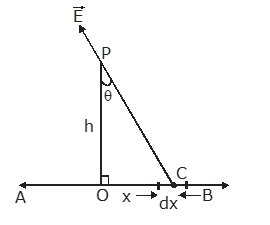
The charge on a small length dx on the line AB is q, which is given as q = λdx.
So, according to Coulomb’s law, the electric field at P due to this length dx is
$dE'=\frac{1}{4\pi \epsilon_o}\frac{\lambda dx}{(PC)^2}$
But $P C=\sqrt{h^2+x^2}$
$
\Rightarrow d E=\frac{1}{4 \pi \epsilon_o} \frac{\lambda d x}{\left(h^2+x^2\right)}
$
This electric field at P can be resolved into two components as dEcosθ and dEsinθ. When the entire length AB is considered, then the dEsinθ components add up to zero due to symmetry. Hence, there is only the dEcosθ component.
So, the net electric field at P due to dx is
dE' = dE cosθ
$
\Rightarrow d E^{\prime}=\frac{\lambda d x \cos \theta}{4 \pi \epsilon_o \left(h^2+x^2\right)}
$-----(1)
$\qquad$
$\ln \triangle \mathrm{POC}$
$
\tan \theta=\frac{x}{h}
$
$
\Rightarrow \mathrm{x}=\mathrm{h} \tan \theta
$
Differentiating both sides w.r.t. $\theta$,
$
\begin{aligned}
& \frac{d x}{d \theta}=h \sec ^2 \theta \\
& \Rightarrow \mathrm{dx}=\mathrm{h} \sec ^2 \theta \mathrm{~d} \theta .........(2)
\end{aligned}
$
Also, $h^2+x^2=h^2+h^2 \tan ^2 \theta$
$
\begin{aligned}
& \Rightarrow h^2+x^2=h^2\left(1+\tan ^2 \theta\right) \\
& \Rightarrow h^2+x^2=h^2 \sec ^2 \theta \ldots \ldots \ldots \ldots...........(3)
\end{aligned}
$
(Using the trigonometric identity, $1+\tan ^2 \theta=\sec ^2 \theta$ )
Using equations (2) and (3) in equation (1),
$
\begin{aligned}
& d E^{\prime}=\frac{\lambda \cos \theta \times h \sec ^2 \theta}{4 \pi \epsilon_o \times h^2 \sec ^2 \theta} d \theta \\
& d E^{\prime}=\frac{\lambda \cos \theta}{4 \pi \epsilon_o h} d \theta
\end{aligned}
$
The wire extends from $\theta=-\frac{\pi}{2}$ to $\theta=\frac{\pi}{2}$ since it is very long. Integrating both sides,
$
E^{\prime}=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\lambda \cos \theta}{4 \pi \epsilon_o h} d \theta
$
$\begin{aligned} & E^{\prime}=\frac{\lambda}{4 \pi \epsilon_o h} \int_{\frac{\pi}{-2}}^{\frac{\pi}{2}} \cos \theta d \theta \\ & E^{\prime}=\frac{\lambda}{4 \pi \epsilon_o h}\left(\sin \frac{\pi}{2}-\sin \left(-\frac{\pi}{2}\right)\right) \\ & E^{\prime}=\frac{\lambda}{4 \pi \epsilon_o h} \times 2 \\ & E^{\prime}=\frac{\lambda}{2 \pi \epsilon_o h}\end{aligned}$
This is the net electric field due to a long wire with linear charge density λ at a distance h from it.
In the question, linear charge density =E
Therefore
$E'=\frac{E}{2\pi \epsilon_o h}$
Answer:
Given that a proton and a neutron consist of three quarks each.
And, ‘up’ quark is of charge + $\left ( \frac{2}{3} \right )$ e, and the ‘down’ quark of charge $\left (- \frac{1}{3} \right )$ e
Let the number of 'up' quarks be n. Therefore, the number of 'down' quarks is (3-n).
$\therefore$ The net charge = $\\ n\times\frac{2}{3}e + (3-n)\frac{-1}{3}e = (n-1)e$
Now, a proton has a charge +1e
$\therefore$ $(n-1)e = +1e \implies n =2$
Proton will have 2 u and 1 d, i.e, uud
Similarly, the neutron has a charge 0
$\therefore$ $(n-1)e = 0 \implies n =1$
Neutron will have 1 u and 2 d, i.e, udd
Answer:
For equilibrium to be stable, there must be a restoring force, and hence all the field lines should be directed inwards towards the null point. This implies that there is a net inward flux of the electric field. But this violates Gauss's law, which states that the flux of the electric field through a surface not enclosing any charge must be zero. Hence, the equilibrium of the test charge cannot be stable.
Therefore, the equilibrium is necessarily unstable.
Answer:
Two charges of the same magnitude and sign are placed at a certain distance apart. The mid-point of the line joining these charges will have E =0.
When a test charge is displaced along the line towards the charges, it experiences a restoring force(which is the condition for stable equilibrium). But if the test charge is displaced along the normal of the line, the net electrostatic force pushes it away from the starting point. Hence, the equilibrium is unstable.
Answer:
Let s be the vertical deflection, t be the time taken by the particle to travel between the plates
$\therefore$ $s = ut + \frac{1}{2}at^2$
Here, u =0, since initially there was no vertical component of velocity.
The particle in the electric field will experience a constant force (Since the electric field is constant).
F = ma = -qE (Using Newton's Second Law, F = ma)
$\therefore$ a = -qE/m (-ve sign implies here in downward direction)
Again, t = Distance covered/ Speed = $L/ v_{x}$
(In x-direction, since there is no force, the component of velocity in x-direction remains constant = $v_{x}$.
And, the distance covered in the x-direction = length of the plate = L)
Putting these values in our deflection equation,
$\\ s = ut + \frac{1}{2}at^2 = (0)(L/v_{x}) + \frac{1}{2}(-qE/m)(L/v_{x})^2 \\ \implies s =\frac{-qEL^2}{2mv_{x}^2}$
(S is -ve, which implies it deflects downwards.)
$\therefore$ The vertical deflection of the particle at the far edge of the plate is $\frac{qEL^{2}}{2mv_{x}^{2}}$.
This motion is similar to the motion of a projectile in a gravitational field, which is also a constant force. The force acting on the particle in the gravitational field is mg, while in this case, it is qE. The trajectory will be the same in both cases.
Answer:
$\therefore$ The vertical deflection of the particle at the far edge of the plate is $s=\frac{qEL^{2}}{2mv_{x}^{2}}$
given s= 0.5cm=0.005cm
Calculate L from the above equation
$L=\sqrt{\frac{2smv_x^2}{qE}}=\sqrt{\frac{2\times 0.005\times 9.1\times 10^{-31}(2\times10^6)^2 }{1.6\times 10^{-19}\times9.1\times10^2}}$
L=1.6 cm
Get your results instantly with our calculator!
Given below are Higher Order Thinking Skills (HOTS) questions from Class 12 Physics NCERT Chapter 1 to enhance conceptual understanding and problem-solving ability.
1. Two point charges $\mathrm{q}_1=3 \mu C$ and $\mathrm{q}_2=-4 \mu C$ are placed at points $(2 \hat{i}+3 \hat{j}+3 \hat{k})$ and $(\hat{i}+\hat{j}+\hat{k})$ respectively. Force on charge $q_2$ is $\_\_\_\_$ N. (Take $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9$ SI Units)
(A) $(12 \hat{i}+24 \hat{j}+24 \hat{k}) \times 10^{-3}$
(B) $(4 \hat{i}+8 \hat{j}+8 \hat{k}) \times 10^{-3}$
(C) $(3 \hat{i}+6 \hat{j}+6 \hat{k}) \times 10^{-3}$
(D) $(-4 \hat{i}-8 \hat{j}-8 \hat{k}) \times 10^{-3}$
Answer:
Coulomb's Law states that the force between two point charges is proportional to the product of the charges and inversely proportional to the square of the distance between them.
In vector form, the force $\vec{F}_{21}$ exerted on charge $q_2$ by charge $q_1$ is:
$
\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{|\overrightarrow{\mathrm{r}}|^2} \hat{\mathrm{r}}
$
Where,
$\vec{r}=\vec{r}_2-\vec{r}_1$ is the position vector from $q_1$ to $q_2, \hat{r}=\frac{\vec{r}}{|\vec{r}|}$ is the unit vector and $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9$
Substituting the unit vector, we get:
$
\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{|\overrightarrow{\mathrm{r}}|^3} \overrightarrow{\mathrm{r}}
$
Let $\vec{r}_1$ be the position of $q_1$ and $\vec{r}_2$ be the position of $q_2$ :
$
\begin{aligned}
& \overrightarrow{r_1}=2 \hat{\imath}+3 \hat{\jmath}+3 \hat{k} \\
& \overrightarrow{r_2}=1 \hat{\imath}+1 \hat{\jmath}+1 \hat{k}
\end{aligned}
$
The vector from $\mathrm{q}_1$ to $\mathrm{q}_2$ is :
$
\begin{aligned}
& \overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{r}}_2-\overrightarrow{\mathrm{r}}_1=(1-2) \hat{\mathrm{i}}+(1-3) \hat{\mathrm{j}}+(1-3) \hat{\mathrm{k}} \\
& \Rightarrow \overrightarrow{\mathrm{r}}=-\hat{\imath}-2 \hat{\jmath}-2 \hat{\mathrm{k}}
\end{aligned}
$
So, the magnitude of position vector is,
$
\begin{aligned}
& |\overrightarrow{\mathrm{r}}|=\sqrt{(-1)^2+(-2)^2+(-2)^2} \\
& \Rightarrow|\overrightarrow{\mathrm{r}}|=\sqrt{1+4+4}=\sqrt{9}=3 \mathrm{~m}
\end{aligned}
$
Substituting the values into the vector formula :
$
\begin{aligned}
& \vec{F}=\left(9 \times 10^9\right) \frac{\left(3 \times 10^{-6}\right)\left(-4 \times 10^{-6}\right)}{3^3}(-\hat{\imath}-2 \hat{\jmath}-2 \hat{k}) \\
& \Rightarrow \overrightarrow{\mathrm{F}}=\frac{9 \times 3 \times(-4) \times 10^{-3}}{27}(-\hat{\imath}-2 \hat{\jmath}-2 \hat{k}) \\
& \Rightarrow \vec{F}=\frac{-108 \times 10^{-3}}{27}(-\hat{\imath}-2 \hat{\jmath}-2 \hat{k}) \\
& \Rightarrow \overrightarrow{\mathrm{F}}=-4 \times 10^{-3}(-\hat{\imath}-2 \hat{\jmath}-2 \hat{\mathrm{k}}) \\
& \Rightarrow \overrightarrow{\mathrm{F}}=(4 \hat{\imath}+8 \hat{\jmath}+8 \hat{\mathrm{k}}) \times 10^{-3} \mathrm{~N}
\end{aligned}
$
Therefore, the force on charge $q_2$ is $(4 \hat{\imath}+8 \hat{\jmath}+8 \hat{k}) \times 10^{-3} \mathrm{~N}$.
Hence, the correct option is (B).
2.A rigid dipole undergoes a simple harmonic motion about its centre in the presence of an electric field $\overrightarrow{\mathrm{E}}_1=\mathrm{E}_0 \hat{x}$. If another electric field $\overrightarrow{\mathrm{E}}_2=2 \mathrm{E}_0(\hat{y}+\hat{z})$ is introduced to the system, what will be the percentage change in the frequency of the oscillation (approximate)?
A $73 \%$
B $63 \%$
C $83 \%$
D $53 \%$
Answer:
For small oscillations of an electric dipole,
$
\omega=\sqrt{\frac{p E}{I}} \quad \Rightarrow \quad f \propto \sqrt{E}
$
Case 1:
$
\begin{gathered}
E_1=E_0 \\
\omega_1=\sqrt{\frac{p E_0}{I}}
\end{gathered}
$
Case 2:
$
\begin{gathered}
\vec{E}_{\text {net }}=E_0 \hat{i}+2 E_0 \hat{j}+2 E_0 \hat{k} \\
E_{\text {net }}=\sqrt{E_0^2+\left(2 E_0\right)^2+\left(2 E_0\right)^2}=3 E_0 \\
\omega_2=\sqrt{\frac{p\left(3 E_0\right)}{I}}=\sqrt{3} \omega_1 \\
f_2=\sqrt{3} f_1
\end{gathered}
$
Percentage change in frequency:
$
\frac{f_2-f_1}{f_1} \times 100=(\sqrt{3}-1) \times 100 \approx 73 \%
$
3. Two point charges $8 \mu C$ and $-2 \mu C$ are located at $x=2 \mathrm{~cm}$ and $x=4 \mathrm{~cm}$, respectively on the $x$-axis. The ratio of electric flux due to these charges through two spheres of radii 3 cm and 5 cm with their centers at the origin is $\_\_\_\_$ .
A 4 : 1
B 3 : 4
C 4 :3
D $4: 5$
Answer:
For sphere with radius 3 cm and center origin
$
\phi_1=\frac{\mathrm{q}_{\mathrm{en}}}{\varepsilon_0}=\frac{8 \mu \mathrm{C}}{\varepsilon_0}
$
for sphere of radius 5 cm
$
\phi_2=\frac{\mathrm{q}_{\mathrm{en}}}{\varepsilon_0}=\frac{(8-2) \mu \mathrm{C}}{\varepsilon_0}=\frac{6 \mu \mathrm{C}}{\varepsilon_0}
$
4.Two charged conducting spheres $S_1$ and $S_2$ of radii 8 cm and 18 cm are connected to each other by a wire. After equilibrium is established, the ratio of electric fields on $S_1$ and $S_2$ spheres are $E_{S 1}$ and $E_{S 2}$ respectively. The value of $\frac{E_{S 1}}{E_{S 2}}$ is $\_\_\_\_$
(A) $\frac{3}{2}$
(B) $\frac{2}{3}$
(C) $\frac{4}{9}$
(D) $\frac{9}{4}$
$\begin{aligned} & \mathrm{V}_1=\mathrm{V}_2 \\ & \frac{\mathrm{kQ}_1}{8}=\frac{\mathrm{kQ}_2}{18} \quad\left\{\mathrm{v}_{\text {surface }}=\frac{\mathrm{kQ}}{\mathrm{R}}\right\} \\ & \frac{\mathrm{Q}_1}{\mathrm{Q}_2}=\frac{4}{9} \\ & \frac{\mathrm{E}_{\mathrm{S}_1}}{\mathrm{E}_{\mathrm{S}_2}}=\frac{\mathrm{kQ}_1}{\mathrm{r}_1^2} \frac{\mathrm{r}_2^2}{\mathrm{kQ}_2}\left\{\mathrm{E}_{\text {surface }}=\frac{\mathrm{kQ}}{\mathrm{R}^2}\right\} \\ & =\frac{\mathrm{Q}_1}{\mathrm{Q}_2}\left(\frac{\mathrm{r}_2}{\mathrm{r}_1}\right)^2=\frac{4}{9} \times\left(\frac{9}{4}\right)^2=\frac{9}{4}\end{aligned}$
5.Three charges $+2 q,+3 q$ and $-4 q$ are situated at $(0,-3 a),(2 a, 0)$ and $(-2 a, 0)$ respectively in the $x y$ plane. The resultant dipole moment about origin is $\_\_\_\_$ .
A $2 q a(7 \hat{i}-3 \hat{j})$
B $2 q a(3 \hat{j}-7 \hat{i})$
C $2 q a(3 \hat{i}-7 \hat{j})$
D $2 q a(3 \hat{j}-\hat{i})$
Answer:
$\begin{aligned} & \vec{p}=q_1 \vec{r}_1+q_2 \vec{r}_2+q_3 \vec{r}_3 \\ & \vec{p}=(2 q)(-3 a) \hat{j}+(3 q)(2 a) \hat{i} \\ & +(-4 q)(-2 a) \hat{i} \\ & \vec{p}=2 q a(7 \hat{i}-3 \hat{j})\end{aligned}$
Chapter 1 Electric Charges and Fields in Class 12 Physics introduces the fundamental concepts of electrostatics, focusing on how electric charges interact and create electric fields. This chapter lays the groundwork for understanding electric forces, Coulomb's law, and field lines.
1.1 Introduction
1.2 Electric Charge
1.3 Conductors and Insulators
1.4 Basic Properties of Electric Charge
1.4.1 Additivity of Charges
1.4.2 Charge Is Conserved
1.4.3 Quantisation of Charge
1.5 Coulomb’s Law
1.6 Forces Between Multiple Charges
1.7 Electric Field
1.7.1 Electric Field Due to a System of Charges
1.7.2 Physical Significance of Electric Field
1.8 Electric Field Lines
1.9 Electric Flux
1.10 Electric Dipole
1.10.1 The Field of an Electric Dipole
1.10.2 Physical Significance of Dipoles
1.11 Dipole in a Uniform External Field
1.12 Continuous Charge Distribution
1.13 Gauss’s Law
1.14 Applications of Gauss’s Law
1.14.1 Field Due to an Infinitely Long Straight Uniformly Charged Wire
1.14.2 Field Due to a Uniformly Charged Infinite Plane Sheet
1.14.3 Field Due to a Uniformly Charged Thin Spherical Shell
Electric Charges and Fields class 12 question answers: Important Formulas compile all the key equations and expressions from the chapter in one place, making revision quick and efficient. These formulas cover concepts like Coulomb's law, electric field intensity, electric potential, and Gauss's law, helping students solve problems with accuracy and speed.
1. Charge is a fundamental property of matter.
2. SI Unit: Coulomb (C)
3. Charge Quantization: $q=n e$ (where $n$ is an integer, $e=1.6 \times 10^{-19} \mathrm{C}$ )
The force between two point charges at a distance r is given by:
$
F=k \frac{\left|q_1 q_2\right|}{r^2}
$
where $k=\frac{1}{4 \pi f_0} \approx 9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2$
1. The electric field at a point due to an electric charge $q$ :
$
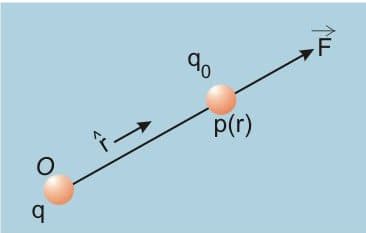
E=\frac{F}{q}=k \frac{q}{r^2}
$
2. For an electric Dipole at the Axial Position:
$
E=\frac{1}{4 \pi \varepsilon_0} \times \frac{2 p}{r^3}
$
3. For an electric Dipole at the Equatorial Position:
$
E=\frac{1}{4 \pi \varepsilon_0} \times \frac{p}{r^3}
$
1. Dipole Moment: $p=q \times d$
2. Torque on a Dipole in a Uniform Electric Field:
$
\tau=p E \sin \theta
$
1. Linear Charge Density $(\lambda): \lambda=\frac{q}{l}$
2. Surface Charge Density ( $\sigma$ ): $\sigma=\frac{q}{A}$
3. Volume Charge Density ( $\rho$ ): $\rho=\frac{q}{V}$
The total electric flux through a closed surface is:
$
\oint \mathbf{E} \cdot d \mathbf{A}=\frac{q}{\varepsilon_0}
$
1. Electric field due to an infinite line charge:
$
E=\frac{\lambda}{2 \pi \varepsilon_0 r}
$
2. Electric field due to a uniformly charged infinite plane:
$
E=\frac{\sigma}{2 \varepsilon_0}
$
3. Electric field due to a charged spherical shell:
Inside the shell: $E=0$
Outside the shell: $E=\frac{1}{4 \pi \varepsilon_0} \times \frac{q}{r^2}$
In order to answer the questions in Chapter 1 - Electric Charges and Fields of Physics Class 12, students should properly know the fundamentals of electrostatics and apply the formulas. This chapter contains both conceptual and numerical questions thus, the important part is to develop logical arguments and accuracy. Using a systematic approach is beneficial in addressing derivations, definitions and problem-based questions effectively when taking exams.
NCERT Solutions for Class 12 Physics Chapter 1 help students understand the fundamentals of electrostatics in a clear, structured, and exam-oriented way. The Electric Charges and Fields Class 12 NCERT Solutions make it easier to understand fundamental concepts, such as electric charge, Coulomb law, electric field, electric flux and Gauss law, which are the backbone of many physics problems. Dealing with definitions, derivations, and numerical problems one by one, Electric Charges and Fields NCERT Solutions simplify the visualisation and the application of such abstract concepts as field lines and flux. With frequent practice with these Electric Charges and Fields Class 12 Questions and Answers, confidence regarding solving derivations, field-based numericals and conceptual questions that are commonly given in CBSE board exams, JEE and NEET is developed. The accuracy and the speed of problem-solving are also enhanced with regular usage of the Electric Charges and Fields class 12 question answers, and the clarity of concepts becomes well-developed. Such focused preparation provides a solid background to the next chapters of electrostatics, like Electrostatic Potential and Capacitance, which provides a better understanding at a higher level, helps in achieving higher marks, and is helpful in the long term to remember the basics of physics.
NCERT Solutions for Class 12 Physics Chapter 1 Electric Charges and Fields are essential for understanding the fundamentals of electrostatics, which form the starting point of Class 12 Physics. The concepts presented in this chapter are very common in theoretical and numerical problems.
To score well in JEE and NEET, students must work beyond the NCERT syllabus with higher-level questions and be good at application-based concepts as well. The main differences in the additional preparation required to prepare for JEE and NEET are brought out in the table below.
NCERT Solutions for Class 12 Physics: Chapter-wise Links provide a structured pathway to access detailed solutions for every chapter in the syllabus. These NCERT Class 12 Physics Solutions help students understand concepts clearly, improve problem-solving skills, and prepare effectively for board exams and competitive tests.
NCERT Books and the NCERT Syllabus for Class 12 form the foundation of board exam preparation and competitive exam readiness. Easy access to these links helps students follow the latest curriculum, understand topic-wise weightage, and prepare systematically for CBSE board examinations.
NCERT Solutions subject-wise links provide easy access to chapter-wise answers for all major subjects in one place. These solutions help students understand concepts clearly, practise textbook questions effectively, and prepare confidently for exams
Frequently Asked Questions (FAQs)
Understanding electric charges and fields is fundamental to learning about electricity, electromagnetism, and how electric forces act at a distance—important for everything from electronics to physics research.
Electric charges are present in many daily phenomena, like static electricity, lightning, photocopiers, and electronic devices.
Many conceptual and numerical questions on Coulomb’s Law, electric field, and the superposition principle are frequently asked in NEET and JEE exams.
Yes, at certain points due to symmetry or superposition of fields, the net electric field can be zero.
The net charge inside a conductor is zero because charges redistribute on the surface. If the charge is zero then the electric field must be zero
NCERT Solutions breaks down difficult electrostatics problems into simple steps by offering detailed explanations for all in-text questions and exercises.
The chapter covers potential energy problems for charge systems, dipole moment calculations, electric field calculations at different distances, and Coulomb's law calculations for the force between point charges. Additionally, students apply Gauss's law for symmetric shapes, work with moving charges through electric fields, and solve problems involving fields caused by continuous charge distributions.
The NCERT Solutions offer step-by-step answers to all the in-text questions and exercises and reduce complex problems in electrostatics into small steps. The systematised problem-solving methods are necessary to calculate the electric fields and apply the law of Coulomb to develop conceptual clarity.
The solutions describe electric field lines as imaginary curves, the tangent of which at any point would provide the direction of the electric field, and line density would be the strength of the field. Field lines visualise the patterns of electric fields, which give students the patterns of fields surrounding various patterns of charges.
Thus, quantisation of charge states that electric charge is discrete and conserved, and it always exists in whole-number multiples of the elementary charge.
On Question asked by student community
Hello Dharani,
Check the link below to download NCERT Class 12 previous year question papers in PDF format for all subjects.
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers-class-12
Hello Vipin,
Check the link below to download CBSE Class 12 question papers in PDF format for all subjects, including Mathematics.
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers-class-12
Hello Shubham,
NCERT Class 12 Chemistry chapter-wise notes and solutions are available at the link given below. Keep checking for updated uploads when NCERT PYQs (Previous Year Questions) are published.
https://school.careers360.com/ncert/ncert-solutions-class-12-chemistry
Hi!
Given below is the link to access CBSE Class 12 Sociology Question Paper 2026 with Answer Key:
https://school.careers360.com/boards/cbse/cbse-class-12-sociology-answer-key-2026
Hello Hashi,
Download the CBSE Class 12 Business Studies 2026 paper from the link below to prepare effectively.
https://school.careers360.com/boards/cbse/cbse-class-12-business-studies-question-paper-2026
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Study at a world-renowned UK university in India | Admissions open for UG & PG programs.
Apply for UG & PG programmes from Victoria University, Delhi NCR Campus
Admissions open for UG & PG programs at Illinois Tech Mumbai
Apply for UG & PG courses at University of Aberdeen, Mumbai Campus
UG & PG Admissions open for CS/AI/Business/Economics & other programmes.
Bristol's expertise meets Mumbai's innovation. Admissions open for UG & PG programmes