Application of Derivatives Class 12th Notes - Free NCERT Class 12 Maths Chapter 6 Notes - Download PDF

NCERT Notes for Class 12 Chapter 6 Application of Derivatives: Free PDF Download

Students who wish to access the NCERT Notes for class 12, chapter 6, Application of Derivatives, can click on the link below to download the entire solution in PDF.

Download PDF

NCERT Notes for Class 12 Chapter 6: Application of Derivatives

Rate of change

For the function $y=f(x), \frac{d}{d x}(f(x))$ represents the rate of change of $y$ with respect to $x$. Thus, if ' $s$ ' represents the distance and ' $t$ ' the time, then $\frac{d s}{d t}$ represents the rate of change of distance with respect to time.

Derivative

Definition
The rate of change of distance (S) with respect to time (t) is called the rate of change.

Mathematical Representation: $\frac{d s}{d t}$

Mathematical Representation: $\frac{d y}{d x}=\frac{d y}{d t} \frac{d t}{d x}$ if $\frac{d x}{d t} \neq 0$

So, the rate of change of y with x can be calculated using the rate of change of y and x with respect to t.

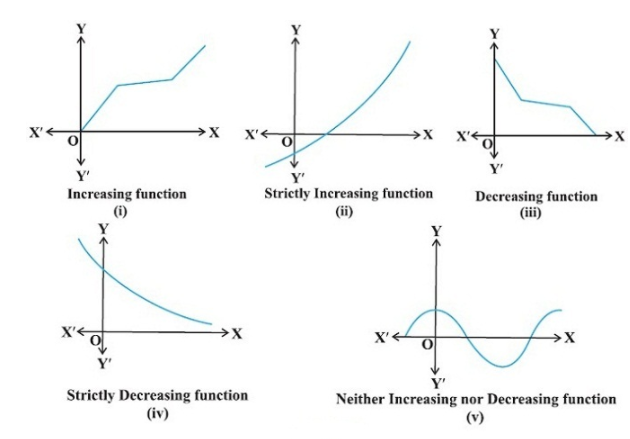
Increasing and Decreasing Functions

Definition

Strictly increasing: Function f: X→R is defined on an X⊂R is increasing if f(x) ≤ f(y) where x < y. If there is inequality that is strict, i.e., f(x)<f(y) where x<y, then f is strictly increasing.

Strictly decreasing: Function f: X→R is defined on an X⊂R is decreasing if f(x) ≥ f(y) where x < y. If there is inequality that is strict, i.e., f(x) > f(y) where x < y, then f is strictly decreasing.

Mathematical equations

a) Increasing if x₁ < x₂ ⇒ f (x₁) < f (x₂) for all x₁, x₂ ∈ (interval)

b) Decreasing if x₁ < x₂ ⇒f(x₁) < f(x₂) for all x₁, x₂ ∈ (interval)

c) If f(x) = c for all x ∈ intervals, where c is a constant.

d) Decreasing if x₁ < x₂ ⇒ f (x₁) ≥ f (x₂) for all x1, x₂ ∈ intervals.

e) Strictly decreasing if x₁ < x₂ ⇒ f(x₁) > f(x₂) for all x₁, x₂ ∈ interval

Theorem

Let f, which denotes a function, be a continuous function on [a, b] and be differentiable on the interval (a, b). Then

(a) f is said to be increasing in the interval [a, b] if f ′(x) > 0, where x ∈ (a, b)

(b) f is said to be decreasing in the interval [a, b] if f ′(x) < ,0 where x ∈ (a, b)

(c) f is said to be a constant function interval [a, b] if f ′(x) = 0 where x ∈ (a, b)

Proof
Let x₁, x₂ ∈ to interval [a, b] where x₁ < x₂. Then, by the Mean Value Theorem that is learned earlier:

$\begin{aligned} & f^{\prime}(c)=\frac{f(x_2)-f(x_1)}{(x_2-x_1)} \\ &\Rightarrow f(x_2)-f(x_1)=f^{\prime}(c)(x_2-x_1) \\ & \Rightarrow f(x_2)-f(x_1)>0\end{aligned}$

f(x₂) > f(x₁)

So x₁<x₂ in the interval (a, b).

Hence, f is said to be an increasing function in [a, b].

Similarly, it can be done to decrease functions as well. By simply interchanging the signs.

Graph for the Functions

Tangents and Normals

A line touching a curve $y=f(x)$ at a point $\left(x_1, y_1\right)$ is called the tangent to the curve at that point and its equation is given $y-y_1=\left(\frac{d y}{d x}\right)_{\left(x_1, y_1\right)}\left(x-x_1\right)$.
The normal to the curve is the line perpendicular to the tangent at the point of contact, and its equation is given as:
$y-y_1=\frac{-1}{\left(\frac{d y}{d x}\right)_{\left(x_1, y_1\right)}}\left(x-x_1\right)$

The angle of intersection between two curves is the angle between the tangents to the curves at the point of intersection.

Approximations

Since $f^{\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$, we can say that $f^{\prime}(x)$ is approximately equal to $\frac{f(x+\Delta x)-f(x)}{\Delta x}$
$\Rightarrow$ approximate value of $f(x+\Delta x)=f(x)+\Delta x \cdot f^{\prime}(x)$.

Increasing/decreasing functions

A continuous function in an interval $(a, b)$ is :
(i) strictly increasing if for all $x_1, x_2 \in(a, b), x_1<x_2 \Rightarrow f\left(x_1\right)<f\left(x_2\right)$ or for all $x \in(a, b), f^{\prime}(x)>0$

(ii) strictly decreasing if for all $x_1, x_2 \in(a, b), x_1<x_2 \Rightarrow f\left(x_1\right)>f\left(x_2\right)$ or for all $x \in(a, b), f^{\prime}(x)<0$

Theorem

Let $f$ be a continuous function on $[a, b]$ and differentiable in $(a, b)$,
then
(i) $f$ is increasing in $[a, b]$ if $f^{\prime}(x)>0$ for each $x \in(a, b)$
(ii) $f$ is decreasing in $[a, b]$ if $f^{\prime}(x)<0$ for each $x \in(a, b)$
(iii) $f$ is a constant function in $[a, b]$ if $f^{\prime}(x)=0$ for each $x \in(a, b)$.

Maxima and Minima

Local Maximum/Local Minimum for a real-valued function $f$
A point $c$ in the interior of the domain of $f$ is called
(i) a local maximum, if there exists an $h>0$, such that $f(c)>f(x)$, for all $x$ in $(c-h, c+h)$.

The value $f(c)$ is called the local maximum value of $f$.
(ii) local minima if there exists an $h>0$ such that $f(c)<f(x)$, for all $x$ in $(c-h, c+h)$.

The value $f(c)$ is called the local minimum value of $f$.
A function $f$ defined over $[a, b]$ is said to have maximum (or absolute maximum) at $x=c, c \in[a, b]$, if $f(x) \leq f(c)$ for all $x \in[a, b]$.

Similarly, a function $f(x)$ defined over $[a, b]$ is said to have a minimum [or absolute minimum $]$ at $x=d$ if $f(x) \geq f(d)$ for all $x \in[a, b]$.

Critical point of $f$: A point $c$ in the domain of a function $f$ at which either $f^{\prime}(c)=0$ or $f$ is not differentiable is called a critical point of $f$.

First Derivative Test

f is a function in the interval I, and f be continuous at point c in I, then

a) When f’(x) changes sign from positive to negative when x increases passing through c, that is, f’(x)>0 to the left of c and f’(x)<0 to the right of c, then c is called a point of maxima.

b) When f’(x) changes sign from negative to positive when x increases passing through c, that is f’(x)<0 to the left of c and f’(x)>0 to the right of c, then c is called a point of minima.

c) When f’(x) does not change when x increases, then c is neither a point of local maxima nor a point of local minima. It is called the point of inflexion.

Second Derivative Test

F is a function in the interval I, then f is twice differentiable (f’’(x)) at c, then

a) x=c, a point of local maxima only when f’(c) =0 and f’’(c) < 0 then f(C) is called local maximum of the function f.

b) x=c, a point of local minima only when f’(c) =0 and f’’(c) > 0 then f(C) is called a local minimum of the function f.

c) It doesn’t work if both f’(c)=0 and f’’(c)=0;

Absolute Maximum and Minimum Values

f is continuous in the interval I = [a, b]. f has both absolute

maximum and minimum values, and f has at least one value in the interval I;

Theorem

f be a continuous function in the interval I. f is a differentiable function in the Interval I. c be any point

a) f’(c) =0 if f gets its absolute maximum value at point c.

b) f’(c) =0 if f gets its absolute minimum value at point c.

We have a few working rules to find these values:

Step 1: Finding the critical points

Find f’(x) =0 or not differentiable;

Step 2: Take the extreme points in the interval.

Step 3: calculate all the values of f found above in steps 1,2;

Step 4: Find the maximum and minimum values that are found in Step 3. Among those maximum values, the greatest value of f will be the absolute maximum, and the least value will be the absolute minimum value of f.

Application of Derivatives: Previous Year Question and Answer

Question 1:
Find the values of ' $a$ ' for which $f(x)=\sqrt{3} \sin x-\cos x-2 a x+b$ is decreasing on $\mathbb{R}$.

Solution:
$f(x)=\sqrt{3} \sin x-\cos x-2 a x+b$

For $f(x)$ to be decreasing, $f'(x) \leq 0$ for all $x$.
$f'(x) = \sqrt{3} \cos x + \sin x - 2a$.
$\sqrt{3} \cos x + \sin x - 2a \leq 0$
$\sqrt{3} \cos x + \sin x \leq 2a$
The maximum value of $\sqrt{3} \cos x + \sin x$ is $\sqrt{(\sqrt{3})^2 + 1^2} = \sqrt{3+1} = 2$
For the inequality to hold for all $x$,
We need $2 \leq 2a$, which gives $a \geq 1$

Hence, the correct answer is ($a \geq 1$).

Question 2:
Find the intervals in which function $\mathrm{f}(x)=5 x^{\frac{3}{2}}-3 x^{\frac{5}{2}}$ is increasing.

Solution:
Given: $f(x) = 5x^{3/2} - 3x^{5/2}$

Differentiate with respect to x:
$f'(x) = \frac{15}{2}x^{1/2} - \frac{15}{2}x^{3/2} $

$= \frac{15}{2}\sqrt{x}(1-x)$
For increasing function, $f'(x) > 0$:
$\frac{15}{2}\sqrt{x}(1-x) > 0$
We have $\sqrt{x} > 0$, where $x>0$ and we need $1-x > 0$, which means $x < 1$.
Also, for $f(x)$ to be defined, $x \ge 0$.

At $x=0$, the derivative will be $0$, which means the function is neither decreasing nor increasing at this point, so we can not take $0$ in the interval where the function will be increasing.
Thus, the interval where $f(x)$ is increasing is $(0, 1)$.
Hence, the correct answer is $(0, 1)$.

Question 3:
The absolute maximum value of function $\mathrm{f}(x)=x^3-3 x+2$ in $[0,2]$ is:

Solution:
To find the absolute maximum of $f(x) = x^3 - 3x + 2$ in $[0, 2]$:

Differentiate both sides w.r.t. $x$,
$f'(x) = 3x^2 - 3$
Put the value of the derivative equal to zero,
$f'(x)= 0 $
$⇒3x^2 - 3=0$
$⇒3x^2=3$
$⇒x^2=1$
$\Rightarrow x = \pm 1$.
Only $x=1$ is the critical point in the interval.
Evaluate the value of $f(x)$ at critical point and endpoints:
$f(0) = 0^3 - 3(0) + 2 = 2$
$f(1) = 1^3 - 3(1) + 2 = 0$
$f(2) = 2^3 - 3(2) + 2 = 4$

The maximum value is $4$.

Hence, the correct answer is 4.

NCERT Class 12 Notes Chapter Wise:

Access all NCERT Class 12 Maths Notes from one place using the links below.

NCERT Exemplar Solutions Subject Wise

Access all the solutions of the NCERT Class 12 exemplar from one place using the links below.

• NCERT Exemplar Class 12 Solutions
• NCERT Exemplar Class 12 Maths
• NCERT Exemplar Class 12 Physics
• NCERT Exemplar Class 12 Chemistry
• NCERT Exemplar Class 12 Biology

NCERT Solutions Subject Wise

The links below allow students to access all the Maths solutions of various subjects from the NCERT book.

• NCERT Solutions for Class 12 Mathematics
• NCERT Solutions for Class 12 Chemistry
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for Class 12 Biology