Quadratic Equations Class 10th Notes - Free NCERT Class 10 Maths Chapter 4 Notes - Download PDF

Imagine after building your dream house, you need to fence that house, and for that, you need the length and breadth of that house to find the biggest possible area. Quadratic equations can solve this problem. It is an integral part of Mathematics that deals with algebraic equations of degree 2. People use quadratic equations in all parts of life to determine areas and moving object speeds, and make financial predictions while resolving problems throughout physics and engineering. The main purpose of these NCERT Notes of Quadratic Equations class 10 PDF is to provide students with an efficient study material from which they can revise the entire chapter.

After going through the textbook exercises and solutions, students need a type of study material from which they can recall concepts in a shorter time. Quadratic Equations Class 10 Notes are very useful in this regard. In this article about NCERT Class 10 Maths Notes, everything from definitions and properties to detailed notes, formulas, diagrams, and solved examples is fully covered by our subject matter experts at Careers360 to help the students understand the important concepts and feel confident about their studies. These NCERT Class 10 Maths Chapter 4 Notes are made in accordance with the latest CBSE syllabus while keeping it simple, well-structured and understandable. For the syllabus, solutions, and chapter-wise PDFs, head over to this link: NCERT.

Quadratic Equations Class 10 Notes: Free PDF Download

Use the link below to download the Quadratic Equations Class 10 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 10 Maths Chapter 4 Notes: Quadratic Equations

Quadratic Equations deal with equations of the form $a{x}^2+bx+c=0$. Students learn how to solve these equations using methods like factorisation, completing the square, and the quadratic formula. The chapter also explores the nature of roots using the discriminant.

Quadratic Polynomial

A polynomial with degree 2 is a quadratic polynomial. It is in the form of: f(x) = ax² + bx + c, where a ≠ 0.

Quadratic Equation

A quadratic polynomial, when equated to a constant (like 0), then the equation becomes a Quadratic Equation, which means f(x) = 0.

The standard form of a Quadratic Equation is: f(x) = ax² + bx + c = 0, where a, b and c are real numbers and a ≠ 0.
Here, a is called as quadratic coefficient, as it is the coefficient of x² and b is called as linear coefficient, as it is the coefficient of x, and c is the constant term.

Roots of a Quadratic Equation

A quadratic equation's roots represent x values that satisfy the given equation.
Let x = α, and α is a real number. If α satisfies the quadratic equation ax²+ bx + c = 0 such that aα² + bα + c = 0, then α is the root of the Quadratic Equation.

• As quadratic polynomials have degree two, quadratic equations can have two roots. Thus, the zeros of a quadratic polynomial f(x) = ax² + bx + c are the same as the roots of the quadratic equation ax² + bx + c = 0.
• Roots can be of three types, in case of a quadratic equation: two distinct roots, two equal roots or real roots may not exist.

Methods to Solve Quadratic Equations

There are three methods to solve Quadratic Equations.

1. Factorization Method

In this method, factorize the equation into two linear factors and equate each factor to zero to find the roots of the equation.

Step 1: Quadratic Equation in the form of ax² + bx + c = 0.

Step 2: Find the two numbers (let's say p and q), whose sum is equal to 'b' and product is equal to 'a × c'.

Step 3: By factorization, write ax² + bx + c = 0 as (x + p) (x + q) = 0

For example-

x²- 2x - 15=0

⇒ (x+3)(x-5)=0

So, x + 3 = 0 or, x - 5 = 0

$\therefore$ x = - 3 or x = 5

The above values of x are the two roots of the given quadratic equation.

2. Completing the Square Method

In this method, convert the equation to square form (x + a)² - b² = 0 or (x + a)² = b² to find the roots.

Example: Solve $x^2+6x+5=0$

Solution:

• Step 1: Make sure the coefficient of $x²$ is 1
  In this case, it's already 1.
  If not, divide the equation with the coefficient of $x²$.

• Step 2: Move the constant term to the right-hand side:
  $x^2+6x=-5$

• Step 3: Add the square of half the coefficient of $x$ to both sides:
  Half of 6 is 3, and $3^2=9$
  So, $x^2+6x+9=-5+9$

• Step 4: Write the left-hand side as a perfect square, to make the form (x + a)² = b²
  $(x+3{)}^2=4$

• Step 5: Take the square root of both sides:
  $x+3=\pm \sqrt{4}$

• Step 6: Solve for $x$:
  $x+3=\pm 2$
  $x=-3\pm 2$

Therefore, $x$ = -1 or -5

3. Quadratic formula method

In this method, find the roots by using the quadratic formula. The quadratic formula is

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

where a, b and c are the real numbers and b² – 4ac is known as the discriminant. In this method, we directly get the roots once we substitute the values in the formula.

Example: Solve $2x^2-4x-6=0$

Solution: Here, a = 2, b = -4, c = -6
Apply the quadratic formula: $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\frac{-(-4)\pm \sqrt{(-4{)}^2-4(2)(-6)}}{2(2)}$

$x=\frac{4\pm \sqrt{16+48}}{4}$

$x=\frac{4\pm \sqrt{64}}{4}$

$x=\frac{4\pm 8}{4}$

$x=\frac{4+8}{4}=3\text{or}x=\frac{4-8}{4}=-1$

$x=3\text{or}x=-1$

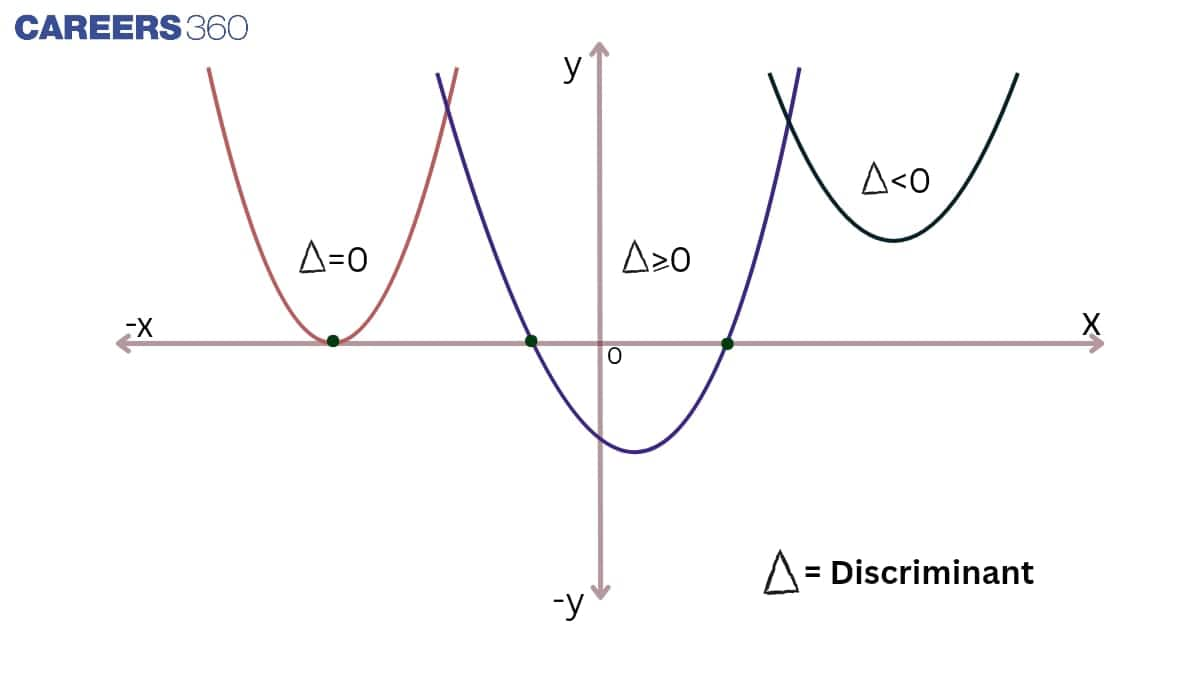
Nature of Roots

The nature of the roots of the equation depends upon the value of D, which is called the discriminant.

Solving using the quadratic formula when D > 0:

When the quadratic equation has D > 0, the roots of the equation are distinct and real.

Example: Solve $x^2-5x+6=0$

Solution: Here, a = 1, b = -5, c = 6

D = $(-5{)}^2-4(1)(6)$ = 25 - 24 = 1

It means D > 0.

Now, apply the quadratic formula:

x = $\frac{-(-5)\pm \sqrt{1}}{2(1)}=\frac{5\pm 1}{2}$

x = $3\text{or}x$ = 2

Therefore, the roots are distinct and real.

Solving using the quadratic formula when D = 0:

When the quadratic equation has D = 0, the roots of the equation are equal.

Example: Solve $x^2-4x+4=0$

Solution: Here, a = 1, b = -4, c = 4

D = $(-4{)}^2-4(1)(4)$= 16 - 16 = 0

It means D = 0.

Now, apply the quadratic formula:

x = $\frac{-(-4)}{2(1)}=\frac{4}{2}$ = 2

Therefore, x = 2

Thus, the roots are equal, as we get only one root.

Solving using the quadratic formula when D < 0:

When the quadratic equation has D < 0, the roots of the equation are not real (complex).

Example: Solve $x^2+2x+5=0$

Solution: Here, a = 1, b = 2, c = 5

D = $(2{)}^2-4(1)(5)$ = 4 - 20 = -16

It means D < 0.

Now, apply the quadratic formula:

x = $\frac{-2\pm \sqrt{-16}}{2(1)}=\frac{-2\pm 4i}{2}$

x = $-1\pm 2i$

Thus, the roots are not real and are complex numbers.

Quadratic Equations: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 10 chapter 4, Quadratic Equations:

Question 1: Find the nature of roots of the equation $4x^2-4a^{2}x+a^4-b^4=0$, $b\ne 0$

Solution:
Given, $4x^2-4a^{2}x+a^4-b^4=0,b\ne 0$

For the standard quadratic equation $A{x}^2+Bx+C=0$,

The sum of the roots is $-\frac{B}{A}$

The product of the roots is $\frac{C}{A}$

Discriminant $D=B^2-4AC\dots \dots (1)$

where $B=-4a^2,A=4,C=a^4-b^4$

Substitute the above-mentioned values in equation (1)

$D=(-4a^2{)}^2-4\times 4\times (a^4-b^4)$

$D=16b^4\Rightarrow D>0$

$\therefore$ The equation has real and distinct roots.

Question 2: Solve the quadratic equation $\sqrt{3}{x}^2+10x+7\sqrt{3}=0$ using quadratic formula.

Solution:
$\begin{array}{rl}& \sqrt{3}{x}^2+10x+7\sqrt{3}=0\\ & \Rightarrow \sqrt{3}{x}^2+3x+7x+7\sqrt{3}=0\\ & \Rightarrow \sqrt{3}x(x+\sqrt{3})+7(x+\sqrt{3})=0\\ & \Rightarrow \sqrt{3}x+7=0\text{ or }\mathrm{x}+\sqrt{3}=0\end{array}$
$\Rightarrow x=-\frac{7}{\sqrt{3}}$ or $-\sqrt{3}$.
There are two roots of the equation.
Hence, the answer is ($-\frac{7}{\sqrt{3}},-\sqrt{3}$).

Question 3: The sum of a number and its reciprocal is $\frac{13}{6}$. Find the number.

Solution:
Let the number be $x$.
$x+\frac{1}{x}=\frac{13}{6}$
$\Rightarrow \frac{x^2+1}{x}=\frac{13}{6}$
$\Rightarrow 6\times (x^2+1)=13x$
$\Rightarrow 6x^2+6-13x=0$
$\Rightarrow 6x^2-9x-4x+6=0$
$\Rightarrow 3x(2x-3)-2(2x-3)=0$
$\Rightarrow x=\frac{2}{3}$ or $x=\frac{3}{2}$
Hence, the answer is ($\frac{2}{3}$ or $\frac{3}{2}$).

Class 10 Chapter Wise Notes

All the links to chapter-wise notes for NCERT class 10 maths are given below:

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10
• NCERT Syllabus for Class 10