Triangles Class 10th Notes - Free NCERT Class 10 Maths Chapter 6 Notes - Download PDF

Geometry relies on triangles as one of its fundamental elements because they serve as foundations for multiple mathematical definitions, along with practical industrial uses. A triangle represents a fundamental closed polygon having three sides together with three angles, while also having three vertices, which have crucial significance in mathematics. This section discusses triangle classifications along with the Pythagoras theorem and the Basic Proportionality theorem, and describes the applications of triangle similarity in direct measurement calculations. The main purpose of these NCERT Notes of Triangles class 10 PDF is to provide students with an efficient study material from which they can revise the entire chapter.

After going through the textbook exercises and solutions, students need a type of study material from which they can recall concepts in a shorter time. Triangles Class 10 Notes are very useful in this regard. In this article about NCERT Class 10 Maths Notes, everything from definitions and properties to detailed notes, formulas, diagrams, and solved examples is fully covered by our subject matter experts at Careers360 to help the students understand the important concepts and feel confident about their studies. These NCERT Class 10 Maths Chapter 6 Notes are made in accordance with the latest CBSE syllabus while keeping it simple, well-structured and understandable. For the syllabus, solutions, and chapter-wise PDFs, head over to this link: NCERT.

Triangles Class 10 Notes: Free PDF Download

Use the link below to download the Triangles Class 10 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 10 Maths Chapter 6 Notes: Triangles

A triangle exists as a polygon closed by three sides, three angles, and three vertices. Every triangle contains interior angle measures that total up to 180 degrees, and exterior angles total up to 360 degrees.

Types of Triangles:

Triangles can be classified based on sides and angles:

Based on Sides:

There are different triangle types which depend on the length measurements of their sides. The classification system helps both understand properties and solve related problems more easily. Based on the sides triangle is divided into three types:

• Scalene Triangle: No sides are equal.

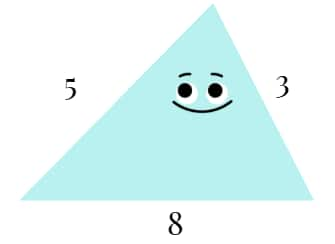
• Isosceles Triangle: Two sides are equal.

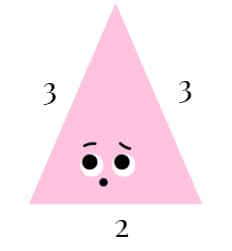
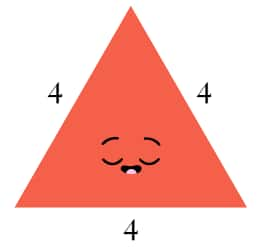
• Equilateral Triangle: All three sides are equal.

Based on Angles:

Relating to angles forms an additional way to categorize triangles. The classification of triangle shapes allows a better understanding of angle characteristics while solving geometric problems. On the basis of angles triangle is divided into 3 types:

• Acute Triangle: All angles are less than 90°

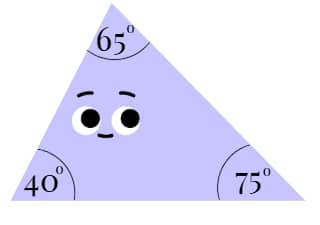
• Right Triangle: One angle is exactly 90°

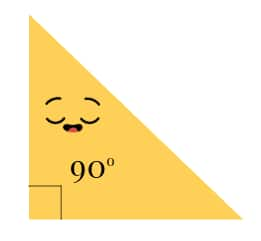
• Obtuse Triangle: One angle is greater than 90°

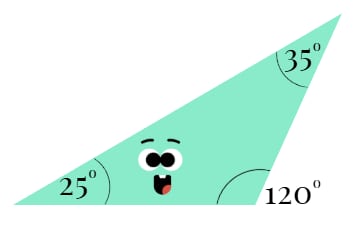
Similarity of Polygons:

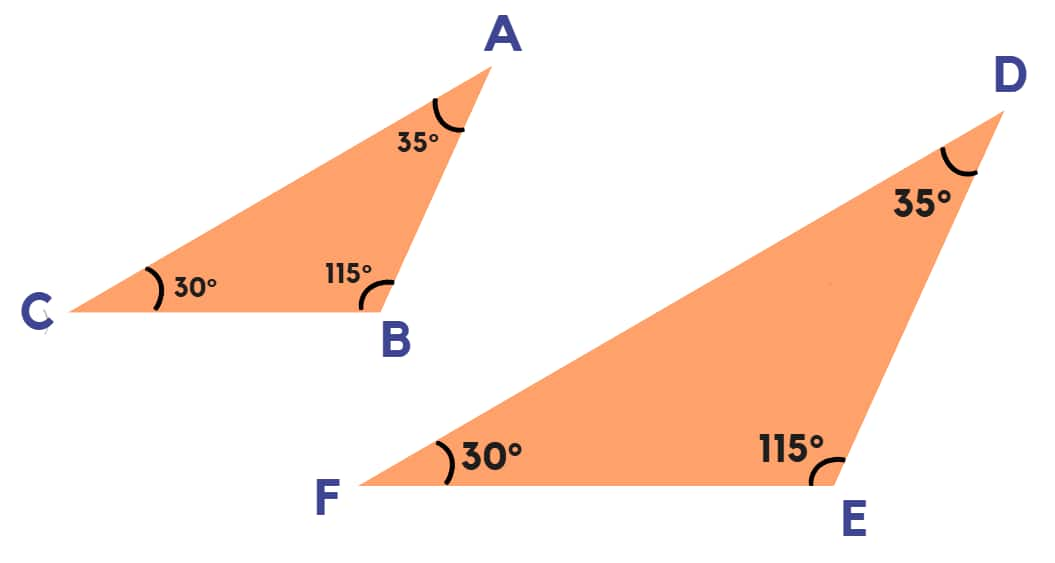
In geometry, two shapes qualify as similar if they share equivalent shapes regardless of dimensional differences. In the case of polygons, two polygons are said to be similar if:

• Their corresponding angles are equal.
• The ratios between corresponding triangle sides remain equal.

Therefore, this means that if two triangles are given ∆ABC and ∆DEF, they are said to be similar if:

1) ∠A =∠D, ∠B =∠E and ∠C =∠F

As like:-

OR

2) $\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}$

As like:-

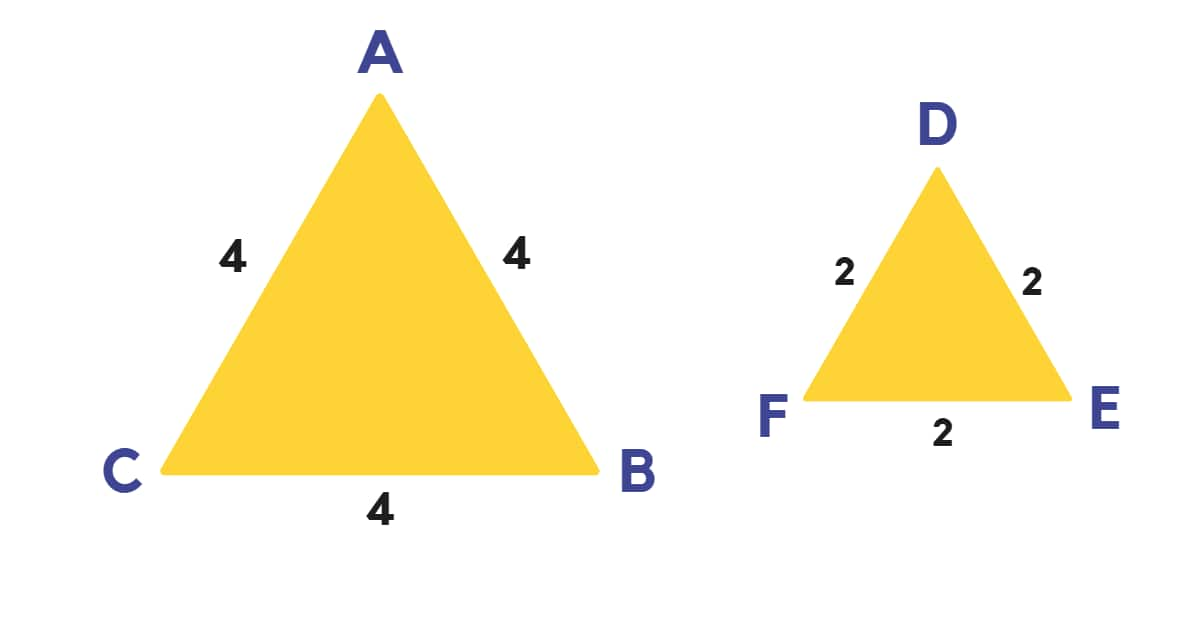
Difference Between Congruent and Similar Figures:

• Congruent Figures:

Two or more triangles are congruent if they have the same size and shape. Congruence is denoted by the symbol "≅" and read as "is congruent to". The shapes perfectly fit together when placed on top of each other. Congruent triangles can be flipped, rotated and mirrored and will still be congruent. Example: Two copies of the same triangle.

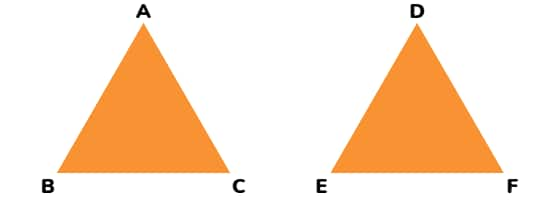
△ABC ≅ △DEF

• Similar Figures:

Two similar figures have the same shape but not necessarily the same size. One figure may exist at a different scale than the other while retaining the same basic dimensions. Similarity is denoted by the sign “~”. Example: A small triangle inside a bigger triangle with the same angles but different side lengths.

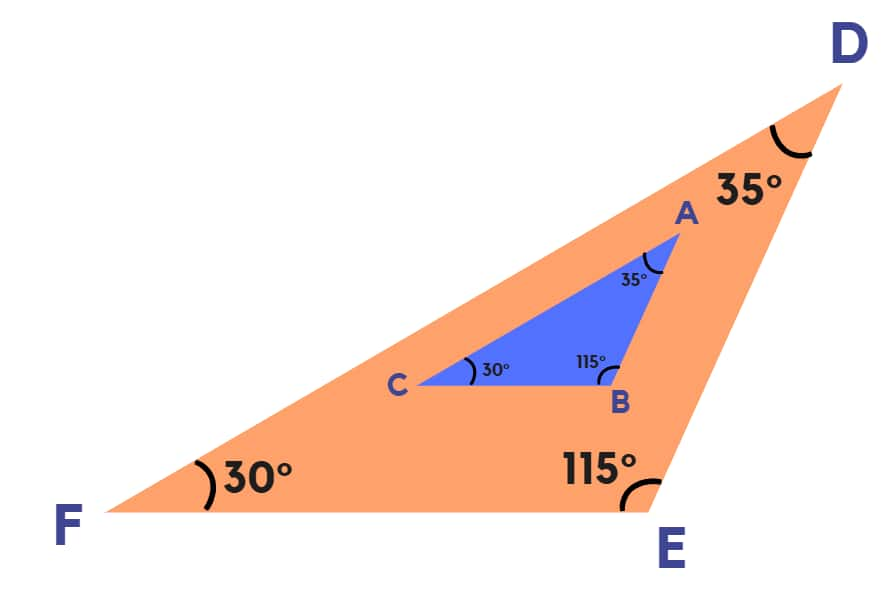
△ABC ~ △DEF

Observation:

From the above, we can say that:

• All congruent figures are similar.
• Similar figures need not be congruent.

Conditions for Similarity of Triangles:

To check whether two triangles are similar, there are three conditions:

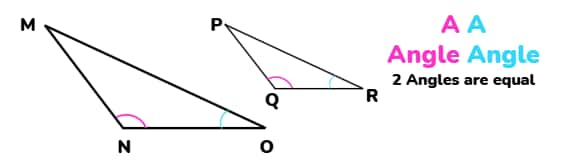
1. AA (Angle-Angle) Similarity Criterion:

If two triangles have their corresponding two angles equal, then the triangles are said to be similar triangles. This happens because when two angles match, the third angle will automatically match. After all, every triangle features a 180° angle total.

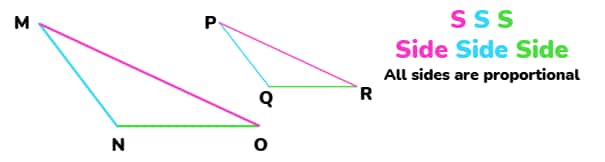
2. SSS (Side-Side-Side) Similarity Criterion:

Two triangles are similar when their corresponding sides maintain the same ratio because this proportionality results in equal corresponding angles. Example: If in one triangle, the sides are 3 cm, 6 cm, and 9 cm, and in another triangle, the sides are 6 cm, 12 cm, and 18 cm, then the ratio is the same (1:2), so they are similar.

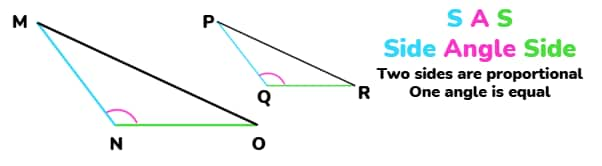
3. SAS (Side-Angle-Side) Similarity Criterion:

Two triangles are similar when they share equal angles between corresponding sides, which also stand in an equal proportional relation. Example: If one triangle has sides 5 cm and 10 cm with an included angle of 50°, and another triangle has sides 10 cm and 20 cm with an included angle of 50°, they are similar.

Theorems on Similarity of Triangles:

Basic Proportionality Theorem (Thales’ Theorem)

The Basic Proportionality Theorem (BPT), also known as Thales’ Theorem, states that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Mathematical Representation:

Consider ΔABC, where DE is a line parallel to BC, and it cuts AB at D and AC at E. Then, according to the theorem:

$\frac{AD}{DB}=\frac{AE}{EC}$

Proof:

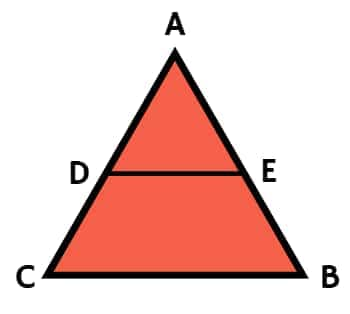
1. Since DE is parallel to BC, ∠ADE = ∠ABC and ∠DEA = ∠BCA (corresponding angles).
2. By AA similarity, ΔADE is similar to ΔABC.
3. As a result of similarity,
   $\frac{AD}{DB}=\frac{AE}{EC}$

Pythagoras Theorem:

As per Pythagoras' Theorem, “In a right-angled triangle, the sum of squares of two sides of a right triangle is equal to the square of the hypotenuse of the triangle.”

This means:

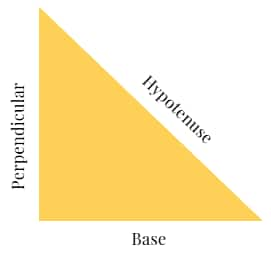
(Hypotenuse)² = (Base)² + (Perpendicular)²

Area of Similar Triangles:

When the two similar triangles are given, then the square of the ratio of their corresponding sides will be equal to the ratio of their area.

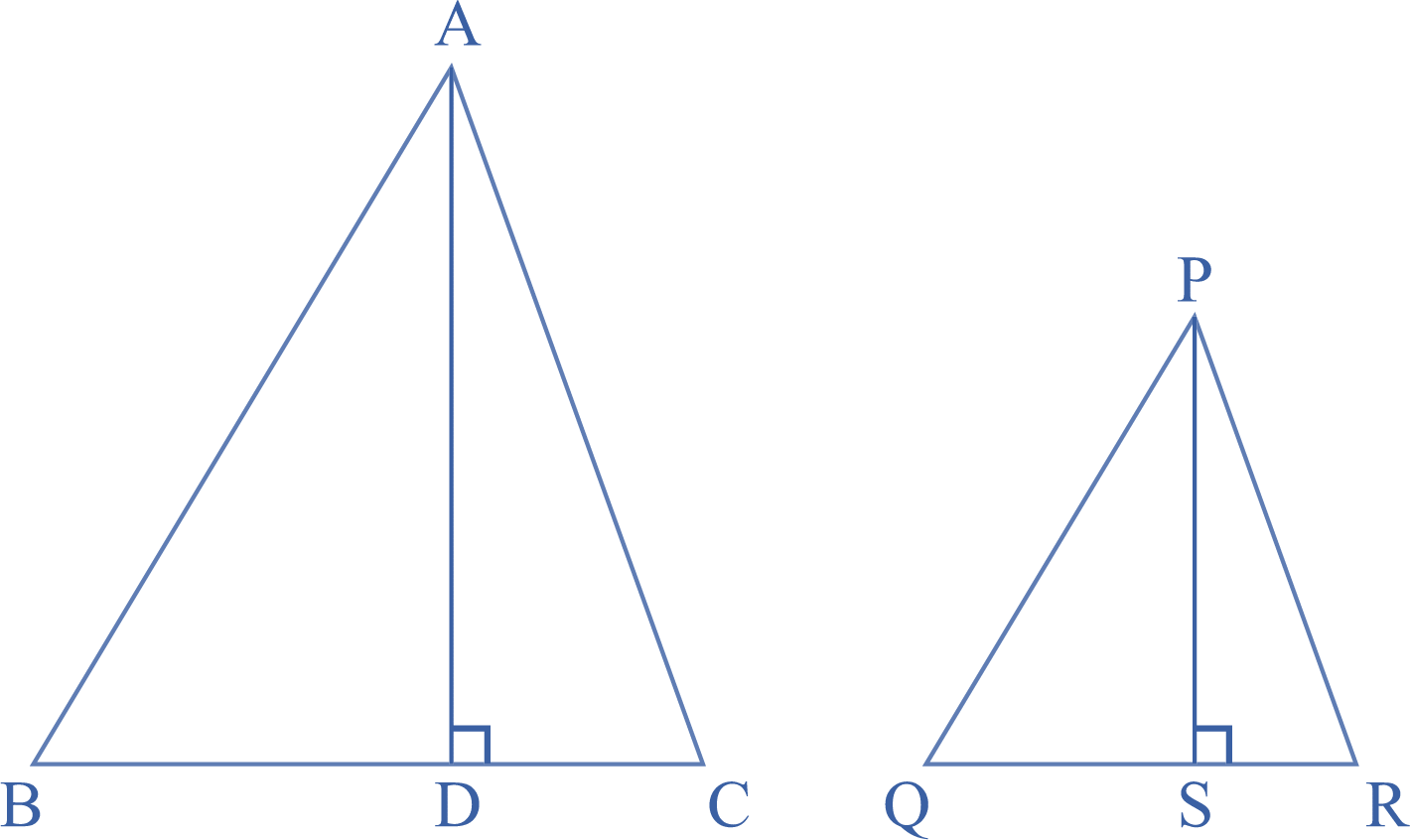
If ∆ABC ~ ∆PQR, then

$\frac{ar(ABC)}{ar(PQR)}={\frac{AB}{PQ}}^2={\frac{BC}{QR}}^2={\frac{AC}{PR}}^2$

Triangles: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 10 chapter 6, Triangles:

Question 1: The perimeters of two similar triangles are 22 cm and 33 cm, respectively. If one side of the first triangle is 9 cm, then find the length of the corresponding side of the second triangle.

Solution:
Let $x$ be the length of the corresponding side of the second triangle.
Ratio of perimeters of similar triangles = Ratio of corresponding sides.
$\frac{22}{33}=\frac{9}{x}$
$\Rightarrow \frac{2}{3}=\frac{9}{x}$
$\Rightarrow 2x=3\times 9$
$\Rightarrow 2x=27$
$\Rightarrow x=\frac{27}{2}=13.5$ cm.
Hence, the answer is $13.5$ cm.

Question 2: In $\mathrm{△}\mathrm{ABC},\mathrm{DE}\Vert \mathrm{BC}$. If $\mathrm{AE}=(2x+1)\mathrm{cm},\mathrm{EC}=4\mathrm{cm},\mathrm{AD}=(x+1)\mathrm{cm}$ and DB $=3\mathrm{cm}$, then value of $x$ is

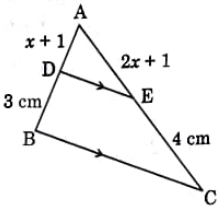
Solution:

$\mathrm{△}ABC$, with $DE\Vert BC$

$AE=(2x+1)\mathrm{cm}$

$EC=4\mathrm{cm}$

$AD=(x+1)\mathrm{cm}$

$DB=3\mathrm{cm}$

Basic Proportionality Theorem: If a line is drawn parallel to one side of a triangle and intersects the other two sides, then it divides those two sides in the same ratio.

By Basic Proportionality Theorem:

$\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}$

Substitute the given values:

$\frac{x+1}{3}=\frac{2x+1}{4}$

$\Rightarrow 4(x+1)=3(2x+1)$

$\Rightarrow 4x+4=6x+3$

$\Rightarrow 4-3=6x-4x$

$\Rightarrow 1=2x$

$\Rightarrow x=\frac{1}{2}$

Hence, the correct answer is $\frac{1}{2}$.

Question 3:
Assertion (A): $\mathrm{△}\mathrm{ABC}\sim \mathrm{△}\mathrm{PQR}$ such that $\mathrm{\angle }\mathrm{A}={65}^{\circ },\mathrm{\angle }\mathrm{C}={60}^{\circ }$. Hence $\mathrm{\angle }Q={55}^{\circ }$.
Reason (R): The Sum of all angles of a triangle is ${180}^{\circ }$.

Option (1): Both Assertion (A) and Reason (R) are true and Reason (R) is correct explanation of Assertion (A).
Option (2): Both Assertion (A) and Reason (R) are true, but Reason (R) is not correct explanation for Assertion (A).
Option (3): Assertion (A) is true, but Reason (R) is false.
Option (4): Assertion (A) is false, but Reason (R) is true.

Solution:
It is known that the sum of all angles of a triangle is ${180}^{\circ }$

So, Reason (R) is true (sum of angles in a triangle is ${180}^{\circ }$).

Since $\mathrm{△}ABC\sim \mathrm{△}PQR$, their corresponding angles are equal.

Given: $\mathrm{\angle }A={65}^{\circ },\mathrm{\angle }C={60}^{\circ }$

Let's find $\mathrm{\angle }B$ using triangle angle sum:

$\mathrm{\angle }B={180}^{\circ }-({65}^{\circ }+{60}^{\circ })={55}^{\circ }$

So, in the similar triangle $\mathrm{△}PQR$ :
$\mathrm{\angle }A=\mathrm{\angle }P={65}^{\circ }$
$\mathrm{\angle }B=\mathrm{\angle }Q={55}^{\circ }$
$\mathrm{\angle }C=\mathrm{\angle }R={60}^{\circ }$

So, the assertion is also TRUE.

Hence, the correct answer is option (1).

Class 10 Chapter Wise Notes

All the links to chapter-wise notes for NCERT class 10 maths are given below:

NCERT Exemplar Solutions for Class 10

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10
• NCERT Syllabus for Class 10