• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 - Areas related to circles

Edited By Ramraj Saini | Updated on Nov 27, 2023 05:14 PM IST

NCERT Solutions For Class 10 Maths Chapter 12 Exercise 12.3

NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 Areas related to circles are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 12.3 introduces areas and perimeters of plane figures like square, rectangle, parallelogram etc. Previously we have calculated the areas of figures separately like circle, square, prism, pyramid etc. This ex 12.3 class 10 also includes the combination of figures. We find the combination of plane figures use in our daily life and in the form of various interesting designs. The concepts related to areas figures and their combinations are well explained in this NCERT book Class 10 Maths chapter 12 exercise 12.3

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 12 Exercise 12.3
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 12 exercise 12.3
  3. Assess NCERT Solutions for Class 10 Maths chapter 12 exercise 12.3
  4. More About NCERT Solutions for Class 10 Maths Exercise 12.3
  5. Benefits of NCERT Solutions for Class 10 Maths Exercise 12.3
  6. NCERT Solutions for Class 10 Subject Wise
NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 - Areas related to circles
NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 - Areas related to circles

In this class 10 ex 12.3, we have interesting designs like a flower bed, drain cover, window designs are such examples. 10th class Maths exercise 12.3 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 12 exercise 12.3

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 12 exercise 12.3

Areas Related to Circles Class 10 Chapter 12 Exercise: 12.3

Q1 Find the area of the shaded region in Fig, if PQ = 24 cm, PR = 7 cm, and O is the center of the circle.

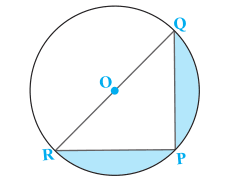1640759588049 Answer:

We know that \angle RPQ is 90 o as ROQ is the diameter.

RQ can be found using the Pythagoras theorem.

RP^2\ +\ PQ^2\ =\ QR^2

or 7^2\ +\ 24^2\ =\ QR^2

or QR\ =\ \sqrt{625}\ =\ 25\ cm

Now, the area of the shaded region is given by = Area of semicircle - Area of \Delta PQR

The area of a semicircle is:-

=\ \frac{1}{2}\pi r^2

or =\ \frac{1}{2}\pi \times \left ( \frac{25}{2} \right )^2

or =\ 245.53\ cm^2

And, the area of triangle PQR is :

=\ \frac{1}{2}\times 24\times 7\ =\ 84\ cm^2

Hence the area of the shaded region is : =\ 245.53\ -\ 84\ =\ 161.53\ cm^2

Q2 Find the area of the shaded region in Fig, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and \angle AOC = 40\degree .

Answer:

The area of a shaded region can be easily found by using the formula of the area of the sector.

Area of the shaded region is given by : Area of sector OAFC - Area of sector OBED

=\ \frac{40^{\circ}}{360^{\circ}}\times \pi (14)^2\ -\ \frac{40^{\circ}}{360^{\circ}}\times \pi (7)^2

=\ \frac{616}{9}\ -\ \frac{154}{9}\ =\ \frac{462}{9}

=\ 51.33\ cm^2

Q3 Find the area of the shaded region in Fig, if ABCD is a square of side 14 cm and APD and BPC are semicircles.

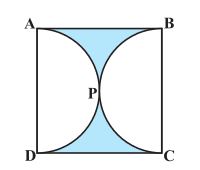1656402618695 Answer:

Area of the shaded region is given by = Area of the square - Area of two semicircles.

Area of square is : =\ 14^2\ =\ 196\ cm^2

And the area of the semicircle is:-

=\ \frac{1}{2}\pi r^2

=\ \frac{1}{2}\pi \times 7^2

=\ 77\ cm^2

Hence the area of the shaded region is given by : =\ 196 - 2(77) = 42\ cm^2.

Q4 Find the area of the shaded region in Fig, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as the centre.

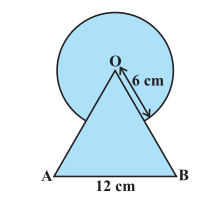
1656402667271

Answer:

Area of the shaded region is given by = Area of triangle + Area of the circle - Area of the sector

Area of the sector is : -

=\ \frac{60^{\circ}}{360^{\circ}}\times \pi\times 6^2

or =\ \frac{132}{7}\ cm^2

And, the area of the triangle is :

=\ \frac{\sqrt{3}}{4}a^2\ =\ \frac{\sqrt{3}}{4}\times 12^2\ =\ 36\sqrt{3}\ cm^2

And, the area of the circle is : =\ \pi r^2

or =\ \pi \times 6^2

or =\ \frac{792}{7}\ cm^2

Hence the area of the shaded region is:-

=\ 36\sqrt{3}\ +\ \frac{792}{7}\ -\ \frac{132}{7}

or =\ \left ( 36\sqrt{3}\ +\ \frac{660}{7} \right )\ cm^2

Q5 From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. Find the area of the remaining portion of the square.

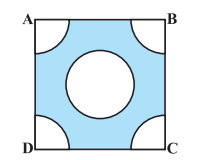
1656402791843

Answer:

Consider the quadrant in the given figure:- We have an angle of the sector as 90 o and radius 1 cm.

Thus the area of the quadrant is:-

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi\times 1^2

or =\ \frac{22}{28}\ cm^2

And the area of the square is : =\ side^2

=\ 4^2

=\ 16\ cm^2

And, the area of the circle is:-

=\ \pi r^2\ =\ \pi \times 1^2\ =\ \pi\ cm^2

Hence the area of the shaded region is: = Area of the square - Area of the circle - 4 (Area of quadrant)

or =\ 16\ -\ \frac{22}{7}\ -\ 4\left ( \frac{22}{28} \right )

or =\ \frac{68}{7}\ cm^2

Q6 In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. Find the area of the design.

Answer:

Assume the center of the circle to be point C and AD as the median of the equilateral triangle.

Then we can write:-

AO\ =\ \frac{2}{3}AD

or 32\ =\ \frac{2}{3}AD

Thus AD\ =\ 48\ cm

Consider \Delta ABD,

AB^2\ =\ AD^2\ +\ BD^2

or AB^2\ =\ 48^2\ +\ \left ( \frac{AB}{2} \right )^2

or AB\ =\ 32\sqrt{3}\ cm

Thus the area of an equilateral triangle is:-

=\ \frac{\sqrt{3}}{4}\times \left ( 32\sqrt{3} \right )^2

or =\ 768\sqrt{3}\ cm^2

And the area of the circle is : =\ \pi r^2\ =\ \pi\times 32^2

or =\ \frac{22528}{7} cm^2

Hence the area of the design is:-

=\ \left ( \frac{22528}{7}\ -\ 768 \sqrt{3} \right )\ cm^2

Q7. In Fig, ABCD is a square of side 14 cm. With centers A, B, C, and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.

Answer:

It is clear from the figure that the area of all sectors is equal (due to symmetry).

Also, the angle of the sector is 90 o and the radius is 7 cm.

Thus the area of the sector is:-

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi (7)^2

or =\ \frac{77}{2}\ cm^2

And, the area of the square is : =\ a^2\ =\ 14^2\ =\ 196\ cm^2

Hence the area of the shaded region is :

=\ 196\ -\ 4\times \frac{77}{2}

=\ 42\ cm^2

Q8 Fig. depicts a racing track whose left and right ends are semicircular.

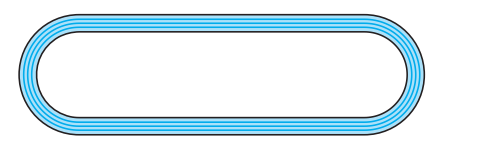
1636091567493

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :

(i) the distance around the track along its inner edge

Answer:

The distance around the track is Length of two straight lines + Length of two arcs.

Length of the arc is -

=\ \frac{1}{2}\times 2\pi r

=\ \frac{1}{2}\times 2\pi \times 30\ =\ 30\pi\ m

Thus the length of the inner track is :

=\ 106\ +\ 30\pi\ +\ 106\ +\ 30\pi

=\ 212\ +\ 60\pi

=\ \frac{2804}{7}\ m

Q8 Fig. depicts a racing track whose left and right ends are semicircular.

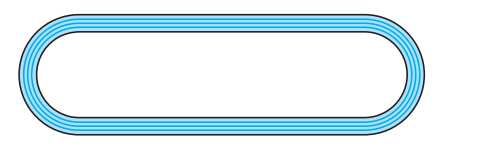
1636091587830

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :

(ii) the area of the track.

Answer:

The area of track = Area of outer structure - Area of inner structure.

Area of outer structure is: = Area of square + Area of 2 semicircles

=\ 106\times 80\ +\ \frac{1}{2}\pi (40)^2\ +\ \frac{1}{2}\pi (40)^2\ m^2

And, area of inner structure: = Area of inner square + Area of 2 inner semicircles

=\ 106\times 60\ +\ \frac{1}{2}\pi (30)^2\ +\ \frac{1}{2}\pi (30)^2\ m^2

Thus the area of the track is :

\\=\ 106\times 80\ +\ \frac{1}{2}\pi (40)^2\ +\ \frac{1}{2}\pi (40)^2\ -\ \left ( 106\times 60\ +\ \frac{1}{2}\pi (30)^2\ +\ \frac{1}{2}\pi (30)^2 \right )\\\\=\ 4320\ m^2

Hence the area of the track is 4320 m 2 .

Q9 In Fig, AB, and CD are two diameters of a circle (with center O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

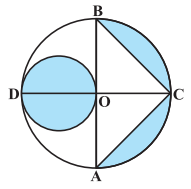
1636091578284

Answer:

Firstly, the area of the smaller circle is :

=\ \pi r^2

=\ \pi \times \left ( \frac{7}{2} \right )^2

=\ \frac{77}{2}\ cm^2

Now, the area of \Delta ABC :-

=\ \frac{1}{2}\times AB\times OC

or =\ \frac{1}{2}\times 14\times 7\ =\ 49\ cm^2

And, the area of the bigger semicircle is :

=\ \frac{1}{2}\pi r^2

=\ \frac{1}{2}\pi \times 7^2

=\ 77\ cm^2

Hence the area of the shaded region is:-

=\ \frac{77}{2}\ +\ 77\ -\ 49

=\ 66.5\ cm^2

Therefore the area of the shaded region is 66.5 cm 2 .

Q10 The area of an equilateral triangle ABC is 17320.5 cm 2 . With each vertex of the triangle as the centre, a circle is drawn with a radius equal to half the length of the side of the triangle (see Fig.). Find the area of the shaded region. (Use \pi = 3.14 and \sqrt3 = 1.73205 )

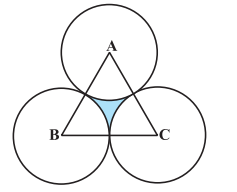
1636091615101

Answer:

Area of an equilateral triangle is:-

=\ \frac{\sqrt{3}}{4}\times a^2

\frac{\sqrt{3}}{4}\times a^2\ =\ 17320.5

a\ =\ 200\ cm

Now, consider the sector:- Angle of the sector is 60 o and the radius is 100 cm.

Thus the area of the sector:-

=\ \frac{60^{\circ}}{360^{\circ}}\times \pi \times 100^2

=\ \frac{15700}{3}\ cm^2

Thus the area of the shaded region is :

=\ 17320.5\ -\ 3\times \frac{15700}{3}

=\ 1620.5\ cm^2

Q11 On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig.). Find the area of the remaining portion of the handkerchief.

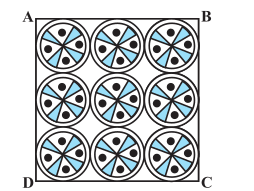
1636091628689

Answer:

Since one side of the square has 3 circles, thus the side of the square is 42 cm.

Area of the square : =\ a^2\ =\ 42^2\ =\ 1764\ cm^2

And, area of a circle :

=\ \pi r^2\ =\ \frac{22}{7}\times 7^2

=\ 154\ cm^2

Hence the area of the remaining portion is : =\ 1764\ -\ 9\times 154

=\ 378\ cm^2

Q12 In Fig, OACB is a quadrant of a circle with center O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB

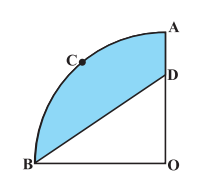
1636091641153

Answer:

The quadrant OACB is a sector with angle 90 o and radius 3.5 cm.

Thus the area of the quadrant is:-

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 3.5^2

=\ \frac{77}{8}\ cm^2

Hence the area of the quadrant is \frac{77}{8}\ cm^2 .

Q12 In Fig, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (ii) shaded region.

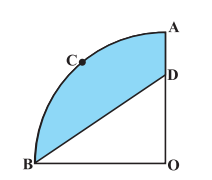
1636091648074

Answer:

For area of shaded region we need to find area of the triangle.

Area of triangle is:-

=\ \frac{1}{2}\times 3.5\times 2

=\ 3.5\ cm^2

Hence the area of the shaded region is = Area of the quadrant - Area of triangle

=\ \frac{77}{8}\ -\ 3.5

=\ \frac{49}{8}\ cm^2

Q13 In Fig, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use \pi = 3.14 )

1636091662355

Answer:

In the given figure we need to find the radius of the circle:-

Consider \Delta OAB,

OB^2\ =\ OA^2\ +\ AB^2

=\ 20^2\ +\ 20^2

OB\ =\ 20\sqrt{2}\ cm

Thus area of quadrant:-

=\ \frac{90^{\circ}}{360^{\circ}}\times 3.14\times (20\sqrt{2})^2

=\ 628\ cm^2

Also, the area of the square is : =\ 20^2\ =\ 400\ cm^2

Area of the shaded region is : =\ 628\ -\ 400\ =\ 228\ cm^2

Q14 AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig.). If \angle \textup{AOB} = 30\degree , find the area of the shaded region.

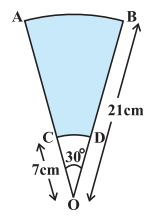
1636091673181

Answer:

Area of the shaded region is = Area of larger sector - Area of smaller sector

=\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times 21^2\ -\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times 7^2

=\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times (21^2\ -\ 7^2)

=\ \frac{308}{3}\ cm^2

Hence the area of the shaded region is \frac{308}{3}\ cm^2.

Q15 In Fig, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

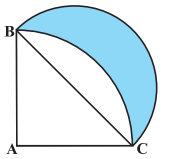
1636091683741

Answer:

Consider \Delta ABC,

BC^2\ =\ AC^2\ +\ AB^2

=\ 14^2\ +\ 14^2

BC\ =\ 14\sqrt{2}\ cm

Area of triangle is :

=\ \frac{1}{2}\times 14\times 14

=\ 98\ cm^2

Now, area of sector is :

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 14^2

=\ 154\ cm^2

And area of semicircle is : -

=\ \frac{1}{2} \pi r^2

=\ \frac{1}{2} \pi \times (7\sqrt{2})^2

=\ 154\ cm^2

Hence the area of the shaded region is : =\ 154\ -\ (154\ -\ 98)\ =\ 98\ cm^2

Q16 Calculate the area of the designed region in fig. common between the two quadrants of circles of radius 8 cm each.

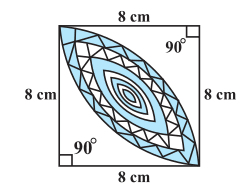
1636091693677

Answer:

It is clear from the figure that the required area (designed area) is the area of the intersection of two sectors.

Area of the sector is:-

=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 8^2

=\ \frac{352}{7}\ cm^2

And, area of the triangle:-

=\ \frac{1}{2}\times 8\times 8\ =\ 32\ cm^2

Hence the area of the designed region is :

=\ 2\left ( \frac{352}{7}\ -\ 32 \right )

=\ \frac{256}{7}\ cm^2

More About NCERT Solutions for Class 10 Maths Exercise 12.3

Class 10 Maths chapter 12 exercise 12.3 Area Related To Circles exercise 12.3 Class 10 Maths, Includes the areas and perimeters which includes plane figures like a wheel, square, parallelogram circle, rectangle and their combinations. NCERT solutions for Class 10 Maths exercise 12.3 mainly focus on the find the shaded area between the two plane figures is given in exercise 12.3 Class 10 Maths.

Also Read| Areas Related to Circles Class 10 Notes

Benefits of NCERT Solutions for Class 10 Maths Exercise 12.3

  • NCERT solutions for Class 10 Math is considered the best material for solving Class 10 Maths chapter 12 exercise 12.3.

  • NCERT Class 10 Maths chapter 12 exercise 12.3, contains all important questions from exam pov and all questions are revised from Class 10 Maths chapter 12 exercise 12.3

  • Exercise 12.3 Class 10 Maths, is based on the combination of figures like circle inscribed in a square, circle inscribed in the square, square with semicircles etc.

Also see-

NCERT Solutions for Class 10 Subject Wise

Frequently Asked Questions (FAQs)

1. What is the value of π ?

We use π=3.14 and also 22/7 for easy calculations 

2. What is the special case of recatngle?

When length of a rectangle is equal to breadth of a rectangle 

Let length =breadth = a

Then area of rectangle = l*b = a²

                                                = Area of square

3. What is the perimeter of a semicircle ?

Perimeter of semicircle= 2πr+ 2r

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Himachal Pradesh Board of Secondary Education 10th Examination

Application Date:02 December,2024 - 16 December,2024

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Four girl students hospitalised in Telangana after eating breakfast
Stalin urges Modi to increase family income ceiling for SC, ST, OBC students for matric scholarships
Over 11.70 lakh children out-of-school in country, maximum in UP: Government to Lok Sabha
PM POSHAN Scheme: Material cost enhanced by 13.70%, revised rates from December 1
Over 7.9 lakh class 9, 10 CBSE students opted for AI subject during 2024-25 session: Government tells LS
PM SHRI: Kerala’s V Sivankutty says Rs 953 crore of SSA funds stopped; Tamil Nadu MOU stalled due to NEP para
Delhi: 40 schools receive bomb threat mail; sender demands USD 30K, nothing suspicious found says police
Back to top