NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles 2021

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles

Edited By Irshad Anwar | Updated on Sep 07, 2023 10:24 PM IST | #CBSE Class 10th

Upcoming Event

CBSE Class 10th Exam Date : 15 Feb' 2025 - 15 Feb' 2025

Area Related To Circle Class 10 NCERT Solution

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles are provided here. These NCERT solutions are developed in accordance of latest syllabus and pattern of CBSE 2023-24. NCERT Solutions are important study materials for students in Class 10. These solutions of class 10 area related to circle help students understand the types of questions that will be asked in the CBSE Class 10 Maths board exams and provide solutions to all areas related to circles, which can aid students in preparing effectively for the CBSE exams. NCERT solutions for Class 10 Maths are available at Careers360 and can help students excel in their board exams by providing them with an advance preparation.

Don't Miss: JEE Main & NEET 2026 Scholarship Test (Class 10): Narayana | Aakash

This Story also Contains

Area Related To Circle Class 10 NCERT Solution
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles PDF Free Download
NCERT Solutions for Class 10 Maths Chapter 12 - Important Formulae
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles (Intext Questions and Exercise)
NCERT Solutions of Class 10 - Subject Wise
Key features of Areas Related To Circles Class 10 NCERT solutions
NCERT Class 10 Maths Solutions - Chapter Wise
NCERT Exemplar solutions - Subject Wise
NCERT Books and NCERT Syllabus

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles

Also Read,

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles PDF Free Download

Download PDF

NCERT Solutions for Class 10 Maths Chapter 12 - Important Formulae

Circumference of a Circle: Circumference = 2πr

Where r = represents the radius of the circle.

Area of a Circle: Area = πr²

Where r signifies the radius of the circle.

Length of an Arc of a Sector - To find the length of an arc within a sector of a circle, given the radius 'r' and the angle in degrees 'θ', the formula is

Arc Length = 2πr(θ/360)

Area of a Sector of a Circle - For calculating the area of a sector within a circle with radius 'r' and angle in degrees 'θ', the formula is

Sector Area = πr²(θ/360)

Area of a Segment of a Circle - The area of a segment of a circle can be found by subtracting the area of the corresponding triangle from the area of the corresponding sector.

Segment Area = Sector Area - Triangle Area

Segment Area = πr²(θ/360) - (1/2)r²sinθ

When considering the distance moved by a wheel in a single revolution, it is equal to the circumference of the wheel.

Number Of Revolutions = Distance Travelled / circumference = d / 2πr

Free download NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles PDF for CBSE Exam.

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles (Intext Questions and Exercise)

NCERT Solutions for Maths Chapter 12 Area Related To Circle Class 10 Excercise: 12.1

Q1 The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has a circumference equal to the sum of the circumferences of the two circles.

Answer:

Circumference of 1st circle is given :

$\\=\ 2\pi r_1\\\\=\ 2\pi \times 19\ =\ 38 \pi\ cm$

And the circumference of the 2nd circle is : $=\ 2\pi \times 9\ =\ 18 \pi\ cm$

Thus the circumference of the new circle is $=\ 18\pi\ +\ 38\pi\ =\ 56\pi\ cm$

or $2\pi r =\ 56\pi$

or $r\ =\ 28\ cm$

Hence the radius of the new circle is 28 cm.

Q2 The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having an area equal to the sum of the areas of the two circles.

Answer:

We know that the area of the circle is : $=\ \pi r^2$

Thus area of a 1st circle : $=\ \pi r^2_1$

or $=\ \pi \times 8^2\ =\ 64 \pi\ cm^2$

And the area of a 2nd circle is : $=\ \pi r^2_2$

or $=\ \pi \times 6^2\ =\ 36\pi\ cm^2$

According to the question area of the new circle is $=\ 64\pi\ +\ 36\pi\ =\ 100\pi\ cm^2$

or $\pi r^2\ =\ 100 \pi$

or $r\ =\ 10\ cm$

Hence the area of the new circle is 10 cm.

Q3 Fig. depicts an archery target marked with its five scoring regions from the center outwards as Gold, Red, Blue, Black, and White. The diameter of the region representing the Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

1648791533512

Answer:

The radius of each scoring region can be found by adding 10.5 in respective colors.

The area of the golden region is : $=\ \pi r^2\ =\ \pi \times 10.5^2\ =\ 346.5\ cm^2$

Similarly area of the red region is = Area of a red score - Area of the golden region

$\\=\ \pi \times 21^2\ -\ \pi \times 10.5^2\\\\=\ 1039.5\ cm^2$

Then the area of the blue region is :

$\\=\ \pi \times (31.5)^2\ -\ \pi \times 21^2\\\\=\ 1732.5\ cm^2$

And the area of the black region is :

$\\=\ \pi \times 42^2\ -\ \pi \times (31.5)^2\\\\=\ 2425.5\ cm^2$

Area of the white region is :

$\\=\ \pi \times 52.5^2\ -\ \pi\times 42^2\\\\=\ 3118.5\ cm^2$

Q4 The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?

Answer:

Let the number of revolution of the wheel be n.

The circumference of the wheel is given by:-

$\\=\ 2\pi r\\\\=\ 2\pi \times 40\ =\ 80\pi\ cm$

Now, the speed of the car is given by:-

$\\=\ 66\ Km/hr\ \\\\=\ 66\times \frac{100000}{60}\ cm/min\ \\\\=\ 110000\ cm/min.$

Thus distance traveled in 10 minutes is: $=\ 1100000\ cm$

According to the question, we get;

$n\times 80\pi\ =\ 1100000$

or $n\ =\ 4375$

Hence the number of revolutions made by the wheel is 4372.

Q5 Tick the correct answer in the following and justify your choice : If the perimeter and the area of a circle are numerically equal, then the radius of the circle is

(A) 2 units
(B) $\pi$ units
(C) 4 units
(D) 7 units

Answer:

Let the radius of the circle be r.

Then according to question, we can write:-

Perimeter = Area

$\\2\pi r\ =\ \pi r^2\\\\r\ =\ 2\ units$

Hence option (A) is correct.

NCERT Solutions for Maths Chapter 12 Area Related To Circle Class 10 Excercise: 12.2

Q1 Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.

Answer:

We know that the area of a sector having radius r and angle $\Theta$ is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2$

Thus the area of the given sector is:-

$\\=\ \frac{60^{\circ}}{360^{\circ}}\times \pi \times 6^2\\\\=\ \frac{132}{7}\ cm^2$

Q2 Find the area of a quadrant of a circle whose circumference is 22 cm.

Answer:

We are given the circumference of the circle.

Thus,

$\\2\pi r\ =\ 22\\\\r\ =\ \frac{11}{\pi}\ cm$

Also, we know that the area of a sector is given by :

$Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2$

It is given that we need to find the area of a quadrant thus $\Theta\ =\ 90^{\circ}$

Hence the area becomes:-

$\\=\ \frac{90}{360^{\circ}}\times \pi \left ( \frac{11}{\pi} \right )^2\\\\=\ \frac{77}{8}\ cm^2$

Q3 The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

Answer:

The minute hand rotates 360 ^o in one hour.

We need to find rotation in 5 min. :-

$=\ \frac{360^{\circ}}{60}\times 5\ =\ 30^{\circ}$

The area of the sector is given by :

$\\Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2\\\\Area=\ \frac{30}{360^{\circ}}\times \pi \times 14^2\\\\Area=\ \frac{154}{3}\ cm^2$

Hence the area swept by minute hand in 5 minutes is .

Q4 A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding : (i) minor segment

Answer:

The angle in the minor sector is 90 ^o .

Thus the area of the sector is given by:-

$\\Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2\\\\Area=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 10^2\\\\Area=\ \frac{1100}{14}\ cm^2\ =\ 78.5\ cm^2$

Now the area of a triangle is:-

$Area\ =\ \frac{1}{2}bh\ =\ \frac{1}{2}\times 10\times 10\ =\ 50\ cm^2$

Thus the area of minor segment = Area of the sector - Area of a triangle

or $=\ 78.5\ -\ 50\ =\ 28.5\ cm^2$

Q4 A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding : (ii) major sector. (Use π = 3.14)

Answer:

The area of the major sector can be found directly by using the formula :

$Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2$

In the case of this, the angle is 360 ^o - 90 ^o = 270 ^o .

Thus the area is : -

$\\=\ \frac{270^{\circ}}{360^{\circ}}\times \pi \times 10\times 10\\\\=\ \frac{3300}{14}\ =\ 235.7\ cm^2$

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (i) the length of the arc

Answer:

The length of the arc is given by:-

$Length\ of\ arc\ =\ \frac{\Theta}{360^{\circ}} \times 2\pi r$

$\\=\ \frac{60^{\circ}}{360^{\circ}} \times 2\times \pi \times 21\\\\=\ 22\ cm$

Hence the length of the arc is 22 cm.

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (ii) area of the sector formed by the arc

Answer:

We know that the area of the sector is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

$\\=\ \frac{60}{360^{\circ}}\ \times \pi \times 21^2\\\\=\ 231\ cm^2$

Thus the area of the sector is 231 cm ² .

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (iii) area of the segment formed by the corresponding chord

Answer:

For the area of the segment, we need to subtract the area of the triangle attached with the area of arc.

Thus consider the triangle:-

It is given that the angle of arc is 60 ^o , or we can say that all angles are 60 ^o (since two sides are equal). Hence it is an equilateral triangle.

Area of triangle is:-

$\\=\ \frac{\sqrt{3}}{4}\times a^2\\\\\\=\ \frac{\sqrt{3}}{4}\times 21^2\\\\=\ \frac{441\sqrt{3}}{4}\ cm^2$

Hence the area of segment is:-

$=\ \left (231\ -\ \frac{441\sqrt{3}}{4} \right )\ cm^2$

Q6 A chord of a circle of radius 15 cm subtends an angle of 60° at the center. Find the areas of the corresponding minor and major segments of the circle.
(Use $\pi = 3.14$ and $\sqrt 3 = 1.73$ )

Answer:

The area of the sector is :

$\\=\ \frac{\Theta }{360^{\circ}}\times \pi r^2\\\\=\ \frac{60^{\circ} }{360^{\circ}}\times \pi \times 15^2\\\\=\ 117.85\ cm^2$

Now consider the triangle, the angle of the sector is 60 ⁰ .

This implies it is an equilateral triangle. (As two sides are equal so will have the same angle. This possible only when all angles are equal i.e., 60 ^o .)

Thus, the area of the triangle is:-

$=\ \frac{\sqrt{3}}{4}\times 15^2$

or $=\ 56.25 \sqrt{3}\ =\ 97.31\ cm^2$

Hence area of the minor segment : $=\117.85\ -\ 97.31\ =\ 20.53\ cm^2$

And the area of the major segment is :

$=\ \pi r^2\ -\ 20.53$

or $=\ \pi\times 15^2\ -\ 20.53$

or $=\ 707.14\ -\ 20.53$

or $=\ 686.6\ cm^2$

Q7 A chord of a circle of radius 12 cm subtends an angle of 120° at the center. Find the area of the corresponding segment of the circle.
(Use $\pi = 3.14$ and $\sqrt3 = 1.73$ )

Answer:

For the area of the segment, we need the area of sector and area of the associated triangle.

So, the area of the sector is :

$=\ \frac{120^{\circ}}{360^{\circ}}\times \pi \times 12^2$

or $=\ 150.72\ cm^2$

Now, consider the triangle:-

Draw a perpendicular from the center of the circle on the base of the triangle (let it be h).

Using geometry we can write,

$\frac{h}{r}\ =\ \cos 60^{\circ}$

or $h\ =\ 6\ cm$

Similarly, $\frac{\frac{b}{2}}{r}\ =\ \sin 60^{\circ}$

or $b\ =\ 12\sqrt{3}\ cm$

Thus the area of the triangle is :

$=\ \frac{1}{2}\times 12\sqrt{3}\times 6$

or $=\ 62.28\ cm^2$

Hence the area of segment is: $=\ 150.72\ -\ 62.28\ =\ 88.44\ cm^2$ .

Q8 A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (i) the area of that part of the field in which the horse can graze.

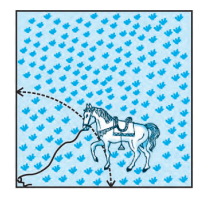
1636091304687

Answer:

The part grazed by the horse is given by = Area of sector

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

$=\ \frac{90^{\circ}}{360^{\circ}}\ \times \pi \times 5^2$

$=\ 19.62\ m^2$

Q8 A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use $\pi = 3.14$ )

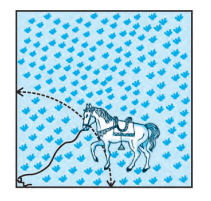
1636091352998

Answer:

When the length of the rope is 10 m, the area grazed will be:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

$=\ \frac{90^{\circ}}{360^{\circ}}\ \times \pi \times 10^2$

$=\ 25 \pi\ m^2$

Hence the change in the grazing area is given by :

$=\ 25 \pi\ -\ \frac{25 \pi}{4}\ =\ 58.85\ m^2$

Q9 A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. Find: (i) the total length of the silver wire required.

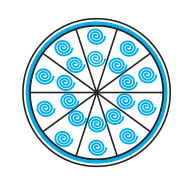
1636091383511

Answer:

The total wire required will be for 5 diameters and the circumference of the brooch.

The circumference of the brooch:-

$\\=\ 2\pi r\\\\=\ 2\times \pi \times \frac{35}{2}\\\\=\ 110\ mm$

Hence the total wire required will be:- _.

Q9 A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. 12.12. Find : (ii) the area of each sector of the brooch.

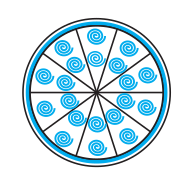
1636091389686

Answer:

The total number of lines present in the brooch is 10 (line starting from the centre).

Thus the angle of each sector is 36 ^o .

The area of the sector is given by:-

$\\Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2\\\\Area=\ \frac{36^{\circ}}{360^{\circ}}\ \times \pi \times \left ( \frac{35}{2} \right )^2\\\\Area=\ \frac{385}{4}\ mm^2$

Q10 An umbrella has 8 ribs that are equally spaced (see Fig. ). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

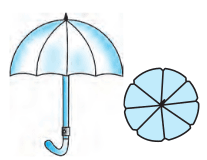
Answer:

It is given that the umbrella has 8 ribs so the angle of each sector is 45 ^o .

Thus the area of the sector is given by:-

$\\Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2\\\\Area=\ \frac{45^{\circ}}{360^{\circ}}\ \times \pi \times 45^2\\\\Area=\ \frac{22275}{28}\ cm^2$

Hence the area between two consecutive ribs is .

Q11 A car has two wipers that do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.

Answer:

The area cleaned by one wiper is:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

or $=\ \frac{115^{\circ}}{360^{\circ}}\ \times \pi \times 25^2$

or $=\ \frac{158125}{252}\ cm^2$

Hence the required area (area cleaned by both blades) is given by:-

$=\ 2\times \frac{158125}{252}\ =\ \frac{158125}{126}\ cm^2$

Q12 To warn ships for underwater rocks, a lighthouse spreads a red-colored light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)

Answer:

The area of the sector is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

In this case, the angle is 80 ^o .

Thus the area is:-

$=\ \frac{80^{\circ}}{360^{\circ}}\ \times \pi \times 16.5^2$

or $=\ 189.97\ Km^2$

Q13 A round table cover has six equal designs as shown in Fig. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs. 0.35 per cm ² . (Use $\sqrt3 = 1.7$ )

Answer:

The angle of each of the six sectors is 60 ^o at the center. $\left ( \because \frac{360^{\circ}}{6}\ =\ 60^{\circ} \right )$

Area of the sector is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

or $=\ \frac{60^{\circ}}{360^{\circ}}\ \times \pi \times 78^2$

or $=\ 410.66\ cm^2$

And the area of the equilateral triangle associated with segment:-

$=\ \frac{\sqrt{3}}{4}\times a^2$

or $=\ \frac{\sqrt{3}}{4}\times 28^2\ =\ 333.2\ cm^2$

Hence the area of segment is : $=\ 410.66\ -\ 333.2\ =\ 77.46\ cm^2$

Thus the total area of design is : $=\6\times 77.46\ =\ 464.76\ cm^2$

So, the total cost for the design is:- $=\ 0.35\times 464.76\ =\ Rs. 162.66$

Q14 Tick the correct answer in the following :

Area of a sector of angle p (in degrees) of a circle with radius R is

(A) $\frac{p}{180}\times 2\pi R$

(B) $\frac{p}{180}\times \pi R^2$

(D) $\frac{p}{720}\times 2\pi R^2$

Answer:

We know that the area of the sector is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

$=\ \frac{p}{360^{\circ}}\ \times \pi r^2$

Hence option (d) is correct.

NCERT Solutions for Maths Chapter 12 A rea Related To Circle Class 10 Excercise: 12.3

Q1 Find the area of the shaded region in Fig, if PQ = 24 cm, PR = 7 cm, and O is the center of the circle.

1648791656559

Answer:

We know that $\angle$ RPQ is 90 ^o as ROQ is the diameter.

RQ can be found using the Pythagoras theorem.

$RP^2\ +\ PQ^2\ =\ QR^2$

or $7^2\ +\ 24^2\ =\ QR^2$

or $QR\ =\ \sqrt{625}\ =\ 25\ cm$

Now, the area of the shaded region is given by = Area of semicircle - Area of $\Delta$ PQR

Area of a semicircle is:-

$=\ \frac{1}{2}\pi r^2$

or $=\ \frac{1}{2}\pi \times \left ( \frac{25}{2} \right )^2$

or $=\ 245.53\ cm^2$

And, the area of triangle PQR is :

$=\ \frac{1}{2}\times 24\times 7\ =\ 84\ cm^2$

Hence the area of the shaded region is :

Q2 Find the area of the shaded region in Fig, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and $\angle AOC = 40\degree$ .

Answer:

The area of a shaded region can be easily found by using the formula of the area of the sector.

Area of the shaded region is given by : Area of sector OAFC - Area of sector OBED

$=\ \frac{40^{\circ}}{360^{\circ}}\times \pi (14)^2\ -\ \frac{40^{\circ}}{360^{\circ}}\times \pi (7)^2$

$=\ \frac{616}{9}\ -\ \frac{154}{9}\ =\ \frac{462}{9}$

$=\ 51.33\ cm^2$

Q3 Find the area of the shaded region in Fig, if ABCD is a square of side 14 cm and APD and BPC are semicircles. 1648791700601

Answer:

Area of the shaded region is given by = Area of the square - Area of two semicircles.

Area of square is : $=\ 14^2\ =\ 196\ cm^2$

And the area of the semicircle is:-

$=\ \frac{1}{2}\pi r^2$

$=\ \frac{1}{2}\pi \times 7^2$

$=\ 77\ cm^2$

Hence the area of the shaded region is given by :

Q4 Find the area of the shaded region in Fig, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as the centre. 1648791737051

Answer:

Area of the shaded region is given by = Area of triangle + Area of the circle - Area of the sector

Area of the sector is : -

$=\ \frac{60^{\circ}}{360^{\circ}}\times \pi\times 6^2$

or $=\ \frac{132}{7}\ cm^2$

And, the area of the triangle is :

$=\ \frac{\sqrt{3}}{4}a^2\ =\ \frac{\sqrt{3}}{4}\times 12^2\ =\ 36\sqrt{3}\ cm^2$

And, the area of the circle is : $=\ \pi r^2$

or $=\ \pi \times 6^2$

or $=\ \frac{792}{7}\ cm^2$

Hence the area of the shaded region is:-

$=\ 36\sqrt{3}\ +\ \frac{792}{7}\ -\ \frac{132}{7}$

or $=\ \left ( 36\sqrt{3}\ +\ \frac{660}{7} \right )\ cm^2$

Q5 From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. Find the area of the remaining portion of the square. 25793

Answer:

Consider the quadrant in the given figure:- We have an angle of the sector as 90 ^o and radius 1 cm.

Thus the area of the quadrant is:-

$=\ \frac{90^{\circ}}{360^{\circ}}\times \pi\times 1^2$

or $=\ \frac{22}{28}\ cm^2$

And the area of the square is : $=\ side^2$

$=\ 4^2$

$=\ 16\ cm^2$

And, the area of the circle is:-

$=\ \pi r^2\ =\ \pi \times 1^2\ =\ \pi\ cm^2$

Hence the area of the shaded region is: = Area of the square - Area of the circle - 4 (Area of quadrant)

or $=\ 16\ -\ \frac{22}{7}\ -\ 4\left ( \frac{22}{28} \right )$

or $=\ \frac{68}{7}\ cm^2$

Q6 In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. Find the area of the design.

Answer:

Assume the center of the circle to be point C and AD as the median of the equilateral triangle.

Then we can write:-

$AO\ =\ \frac{2}{3}AD$

or $32\ =\ \frac{2}{3}AD$

Thus $AD\ =\ 48\ cm$

Consider $\Delta$ ABD,

$AB^2\ =\ AD^2\ +\ BD^2$

or $AB^2\ =\ 48^2\ +\ \left ( \frac{AB}{2} \right )^2$

or $AB\ =\ 32\sqrt{3}\ cm$

Thus the area of an equilateral triangle is:-

$=\ \frac{\sqrt{3}}{4}\times \left ( 32\sqrt{3} \right )^2$

or $=\ 768\sqrt{3}\ cm^2$

And the area of the circle is : $=\ \pi r^2\ =\ \pi\times 32^2$

or $=\ \frac{22528}{7} cm^2$

Hence the area of the design is:-

$=\ \left ( \frac{22528}{7}\ -\ 768 \sqrt{3} \right )\ cm^2$

Q7. In Fig, ABCD is a square of side 14 cm. With centers A, B, C, and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.

Answer:

It is clear from the figure that the area of all sectors is equal (due to symmetry).

Also, the angle of the sector is 90 ^o and the radius is 7 cm.

Thus the area of the sector is:-

$=\ \frac{90^{\circ}}{360^{\circ}}\times \pi (7)^2$

or $=\ \frac{77}{2}\ cm^2$

And, the area of the square is : $=\ a^2\ =\ 14^2\ =\ 196\ cm^2$

Hence the area of the shaded region is :

$=\ 196\ -\ 4\times \frac{77}{2}$

$=\ 42\ cm^2$

Q8 Fig. depicts a racing track whose left and right ends are semicircular.

1636091567493

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :

(i) the distance around the track along its inner edge

Answer:

The distance around the track is Length of two straight lines + Length of two arcs.

Length of the arc is -

$=\ \frac{1}{2}\times 2\pi r$

$=\ \frac{1}{2}\times 2\pi \times 30\ =\ 30\pi\ m$

Thus the length of the inner track is :

$=\ 106\ +\ 30\pi\ +\ 106\ +\ 30\pi$

$=\ 212\ +\ 60\pi$

$=\ \frac{2804}{7}\ m$

Q8 Fig. depicts a racing track whose left and right ends are semicircular.

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :

(ii) the area of the track.

Answer:

The area of track = Area of outer structure - Area of inner structure.

Area of outer structure is: = Area of square + Area of 2 semicircles

$=\ 106\times 80\ +\ \frac{1}{2}\pi (40)^2\ +\ \frac{1}{2}\pi (40)^2\ m^2$

And, area of inner structure: = Area of inner square + Area of 2 inner semicircles

$=\ 106\times 60\ +\ \frac{1}{2}\pi (30)^2\ +\ \frac{1}{2}\pi (30)^2\ m^2$

Thus the area of the track is :

$\\=\ 106\times 80\ +\ \frac{1}{2}\pi (40)^2\ +\ \frac{1}{2}\pi (40)^2\ -\ \left ( 106\times 60\ +\ \frac{1}{2}\pi (30)^2\ +\ \frac{1}{2}\pi (30)^2 \right )\\\\=\ 4320\ m^2$

Hence the area of the track is 4320 m ² .

Q9 In Fig, AB, and CD are two diameters of a circle (with center O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

1636091578284

Answer:

Firstly, the area of the smaller circle is :

$=\ \pi r^2$

$=\ \pi \times \left ( \frac{7}{2} \right )^2$

$=\ \frac{77}{2}\ cm^2$

Now, the area of $\Delta ABC$ :-

$=\ \frac{1}{2}\times AB\times OC$

or $=\ \frac{1}{2}\times 14\times 7\ =\ 49\ cm^2$

And, the area of the bigger semicircle is :

$=\ \frac{1}{2}\pi r^2$

$=\ \frac{1}{2}\pi \times 7^2$

$=\ 77\ cm^2$

Hence the area of the shaded region is:-

$=\ \frac{77}{2}\ +\ 77\ -\ 49$

$=\ 66.5\ cm^2$

Therefore the area of the shaded region is 66.5 cm ² .

Q10 The area of an equilateral triangle ABC is 17320.5 cm ² . With each vertex of the triangle as the centre, a circle is drawn with a radius equal to half the length of the side of the triangle (see Fig.). Find the area of the shaded region. (Use $\pi = 3.14$ and $\sqrt3 = 1.73205$ )

1636091615101

Answer:

Area of an equilateral triangle is:-

$=\ \frac{\sqrt{3}}{4}\times a^2$

$\frac{\sqrt{3}}{4}\times a^2\ =\ 17320.5$

$a\ =\ 200\ cm$

Now, consider the sector:- Angle of the sector is 60 ^o and the radius is 100 cm.

Thus the area of the sector:-

$=\ \frac{60^{\circ}}{360^{\circ}}\times \pi \times 100^2$

$=\ \frac{15700}{3}\ cm^2$

Thus the area of the shaded region is :

$=\ 17320.5\ -\ 3\times \frac{15700}{3}$

$=\ 1620.5\ cm^2$

Q11 On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig.). Find the area of the remaining portion of the handkerchief.

1636091628689

Answer:

Since one side of the square has 3 circles, thus the side of the square is 42 cm.

Area of the square : $=\ a^2\ =\ 42^2\ =\ 1764\ cm^2$

And, area of a circle :

$=\ \pi r^2\ =\ \frac{22}{7}\times 7^2$

$=\ 154\ cm^2$

Hence the area of the remaining portion is : $=\ 1764\ -\ 9\times 154$

$=\ 378\ cm^2$

Q12 In Fig, OACB is a quadrant of a circle with center O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB

1636091641153

Answer:

The quadrant OACB is a sector with angle 90 ^o and radius 3.5 cm.

Thus the area of the quadrant is:-

$=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 3.5^2$

$=\ \frac{77}{8}\ cm^2$

Hence the area of the quadrant is .

Q12 In Fig, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (ii) shaded region.

1636091648074

Answer:

For area of shaded region we need to find area of the triangle.

Area of triangle is:-

$=\ \frac{1}{2}\times 3.5\times 2$

$=\ 3.5\ cm^2$

Hence the area of the shaded region is = Area of the quadrant - Area of triangle

$=\ \frac{77}{8}\ -\ 3.5$

$=\ \frac{49}{8}\ cm^2$

Q13 In Fig, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use $\pi = 3.14$ )

1636091662355

Answer:

In the given figure we need to find the radius of the circle:-

Consider $\Delta$ OAB,

$OB^2\ =\ OA^2\ +\ AB^2$

$=\ 20^2\ +\ 20^2$

$OB\ =\ 20\sqrt{2}\ cm$

Thus area of quadrant:-

$=\ \frac{90^{\circ}}{360^{\circ}}\times 3.14\times (20\sqrt{2})^2$

$=\ 628\ cm^2$

Also, the area of the square is : $=\ 20^2\ =\ 400\ cm^2$

Area of the shaded region is : $=\ 628\ -\ 400\ =\ 228\ cm^2$

Q14 AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig.). If $\angle \textup{AOB} = 30\degree$ , find the area of the shaded region.

1636091673181

Answer:

Area of the shaded region is = Area of larger sector - Area of smaller sector

$=\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times 21^2\ -\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times 7^2$

$=\ \frac{30^{\circ}}{360^{\circ}}\times \pi \times (21^2\ -\ 7^2)$

$=\ \frac{308}{3}\ cm^2$

Hence the area of the shaded region is $\frac{308}{3}\ cm^2.$

Q15 In Fig, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

1636091683741

Answer:

Consider $\Delta$ ABC,

$BC^2\ =\ AC^2\ +\ AB^2$

$=\ 14^2\ +\ 14^2$

$BC\ =\ 14\sqrt{2}\ cm$

Area of triangle is :

$=\ \frac{1}{2}\times 14\times 14$

$=\ 98\ cm^2$

Now, area of sector is :

$=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 14^2$

$=\ 154\ cm^2$

And area of semicircle is : -

$=\ \frac{1}{2} \pi r^2$

$=\ \frac{1}{2} \pi \times (7\sqrt{2})^2$

$=\ 154\ cm^2$

Hence the area of the shaded region is :

Q16 Calculate the area of the designed region in fig. common between the two quadrants of circles of radius 8 cm each.

1636091693677

Answer:

It is clear from the figure that the required area (designed area) is the area of the intersection of two sectors.

Area of the sector is:-

$=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 8^2$

$=\ \frac{352}{7}\ cm^2$

And, area of the triangle:-

$=\ \frac{1}{2}\times 8\times 8\ =\ 32\ cm^2$

Hence the area of the designed region is :

$=\ 2\left ( \frac{352}{7}\ -\ 32 \right )$

$=\ \frac{256}{7}\ cm^2$

NCERT Solutions of Class 10 - Subject Wise

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Key features of Areas Related To Circles Class 10 NCERT solutions

Enhanced Conceptual Understanding: These ch 12 maths class 10 solutions serve as a valuable tool for students seeking to grasp circle-related concepts thoroughly.

Visual Clarity: The ch 12 maths class 10 solutions are thoughtfully supplemented with diagrams, facilitating a more interactive and comprehensive learning journey.

Accessible Language: The language employed in these chapter 12 maths class 10 solutions is intentionally straightforward, ensuring that students can easily grasp the content.

Step-by-Step Guidance: The chapter 12 maths class 10 solutions follow a methodical, step-by-step approach, aiding students in building a strong foundation and understanding the fundamentals with ease.

Individualized Learning: Students have the flexibility to tackle complex problems at their own pace, which fosters self-directed learning and builds problem-solving skills.

Resource Diversity: These ch 12 class 10 maths solutions open doors for students to explore NCERT solutions across various classes and subjects.

Expertly Crafted: These ch 12 class 10 maths solutions are meticulously prepared by experienced educators at Careers360, who prioritize providing clarity on key concepts and nurturing students' problem-solving abilities

Also students can get the solutions for individual exercise-

NCERT Class 10 Maths Solutions - Chapter Wise

Chapter No.	Chapter Name
Chapter 1	Real Numbers
Chapter 2	Polynomials
Chapter 3	Pair of Linear Equations in Two Variables
Chapter 4	Quadratic Equations
Chapter 5	Arithmetic Progressions
Chapter 6	Triangles
Chapter 7	Coordinate Geometry
Chapter 8	Introduction to Trigonometry
Chapter 9	Some Applications of Trigonometry
Chapter 10	Circles
Chapter 11	Constructions
Chapter 12	Areas Related to Circles
Chapter 13	Surface Areas and Volumes
Chapter 14	Statistics
Chapter 15	Probability

NCERT Exemplar solutions - Subject Wise

Students can also find area related to circle class 10 questions with solutions

NCERT Books and NCERT Syllabus

Tips to Use NCERT Solutions for Class 10 Maths Chapter 12

Before starting with this chapter, be well-versed with basic concepts of circles, squares, rectangles, triangles, etc.
Learn some formulae related to sectors and segments from the NCERT Class 10 books.
Go through some examples given in the textbook and Class 10 Maths Chapter 12 NCERT solutions to understand the approach of solving the problems.
After covering the above-said points, it is time to put efforts into practice by practicing the practice exercises.
During the practice, one can refer to NCERT solutions for Class 10 Maths chapter 12 to know the correct answer or to know how to solve a particular question.

Happy Learning!

Frequently Asked Questions (FAQs)

1. How many exercises are there in NCERT Solutions for class 10 areas related to circles?

NCERT solutions for class 10 maths areas related to circles includes 3 exercises with a total of 35 questions. The first exercise covers 5 questions, the second exercise covers 14 questions, and the last exercise covers 16 questions related to the perimeter and area of a circle, areas of a sector and segment of a circle, and areas of combinations of plane figures. Interested students can study area related to circle class 10 pdf online at careers360 website.

2. What are the important concepts from an exam perspective in areas related to circles class 10 solutions?

The key concepts emphasized in area related to circle class 10 solutions that are important from an exam perspective include the introduction to the area of a circle, perimeter and area of a circle, areas of sector and segment of a circle, and areas of combinations of plane figures. Additionally, a summary of the entire chapter class 10 maths areas related to circles is provided

3. What is the significance of studying NCERT Solutions for Class 10 Maths Chapter 12?

The importance of studying class 10 ch area related to circles lies in its ability to provide students with a clear understanding of the question paper pattern and types of questions that may be asked in the board exams, including a mix of repeating, short and long answer, and multiple-choice questions. Practicing a variety of questions can increase students' confidence and increase their chances of success. For ease, students can study areas related to circles class 10 pdf both online and offline mode.

4. Which is the best book for CBSE class 10 maths ?

NCERT textbook is the best book for CBSE class 10 maths. Most of the questions in CBSE class 10 board exam are directly asked from NCERT textbook. All you need to do is rigorous practice of the questions given in the NCER textbook.

5. Which are the most difficult chapter in the NCERT class 10 maths ?

Students consider trigonometry that is introduction to trigonometry and application of trigonometry is most difficult chapter in CBSE class 10 maths. With the regular practice you will get conceptual clarity and will be able to have a strong grip on Trigonometry.

Also Read

NCERT Class 10 Maths Notes - Download Chapter Wise PDFs

The Human Eye and The Colorful world Class 10th Notes- Free NCERT Class 10 Science Chapter 11 Notes - Download PDF

NCERT Class 10 Science Chapter 14 Notes Sources Of Energy - Download PDF

Magnetic Effects of Electric Current Class 10th Notes - Free NCERT Class 10 Science Chapter 13 Notes - Download PDF

Electricity Class 10th Notes - Free NCERT Class 10 Science Chapter 12 Notes - Download PDF

Light- Reflection and Refraction Class 10th Notes- Free NCERT Class 10 Science Chapter 10 Notes - Download PDF

NCERT Syllabus for Class 10 Maths 2024-25 - Download Free PDF

NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.1 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Class 10 Science Chapter 6 Life Processes

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations

NCERT Exemplar Class 10 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 10 Science Solutions Chapter 1 Chemical Reactions and Equations

NCERT Exemplar Class 10 Science Solutions - Chapter Wise Problems with Solutions

Articles

UCO Result 2024-25- Check Unified Cyber Olympiad Result @ unifiedcouncil.com

Dec 14, 2024

Navodaya Entrance Exam Date 2025 OUT Class 6 & 9: Application Form, Admit Card, Result

Dec 14, 2024

Navodaya Vidyalaya Admit Card 2025 (Out) Class 6 & 9: Download JNV Admit Card PDF

Dec 14, 2024

NRTS Registrations 2024: NRTS Scholarship Login, Application Window Open

Dec 13, 2024

Class 10 Science Weightage 2024-25 Blueprint by CBSE, Chapter-Wise Weightage, Marking Scheme

Dec 09, 2024

CBSE Date Sheet 2025 Class 10th OUT; Download CBSE 10th Exam Time Table PDF

Dec 06, 2024

Class 10 Social Science Blueprint 2025 by CBSE: Chapter-Wise Weightage & Exam Pattern

Dec 05, 2024

CBSE Class 10 Toppers Answer Sheet 2025 - Check Here

Nov 29, 2024

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Mock Test

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Admit Card

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Himachal Pradesh Board of Secondary Education 10th Examination

Application Date:02 December,2024 - 16 December,2024

Exam Pattern

Admit Card

Result

Himachal Pradesh Board of Secondary Education 12th Examination

Application Date:02 December,2024 - 16 December,2024

Result

Exam Pattern

View All School Exams

Certifications By Top Providers

My SQL Basics

Via Great Learning

Digital Banking Business Model

Via State Bank of India

Full-Stack Web Development

Via Masai School

Business Analytics Foundations

Via PW Skills

Full-Stack Android Development

Via Masai School

Forensic Science DNA Analysis

Via University of Cambridge, Cambridge

1115 courses

816 courses

394 courses

295 courses

Harvard University, Cambridge

98 courses

University of Michigan, Ann Arbor

83 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

Environmental Studies

History

Psychology

Artificial Intelligence

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Delaware, Newark

Newark, DE 19716

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Study in Ireland Without IELTS 2024: Universities List, Process, Eligibility

12 min ⋆ Oct 11, 2024 09:10 AM IST

IELTS Syllabus and Pattern 2024 (Section Wise): Download PDF Here!

11 min ⋆ Oct 14, 2024 08:10 AM IST

CAE Exam (C1 Advanced) 2024: Fees, Syllabus, Pattern, Validity

8 min ⋆ Jul 05, 2024 12:07 PM IST

PTE Exam Pattern 2024: Format, Structure, Sections, Marking Scheme

13 min ⋆ Oct 14, 2024 09:10 AM IST

Cheapest Universities in California for International Students 2024

7 min ⋆ Sep 04, 2024 11:09 AM IST

Cheapest and Affordable Universities in France for International Students in 2025

10 min ⋆ Dec 13, 2024 12:12 PM IST

Related E-books & Sample Papers

CBSE Class 10 Social Science Sample Paper with Solution 2024-25 PDF

550+ Downloads

CBSE Class 10 Mathematics (Standard) Sample Paper with Solution 2024-25 PDF

328+ Downloads

CBSE Class 10 Mathematics (Basic) Sample Paper with Solution 2024-25 PDF

180+ Downloads

CBSE Class 10 Hindi B Sample Paper with Solution 2024-25 PDF

79+ Downloads

CBSE Class 10 Hindi A Sample Paper with Solution 2024-25 PDF

48+ Downloads

CBSE Class 10 English (Language & Literature) Sample Paper with Solution 2024-25 PDF

69+ Downloads

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?

sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

Starting Point:
- Determine your starting point in Aligarh or the nearby area.
Use Google Maps:
- Open Google Maps on your phone or computer.
- Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
- Follow the navigation instructions provided by Google Maps.
By Local Transport:
- Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
- Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.
Landmarks to Look For:
- As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.
Ask for Directions:
- If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.
Final Destination:
- Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer

sai raja 01 September,2024

show the previous year exams ?

Hello Aspirant, Hope your doing great, your question was incomplete and regarding what exam your asking.

Read Complete Answer

SWETCHCHA MISKA 10 July,2024

as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer

Manasvini Gupta 23 July,2024

i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer

Ashvadha 03 July,2024

i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer

sadafreen356 03 July,2024

View All

Stay up-to date with CBSE Class 10th News

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Central Board of Secondary Education Class 10th Examination

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles

Area Related To Circle Class 10 NCERT Solution

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles PDF Free Download

NCERT Solutions for Class 10 Maths Chapter 12 - Important Formulae

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles (Intext Questions and Exercise)

Answer:

Answer:

Answer:

Answer:

Answer:

Q1 Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

NCERT Solutions of Class 10 - Subject Wise

Pearson | PTE

Key features of Areas Related To Circles Class 10 NCERT solutions

NCERT Class 10 Maths Solutions - Chapter Wise

NCERT Exemplar solutions - Subject Wise

NCERT Books and NCERT Syllabus

Tips to Use NCERT Solutions for Class 10 Maths Chapter 12

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Certifications By Top Providers

Explore Top Universities Across Globe

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

Popular CBSE Class 10th Questions

Colleges After 12th

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Stay up-to date with CBSE Class 10th News

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10