NCERT Solutions for Class 10 Maths Chapter 10 Circles

Q1: How many tangents can a circle have?

Answer:

The lines that intersect the circle exactly at one single point are called tangents. In a circle, there can be infinitely many tangents.

Q2: Fill in the blanks :
(1) A tangent to a circle intersects it in_________ point (s).
(2) A line intersecting a circle in two points is called a _____.
(3) A circle can have ________ parallel tangents at the most.
(4) The common point of a tangent to a circle and the circle ______

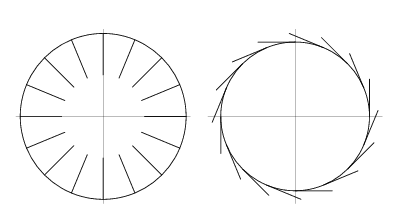
Answer:

(1) one
A tangent of a circle intersects the circle exactly in one single point.

(2) secant
It is a line that intersects the circle at two points.

(3) Two,
There can be only two parallel tangents to a circle.

(4) point of contact
The common point of a tangent and a circle.

Q3: A tangent PQ at a point P of a circle of radius 5 cm meets a line through the center O at a point Q so that OQ = 12 cm. The Length PQ is :

(A) 12 cm

(B) 13 cm

(C) 8.5 cm

(D) $\sqrt { 119}$ cm.

Answer:

The correct option is (D) = $\sqrt { 119}$ cm

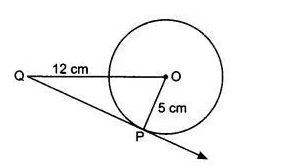
It is given that the radius of the circle is 5 cm. OQ = 12 cm
According to the question,
We know that $\angle QPO=90^0$
So, triangle OPQ is a right-angle triangle. By using Pythagoras theorem,
$PQ =\sqrt{OQ^2-OP^2}=\sqrt{144-25}$
$=\sqrt{119}$ cm

Q4: Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.

Answer:

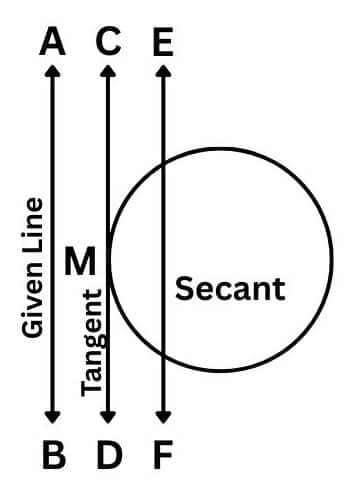
AB is the given line, and line CD is the tangent to a circle at point M that is parallel to line AB. The line EF is a second parallel to the AB.

Q1: From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the center is 25 cm. The radius of the circle is

(A) 7 cm

(B) 12 cm

(C) 15 cm

(D) 24.5 cm

Answer:

The correct option is (A) = 7 cm

Given that,
The length of the tangent (QT) is 24 cm and the length of OQ is 25 cm.
Suppose the length of the radius OTise $l$ cm.
We know that $\Delta OTQ$ is a right-angle triangle. So, by using Pythagoras theorem-

$\\OQ^2 = TQ^2+OT^2\\\\ l = \sqrt{25^2-24^2}\\\\OT = l=\sqrt{49}$

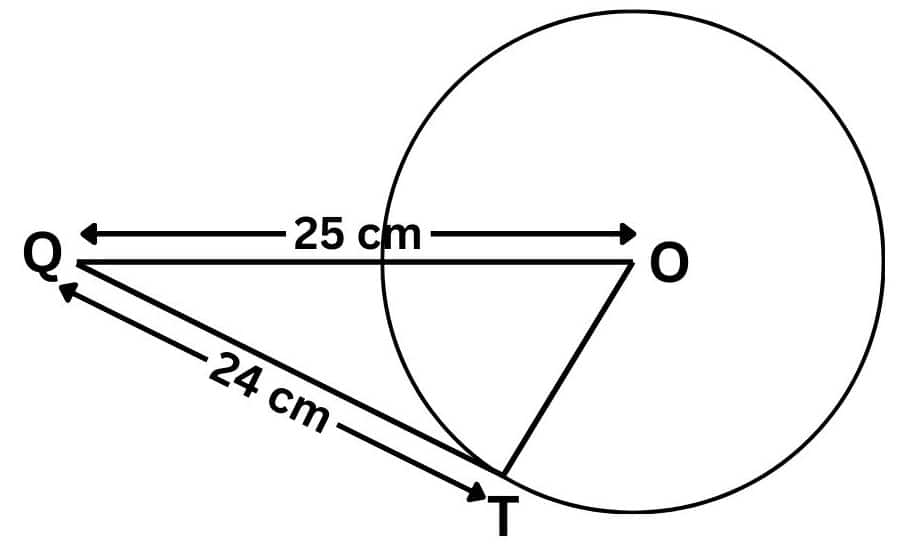
OT = 7 cm

Q2: In Fig. 10.11, if TP and TQ are the two tangents to a circle with center O so that $\angle$ POQ = $11 0 ^\circ$, then $\angle$ PTQ is equal to

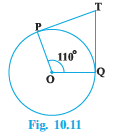
(A) $60 ^\circ$

(B) $70 ^\circ$

(C) $80 ^\circ$

(D) $9 0 ^\circ$

Answer:

The correct option is (b)

In figure, $\angle POQ = 110^0$
Since POQT is quadrilateral. Therefore the sum of the opposite angles is 180

$\\\Rightarrow \angle PTQ +\angle POQ = 180^0\\\\\Rightarrow \angle PTQ = 180^0-\angle POQ$
$= 180^0-100^0$
$= 70^0$

Q3: If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of $80 ^\circ$ then $\angle$ POA is equal to

(A) 50°

(B) 60°

(C) 70°

(D) 80°

Answer:

The correct option is (A)

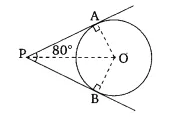
It is given that, tangent PA and PB from point P inclined at $\angle APB = 80^0$
In triangle $\Delta$ OAP and $\Delta$ OBP
$\angle OAP = \angle OBP = 90$
OA =OB (radii of the circle)
PA = PB (tangents of the circle)

Therefore, by SAS congruence
$\therefore \Delta OAP \cong \Delta OBP$

By CPCT, $\angle OPA = \angle OPB$
Now, $\angle$ OPA = 80/4 = 40

In $\Delta$ PAO,
$\angle P + \angle A + \angle O = 180$
$\angle O = 180 - 130$
= 50

Q4: Prove that the tangents drawn at the ends of the diameter of a circle are parallel.

Answer:

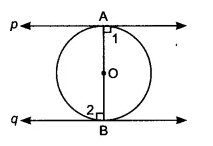
Let line $p$ and line $q$ be two tangents of a circle and AB is the diameter of the circle.
OA and OB are perpendicular to the tangents $p$ and $q$ respectively.
therefore,
$\angle1 = \angle2 = 90^0$

$\Rightarrow$ $p$ || $q$ { $\angle$ $\because$ 1 & $\angle$ 2 are alternate angles}

Q5: Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Answer:

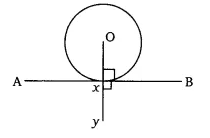
In the above figure, the line AXB is tangent to a circle with centre O. Here, OX is perpendicular to the tangent AXB ( $OX\perp AXB$ ) at the point of contact X.
Therefore, we have,
$\angle$ BXO + $\angle$ YXB = $90^0+90^0=180^0$

$\therefore$ OXY is a collinear
$\Rightarrow$ OX is passing through the centre of the circle.

Q6: The length of a tangent from point A at a distance of 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Answer:

Given that,
the length of the tangent from point A (AP) is 4 cm and the length of OA is 5 cm.
Since $\angle$ APO = 90 0
Therefore, $\Delta$ APO is a right-angle triangle. By using Pythagoras' theorem;

$OA^2=AP^2+OP^2$
$5^2 = 4^2+OP^2$
$OP=\sqrt{25-16}=\sqrt{9}$
$OP = 3 cm$

Q7: Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Answer:

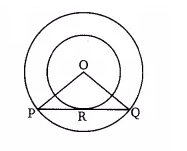
In the above figure, Pq is the chord to the larger circle, which is also tangent to a smaller circle at the point of contact R.
We have,
radius of the larger circle OP = OQ = 5 cm
radius of the small circle (OR) = 3 cm

OR $\perp$ PQ [since PQ is tangent to a smaller circle]

According to the question,

In $\Delta$ OPR and $\Delta$ OQR
$\angle$ PRO = $\angle$ QRO {both $90^0$ }

OR = OR {common}
OP = OQ {both radii}

By RHS congruence $\Delta$ OPR $\cong$ $\Delta$ OQR
So, by CPCT
PR = RQ
Now, In $\Delta$ OPR,
by using Pythagoras theorem,
$PR = \sqrt{25-9} =\sqrt{16}$
PR = 4 cm
Hence, PQ = 2.PR = 8 cm

Q8: A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC

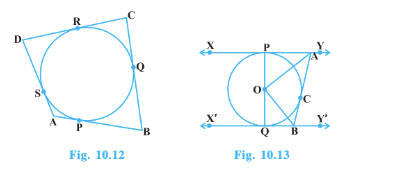
Answer:

To prove- AB + CD = AD + BC
Proof-
We have,
Since the length of the tangents drawn from an external point to a circle is equal
AP =AS .......(i)
BP = BQ.........(ii)
AS = AP...........(iii)
CR = CQ ...........(iv)

By adding all the equations, we get;

AP + BP +RD+ CR = AS +DS +BQ +CQ
$\Rightarrow$ (AP + BP) + (RD + CR) = (AS+DS)+(BQ + CQ)
$\Rightarrow$ AB + CD = AD + BC

Hence proved.

Q9: In Fig. 10.13, XY and X'Y'are two parallel tangents to a circle with center O and another tangent AB with a point of contact C intersecting XY at A and X'Y' at B. Prove that $\angle$ AOB = 90°.

Answer:

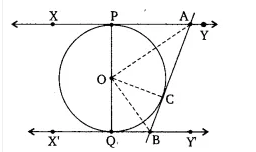
To prove- $\angle$ AOB = $90^0$
Proof-
In $\Delta$ AOP and $\Delta$ AOC,
OA =OA [Common]
OP = OC [Both radii]
AP =AC [tangents from external point A]
Therefore by SSS congruence, $\Delta$ AOP $\cong$ $\Delta$ AOC
and by CPCT, $\angle$ PAO = $\angle$ OAC
$\Rightarrow \angle PAC = 2\angle OAC$ ..................(i)

Similarly, from $\Delta$ OBC and $\Delta$ OBQ, we get;
$\angle$ QBC = 2. $\angle$ OBC.............(ii)

Adding eq (1) and eq (2)

$\angle$ PAC + $\angle$ QBC = 180
2( $\angle$ OBC + $\angle$ OAC) = 180
( $\angle$ OBC + $\angle$ OAC) = 90

Now, in $\Delta$ OAB,
The sum of the interior angles is 180.
So, $\angle$ OBC + $\angle$ OAC + $\angle$ AOB = 180
$\therefore$ $\angle$ AOB = 90
Hence proved.

Q10: Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.

Answer:

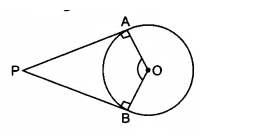
To prove - $\angle APB + \angle AOB = 180^0$
Proof-
We have, PA and PB are two tangents, and B and A are the points of contact of the tangent to a circle. And $OA\perp PA$, $OB\perp PB$ (since tangents and radius are perpendiculars)

According to the question,
In quadrilateral PAOB,
$\angle$ OAP + $\angle$ APB + $\angle$ PBO + $\angle$ BOA = $360^0$
90 + $\angle$ APB + 90 + $\angle$ BOA = 360
$\angle APB + \angle AOB = 180^0$
Hence proved

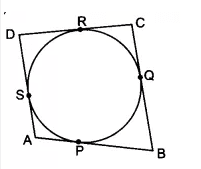
Q11: Prove that the parallelogram circumscribing a circle is a rhombus.

Answer:

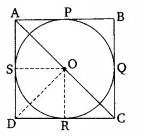
To prove - the parallelogram circumscribing a circle is a rhombus
Proof-
ABCD is a parallelogram that circumscribes a circle with centre O.
P, Q, R, and Sand are the points of contact on sides AB, BC, CD, and DA respectively.
AB = CD .and AD = BC...........(i)
It is known that tangents drawn from an external point are equal in length.
RD = DS ...........(ii)
RC = QC...........(iii)
BP = BQ...........(iv)
AP = AS .............(v)
By adding eq (ii) to eq (v) we get;
(RD + RC) + (BP + AP) = (DS + AS) + (BQ + QC)
CD + AB = AD + BC
$\Rightarrow$ 2AB = 2AD [from equation (i)]
$\Rightarrow$ AB = AD
Now, AB = AD and AB = CD
$\therefore$ AB = AD = CD = BC

Hence, ABCD is a rhombus.

Q12: A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC.

Answer:

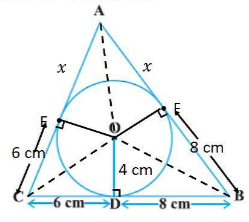
Consider the above figure. Assume centre O touches the sides AB and AC of the triangle at points E and F respectively.

Let the length of AE be x.

Now in $\bigtriangleup ABC$ ,

$CF = CD = 6$ (tangents on the circle from point C)

$BE = BD = 6$ (tangents on the circle from point B)

$AE = AF = x$ (tangents on the circle from point A)

Now AB = AE + EB

$AB = AE + EB$
$ ⇒AB = x + 8$
$BC = BD + DC$
$⇒ BC = 8+6 = 14$
$CA = CF + FA$
$⇒ CA = 6 + x\\\\$

Now
$s = \frac{(AB + BC + CA )}2$
$ ⇒s = \frac{(x + 8 + 14 + 6 +x)}2$
$ ⇒s = \frac{(2x + 28)}2$
$⇒ s = x + 14$

Area of triangle $\bigtriangleup ABC$

$\\=\sqrt{s×(s-a)×(s-b)×(s-c)}$
$=\sqrt{(14+x)×[(14+x)-14]×[(14+x)-(6+x)]×[(14+x)-(8+x)]}$
$=4\sqrt{3(14x+x^2)}$
Now the area of $\bigtriangleup OBC$

$\\= (\frac12)×OD×BC\\\\ = (\frac12)×4×14\\\\ = \frac{56}2 = 28$
Area of $\bigtriangleup OCA$

$\\= (\frac12)×OF×AC \\\\= (\frac12)×4×(6+x) \\\\= 2(6+x) \\\\= 12 + 2x$

Area of $\bigtriangleup OAB$

$\\= (\frac12)×OE×AB \\\\= (\frac12)×4×(8+x) \\\\= 2(8+x) \\\\= 16 + 2x$

Now Area of the $\bigtriangleup ABC$ = Area of $\bigtriangleup OBC$ + Area of $\bigtriangleup OCA$ + Area of $\bigtriangleup OAB$

$⇒ 4\sqrt{3x(14+x)}= 28 + 12 + 2x + 16 + 2x $
$ ⇒4\sqrt{3x(14+x)} = 56 + 4x $
$⇒ 4\sqrt{3x(14+x)} = 4(14 + x) $
$⇒ \sqrt{3x(14+x)}= 14 + x$

On squaring both sides, we get,

$⇒3x(14 + x) = (14 + x)^2$
$ ⇒3x = 14 + x $
$⇒3x - x = 14$
$⇒ 2x = 14$
$ ⇒x = \frac{14}2$
$⇒x = 7$

Hence

AB = x + 8

⇒ AB = 7+8

⇒ AB = 15

AC = 6 + x

⇒ AC = 6 + 7

⇒ AC = 13

Answer- AB = 15 and AC = 13

Q13: Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.

Answer:

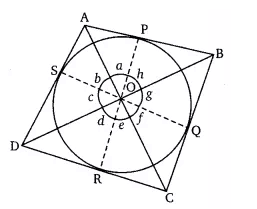
Given- ABCD is a quadrilateral circumscribing a circle. P, Q, R, and S are the points of contact on sides AB, BC, CD, and DA respectively.

To prove-
$\\\angle AOB + \angle COD =180^0\\ \angle AOD + \angle BOC =180^0$
Proof -
Join OP, OQ, O, R, and OS
In triangle $\Delta$ DOS and $\Delta$ DOR,
OD =OD [common]
OS = OR [radii of the same circle]
DR = DS [length of tangents drawn from an external point are equal ]
By SSS congruency, $\Delta$ DOS $\cong$ $\Delta$ DOR,
and by CPCT, $\angle$ DOS = $\angle$ DOR
$\angle c = \angle d$ .............(i)

Similarly,
$\\\angle a = \angle b\\ \angle e = \angle f\\ \angle g =\angle h$ ...............(2, 3, 4)

$\therefore 2(\angle a +\angle e +\angle h+\angle d) = 360^0$
$\\(\angle a +\angle e) +(\angle h+\angle d) = 180^0\\ \angle AOB + \angle DOC = 180^0$
SImilarily, $\angle AOD + \angle BOC = 180^0$

Hence proved.