NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Q1: Form the pair of linear equations in the following problems and find their solutions graphically.

(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.

Answer:

Let the number of boys be x and the number of girls be y.

Now, according to the question,

Total number of students in the class = 10, i.e.

$\Rightarrow x+y=10.....(1)$

And, given that the number of girls is 4 more than the number of boys, it means $x=y+4$

$\Rightarrow x-y=4..........(2)$

Different points (x, y) satisfying equation (1)

Different points (x,y) satisfying equation (2)

Graph,

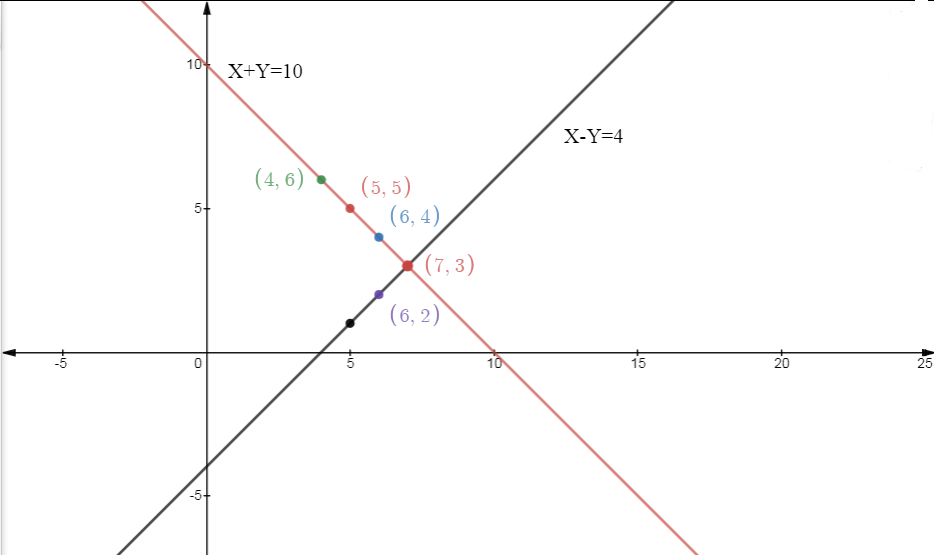
As we can see from the graph, both lines intersect at the point (7,3). that is x= 7 and y = 3, which means the number of boys in the class is 7 and the number of girls in the class is 3.

Q1: Form the pair of linear equations in the following problems and find their solutions graphically.

(ii) 5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together cost Rs 46. Find the cost of one pencil and that of one pen.

Answer:

Let the price of 1 pencil be x, and y be the price of 1 pen.

Now, according to the question

$5x+7y=50......(1)$

And

$7x+5y=46......(2)$

Now, the points (x,y) that satisfy the equation (1) are

And, the points (x,y) that satisfy the equation (2) are

The Graph,

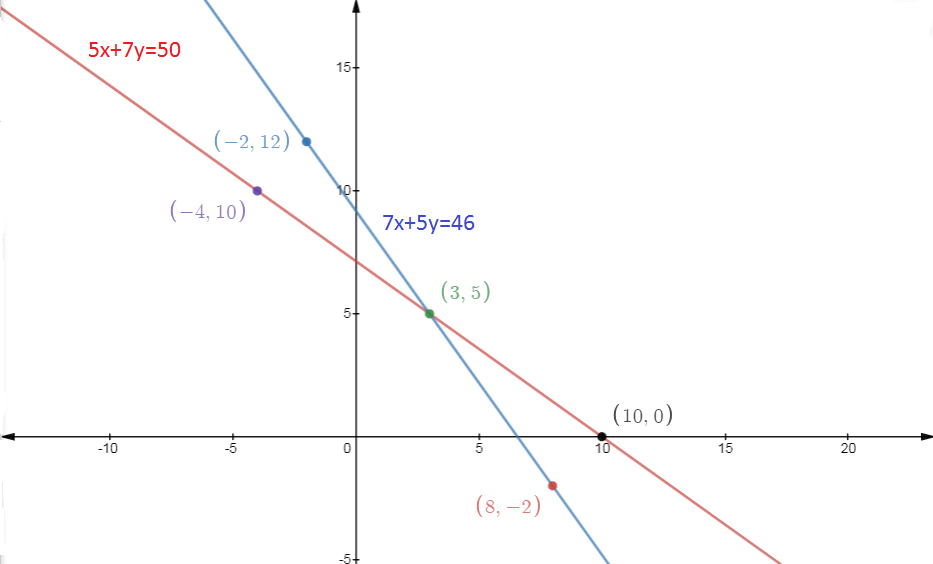
From the graph, both lines intersect at point (3,5), that is, x = 3 and y = 5, which means the cost of 1 pencil is 3 and the cost of 1 pen is 5.

Q2 (i): On comparing the ratios $\frac{a_1}{a_2}$, $\frac{b_1}{b_2}$and $\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (i) $\\5x - 4y + 8 = 0; \\ 7x + 6y - 9 = 0$

Answer:

Given Equations,

$\\5x - 4y + 8 = 0 $and$ 7x + 6y - 9 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\frac{a_1}{a_2}=\frac{5}{7},\:\frac{b_1}{b_2}=\frac{-4}{6}\:and\:\frac{c_1}{c_2}=\frac{8}{-9}$

It is observed that;

$\frac{a_1}{a_2}\neq\frac{b_1}{b_2}$

It means that both lines intersect at exactly one point and have a unique solution.

Q2 (ii): On comparing the ratios $\frac{a_1}{a_2}$, $\frac{b_1}{b_2}$and $\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (ii) $\\9x + 3y + 12 = 0; \\ 18x + 6y + 24 = 0$

Answer:

Given Equations,

$\\9x + 3y + 12 = 0$ and $18x + 6y + 24 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{9}{18}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}\: and \\\:\frac{c_1}{c_2}=\frac{12}{24}=\frac{1}{2}$

It is observed that;

$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

It means that both lines are coincident and have infinitely many solutions.

Q2 (iii): On comparing the ratios $\frac{a_1}{a_2}$, $\frac{b_1}{b_2}$and $\frac{c_1}{c_2}$ , find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (iii) $\\6x - 3y + 10 = 0; \\ 2x - y+ 9 = 0$

Answer:

Given Equations,

$\\6x - 3y + 10 = 0$ and$ 2x - y+ 9 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\frac{a_1}{a_2}=\frac{6}{2}=3,\:\frac{b_1}{b_2}=\frac{-3}{-1}=3\:and\:\frac{c_1}{c_2}=\frac{10}{9}$

It is observed that;

$\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}$

It means that both lines are parallel and thus have no solution.

Q3 (i): On comparing the ratios $\frac{a_1}{a_2}$, $\frac{b_1}{b_2}$and $\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (i) $3x + 2y = 5; 2x - 3y = 7$

Answer:

Given Equations,

$\\3x + 2y = 5$ and $2x - 3y = 7$

Or, $3x + 2y - 5 = 0$ and $ 2x - 3y - 7 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\frac{a_1}{a_2}=\frac{3}{2},\:\frac{b_1}{b_2}=\frac{2}{-3}\:and\:\frac{c_1}{c_2}=\frac{5}{7}$

It is observed that;

$\frac{a_1}{a_2}\neq\frac{b_1}{b_2}$

It means that the given equations have a unique solution and thus the pair of linear equations is consistent.

Q3 (ii): On comparing the ratios $\frac{a_1}{a_2}$, $\frac{b_1}{b_2}$and $\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (ii) $2x - 3y = 8; 4x - 6y = 9$

Answer:

Given Equations,

$\\2x - 3y = 8$ and $4x - 6y = 9$

Or, $\\2x - 3y - 8 = 0$ and $4x - 6y - 9 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-3}{-6}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{8}{9}$

It is observed that;

$\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}$

It means the given equations have no solution, and thus the pair of linear equations is inconsistent.

Q3 (iii): On comparing the ratios $\frac{a_1}{a_2}$, $\frac{b_1}{b_2}$and $\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (iii) $\frac{3}{2}x + \frac{5}{3}y = 7; 9x -10y = 14$

Answer:

Given Equations,

$\\\frac{3}{2}x + \frac{5}{3}y = 7$ and $9x -10y = 14$

Or, $\\\frac{3}{2}x + \frac{5}{3}y - 7 = 0$ and $9x -10y - 14 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{\frac32}{9}=\frac{3}{18}=\frac{1}{6},\\\:\frac{b_1}{b_2}=\frac{\frac53}{-10}=\frac{5}{-30}=-\frac{1}{6}\:and\\\:\frac{c_1}{c_2}=\frac{7}{14}=\frac{1}{2}$

It is observed that;

$\frac{a_1}{a_2}\neq\frac{b_1}{b_2}$

It means the given equations have exactly one solution, and thus the pair of linear equations is consistent.

Q3 (iv): On comparing the ratios $\frac{a_1}{a_2}$, $\frac{b_1}{b_2}$and $\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (iv) $5x - 3y = 11; -10x + 6y =-22$

Answer:

Given Equations,

$5x - 3y = 11$ and $-10x + 6y =-22$

Or, $5x - 3y - 11 = 0$ and $-10x + 6y + 22 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{5}{-10}=-\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-3}{6}=-\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{11}{-22}=-\frac{1}{2}$

It is observed that;

$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

It means the given equations have an infinite number of solutions, and thus a pair of linear equations is consistent.

Q3 (v): On comparing the ratios $\frac{a_1}{a_2}$, $\frac{b_1}{b_2}$and $\frac{c_1}{c_2}$, find out whether the following pair of linear equations are consistent, or inconsistent (v) $\frac{4}{3}x + 2y = 8; 2x + 3y = 12$

Answer:

Given Equations,

$\\\frac{4}{3}x + 2y = 8$ and $2x + 3y = 12$

Or, $\\\frac{4}{3}x + 2y - 8 = 0$ and $2x + 3y - 12 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{\frac43}{2}=\frac{4}{6}=\frac{2}{3},\\\:\frac{b_1}{b_2}=\frac{2}{3}\:\:and\\\:\frac{c_1}{c_2}=\frac{8}{12}=\frac{2}{3}$

It is observed that;

$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

It means the given equations have an infinite number of solutions, and thus a pair of linear equations is consistent.

Q4 (i): Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: $x + y = 5; 2x + 2 y = 10$

Answer:

Given Equations,

$\\x + y = 5$ and $2x + 2 y = 10$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{5}{10}=\frac{1}{2}$

It is observed that;

$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

It means the given equations have an infinite number of solutions, and thus a pair of linear equations is consistent.

The points (x,y) which satisfy both equations are

Q4 (ii): Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: $x - y = 8; 3x - 3y = 16$

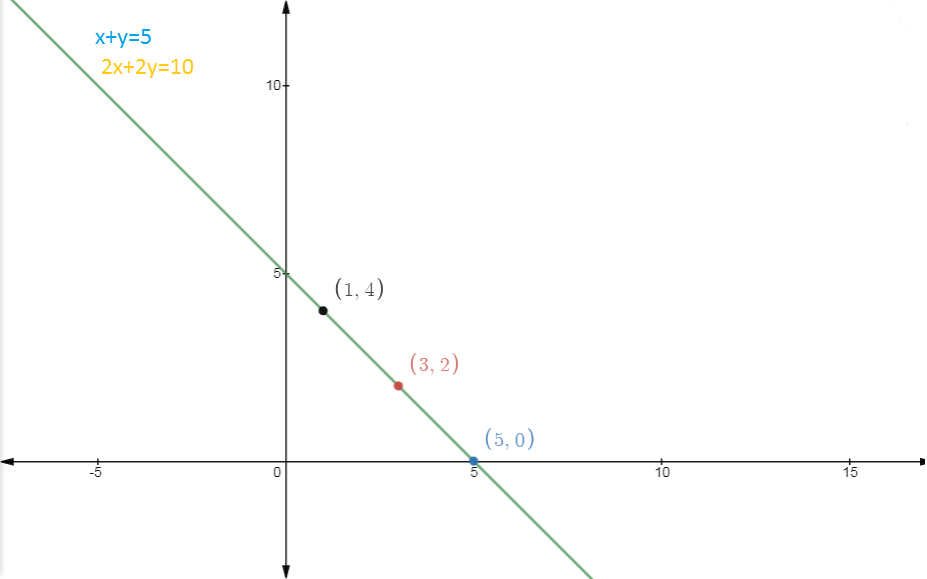
Answer:

Given Equations,

$\\x - y = 8$ and $3x - 3y = 16$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{1}{3},\\\:\frac{b_1}{b_2}=\frac{-1}{-3}=\frac{1}{3}\:and\\\:\frac{c_1}{c_2}=\frac{8}{16}=\frac{1}{2}$

It is observed that:

$\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}$

It means the given equations have no solution, and thus the pair of linear equations is inconsistent.

Q4 (iii): Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: $2x + y - 6 =0; 4x - 2 y - 4 = 0$

Answer:

Given Equations,

$\\2x + y - 6 =0$ and $4x - 2 y - 4 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{1}{-2}=-\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{-6}{-4}=\frac{3}{2}$

It is observed that;

$\frac{a_1}{a_2}\neq\frac{b_1}{b_2}$

It means the given equations have exactly one solution, and thus the pair of linear equations is consistent.

The points(x, y) satisfying the equation $\\2x + y - 6 =0$ are,

And The points(x,y) satisfying the equation $\\4x - 2y - 4 = 0$ are,

GRAPH:

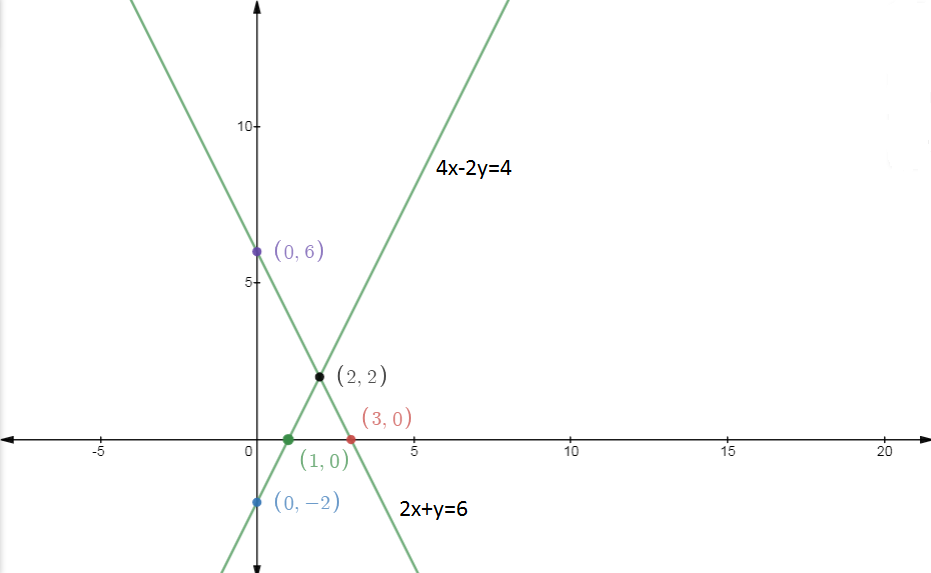
As we can see, both lines intersect at point (2,2) and hence the solution of both equations is x = 2 and y = 2.

Q4 (iv): Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: $2x - 2y - 2 =0; 4x - 4y -5 = 0$

Answer:

Given Equations,

$\\2x - 2y - 2 =0, \qquad\\ 4x - 4y -5 = 0$

Comparing these equations with $a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0$ , we get

$\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-2}{-4}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{-2}{-5}=\frac{2}{5}$

It is observed that;

$\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}$

It means the given equations have no solution, and thus the pair of linear equations is inconsistent.

Q5: Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.

Answer:

Let $ l$ be the length of the rectangular garden and $b$ be the width.

Now, according to the question, the length is 4 m more than its width, so we can write it as $l=b+4$

Or, $l-b=4....(1)$

Also given Half Parameter of the rectangle = 36 it means $l+b=36....(2)$

Now, as we have two equations, add both equations, and we get,

$l+b+l-b=4+36$

$\Rightarrow 2l=40$

$\Rightarrow l=20$

We get the value of $l$, which is 20m

Now, putting this in equation (1), we get;

$\Rightarrow 20-b=4$

$\Rightarrow b=20-4$

$\Rightarrow b=16$

Hence, the Length and width of the rectangle are 20m and 16m, respectively.

Q6 (i): Given the linear equation $2x + 3y -8 =0$, write another linear equation in two variables such that the geometrical representation of the pair so formed is: intersecting lines

Answer:

Given the equation,

$2x + 3y -8 =0$

We know that the condition for the intersection of lines for the equations in the form $ a_1x+b_1y+c_1=0$ and $ a_2x+b_2y+c_2=0$ is,

$\frac{a_1}{a_2}\neq\frac{b_1}{b_2}$

So any line with this condition can be $4x+3y-16=0$

Proof,

$\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}$

$\frac{b_1}{b_2}=\frac{3}{3}=1$

Hence, $\frac{1}{2}\neq1$ it means $\frac{a_1}{a_2}\neq\frac{b_1}{b_2}$

Therefore, the pair of lines has a unique solution, thus forming intersecting lines.

Q6 (ii): Given the linear equation $2x + 3y -8 =0$ , write another linear equation in two variables such that the geometrical representation of the pair so formed is parallel lines

Answer:

Given the equation,

$2x + 3y -8 =0$

As we know, the condition for the parallel lines for the equations in the form $ a_1x+b_1y+c_1=0$ and $ a_2x+b_2y+c_2=0$ is,

$\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}$

So any line with this condition can be $4x+6y-8=0$

Proof,

$\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}$

$\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}$

$\frac{c_1}{c_2}=\frac{-8}{-8}=1$

Hence, $\frac{1}{2}=\frac{1}{2}\neq1$ it means $\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}$

Therefore, the pair of lines has no solutions; thus, the lines are parallel.

Q6 (iii): Given the linear equation $2x + 3y -8 =0$, write another linear equation in two variables such that the geometrical representation of the pair so formed is: coincident lines

Answer:

Given the equation,

$2x + 3y -8 =0$

As we know, the condition for the coincidence of the lines for the equations in the form $ a_1x+b_1y+c_1=0$ and $ a_2x+b_2y+c_2=0$ is,

$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

So any line with this condition can be $4x+6y-16=0$

Proof,

$\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}$

$\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}$

$\frac{c_1}{c_2}=\frac{-8}{-16}=\frac{1}{2}$

Hence, $\frac{1}{2}=\frac{1}{2}=\frac{1}{2}$ it means $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

Therefore, the pair of lines has infinitely many solutions; thus, the lines are coincident.

Q7: Draw the graphs of the equations $x - y + 1=0$and $3x +2 y - 12=0$ . Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.

Answer:

Given two equations,

$x - y + 1=0.........(1)$

And

$3x +2 y - 12=0.........(2)$

The points (x,y) satisfying (1) are

And The points(x,y) satisfying (2) are,

GRAPH:

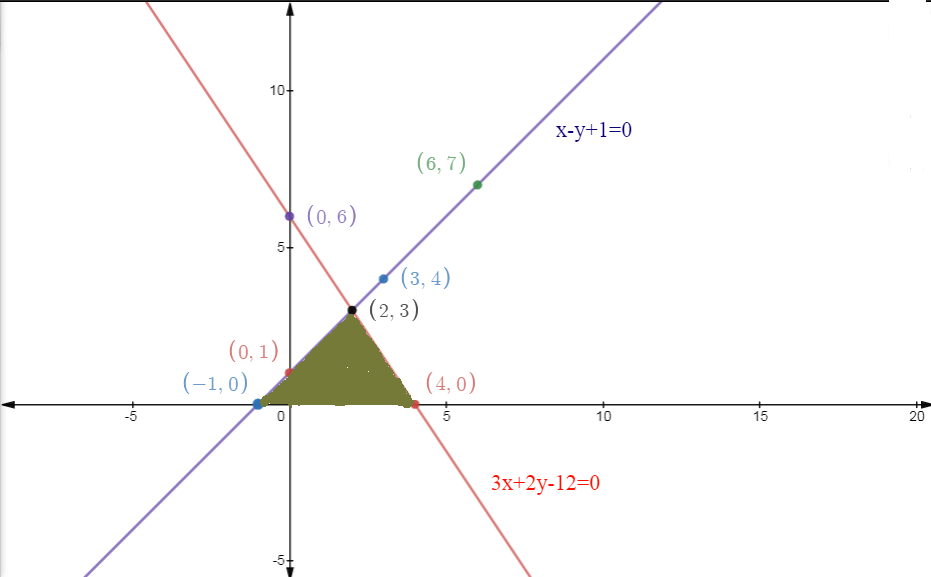
As we can see from the graph that both lines intersect at the point (2,3), And the vertices of the Triangle are ( -1,0), (2,3) and (4,0). The area of the triangle is shaded with a green color.

Q1(i): Solve the following pair of linear equations by the substitution method.

$x+y=14$

$x−y=4$

Answer:

Given two equations,

$x+y=14$.......(1)

$x−y=4$........(2)

Now, from (1), we have

$y=14−x$........(3)

Substituting this in (2), we get

$x−(14−x)=4$

$\Rightarrow x−14+x=4$

$\Rightarrow 2x=4+14=18$

$\Rightarrow x=9$

Substituting this value of x in (3)

$\Rightarrow y=14−x=14−9=5$

Hence, the solution of the given equations is x = 9 and y = 5.

Q1(ii): Solve the following pair of linear equations by the substitution method

$s−t=3$

$\frac{s}{3}+\frac{t}{2}=6$

Answer:

Given two equations,

$s−t=3$..........(1)

$\frac{s}{3}+\frac{t}{2}=6$....... (2)

Now, from (1), we have

$s=t+3$........(3)

Substituting this in (2), we get

$\frac{t+3}{3}+\frac{t}{2}=6$

$\Rightarrow 2t+6+3t=36$

$\Rightarrow 5t+6=36$

$\Rightarrow 5t=30$

$\Rightarrow t=6$

Substituting this value of t in (3)

$\Rightarrow s=t+3=6+3=9$

Hence, the solution of the given equations is s = 9 and t = 6.

Q1(iii): Solve the following pair of linear equations by the substitution method.

$3x−y=39$

$9x−3y=9$

Answer:

Given two equations,

$3x−y=3$......(1)

$9x−3y=9$.....(2)

Now, from (1), we have

$y=3x−3$........(3)

Substituting this in (2), we get

$9x−3(3x−3)=9$

$\Rightarrow 9x−9x+9=9$

$\Rightarrow 9=9$

This is always true, and hence this pair of equations has infinite solutions.

As we have

$y=3x−3$,

One of many possible solutions is x = 1, and y = 0.

Q1(iv): Solve the following pair of linear equations by the substitution method.

$0.2x+0.3y=1.3$

$0.4x+0.5y=2.3$

Answer:

Given two equations,

$0.2x+0.3y=1.3$

$0.4x+0.5y=2.3$

Now, from (1), we have

$y=\frac{1.3−0.2x}{0.3}$........(3)

Substituting this in (2), we get

$0.4x+0.5\frac{1.3−0.2x}{0.3}=2.3$

$\Rightarrow 0.12x+0.65−0.1x=0.69$

$\Rightarrow 0.02x=0.69−0.65=0.04$

$\Rightarrow x=2$

Substituting this value of x in (3)

$\Rightarrow y=\frac{1.3−0.2x}{0.3} =\frac{1.3−0.2 × 2}{0.3} =3$

Hence, the solution of the given equations is

x = 2 and y = 3.

Q1(v): Solve the following pair of linear equations by the substitution method.

$\sqrt 2x+ \sqrt 3y=0$

$\sqrt 3x−\sqrt 8y=0$

Answer:

Given two equations,

$\sqrt 2x+ \sqrt 3y=0$

$\sqrt 3x−\sqrt 8y=0$

Now, from (1), we have

$x=\frac{−\sqrt 3y}{\sqrt 2}$........(3)

Substituting this in (2), we get

$\sqrt 3 (\frac{−\sqrt 3y}{\sqrt 2}) - \sqrt 8y=0$

$\Rightarrow \frac{−\sqrt 3y}{\sqrt 2} - 2\sqrt 2y = 0$

$\Rightarrow y(\frac{−\sqrt 3}{\sqrt 2} - 2\sqrt 2) = 0$

$\Rightarrow y=0$

Substituting this value of y in (3)

$\Rightarrow x = 0$

Hence, the solution of the given equations is,

x = 0, and y = 0 .

Q1(vi): Solve the following pair of linear equations by the substitution method.

$\frac{3x}{2}−\frac{5y}{3} =−2$

$\frac{x}{3}+\frac{y}{2}=\frac{13}{6}$

Answer:

Given,

$\frac{3x}{2}−\frac{5y}{3} =−2$ ....... (1)

$\frac{x}{3}+\frac{y}{2}=\frac{13}{6}$ ........ (2)

From (1) we have,

$x=\frac{(-12 + 10y)}{9}$........(3)

Putting this in (2), we get,

$\frac{\frac{(-12 + 10y)}{9}}{3}+ \frac{y}{2} = \frac{13}{6}$

$\frac{(-12 + 10y)}{27}+ \frac{y}{2} = \frac{13}{6}$

$\frac{(-24 + 20y + 27y)}{54} = \frac{13}{6}$

$47y=141$

$y=3$

Putting this value in (3), we get,

$x=\frac{(-12 + 10× 3)}{9}$

$x =2$

Hence, x = 2 and y = 3.

Q2: Solve 2x + 3y = 11 and 2x − 4y = −24 and hence find the value of ‘m’ for which y = mx + 3.

Answer:

Given two equations,

$2x+3y=11$......(1)

$2x−4y=−24$.......(2)

Now, from (1), we have

$y=\frac{11−2x}{3}$........(3)

Substituting this in (2), we get

$2x−4(\frac{11−2x}{3})=−24$

$\Rightarrow 6x−44+8x=−72$

$\Rightarrow 14x=44−72$

$\Rightarrow 14x=−28$

$\Rightarrow x=−2$

Substituting this value of x in (3)

$\Rightarrow y=\frac{11−2x}{3}=\frac{11−2×(−2)}{3}=\frac{15}{3}=5$

Hence, the solution of the given equations is,

x = −2, and y = 5.

Now,

As it satisfies $y=mx+3$,

$\Rightarrow 5=m(−2)+3$

$\Rightarrow 2m=3−5$

$\Rightarrow 2m=−2$

$\Rightarrow m=−1$

Hence, the value of m is -1.

Q3(i): Form the pair of linear equations for the following problem and find their solution by the substitution method.

The difference between the two numbers is 26, and one number is three times the other. Find them.

Answer:

Let two numbers be x and y, and the bigger number is y.

Now, according to the question,

$y−x=26$......(1)

And

$y=3x$......(2)

Now, substituting the value of y from (2) in (1), we get,

$3x−x=26$

$\Rightarrow 2x=26$

$\Rightarrow x=13$

Substituting this in (2)

$\Rightarrow y=3x=3(13)=39$

Hence, the two numbers are 13 and 39.

Q3(ii): Form the pair of linear equations for the following problem and find their solution by the substitution method

The larger of the two supplementary angles exceeds the smaller by 18 degrees. Find them.

Answer:

Let the larger angle be x and the smaller angle be y

Now, as we know, the sum of supplementary angles is 180. so,

$x+y=180°$.......(1)

Also given in the question,

$x−y=18°$.......(2)

Now, from (2) we have,

$y=x−18°$.......(3)

Substituting this value in (1)

$x+x−18°=180°$

$\Rightarrow 2x=180°+18°$

$\Rightarrow 2x=198°$

$\Rightarrow x=99°$

Now, substituting this value of x in (3), we get

$\Rightarrow y=x−18°=99°−18°=81°$

Hence, the two supplementary angles are

$99°$ and $81°$.

Q3: Form the pair of linear equations for the following problems and find their solution by the substitution method.
(iii) The coach of a cricket team buys 7 bats and 6 balls for Rs 3800. Later, she buys 3 bats and 5 balls for Rs 1750. Find the cost of each bat and each ball.

Answer:

Let the cost of 1 bat is x and the cost of 1 ball is y.

Now, according to the question,

$7x+6y=3800$......(1)

$3x+5y=1750$......(2)

Now, from (1) we have

$y=\frac{(3800−7x)}{6}$........(3)

Substituting this value of y in (2)

$3x+5\frac{(3800−7x)}{6}=1750$

$\Rightarrow 18x+19000−35x=1750×6$

$\Rightarrow −17x=10500−19000$

$\Rightarrow −17x=−8500$

$\Rightarrow x=\frac{8500}{17}$

$\Rightarrow x=500$

Now, Substituting this value of x in (3)

$y=\frac{(3800−7x)}{6}$

$y =\frac{3800−7×500}{6}$

$y =\frac{3800−3500}{6}=50$

Hence, the cost of one bat is 500 Rs and the cost of one ball is 50 Rs.

Q3: Form the pair of linear equations for the following problems and find their solution by the substitution method.
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is Rs 105, and for a journey of 15 km, the charge paid is Rs 155. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of 25 km?

Answer:

Let the fixed charge be x and the per km charge be y.

Now, according to the question

$x+10y=105$.......(1)

And,

$x+15y=155$.......(2)

Now, from (1) we have,

$x=105−10y$........(3)

Substituting this value of x in (2), we have

$105−10y+15y=155$

$\Rightarrow 5y=155−105$

$\Rightarrow 5y=50$

$\Rightarrow y=10$

Now, substituting this value in (3)

$x=105−10y$

$=105−10(10)$

$=105−100=5$

Hence, the fixed charge is 5 Rs and the per km charge is 10 Rs.

Now, Fair for 25 km :

$\Rightarrow x+25y=5+25(10) $

$=5+250=255$

Hence, the fare for 25 km is 255 Rs.

Q3:.Form the pair of linear equations for the following problems and find their solution by the substitution method.
(v) A fraction becomes $\frac9{11}$, if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator, it becomes 56. Find the fraction.

Answer:

Let the numerator of the fraction be x, and the denominator of the fraction be y

Now, according to the question,

$\frac{x+2}{y+2}=\frac{9}{11}$

$\Rightarrow 11(x+2)=9(y+2)$

$\Rightarrow 11x+22=9y+18$

$\Rightarrow 11x−9y=−4$.........(1)

Also,

$\frac{x+3}{y+3}=\frac{5}{6}$

$\Rightarrow 6(x+3)=5(y+3)$

$\Rightarrow 6x+18=5y+15$

$\Rightarrow 6x−5y=−3$...........(2)

Now, from (1) we have

$y=\frac{11x+4}{9}$.............(3)

Substituting this value of y in (2)

$6x−5(\frac{11x+4}{9})=−3$

$\Rightarrow 54x−55x−20=−27$

$\Rightarrow −x=20−27$

$\Rightarrow x=7$

Substituting this value of x in (3)

$y={11x+4}{9}$

$=\frac{11(7)+4}{9}=\frac{81}{9}=9$

Hence, the required fraction is

$x =\frac{7}{9}$

Q3: Form the pair of linear equations for the following problems and find their solution by the substitution method.
(vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?

Answer:

Let x be the age of Jacob and y be the age of Jacob's son.

Now, according to the question

$x+5=3(y+5)$

$\Rightarrow x+5=3y+15$

$\Rightarrow x−3y=10$........(1)

Also,

$x−5=7(y−5)$

$\Rightarrow x−5=7y−35$

$\Rightarrow x−7y=−30$.........(2)

Now,

From (1) we have,

$x=10+3y$...........(3)

Substituting this value of x in (2)

$10+3y−7y=−30$

$\Rightarrow −4y=−30−10$

$\Rightarrow 4y=40$

$\Rightarrow y=10$

Substituting this value of y in (3),

$x=10+3y=10+3(10)=10+30=40$

Hence, the present age of Jacob is 40 years, and the present age of Jacob's son is 10 years.

Q1(i): Solve the following pair of linear equations by the elimination method and the substitution method :

$x + y =5 \ \textup{and} \ 2x - 3y = 4$

Answer:

Elimination Method:

Given, equations

$\\x + y =5............(1) \ \textup{and} \\ \ 2x - 3y = 4........(2)$

Now, multiplying (1) by 3, we get

$\\3x +3 y =15............(3)$

Now, adding (2) and (3), we get

$\\2x-3y+3x +3 y =4+15$

$\Rightarrow 5x=19$

$\Rightarrow x=\frac{19}{5}$

Substituting this value in (1), we get

$\frac{19}{5}+y=5$

$\Rightarrow y=5-\frac{19}{5}$

$\Rightarrow y=\frac{6}{5}$

Hence,

$x=\frac{19}{5}\:and\:y=\frac{6}{5}$

Substitution method :

Given, equations

$\\x + y =5............(1) \ \textup{and} \\ \ 2x - 3y = 4........(2)$

Now, from (1) we have,

$y=5-x.......(3)$

Substituting this value in (2)

$2x-3(5-x)=4$

$\Rightarrow 2x-15+3x=4$

$\Rightarrow 5x=19$

$\Rightarrow x=\frac{19}{5}$

Substituting this value of x in (3)

$\Rightarrow y=5-x=5-\frac{19}{5}=\frac{6}{5}$

Hence,

$x=\frac{19}{5}\:and\:y=\frac{6}{5}$

Q1(ii): Solve the following pair of linear equations by the elimination method and the substitution method :

$3x + 4 y = 10 \ \textup{and} \ 2x - 2y = 2$

Answer:

Elimination Method:

Given, equations

$\\3x + 4 y = 10............(1) \ \textup{and}\\ \ 2x - 2y = 2..............(2)$

Now, multiplying (2) by 2, we get

$\\4x -4 y =4............(3)$

Now, adding (1) and (3), we get

$\\3x+4y+4x -4 y =10+4$

$\Rightarrow 7x=14$

$\Rightarrow x=2$

Putting this value in (2), we get

$2(2)-2y=2$

$\Rightarrow 2y=2$

$\Rightarrow y=1$

Hence,

$x=2\:and\:y=1$

Substitution method :

Given, equations

$\\3x + 4 y = 10............(1) \ \textup{and}\\ \ 2x - 2y = 2..............(2)$

Now, from (2) we have,

$y=\frac{2x-2}{2}=x-1.......(3)$

Substituting this value in (1)

$3x+4(x-1)=10$

$\Rightarrow 3x+4x-4=10$

$\Rightarrow 7x=14$

$\Rightarrow x=2$

Substituting this value of x in (3)

$\Rightarrow y=x-1=2-1=1$

Hence, $x=2\:and\:y=1$

Q1(iii): Solve the following pair of linear equations by the elimination method and the substitution method: (iii) $3x - 5y -4 = 0\ \textup{and} \ 9x = 2y + 7$

Answer:

Elimination Method:

Given, equations

$\\3x - 5y -4 = 0..........(1)\ \textup{and}\ \\9x = 2y + 7$

$\\\Rightarrow 9x - 2y -7=0........(2)$

Now, multiplying (1) by 3, we get

$\\9x -15 y -12=0............(3)$

Now, subtracting (3) from (2), we get

$9x-2y-7-9x+15y+12=0$

$\Rightarrow 13y+5=0$

$\Rightarrow y=\frac{-5}{13}$

Putting this value in (1), we get

$3x-5(\frac{-5}{13})-4=0$

$\Rightarrow 3x=4-\frac{25}{13}$

$\Rightarrow 3x=\frac{27}{13}$

$\Rightarrow x=\frac{9}{13}$

Hence,

$x=\frac{9}{13}\:and\:y=-\frac{5}{13}$

Substitution method :

Given, equations

$\\3x - 5y -4 = 0..........(1)\ \textup{and}\ \\9x = 2y + 7$

$\\\Rightarrow 9x - 2y -7=0........(2)$

Now, from (2) we have,

$y=\frac{9x-7}{2}.......(3)$

Substituting this value in (1)

$3x-5\left(\frac{9x-7}{2} \right )-4=0$

$\Rightarrow 6x-45x+35-8=0$

$\Rightarrow -39x+27=0$

$\Rightarrow x=\frac{27}{39}=\frac{9}{13}$

Substituting this value of x in (3)

$\Rightarrow y=\frac{9(9/13)-7}{2}=\frac{81/13-7}{2}=\frac{-5}{13}$

Hence, $x=\frac{9}{13}\:and\:y=-\frac{5}{13}$

Q1(iv): Solve the following pair of linear equations by the elimination method and the substitution method :(iv) $\frac{x}{2} + \frac{2y}{3} = -1\ \textup{and} \ x - \frac{y}{3} = 3$

Answer:

Elimination Method:

Given, equations

$\\\frac{x}{2} + \frac{2y}{3} = -1........(1)\ \textup{and} \ \\ \\x - \frac{y}{3} = 3............(2)$

Now, multiplying (2) by 2, we get

$\\2x - \frac{2y}{3} =6............(3)$

Now, adding (1) and (3), we get

$\\\frac{x}{2}+\frac{2y}{3}+2x-\frac{2y}{3}=-1+6$

$\Rightarrow \frac{5x}{2}=5$

$\Rightarrow x=2$

Putting this value in (2), we get

$2-\frac{y}{3}=3$

$\Rightarrow \frac{y}{3}=-1$

$\Rightarrow y=-3$

Hence,

$x=2\:and\:y=-3$

Substitution method :

Given, equations

$\\\frac{x}{2} + \frac{2y}{3} = -1........(1)\ \textup{and} \ \\ \\x - \frac{y}{3} = 3............(2)$

Now, from (2) we have,

$y=3(x-3)......(3)$

Substituting this value in (1)

$\frac{x}{2}+\frac{2(3(x-3))}{3}=-1$

$\Rightarrow \frac{x}{2}+2x-6=-1$

$\Rightarrow \frac{5x}{2}=5$

$\Rightarrow x=2$

Substituting this value of x in (3)

$\Rightarrow y=3(x-3)=3(2-1)=-3$

Hence, $x=2\:and\:y=-3$

Q2(i): Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method : (i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes $\frac{1}{2 }$ if we only add 1 to the denominator. What is the fraction?

Answer:

Let the numerator of the fraction be x, and the denominator is y,

Now, according to the question,

$\frac{x+1}{y-1}=1$

$\Rightarrow x+1=y-1$

$\Rightarrow x-y=-2.........(1)$

Also,

$\frac{x}{y+1}=\frac{1}{2}$

$\Rightarrow 2x=y+1$

$\Rightarrow 2x-y=1..........(2)$

Now, subtracting (1) from (2), we get

$x=3$

Putting this value in (1)

$3-y=-2$

$\Rightarrow y=5$

Hence, $x=3\:and\:y=5$

And the fraction is: $\frac{3}{5}$

Q2(ii): Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method : (ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?

Answer:

Let the age of Nuri be x and the age of Sonu be y.

Now, according to the question

$x-5=3(y-5)$

$\Rightarrow x-5=3y-15$

$\Rightarrow x-3y=-10.........(1)$

Also,

$x+10=2 (y+10)$

$\Rightarrow x+10=2y+20$

$\Rightarrow x-2y=10........(2)$

Now, subtracting (1) from (2), we get

$y=20$

Putting this value in (2)

$x-2(20)=10$

$\Rightarrow x=50$

Hence, the age of Nuri is 50 and the age of Nuri is 20.

Q2(iii): Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method : (iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.

Answer:

Let the unit digit of the number be x and the 10's digit be y.

Now, according to the question,

$x+y=9.......(1)$

Also

$9(10y+x)=2(10x+y)$

$\Rightarrow 90y+9x=20x+2y$

$\Rightarrow 88y-11x=0$

$\Rightarrow 8y-x=0.........(2)$

Now adding (1) and (2), we get,

$\Rightarrow 9y=9$

$\Rightarrow y=1$

Now putting this value in (1)

$x+1=9$

$\Rightarrow x=8$

Hence, the number is 18.

Q2(iv): Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method : (iv) Meena went to a bank to withdraw Rs 2000. She asked the cashier to give her Rs 50 and Rs 100 notes only. Meena got 25 notes in all. Find how many notes of Rs 50 and Rs 100 she received.

Answer:

Let the number of Rs 50 notes be x and the number of Rs 100 notes be y.

Now, according to the question,

$x+y=25..........(1)$

And

$50x+100y=2000$

$\Rightarrow x+2y=40.............(2)$

Now, subtracting (1) from (2), we get

$y=15$

Putting this value in (1).

$x+15=25$

$\Rightarrow x=10$

Hence, Meena received 10, 50 Rs notes and 15, 100 Rs notes.

Q2(v): Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method : (v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs 27 for a book kept for seven days, while Susy paid Rs 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.

Answer:

Let the fixed charge be x, and per day charge is y.

Now, according to the question,

$x+4y=27...........(1)$

And

$x+2y=21...........(2)$

Now, Subtracting (2) from (1). We get,

$4y-2y=27-21$

$\Rightarrow 2y=6$

$\Rightarrow y=3$

Putting this in (1)

$x+4(3)=27$

$\Rightarrow x=27-12=15$

Hence, the fixed charge is 15 Rs and the per-day charge is 3 Rs.