NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials: Free PDF Download

Careers360 brings you NCERT Class 10 Maths Chapter 2 Polynomials solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.

Download PDF

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials: Exercise Questions

Below, you will find the NCERT Class 10 Maths Chapter 2 Polynomials question answers explained step by step.

Q1 (1): The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the numbers of zeroes of p(x), in each case.

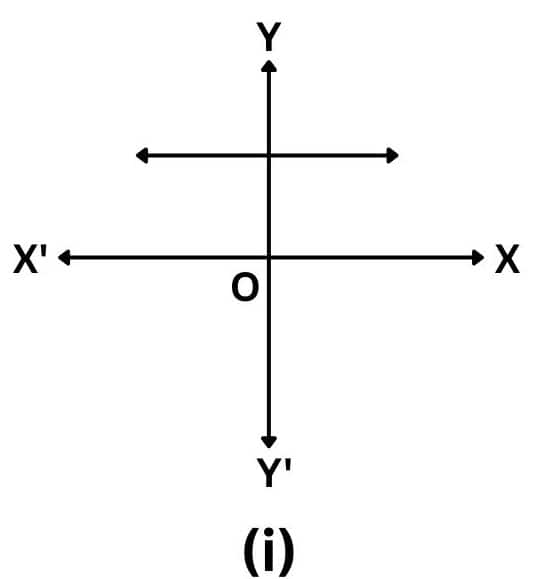
Answer: The number of zeroes of p(x) is zero, as the curve does not intersect the x-axis.

Q1 (2): The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

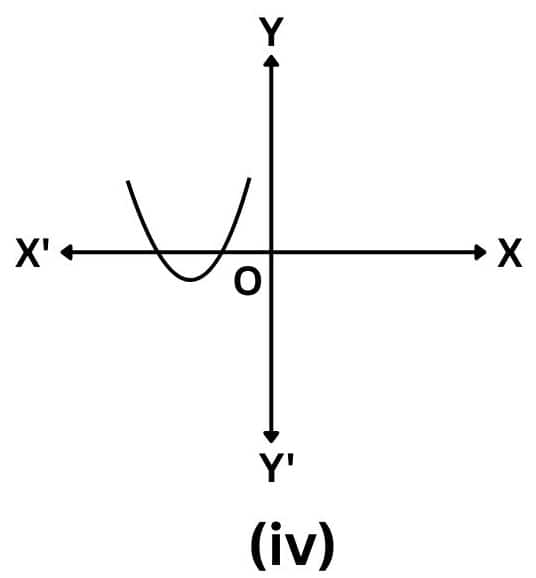
Answer: The number of zeroes of p(x) is one, as the curve intersects the x-axis only once.

Q1 (3): The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

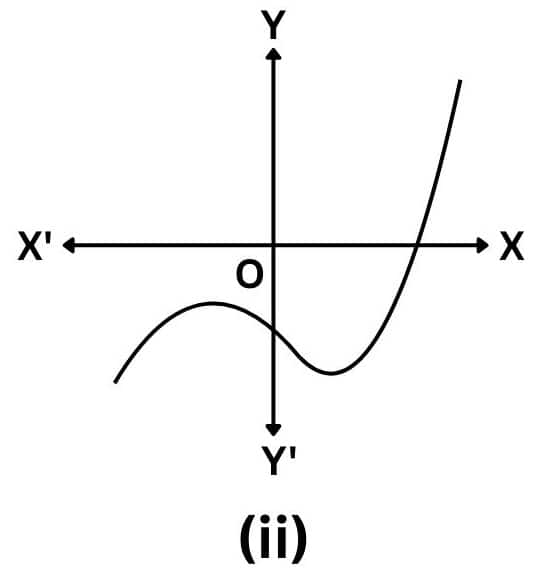
Answer: The number of zeroes of p(x) is three as the graph intersects the x-axis thrice.

Q1 (4): The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

Answer: The number of zeroes of p(x) is two, as the graph intersects the x-axis twice.

Q1 (5): The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

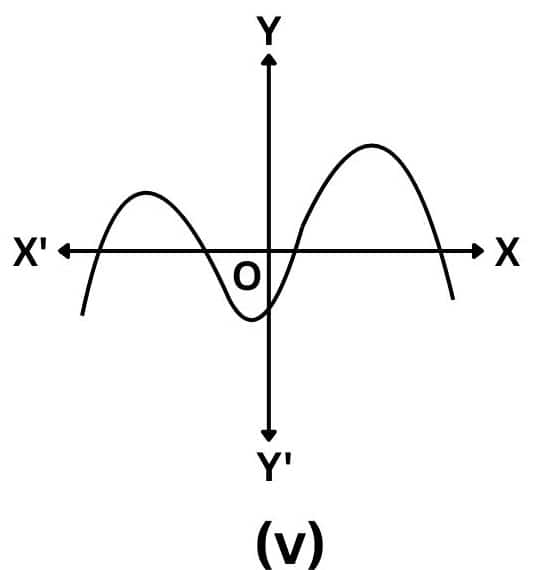
Answer: The number of zeroes of p(x) is four, as the graph intersects the x-axis four times.

Q1 (6): The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x) in each case

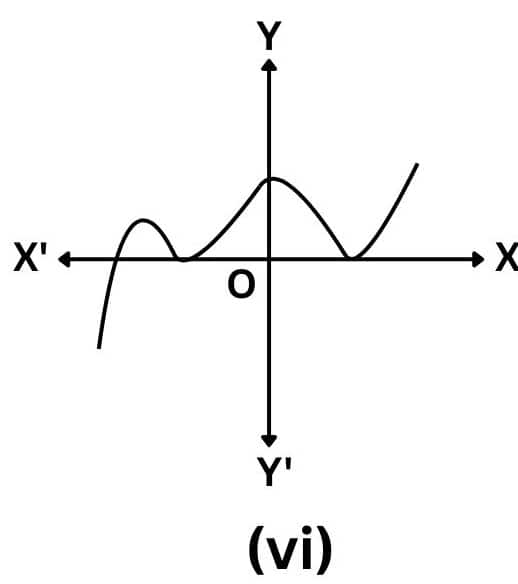
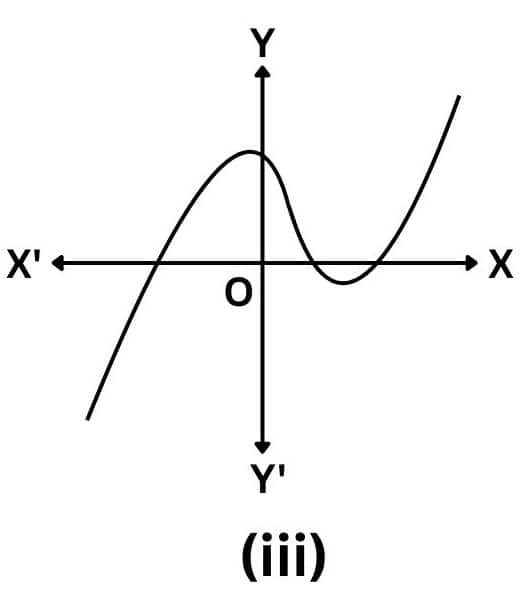
Answer: The number of zeroes of p(x) is three as the graph intersects the x-axis thrice.

Q1 (i): Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. $x^2-2 x-8$

Answer:

x² - 2x - 8 = 0

x² - 4x + 2x - 8 = 0

x(x-4) +2(x-4) = 0

(x+2)(x-4) = 0

The zeroes of the given quadratic polynomial are -2 and 4

$\\\alpha =-2\\, \beta =4$

VERIFICATION:

Sum of roots:

$
\begin{aligned}
& \alpha+\beta=-2+4=2 \\
& -\frac{\text { coefficient of } x}{\text { coefficient of } x^2} \\
& =-\frac{-2}{1} \\
& =2 \\
& =\alpha+\beta
\end{aligned}
$

Verified
Product of roots:

$
\begin{aligned}
& \alpha \beta=-2 \times 4=-8 \\
& \frac{\text { constant term }}{\text { coefficient of } x^2} \\
& =\frac{-8}{1} \\
& =-8 \\
& =\alpha \beta
\end{aligned}
$

Verified

Q1 (ii): Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. $4 s^2-4 s+1$

Answer:

$
\begin{aligned}
& 4 s^2-4 s+1=0 \\
& 4 s^2-2 s-2 s+1=0 \\
& 2 s(2 s-1)-1(2 s-1)=0 \\
& (2 s-1)(2 s-1)=0
\end{aligned}
$
The zeroes of the given quadratic polynomial are $1 / 2$ and $1 / 2$

$
\begin{aligned}
& \alpha=\frac{1}{2} \\
& \beta=\frac{1}{2}
\end{aligned}
$
VERIFICATION
Sum of roots:

$
\alpha+\beta=\frac{1}{2}+\frac{1}{2}=1
$

$
\begin{aligned}
& -\frac{\text { coefficient of } x}{\text { coefficient of } x^2} \\
& =-\frac{-4}{4} \\
& =1 \\
& =\alpha+\beta
\end{aligned}
$
Verified
Product of roots:

$
\begin{aligned}
& \alpha \beta=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4} \\
& \frac{\text { constant term }}{\text { coefficient of } x^2} \\
& =\frac{1}{4} \\
& =\alpha \beta
\end{aligned}
$

Verified

Q1 (iii): Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. $6 x^2-3-7 x$

Answer:

6x² - 3 - 7x = 0

6x² - 7x - 3 = 0

6x² - 9x + 2x - 3 = 0

3x(2x - 3) + 1(2x - 3) = 0

(3x + 1)(2x - 3) = 0

The zeroes of the given quadratic polynomial are -1/3 and 3/2

$
\begin{aligned}
& \alpha=-\frac{1}{3} \\
& \beta=\frac{3}{2}
\end{aligned}
$
Sum of roots:

$
\begin{aligned}
& \alpha+\beta=-\frac{1}{3}+\frac{3}{2}=\frac{7}{6} \\
& -\frac{\text { coefficient of } x}{\text { coefficient of } x^2} \\
& =-\frac{-7}{6} \\
& =\frac{7}{6} \\
& =\alpha+\beta
\end{aligned}
$

Verified

Product of roots:

$\begin{aligned} & \alpha \beta=-\frac{1}{3} \times \frac{3}{2}=-\frac{1}{2} \\ & \frac{\text { constant term }}{\text { coefficient of } x^2} \\ & =\frac{-3}{6} \\ & =-\frac{1}{2} \\ & =\alpha \beta\end{aligned}$

Verified

Q1 (iv): Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. $4 u^2+8 u$

Answer:
4u² + 8u = 0

4u(u + 2) = 0

The zeroes of the given quadratic polynomial are 0 and -2

$
\begin{aligned}
& \alpha=0 \\
& \beta=-2
\end{aligned}
$
VERIFICATION:
Sum of roots:

$
\begin{aligned}
& \alpha+\beta=0+(-2)=-2 \\
& -\frac{\text { coefficient of } x}{\text { coefficient of } x^2} \\
& =-\frac{8}{4} \\
& =-2 \\
& =\alpha+\beta
\end{aligned}
$

Verified
Product of roots:

$
\alpha \beta=0 \times-2=0
$

$\begin{aligned} & \frac{\text { constant term }}{\text { coeff ficient of } x^2} \\ & =\frac{0}{4} \\ & =0 \\ & =\alpha \beta\end{aligned}$

Verified

Q1 (v): Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. $t^2-15$

Answer:
t² - 15 = 0

$
(t-\sqrt{15})(t+\sqrt{15})=0
$

The zeroes of the given quadratic polynomial are $-\sqrt{15}$ and $\sqrt{15}$

$
\begin{aligned}
& \alpha=-\sqrt{15} \\
& \beta=\sqrt{15}
\end{aligned}
$
VERIFICATION:
Sum of roots:

$
\begin{aligned}
& \alpha+\beta=-\sqrt{15}+\sqrt{15}=0 \\
& -\frac{\text { coefficient of } x}{\text { coefficient of } x^2} \\
& =-\frac{0}{1} \\
& =0 \\
& =\alpha+\beta
\end{aligned}
$

Verified

Product of roots:

$\begin{aligned} & \alpha \beta=-\sqrt{15} \times \sqrt{15}=-15 \\ & \frac{\text { constant term }}{\text { coefficient of } x^2} \\ & =\frac{-15}{1} \\ & =-15 \\ & =\alpha \beta\end{aligned}$

Verified

Q1 (vi): Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. $3 x^2-x-4$

Answer:
3x² - x - 4 = 0

3x² + 3x - 4x - 4 = 0

3x(x + 1) - 4(x + 1) = 0

(3x - 4)(x + 1) = 0

The zeroes of the given quadratic polynomial are 4/3 and -1

$
\begin{aligned}
& \alpha=\frac{4}{3} \\
& \beta=-1
\end{aligned}
$
VERIFICATION:
Sum of roots:

$
\begin{aligned}
& \alpha+\beta=\frac{4}{3}+(-1)=\frac{1}{3} \\
& -\frac{\text { coefficient of } x}{\text { coefficient of } x^2} \\
& =-\frac{-1}{3} \\
& =\frac{1}{3} \\
& =\alpha+\beta
\end{aligned}
$

Verified

Product of roots:

$\begin{aligned} & \alpha \beta=\frac{4}{3} \times-1=-\frac{4}{3} \\ & \frac{\text { constant term }}{\text { coefficient of } x^2} \\ & =\frac{-4}{3} \\ & =\alpha \beta\end{aligned}$

Verified

Q2 (i): Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. 1/4 , -1

Answer:

$
\begin{aligned}
& \alpha+\beta=\frac{1}{4} \\
& \alpha \beta=-1
\end{aligned}
$
The required quadratic polynomial is

$
\begin{aligned}
& x^2-(\alpha+\beta)x+\alpha \beta=0 \\
& x^2-\frac{1}{4} x-1=0 \\
& 4 x^2-x-4=0
\end{aligned}
$

Q2 (ii): Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. $\sqrt{2}, 1 / 3$

Answer:

$
\begin{aligned}
& \alpha+\beta=\sqrt{2} \\
& \alpha \beta=\frac{1}{3} \\
& x^2-(\alpha+\beta)x+\alpha \beta=0 \\
& x^2-\sqrt{2} x+\frac{1}{3}=0 \\
& 3 x^2-3 \sqrt{2} x+1=0
\end{aligned}
$
The required quadratic polynomial is $3 x^2-3 \sqrt{2} x+1$

Q2 (iii): Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. $0, \sqrt{5}$

Answer:

$\begin{aligned} & \alpha+\beta=0 \\ & \alpha \beta=\sqrt{5} \\ & x^2-(\alpha+\beta)x+\alpha \beta=0 \\ & x^2-0 x+\sqrt{5}=0 \\ & x^2+\sqrt{5}=0\end{aligned}$

The required quadratic polynomial is x ² + $\sqrt{5}$ .

Q2 (iv): Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. 1,1

Answer:

$\begin{aligned} & \alpha+\beta=1 \\ & \alpha \beta=1 \\ & x^2-(\alpha+\beta)x+\alpha \beta=0 \\ & x^2-1 x+1=0 \\ & x^2-x+1=0\end{aligned}$

The required quadratic polynomial is x² - x + 1

Q2 (v): Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. $-\frac{1}{4}, \frac{1}{4}$

Answer:

$\begin{aligned} & \alpha+\beta=-\frac{1}{4} \\ & \alpha \beta=\frac{1}{4} \\ & x^2-(\alpha+\beta)x+\alpha \beta=0 \\ & x^2-\left(-\frac{1}{4}\right) x+\frac{1}{4}=0 \\ & 4 x^2+x+1=0\end{aligned}$

The required quadratic polynomial is 4x² + x + 1

Q2 (vi): Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. 4,1

Answer:

$\begin{aligned} & \alpha+\beta=4 \\ & \alpha \beta=1 \\ & x^2-(\alpha+\beta)x+\alpha \beta=0 \\ & x^2-4 x+1=0\end{aligned}$

The required quadratic polynomial is x² - 4x + 1.

Polynomials Class 10 Solutions - Exercise Wise

Exercise-wise NCERT Solutions of Polynomials Class 10 Maths Chapter 2 are provided in the links below.

• Polynomials Class 10 Exercise 2.1
• Polynomials Class 10 Exercise 2.2

Polynomials Class 10 Chapter 2: Topics

Topics you will learn in NCERT Class 10 Maths Chapter 2 Polynomials include:

• 2.1 Introduction
• 2.2 Geometrical Meaning of the Zeros of a Polynomial
• 2.3 Relationship between Zeros and Coefficients of a Polynomial

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials: Important Formulae

Polynomials

A polynomial $p(x)$ is an algebraic expression that can be written in the form of

$
p(x)=a_n x^n+\ldots+a_2 x^2+a_1 x+a_0
$

Here $a_0, a_1, a_2, \ldots, a_n$ are real numbers and each power of x is a non-negative integer.

Each real number a_i is called a coefficient. The number a₀  that is not multiplied by a variable is called a constant. Each product  $a_i x_i$  is a term of a polynomial. The highest power of the variable that occurs in the polynomial is called the degree of the polynomial. The leading term is the term with the highest power, and its coefficient is called the leading coefficient.

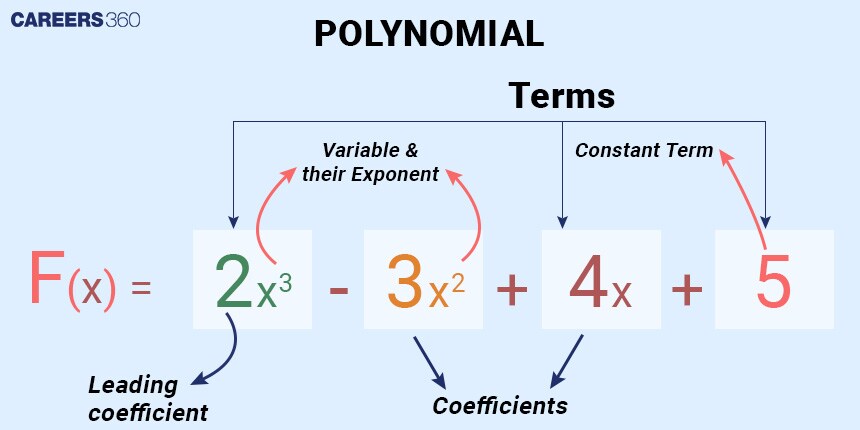
Types of Polynomials

The types of polynomials based on the number of terms are:

• Monomial: A monomial is a polynomial with one term. E.g. $3x$
• Binomial: A binomial is a polynomial with two terms. E.g. $3x+2y$
• Trinomial: A trinomial is a polynomial with three terms. Eg. $4x^2+ 3x+2y$
• Multinomial: A general term for polynomials with more than three terms. Eg. $7x^5+ 5x^3+3x^2+2x=1$
• Constant Polynomial: A constant polynomial is a polynomial with no variable terms but with only a constant term. Eg. $P(x) = 5$
• Zero Polynomial: A polynomial with coefficients as zero. Eg. $0x^2+0x, 0$

Types of polynomials (based on the degree of a polynomial)

• Linear Polynomial: A polynomial with degree one. Eg. $3x+5y = 5$
• Quadratic Polynomial: A Polynomial with degree two. any quadratic polynomial in $x$ is of the form $ax^2 + bx + c$, where $a, b, c$ are real numbers and $a \neq 0$. E.g. $2x^2+3x+2=0$
• Cubic Polynomial: A Polynomial with degree three. The general form of a cubic polynomial is $ax^3 + bx^2 + cx + d$, where $a, b, c, d$ are real numbers and $a \neq 0 $. E.g. $5x^3+3x^2+2x=1$
• Higher-degree polynomial: Polynomials with a degree of more than three. E.g. $7x^5+5x^3+3$

Zeros of a Polynomial

If a real number $k$ satisfies the given polynomial, then $k$ is a zero of that polynomial. (i.e) A real number k is the zero of the polynomial $P(x)$, if $P(k) = 0$

Example: Let $P(x) = x^2 -4$. Let $x = 2$, then $P(x) = 2^2 -4 = 4-4=0$. Therefore, $2$ is the zero of the polynomial $P(x)$.

Graphical Representation of Zeros of a Polynomial

For a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis at most n points. Therefore, a polynomial p(x) of degree n has at most n zeroes.

The number of zeros of a polynomial can be found by the number of points of the graph of the polynomial intersecting the x-axis.

Relationship Between Zeros and Coefficients of the Polynomial

Linear Polynomial:

The zero of the linear polynomial $ax+b$ = $-\frac{b}{a}$.

Quadratic Polynomial:

For the quadratic polynomial $ax^2+bx+c=0$ with zeros $x_1$ and $x_2$,

Sum of zeros, $x_1+x_2= -\frac{b}{a}$

Product of zeros $x_1 x_2= \frac{c}{a}$

Cubic Polynomial:

For the quadratic polynomial $ax^3+bx^2+cx+d=0$ with zeros $x_1$, $x_2$ and $x_3$,

Sum of zeros, $x_1+x_2= -\frac{b}{a}$

Sum of product of two zeros, $x_1 x_2+x_2 x_3+x_3 x_1= \frac{c}{a}$

Product of zeros $x_1 x_2= -\frac{d}{a}$

Why are Class 10 Maths Chapter 2 Polynomials question answers important?

Polynomials are an important part of algebra and help in solving different kinds of equations. This chapter teaches us how to find the zeros of a polynomial and how they relate to its coefficients. These Class 10 Maths Chapter 2 Polynomials question answers help students understand these ideas through simple steps and examples. Here are some points about why these question answers are important:

• These solutions help you learn how to find and use the zeros of a polynomial in different problems.
• These question answers make it easier to understand the link between zeros and coefficients of a polynomial.
• These Class 10 Maths Chapter 2 Polynomials question answers prepare us for higher classes where we will study advanced algebra, functions, and graphs.

NCERT Solutions for Class 10 Maths Chapter Wise

We at Careers360 compiled all the NCERT class 10 Maths solutions in one place for easy student reference. The following links will allow you to access them.

Also, read,

• NCERT Notes Class 10 Maths Chapter 2 Polynomials
• NCERT Exemplar Solutions Class 10 Maths Chapter 2 Polynomials

NCERT Exemplar Solutions Subject-wise

After completing the NCERT textbooks, students should practice exemplar exercises for a better understanding of the chapters and clarity. The following links will help students find exemplar exercises.

• NCERT Exemplar Solutions Class 10th Maths
• NCERT Exemplar Solutions Class 10th Science

NCERT Books and NCERT Syllabus

Here are some useful links for NCERT books and the NCERT syllabus for class 10:

• NCERT Books Class 10 Maths
• NCERT Syllabus Class 10 Maths
• NCERT Books Class 10
• NCERT Books for Class 10 Science
• NCERT Books for Class 10 English
• NCERT Syllabus Class 10