NCERT Solutions for Class 10 Maths Chapter 6 Triangles

We see some clothes hangers, sandwiches, traffic signboards, etc. Do you know which shape they represent? All these things are triangular. Let’s try to find out what a triangle is. Triangles are fundamental geometric 2-D shapes characterized by three sides, three angles, and a sum of 180 degrees for their interior angles. It is the polygon with the least number of sides. The sum of the lengths of the two sides of a triangle is greater than the length of the third side. In the same way, the difference between the two sides of a triangle is less than the length of the third side.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

Don't Miss: JEE Main & NEET 2026 Scholarship Test (Class 10): Narayana | Aakash

Suggested: Important Maths Formulas for Class 10 Maths CBSE

This Story also Contains

1. NCERT Solutions for Class 10 Maths Chapter 6 Triangles PDF Free Download
2. NCERT Class 10 triangle solution- Important Notes
3. NCERT Solutions for Class 10 Maths Chapter 6 Triangles (Exercise)
4. NCERT Solutions Of Class 10 - Subject Wise
5. NCERT Books and NCERT Syllabus
6. NCERT Exemplar Solutions - Subject Wise

This article on NCERT Solutions for Class 10 Maths Chapter 6 Triangles provides clear and step-by-step solutions for exercise problems in the NCERT Class 10 Maths Book. These solutions for class 10 maths chapter 6 Triangles are designed by Subject Matter Experts according to the latest CBSE syllabus, ensuring that students grasp the concepts effectively.

NCERT Solutions for Class 10 Maths Chapter 6 Triangles PDF Free Download

Download PDF

Types of Triangles:

Based on the sides, we have 3 triangles:

• Equilateral Triangles: Triangles that have all 3 sides equal also all the interior angles equal then it is known as equilateral triangles.
• Isosceles Triangle: Triangles that have only two sides equal in length also have angles opposite to the equal side that are equal. It is known as the Isosceles Triangle.
• Scalene Triangle: Triangles that don’t have any equal sides or angles are called scalene triangles.

Based on the measurement of the angle, we have 3 triangles:

• Acute Angle Triangle: Triangles that have all the angles measuring less than 90 degrees is called the Acute Angle Triangle.
• Right Angle Triangle: Triangles that have one angle measuring 90 degrees are called Right Angled Triangles.
• Obtuse Angle Triangle: Triangles that have one angle measuring more than 90 degrees and other angles less than 90 degrees are called Obtuse Angle Triangles.

Similarity Of Triangle:

Two triangles are similar if they have the same ratio of corresponding sides and an equal pair of corresponding angles.

Criteria for Triangle Similarity:

• Angle-Angle-Angle (AAA) Similarity: If the three angles of one triangle are equal to the three angles of another triangle, the triangles are similar.
• Side-Angle-Side (SAS) Similarity: If one angle of a triangle is equal to one angle of another triangle and the two sides including these angles are in the same ratio, then the triangles are similar.
• Side-Side-Side (SSS) Similarity: If the corresponding sides of two triangles are in the same ratio, then the triangles are similar.
• Right Angle-Hypotenuse-Side(RHS) Similarity: If in two right-angled triangles, the hypotenuse and one corresponding side are in the same ratio, then the two triangles are similar.

Important Theorem's

Theorem 6.1: If a line is drawn parallel to one side of a triangle and it cuts the other two sides at different points, it divides those two sides in the same ratio.

Theorem 6.2: If a line divides two sides of a triangle in the same ratio, then the line is parallel to the third side of the triangle.

Theorem 6.3: If two triangles have their corresponding angles equal, then their corresponding sides are in the same ratio, which means the two triangles are similar.

Theorem 6.4: If the sides of one triangle are in the same ratio as the sides of another triangle, then their corresponding angles are also equal, making the two triangles similar.

Theorem 6.5: If one angle of a triangle is equal to one angle of another triangle and the sides around these angles are in the same ratio, then the two triangles are similar.

NCERT Solutions for Class 10 Maths Chapter 6 Triangles (Exercise)

Maths Chapter 6 Triangles class 10 Exercise: 6.1

Q1 (1) Fill in the blanks using the correct word given in brackets: All circles are ______ . (congruent, similar)

Answer:

All circles are similar.

Since all the circles have a similar shape. They may have different radii, but the shape of all circles is the same.

Therefore, all circles are similar.

Q1 (2) Fill in the blanks using the correct word given in brackets: All squares are ______. (similar, congruent)

Answer:

All squares are similar.

Since all the squares have a similar shape. They may have a different side, but the shape of all squares is the same.

Therefore, all squares are similar.

Q1 (3) Fill in the blanks using the correct word given in brackets: All ______triangles are similar. (isosceles, equilateral)

Answer:

All equilateral triangles are similar.

Since all the equilateral triangles have a similar shape. They may have different sides, but the shape of all equilateral triangles is the same.

Therefore, all equilateral triangles are similar.

Q1 (4) Fill in the blanks using the correct word given in brackets : (iv) Two polygons of the same number of sides are similar if(a) there corresponding angles are _________and (b) their corresponding sides are________. (equal, proportional)

Answer:

Two polygons of the same number of sides are similar if their corresponding angles are equal and their corresponding sides are proportional.

Thus, (a) equal

(b) proportional

Q2 (1) Give two different examples of a pair of similar figures.

Answer:

The two different examples of a pair of similar figures are :

1. Two circles with different radii.

2. Two rectangles with different breadth and length.

Q2 (2) Give two different examples of a pair of non-similar figures.

Answer:

The two different examples of a pair of non-similar figures are :

1. Rectangle and circle

2. A circle and a triangle.

Q3 State whether the following quadrilaterals are similar or not:

Answer:

Quadrilateral PQRS and ABCD are not similar as their corresponding sides are proportional, i.e. $1:2$, but their corresponding angles are not equal.

Class 10 Maths Chapter 6 Triangles Exercise: 6.2

Q1 In Fig. 6.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

Answer:

(i)

Let EC be x

Given: DE || BC

By using the proportionality theorem, we get

$\frac{AD}{DB}=\frac{AE}{EC}$

$\Rightarrow \frac{1.5}{3}=\frac{1}{x}$

$\Rightarrow x=\frac{3}{1.5}=2\, cm$

$\therefore EC=2\, cm$

(ii)

Let AD be x

Given: DE || BC

By using the proportionality theorem, we get

$\frac{AD}{DB}=\frac{AE}{EC}$

$\Rightarrow \frac{x}{7.2}=\frac{1.8}{5.4}$

$\Rightarrow x=\frac{7.2}{3}=2.4\, cm$

$\therefore AD=2.4\, cm$

Q2 (1) E and F are points on the sides PQ and PR respectively of a $\triangle$ PQR. For each of the following cases, state whether EF || QR: PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

Answer:

(i)

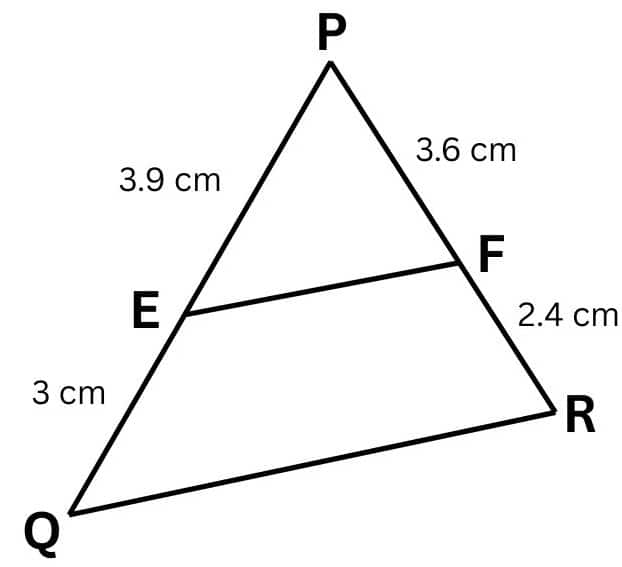
Given :

PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

$\frac{PE}{EQ}=\frac{3.9}{3}=1.3\, cm$ and $\frac{PF}{FR}=\frac{3.6}{2.4}=1.5\, cm$

We have

$\frac{PE}{EQ} \neq \frac{PF}{FR}$

Hence, EF is not parallel to QR.

Q2 (2) E and F are points on the sides PQ and PR, respectively, of a triangle PQR. For each of the following cases, state whether EF || QR : PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

Answer:

(ii)

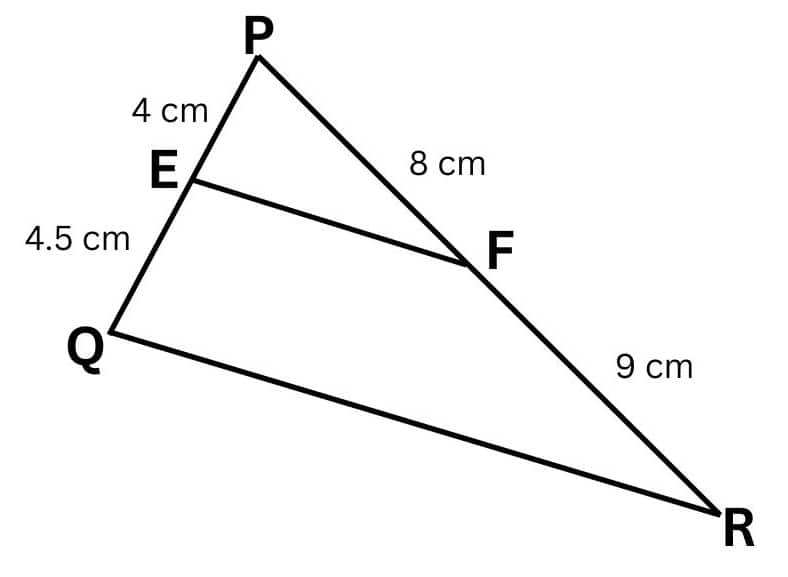
Given :

PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

$\frac{PE}{EQ}=\frac{4}{4.5}=\frac{8}{9}\, cm$ and $\frac{PF}{FR}=\frac{8}{9}\, cm$

We have

$\frac{PE}{EQ} = \frac{PF}{FR}$

Hence, EF is parallel to QR.

Q2 (3) E and F are points on the sides PQ and PR, respectively, of a triangle PQR. For each of the following cases, state whether EF || QR : PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

Answer:

(iii)

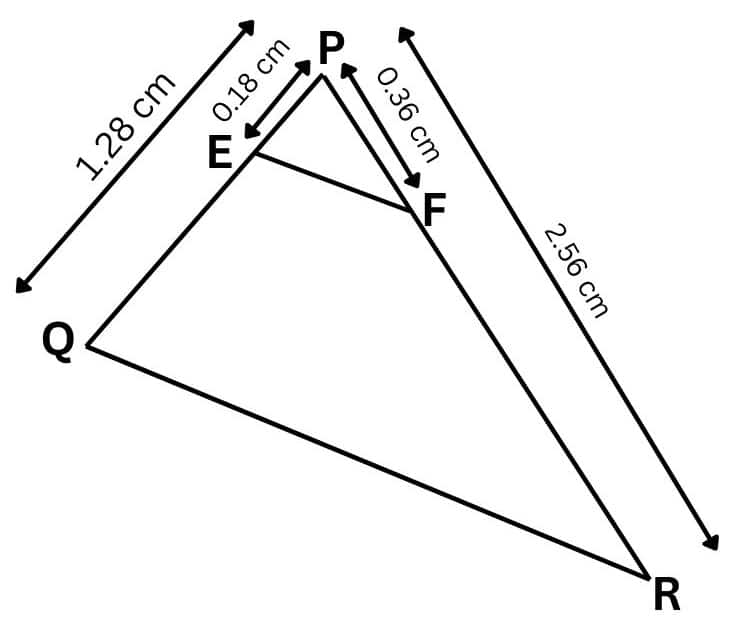
Given :

PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

$\frac{PE}{PQ}=\frac{0.18}{1.28}=\frac{9}{64}\, cm$ and $\frac{PF}{PR}=\frac{0.36}{2.56}=\frac{9}{64}\, cm$

We have

$\frac{PE}{EQ} = \frac{PF}{FR}$

Hence, EF is parallel to QR.

Q3 In Fig. 6.18, if LM || CB and LN || CD, prove that $\frac{AM}{AB} = \frac{AN}{AD }$

Answer:

Given : LM || CB and LN || CD

To prove :

$\frac{AM}{AB} = \frac{AN}{AD }$

Since , LM || CB so we have

$\frac{AM}{AB}=\frac{AL}{AC}.............................................1$

Also, LN || CD

$\frac{AL}{AC}=\frac{AN}{AD}.............................................2$

From equations 1 and 2, we have

$\frac{AM}{AB} = \frac{AN}{AD }$

Hence proved.

Q4 In Fig. 6.19, DE || AC and DF || AE. Prove that BF / FE = BE / EC

Answer:

Given: DE || AC and DF || AE.

To prove :

$\frac{BF}{FE} = \frac{BE}{EC }$

Since , DE || AC so we have

$\frac{BD}{DA}=\frac{BE}{EC}.............................................1$

Also, DF || AE

$\frac{BD}{DA}=\frac{BF}{FE}.............................................2$

From equations 1 and 2, we have

$\frac{BF}{FE} = \frac{BE}{EC }$

Hence proved.

Q5 In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.

Answer:

Given: DE || OQ and DF || OR.

To prove EF || QR.

Since DE || OQ so we have

$\frac{PE}{EQ}=\frac{PD}{DO}.............................................1$

Also, DF || OR

$\frac{PF}{FR}=\frac{PD}{DO}.............................................2$

From equations 1 and 2, we have

$\frac{PE}{EQ} = \frac{PF}{FR }$

Thus, EF || QR. (converse of basic proportionality theorem)

Hence proved.

Q6 In Fig. 6.21, A, B, and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Answer:

Given : AB || PQ and AC || PR

To prove: BC || QR

Since, AB || PQ so we have

$\frac{OA}{AP}=\frac{OB}{BQ}.............................................1$

Also, AC || PR

$\frac{OA}{AP}=\frac{OC}{CR}.............................................2$

From equations 1 and 2, we have

$\frac{OB}{BQ} = \frac{OC}{CR }$

Therefore, BC || QR. (converse basic proportionality theorem)

Hence proved.

Q7 Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX.)

Answer:

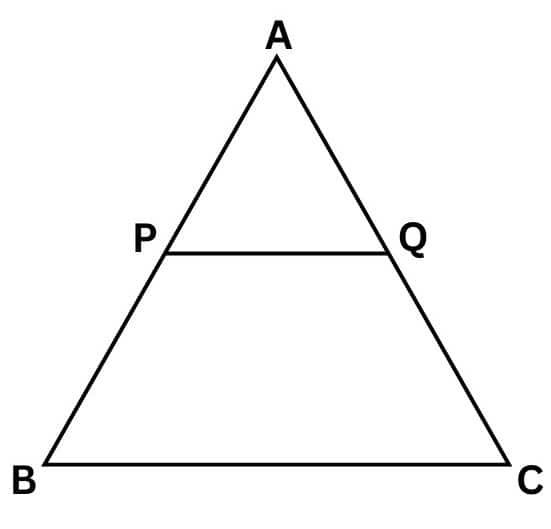
Let PQ be a line passing through the midpoint of line AB and parallel to line BC, intersecting line AC at point Q.

i.e. $PQ||BC$ and $AP=PB$ .

Using the basic proportionality theorem, we have

$\frac{AP}{PB}=\frac{AQ}{QC}..........................1$

Since $AP=PB$

$\frac{AQ}{QC}=\frac{1}{1}$

$\Rightarrow AQ=QC$

$\therefore$ Q is the midpoint of AC.

Q8 Using Theorem 6.2, prove that the line joining the midpoints of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX.)

Answer:

Let P be the midpoint of line AB and Q be the midpoint of line AC.

PQ is the line joining midpoints P and Q of lines AB and AC, respectively.

i.e. $AQ=QC$ and $AP=PB$ .

we have,

$\frac{AP}{PB}=\frac{1}{1}..........................1$

$\frac{AQ}{QC}=\frac{1}{1}...................................2$

From equations 1 and 2, we get

$\frac{AQ}{QC}=\frac{AP}{PB}$

$\therefore$ By basic proportionality theorem, we have $PQ||BC$

Q9 ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show
that $\frac{AO}{BO} = \frac{CO}{DO}$

Answer:

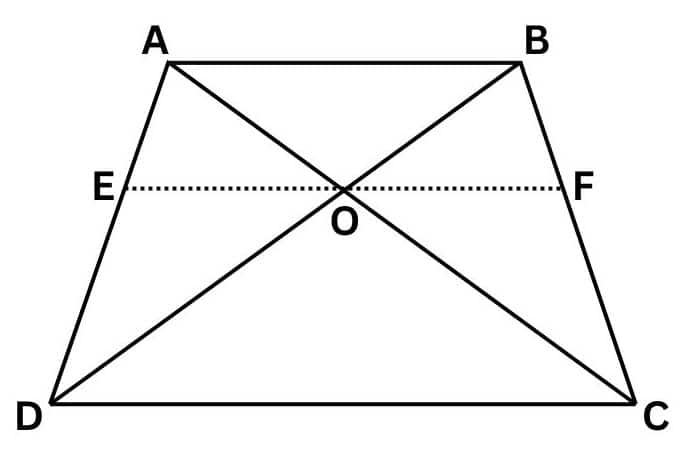
Draw a line EF passing through point O such that $EO||CD\, \, and\, \, FO||CD$

To prove :

$\frac{AO}{BO} = \frac{CO}{DO}$

In $\triangle ADC$ , we have $CD||EO$

So, by using the basic proportionality theorem,

$\frac{AE}{ED}=\frac{AO}{OC}........................................1$

In $\triangle ABD$ , we have $AB||EO$

So, by using the basic proportionality theorem,

$\frac{DE}{EA}=\frac{OD}{BO}........................................2$

Using equations 1 and 2, we get

$\frac{AO}{OC}=\frac{BO}{OD}$

$\Rightarrow \frac{AO}{BO} = \frac{CO}{DO}$

Hence proved.

Q10 The diagonals of a quadrilateral ABCD intersect each other at point O such that $\frac{AO}{BO} = \frac{CO}{DO}$. Show that ABCD is a trapezium.

Answer:

Draw a line EF passing through point O such that $EO||AB$

Given :

$\frac{AO}{BO} = \frac{CO}{DO}$

In $\triangle ABD$ , we have $AB||EO$

So, by using the basic proportionality theorem,

$\frac{AE}{ED}=\frac{BO}{DO}........................................1$

However, it is given that

$\frac{AO}{CO} = \frac{BO}{DO}..............................2$

Using equations 1 and 2, we get

$\frac{AE}{ED}=\frac{AO}{CO}$

$\Rightarrow EO||CD$ (By basic proportionality theorem)

$\Rightarrow AB||EO||CD$

$\Rightarrow AB||CD$

Therefore, ABCD is a trapezium.

Class 10 Maths Chapter 6 Triangles Exercise: 6.3

Q1 State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form :

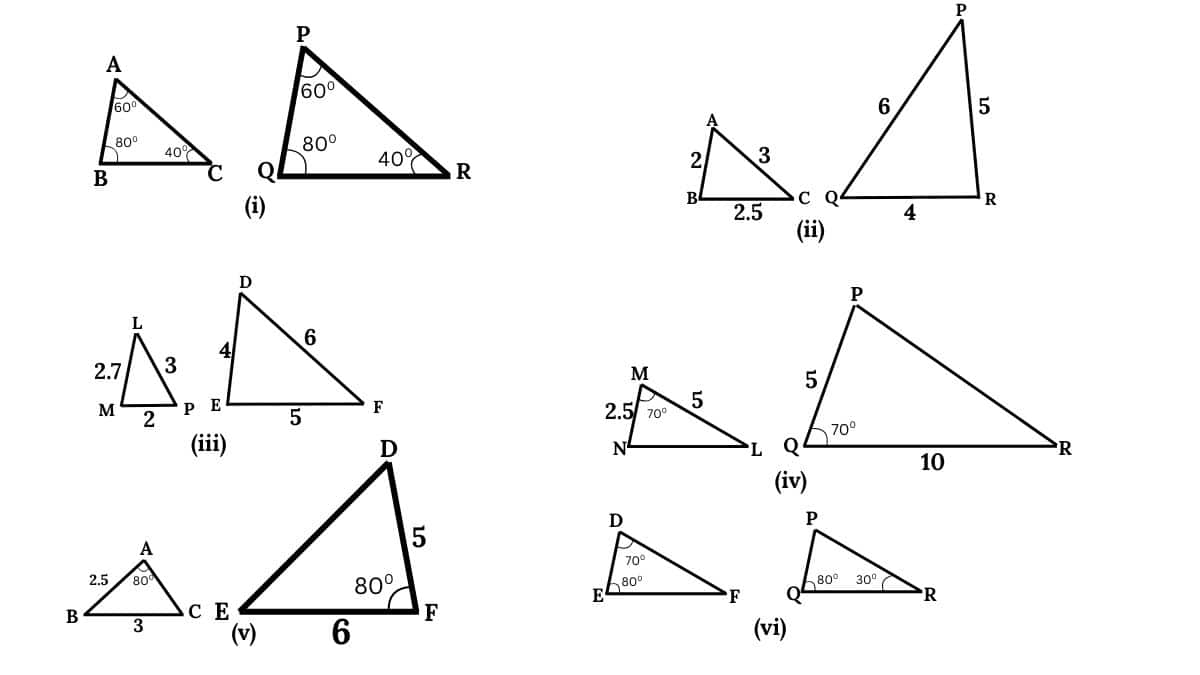
Answer:

(i) $\angle A=\angle P=60 ^\circ$

$\angle B=\angle Q=80 ^\circ$

$\angle C=\angle R=40 ^\circ$

$\therefore \triangle ABC \sim \triangle PQR$ (By AAA)

So , $\frac{AB}{QR}=\frac{BC}{RP}=\frac{CA}{PQ}$

(ii) As corresponding sides of both triangles are proportional.

$\therefore \triangle ABC \sim \triangle PQR$ (By SSS)

(iii) Given triangles are not similar because corresponding sides are not proportional.

(iv) $\triangle MNL \sim \triangle PQR$ by SAS similarity criteria.

(v) Given triangles are not similar because the corresponding angle is not contained by two corresponding sides

(vi) In $\triangle DEF$ , we know that

$\angle D+\angle E+\angle F=180 ^\circ$

$\Rightarrow 70 ^\circ+80 ^\circ+\angle F=180 ^\circ$

$\Rightarrow 150 ^\circ+\angle F=180 ^\circ$

$\Rightarrow \angle F=180 ^\circ-150 ^\circ=30 ^\circ$

In $\triangle PQR$ , we know that

$\angle P+\angle Q+\angle R=180 ^\circ$

$\Rightarrow 30^{\circ}+80^{\circ}+\angle R=180^{\circ}$

$\Rightarrow 110 ^\circ+\angle R=180 ^\circ$

$\Rightarrow \angle R=180 ^\circ-110 ^\circ=70 ^\circ$

$\angle Q=\angle P=70 ^\circ$

$\angle E=\angle Q=80^{\circ}$

$\angle F=\angle R=30 ^\circ$

$\therefore \triangle DEF\sim \triangle PQR$ ( By AAA)

Q2 In Fig. 6.35, $\Delta ODC \sim \Delta OBA$ , $\angle BOC = 125 ^\circ$ and $\angle CDO = 70 ^\circ$ . Find $\angle DOC , \angle DCO , \angle OAB$

Answer:

Given : $\Delta ODC \sim \Delta OBA$ , $\angle BOC = 125 ^\circ$ and $\angle CDO = 70 ^\circ$

$\angle DOC+\angle BOC=180 ^{\circ} $ (DOB is a straight line)

$\Rightarrow \angle DOC+125 ^\circ=180 ^\circ$

$\Rightarrow \angle DOC=180 ^\circ-125 ^\circ$

$\Rightarrow \angle DOC=55 ^\circ$

In $\Delta ODC, $

$\angle DOC+\angle ODC+\angle DCO=180 ^\circ$

$\Rightarrow 55 ^\circ+ 70 ^\circ+\angle DCO=180 ^\circ$

$\Rightarrow \angle DCO+125 ^\circ=180 ^\circ$

$\Rightarrow \angle DCO=180 ^\circ-125 ^\circ$

$\Rightarrow \angle DCO=55 ^\circ$

Since, $\Delta ODC \sim \Delta OBA$, so

$\Rightarrow\angle OAB= \angle DCO=55 ^{\circ} $ (Corresponding angles are equal in similar triangles).

Q3 Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\frac{OA }{OC} = \frac{OB }{OD }$

Answer:

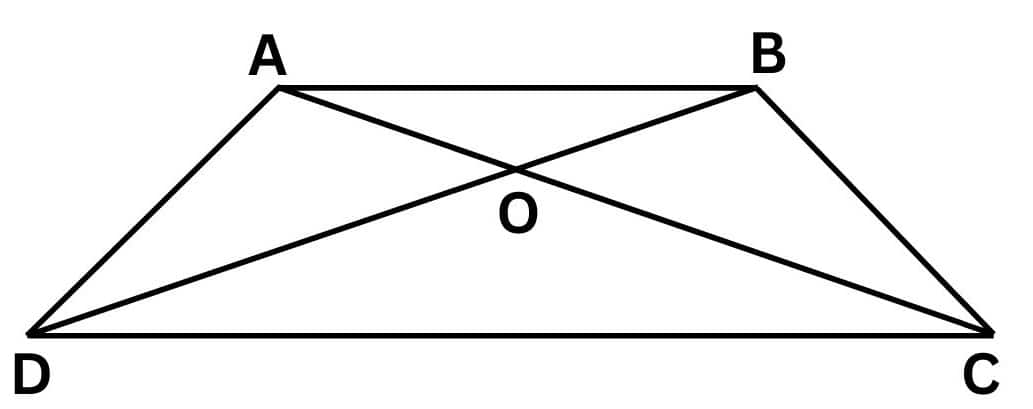
In $\triangle DOC\, and\, \triangle BOA$ , we have

$\angle CDO=\angle ABO$ ( Alternate interior angles as $AB||CD$ )

$\angle DCO=\angle BAO$ ( Alternate interior angles as $AB||CD$ )

$\angle DOC=\angle BOA$ ( Vertically opposite angles are equal)

$\therefore \triangle DOC\, \sim \, \triangle BOA$ ( By AAA)

$\therefore \frac{DO}{BO}=\frac{OC}{OA}$ ( corresponding sides are equal)

$\Rightarrow \frac{OA }{OC} = \frac{OB }{OD }$

Hence proved.

Q4 In Fig. 6.36, $\frac{QR }{QS } = \frac{QT}{PR}$ and $\angle 1 = \angle 2$ . Show that $\Delta PQS \sim \Delta TQR$

Answer:

Given : $\frac{QR }{QS } = \frac{QT}{PR}$ and $\angle 1 = \angle 2$

To prove : $\Delta PQS \sim \Delta TQR$

In $\triangle PQR$ , $\angle PQR=\angle PRQ$

$\therefore PQ=PR$

$\frac{QR }{QS } = \frac{QT}{PR}$ (Given)

$\Rightarrow \frac{QR }{QS } = \frac{QT}{PQ}$

In $\Delta PQS\, and\, \Delta TQR$,

$\Rightarrow \frac{QR }{QS } = \frac{QT}{PQ}$

$\angle Q=\angle Q$ (Common)

$\Delta PQS \sim \Delta TQR$ (By SAS)

Q5 S and T are points on sides PR and QR of $\Delta$ PQR such that $\angle$ P = $\angle$ RTS. Show that $\Delta$ RPQ ~ $\Delta$ RTS.

Answer:

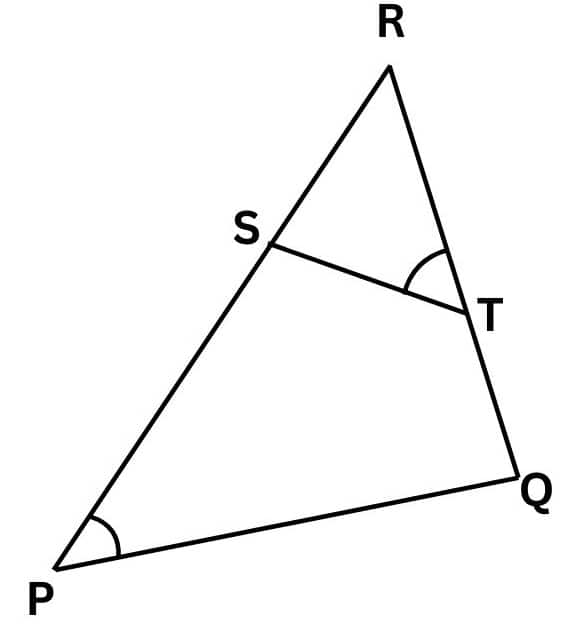
Given : $\angle$ P = $\angle$ RTS

To prove RPQ ~ $\Delta$ RTS.

In $\Delta$ RPQ and $\Delta$ RTS,

$\angle$ P = $\angle$ RTS (Given)

$\angle$ R = $\angle$ R (common)

$\Delta$ RPQ ~ $\Delta$ RTS. (By AA)

Q6 In Fig. 6.37, if $\Delta$ ABE $\equiv$ $\Delta$ ACD, show that $\Delta$ ADE ~ $\Delta$ ABC.

Answer:

Given: $\triangle ABE \cong \triangle ACD$

To prove ADE ~ $\Delta$ ABC.

Since $\triangle ABE \cong \triangle ACD$

$AB=AC$ (By CPCT)

$AD=AE$ (By CPCT)

In $\Delta$ ADE and $\Delta$ ABC,

$\angle A=\angle A$ (Common)

and

$\frac{AD}{AB}=\frac{AE}{AC}$ ( $AB=AC$ and $AD=AE$ )

Therefore, $\Delta$ ADE ~ $\Delta$ ABC. ( By SAS criteria)

Q7 (1) In Fig. 6.38, altitudes AD and CE of $\Delta ABC$ intersect each other at the point P. Show that: $\Delta AEP \sim \Delta CDP$

Answer:

To prove : $\Delta AEP \sim \Delta CDP$

In $\Delta AEP \, \, and\, \, \Delta CDP$ ,

$\angle AEP=\angle CDP$ ( Both angles are right angle)

$\angle APE=\angle CPD$ (Vertically opposite angles )

$\Delta AEP \sim \Delta CDP$ ( By AA criterion)

Q7 (2) In Fig. 6.38, altitudes AD and CE of $\Delta ABC$ intersect each other at the point P. Show that: $\Delta ABD \sim \Delta CBE$

Answer:

To prove : $\Delta ABD \sim \Delta CBE$

In $\Delta ABD \, \, and\, \, \Delta CBE$ ,

$\angle ADB=\angle CEB$ ( Both angles are right angle)

$\angle ABD=\angle CBE$ (Common )

$\Delta ABD \sim \Delta CBE$ ( By AA criterion)

Q7 (3) In Fig. 6.38, altitudes AD and CE of $\Delta ABC$ intersect each other at the point P. Show that: $\Delta AEP \sim \Delta ADB$

Answer:

To prove : $\Delta AEP \sim \Delta ADB$

In $\Delta AEP \, \, \, and\, \, \Delta ADB$ ,

$\angle AEP=\angle ADB$ ( Both angles are right angle)

$\angle A=\angle A$ (Common )

$\Delta AEP \sim \Delta ADB$ ( By AA criterion)

Q7 (4) In Fig. 6.38, altitudes AD and CE of $\Delta ABC$ intersect each other at the point P. Show that: $\Delta PDC \sim \Delta BEC$

Answer:

To prove : $\Delta PDC \sim \Delta BEC$

In $\Delta PDC \, \, and\, \, \, \Delta BEC$ ,

$\angle CDP=\angle CEB$ ( Both angles are right angle)

$\angle C=\angle C$ (Common )

$\Delta PDC \sim \Delta BEC$ ( By AA criterion)

Q8 E is a point on the side AD produced of a parallelogram ABCD, and BE intersects CD at F. Show that $\Delta ABE \sim \Delta CFB$.

Answer:

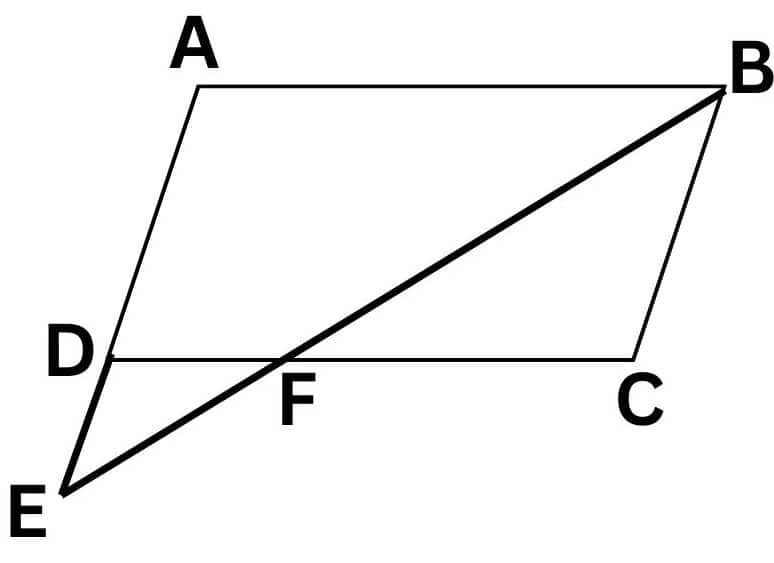
To prove : $\Delta ABE \sim \Delta CFB$

In $\Delta ABE \, \, \, and\, \, \Delta CFB$ ,

$\angle A=\angle C$ ( Opposite angles of a parallelogram are equal)

$\angle AEB=\angle CBF$ ( Alternate angles of AE||BC)

$\Delta ABE \sim \Delta CFB$ ( By AA criterion )

Q9 (1) In Fig. 6.39, ABC and AMP are two right triangles, right-angled at B and M, respectively. Prove that: $\Delta ABC \sim \Delta AMP$

Answer:

To prove : $\Delta ABC \sim \Delta AMP$

In $\Delta ABC \, \, and\, \, \Delta AMP$ ,

$\angle ABC=\angle AMP$ ( Each $90 ^\circ$ )

$\angle A=\angle A$ ( common)

$\Delta ABC \sim \Delta AMP$ ( By AA criterion )

Q9 In Fig. 6.39, ABC and AMP are two right triangles, right-angled at B and M, respectively. Prove that $\frac{CA }{PA } = \frac{BC }{MP}$

Answer:

To prove :

$\frac{CA }{PA } = \frac{BC }{MP}$

In $\Delta ABC \, \, and\, \, \Delta AMP$ ,

$\angle ABC=\angle AMP$ ( Each $90 ^\circ$ )

$\angle A=\angle A$ ( common)

$\Delta ABC \sim \Delta AMP$ ( By AA criterion )

$\frac{CA }{PA } = \frac{BC }{MP}$ ( corresponding parts of similar triangles )

Hence proved.

Q10 (1) CD and GH are respectively the bisectors of $\angle ACB$ and $\angle EGF$ such that D and H lie on sides AB and FE of $\Delta ABC\: \: and\: \: \Delta EGF$ respectively. If $\Delta ABC \sim \Delta EGF$ , show that: $\frac{CD}{GH} = \frac{AC}{FG}$

Answer:

To prove :

$\frac{CD}{GH} = \frac{AC}{FG}$

Given : $\Delta ABC \sim \Delta EGF$

$\angle A=\angle F,\angle B=\angle E\, \, and \, \, \angle ACB=\angle FGE,\angle ACB=\angle FGE$

$\therefore \angle ACD=\angle FGH$ ( CD and GH are bisectors of equal angles)

$\therefore \angle DCB=\angle HGE$ ( CD and GH are bisectors of equal angles)

In $\Delta ACD \, \, and\, \, \Delta FGH$

$\therefore \angle ACD=\angle FGH$ ( proved above)

$\angle A=\angle F$ ( proved above)

$\Delta ACD \sim \Delta FGH$ ( By AA criterion)

$\Rightarrow \frac{CD}{GH} = \frac{AC}{FG}$

Hence proved.

Q 10 (2) CD and GH are respectively the bisectors of $\angle ABC \: \: and \: \: \angle EGF$ such that D and H lie on sides AB and FE of $\Delta ABC \: \: and \: \: \Delta EGF$ respectively. If $\Delta ABC \sim \Delta EGF$ , show that: $\Delta DCB \sim \Delta HGE$

Answer:

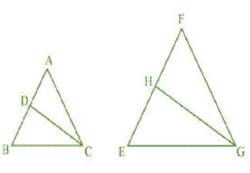
To prove : $\Delta DCB \sim \Delta HGE$

Given : $\Delta ABC \sim \Delta EGF$

In $\Delta DCB \,\, \, and\, \, \Delta HGE$ ,

$\therefore \angle DCB=\angle HGE$ ( CD and GH are bisectors of equal angles)

$\angle B=\angle E$ ( $\Delta ABC \sim \Delta EGF$ )

$\Delta DCB \sim \Delta HGE$ ( By AA criterion )

Q10 (3) CD and GH are respectively the bisectors of $\angle ABC \: \: and \: \: \angle EGF$ such that D and H lie on sides AB and FE of $\Delta ABC \: \: and \: \: \Delta EGF$ respectively. If $\Delta ABC\sim \Delta EGF$ , show that: $\Delta DCA \sim \Delta HGF$

Answer:

To prove : $\Delta DCA \sim \Delta HGF$

Given : $\Delta ABC \sim \Delta EGF$

In $\Delta DCA \, \, \, and\, \, \Delta HGF$ ,

$\therefore \angle ACD=\angle FGH$ ( CD and GH are bisectors of equal angles)

$\angle A=\angle F$ ( $\Delta ABC \sim \Delta EGF$ )

$\Delta DCA \sim \Delta HGF$ ( By AA criterion )

Q11 In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If $AD \perp BC$ and $EF \perp AC$ , prove that $\Delta ABD \sim \Delta ECF$

Answer:

To prove : $\Delta ABD \sim \Delta ECF$

Given: ABC is an isosceles triangle.

$AB=AC \, \, and\, \, \angle B=\angle C$

In $\Delta ABD \, \, and\, \, \Delta ECF$ ,

$\angle ABD=\angle ECF$ ( $\angle ABD=\angle B=\angle C=\angle ECF$ )

$\angle ADB=\angle EFC$ ( Each $90 ^\circ$ )

$\Delta ABD \sim \Delta ECF$ ( By AA criterion)

Q12 Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of $\Delta PQR$ (see Fig. 6.41). Show that $\Delta ABC \sim \Delta PQR$

Answer:

AD and PM are medians of triangles. So,

$BD=\frac{BC}{2}\, and\, QM=\frac{QR}{2}$

Given :

$\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AD}{PM}$

$\Rightarrow \frac{AB}{PQ}=\frac{\frac{1}{2}BC}{\frac{1}{2}QR}=\frac{AD}{PM}$

$\Rightarrow \frac{AB}{PQ}=\frac{BD}{QM}=\frac{AD}{PM}$

In $\triangle ABD\, and\, \triangle PQM,$

$\frac{AB}{PQ}=\frac{BD}{QM}=\frac{AD}{PM}$

$\therefore \triangle ABD\sim \triangle PQM,$ (SSS similarity)

$\Rightarrow \angle ABD=\angle PQM$ ( Corresponding angles of similar triangles )

In $\triangle ABC\, and\, \triangle PQR,$

$\Rightarrow \angle ABD=\angle PQM$ (proved above)

$\frac{AB}{PQ}=\frac{BC}{QR}$

Therefore, $\Delta ABC \sim \Delta PQR$ . ( SAS similarity)

Q13 D is a point on the side BC of a triangle ABC such that $\angle ADC = \angle BAC$. Show that $CA^2 = CB.CD.$

Answer:

In, $\triangle ADC \, \, and\, \, \triangle BAC,$

$\angle ADC = \angle BAC$ ( given )

$\angle ACD = \angle BCA$ (common )

$\triangle ADC \, \, \sim \, \, \triangle BAC,$ ( By AA rule)

$\frac{CA}{CB}=\frac{CD}{CA}$ ( corresponding sides of similar triangles )

$\Rightarrow CA^2=CB\times CD$

Q14 Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that $\Delta ABC \sim \Delta PQR$

Answer:

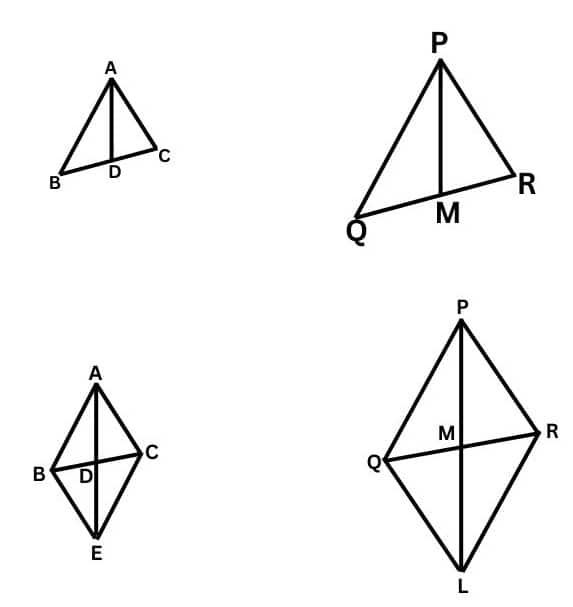
$\frac{AB}{PQ}=\frac{AC}{PR}=\frac{AD}{PM}$ (given)

Produce AD and PM to E and L such that AD=DE and PM=DE. Now,

join B to E, C to E, Q to L and R to L.

AD and PM are medians of a triangle; therefore

QM=MR and BD=DC

AD = DE (By construction)

PM=ML (By construction)

So, diagonals of ABEC bisecting each other at D, so ABEC is a parallelogram.

Similarly, PQLR is also a parallelogram.

Therefore, AC=BE ,AB=EC and PR=QL,PQ=LR

$\frac{AB}{PQ}=\frac{AC}{PR}=\frac{AD}{PM}$ (Given )

$\Rightarrow \frac{AB}{PQ}=\frac{BE}{QL}=\frac{2.AD}{2.PM}$

$\Rightarrow \frac{AB}{PQ}=\frac{BE}{QL}=\frac{AE}{PL}$

$\Delta ABE \sim \Delta PQL$ (SSS similarity)

$\angle BAE=\angle QPL$ ...................1 (Corresponding angles of similar triangles)

Similarity, $\triangle AEC=\triangle PLR$

$\angle CAE=\angle RPL$ ........................2

Adding equations 1 and 2,

$\angle BAE+\angle CAE=\angle QPL+\angle RPL$

$\angle CAB=\angle RPQ$ ............................3

In $\triangle ABC\, and\, \, \triangle PQR,$

$\frac{AB}{PQ}=\frac{AC}{PR}$ ( Given )

$\angle CAB=\angle RPQ$ ( From above equation 3)

$\triangle ABC\sim \triangle PQR$ ( SAS similarity)

Q15 A vertical pole of length 6 m casts a shadow 4 m long on the ground, and at the same time, a tower casts a shadow 28 m long. Find the height of the tower.

Answer:

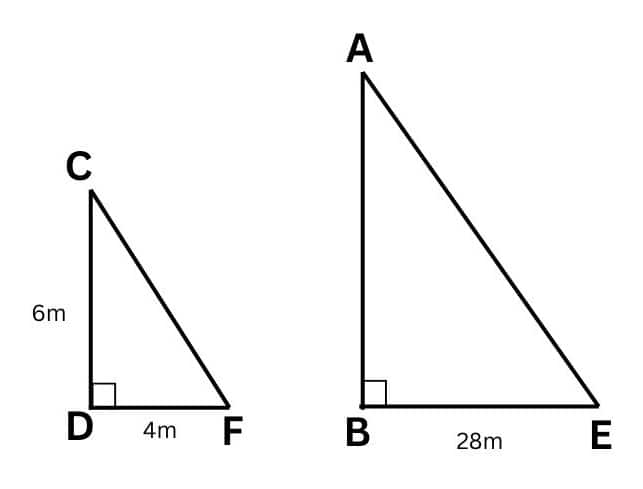
CD = pole

AB = tower

Shadow of pole = DF

Shadow of tower = BE

In $\triangle ABE\, \, and\, \triangle CDF,$

$\angle CDF=\angle ABE$ ( Each $90 ^\circ$ )

$\angle DCF=\angle BAE$ (Angle of sun at same place )

$\triangle ABE\, \, \sim \, \triangle CDF,$ (AA similarity)

$\frac{AB}{CD}=\frac{BE}{QL}$

$\Rightarrow \frac{AB}{6}=\frac{28}{4}$

$\Rightarrow AB=42$ cm

Hence, the height of the tower is 42 cm.

Q16 If AD and PM are medians of triangles ABC and PQR, respectively, where $\Delta AB C \sim \Delta PQR$, prove that $\frac{AB}{PQ} = \frac{AD }{PM}$

Answer:

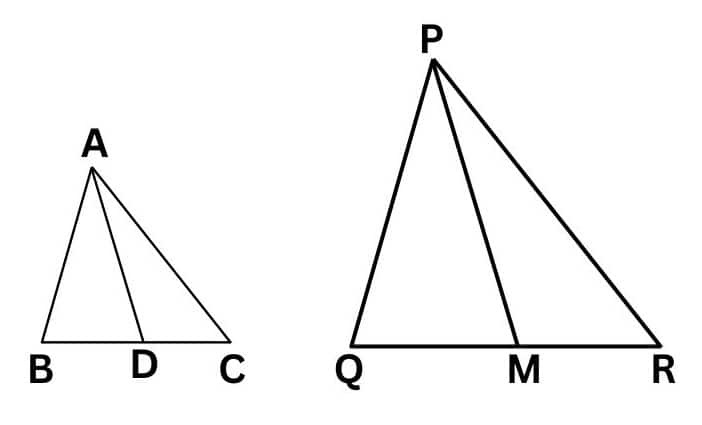
$\Delta AB C \sim \Delta PQR$ ( Given )

$\frac{AB}{PQ}=\frac{AC}{PR}=\frac{BC}{QR}$ ............... ....1( corresponding sides of similar triangles )

$\angle A=\angle P,\angle B=\angle Q,\angle C=\angle R$ ....................................2

AD and PM are medians of a triangle. So,

$BD=\frac{BC}{2}\, and\, QM=\frac{QR}{2}$ ..........................................3

From equations 1 and 3, we have

$\frac{AB}{PQ}=\frac{BD}{QM}$ ...................................................................4

In $\triangle ABD\, and\, \triangle PQM,$

$\angle B=\angle Q$ (From equation 2)

$\frac{AB}{PQ}=\frac{BD}{QM}$ (From equation 4)

$\triangle ABD\, \sim \, \triangle PQM, $ (SAS similarity)

$\frac{AB}{PQ}=\frac{BD}{QM}=\frac{AD}{PM}$

Importance of solving 10th Class Maths Triangles NCERT Questions

• Class 10 Maths Chapter 6 NCERT solutions are solved by subject-matter experts and are very reliable at the same time. The solutions provide shortcuts as well as detailed explanations with the necessary formulae that will help students understand the answers better.
• These solutions will help students manage their time efficiently in this chapter and understand which questions are easier to approach and which are time-consuming. This will be helpful during the exam.
• NCERT solutions for class 10 maths chapter 6 Triangle is designed to give the students step-by-step solutions for a particular question.

Triangles Class 10 Solutions - Exercise Wise

Here are the exercise-wise links for NCERT class 10, Chapter 6 Polynomial:

• Triangles Class 10 Ex 6.1
• Triangles Class 10 Ex 6.2
• Triangles Class 10 Ex 6.3

NCERT Solutions Of Class 10 - Subject Wise

For subject-wise solutions, Students can refer to the following links.

• NCERT solutions for class 10 maths
• NCERT solutions for class 10 science

NCERT Books and NCERT Syllabus

To refer to the syllabus and books, students can click on the following links.

• NCERT Books Class 10 Maths
• NCERT Syllabus Class 10 Maths
• NCERT Books Class 10
• NCERT Syllabus Class 10

NCERT Exemplar Solutions - Subject Wise

Given below are the subject-wise exemplar solutions of class 10 NCERT:

• NCERT Exemplar Class 10th Maths
• NCERT Exemplar Class 10th Science