Introduction to Trigonometry Class 10th Notes - Free NCERT Class 10 Maths Chapter 8 Notes - Download PDF

Introduction to Trigonometry Class 10 Notes: Free PDF Download

Use the link below to download the Introduction to Trigonometry Class 10 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 10 Maths Chapter 8 Notes: Introduction to Trigonometry

The study of trigonometry is all about how angles, together with triangle side lengths, relate within right triangles. Multiple practical applications rely heavily on trigonometry for their operation, including physics together with engineering and navigation. Mainly, it deals with right-angled triangles, where one angle is always 90°.

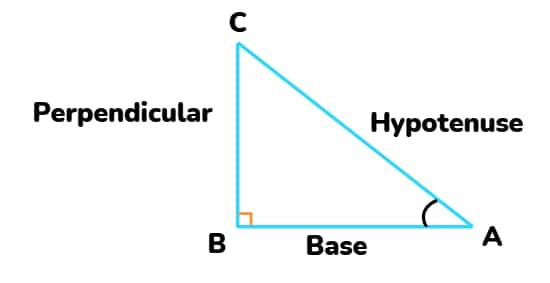
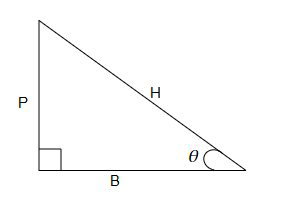
Components of Right-Angled Triangle:

In a right-angled triangle, there are three sides, which are as follows:

• Hypotenuse: The longest side opposite the right angle.
• Base: The horizontal side.
• Perpendicular: The vertical side.

These sides help define trigonometric ratios, which relate angles to sides.

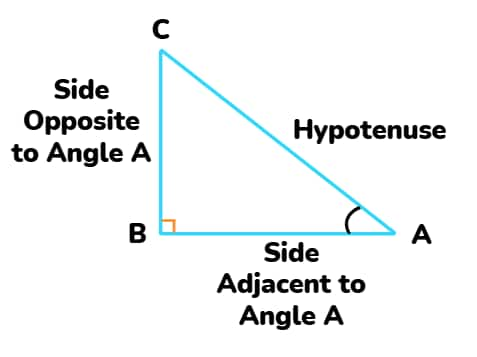
Opposite and Adjacent Sides in a right-angled triangle:

Here, in the diagram below, ∠CAB (or ∠A) is an acute angle. Note the position of the side BC to ∠A. It faces ∠A. We call it the side opposite angle A. Side AC is the hypotenuse of the right triangle shown below, and the side AB is a part of ∠A. So, call it the side adjacent to angle A.

Trigonometry Ratios:

The ratios of right-angled triangle sides relative to its acute angles form the basis of Trigonometric Ratios. The ratios serve to express how angle measurements relate to the lengths of triangle segments.

Six Trigonometric Ratios:

The six fundamental trigonometric ratios are:

• Sine (sin θ) = Perpendicular / Hypotenuse
  Sin⁡θ = $\frac{p}{h}$
• Cosine (cos θ) = Base / Hypotenuse
  Cosθ = $\frac{b}{h}$
• Tangent (tan θ) = Perpendicular / Base
  Tanθ = $\frac{p}{b}$
• Cosecant (cosec θ) = Hypotenuse / Perpendicular (Reciprocal of sine)
  Cosecθ = $\frac{h}{p}$
• Secant (sec θ) = Hypotenuse / Base (Reciprocal of cosine)
  Secθ = $\frac{h}{b}$
• Cotangent (cot θ) = Base / Perpendicular (Reciprocal of tangent)
  Cotθ = $\frac{b}{p}$

• Many practical problems in distances, heights and navigation, along with physics, require solutions by using ratios. The ratios serve as principles to understand both trigonometric identities and functions.

Many practical problems in distances, heights and navigation, along with physics, require solutions by using ratios. The ratios serve as principles to understand both trigonometric identities and functions.

Trigonometric Ratios of Some Specific Angles:

In trigonometry, certain angles commonly appear in problems, such as 0°, 30°, 45°, 60°, and 90°. Trigonometric ratios of standard angles maintain constant values, which enable smooth solutions to mathematical and practical applications.

1. Trigonometric Ratios of 45°

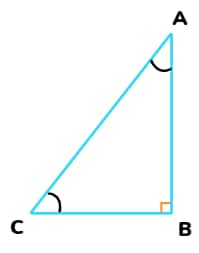
In triangle ABC, right-angled at B, if one angle is 45°, then the other angle is also 45°, i.e., ∠A = ∠C = 45°.

So, BC = AB (sides opposite to equal angles are equal)

Now, Suppose BC = AB = $a$.

Then by Pythagoras' Theorem, AC² = AB² + BC²
$ a^2 + a^2 = 2a^2 $

Hence, AC = √2 $a$

Using the definitions of the trigonometric ratios:

Sin 45° = $\frac{Perpendicular}{Hypotenuse} = \frac{AB}{AC} = \frac{a}{√2 a} = \frac{1}{√2} $

Cos 45° = $\frac{Base}{Hypotenuse} = \frac{BC}{AC} = \frac{a}{√2 a} = \frac{1}{√2} $

Tan 45° = $\frac{Perpendicular}{Base} = \frac{AB}{BC} = \frac{a}{a} $ = 1

Cosec 45° = $ \frac{1}{Sin 45°} = √2 $

Sec 45° = $ \frac{1}{Cos 45°} = √2 $

Cot 45° = $ \frac{1}{Tan 45°} $= 1

2. Trigonometric Ratios of 30° and 60°

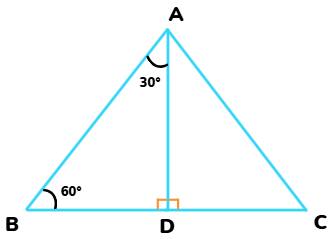
Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, ∠A = ∠B = ∠C = 60°.

Draw the perpendicular AD from A to the side BC.

From the Triangles Theorem, ABD ≌ ACD

And, BD = DC, ∠BAD = ∠CAD = 30°

Now, let's suppose that AB = 2$a$.

BD = $\frac{1}{2}BC = a $

And, AD² = AB² – BD² = (2$a$)² – ($a$)² = 3$a$²

So, AD = √3 $a$

Using the definitions of the trigonometric ratios:

Sin 30° = $\frac{Perpendicular}{Hypotenuse} = \frac{BD}{AB} = \frac{a}{2a} = \frac{1}{2} $

Cos 30° = $\frac{Base}{Hypotenuse} = \frac{AD}{AB} = \frac{√3 a}{2 a} = \frac{√3}{2} $

Tan 30° = $\frac{Perpendicular}{Base} = \frac{BD}{AD} = \frac{a}{√3 a} = \frac{1}{√3} $

Cosec 30° = $ \frac{1}{Sin 30°}$ = 2

Sec 30° = $ \frac{1}{Cos 30°} = \frac{2}{√3} $

Cot 30° = $ \frac{1}{Tan 30°}$ = √3

Same for 60°

Sin 60° = $\frac{√3}{2} $

Cos 60° = $\frac{1}{2} $

Tan 60° = √3

Cosec 60° = $ \frac{1}{Sin 60°}$ = $ \frac{2}{√3} $

Sec 60° = $ \frac{1}{Cos 60°}$ = 2

Cot 60° =$ \frac{1}{Tan 60°}$ =$\frac{1}{√3} $

3. Trigonometric Ratios of 0° and 90°

When the angle is 0°, the perpendicular side becomes 0, and the hypotenuse is equal to the base.

So, in this case,

Sin 0° = $\frac{Perpendicular}{Hypotenuse}$ = 0

Cos 0° = $\frac{Base}{Hypotenuse} $ = 1

Tan 0° = $\frac{Perpendicular}{Base}$ = 0

Cosec 0° = $ \frac{1}{Sin 0°}$ = Not defined

Sec 0° =$ \frac{1}{Cos 0°}$ = 1

Cot 0° =$ \frac{1}{Tan 0°}$ = Not defined

When the angle is 90°, the base becomes 0, and the hypotenuse is equal to the perpendicular.

So, in this case,

Sin 90° = $\frac{Perpendicular}{Hypotenuse}$ = 1

Cos 90° = $\frac{Base}{Hypotenuse} $ = 0

Tan 90° = $\frac{Perpendicular}{Base}$ = Not defined

Cosec 90° = $ \frac{1}{Sin 90°}$ = 1

Sec 90° =$ \frac{1}{Cos 90°}$ = Not defined

Cot 90° =$ \frac{1}{Tan 90°}$ = 0

Trigonometric Identities:

Trigonometric identities are fundamental equations that hold for all values of an angle. The three most important identities are:

1. cos² A + sin² A = 1
2. 1 + tan² A = sec² A
3. cot² A + 1 = cosec² A

Proof:

1. cos² A + sin² A = 1

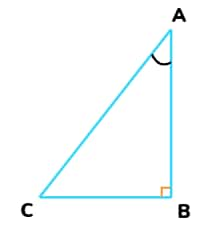
In ABC, right-angled at B,

AB² + BC² = AC²

Dividing each term by AC²,

$ \frac{AB^2}{AC^2} + \frac{BC^2}{AC^2} = \frac{AC^2}{AC^2} $

I.e. $ (\frac{AB}{AC})^2 + (\frac{BC}{AC})^2 = (\frac{AC}{AC})^2 $

And, from trigonometry ratios, this becomes:

(cos A)² + (sin A)² =1

cos² A + sin² A = 1

2. 1 + tan² A = sec² A

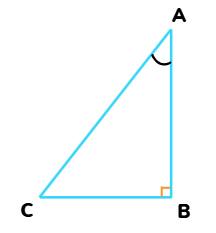
In ABC, right-angled at B,

AB² + BC² = AC²

Dividing each term by AB²,

$ \frac{AB^2}{AB^2} + \frac{BC^2}{AB^2} = \frac{AC^2}{AB^2} $

I.e. $ (\frac{AB}{AB})^2 + (\frac{BC}{AB})^2 = (\frac{AC}{AB})^2 $

And, from trigonometry ratios, this becomes:

1 + (tan A)² = (sec A)²

1 + tan² A = sec² A

3. cot² A + 1 = cosec² A

In ABC, right-angled at B,

AB² + BC² = AC²

Dividing each term by BC²,

$ \frac{AB^2}{BC^2} + \frac{BC^2}{BC^2} = \frac{AC^2}{BC^2} $

I.e. $ (\frac{AB}{BC})^2 + (\frac{BC}{BC})^2 = (\frac{AC}{BC})^2 $

And, from trigonometry ratios, this becomes:

(cot A)² + 1 = (cosec A)²

cot² A + 1 = cosec² A

Introduction to Trigonometry: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 10 chapter 8, Introduction to Trigonometry:

Question 1: Prove that $\frac{\sin \theta}{1+\cos \theta}+\frac{1+\cos \theta}{\sin \theta}=2 \operatorname{cosec} \theta$.

Solution:
LHS = $\frac{\sin \theta}{1+\cos \theta}+\frac{1+\cos \theta}{\sin \theta}$

$= \frac{\sin^2 \theta + (1+\cos \theta)^2}{\sin \theta (1+\cos \theta)}$

$= \frac{\sin^2 \theta + 1 + 2\cos \theta + \cos^2 \theta}{\sin \theta (1+\cos \theta)}$

$=\frac{(\sin^2 \theta + \cos^2 \theta) + 1 + 2\cos \theta}{\sin \theta (1+\cos \theta)}$

$=\frac{1 + 1 + 2\cos \theta}{\sin \theta (1+\cos \theta)}$

$=\frac{2 + 2\cos \theta}{\sin \theta (1+\cos \theta)}$

$=\frac{2(1+\cos \theta)}{\sin \theta (1+\cos \theta)}$

$=\frac{2}{\sin \theta}$

$=2 \operatorname{cosec} \theta$ = RHS

Hence, the given statement is proved.

Question 2: If $\sin \theta=\frac{1}{9}$, then $\tan \theta$ is equal to:

Solution:
$\sin \theta = \frac{1}{9}$.
$\sin \theta = \frac{P}{H}$
Let $P=k, H=9k$
Using Pythagoras' theorem,

$P^2+B^2=H^2$
$\Rightarrow k^2+B^2=9k^2$
$\Rightarrow B^2=80k^2$
$\Rightarrow B=4\sqrt{5}k$
$\tan\theta=\frac{P}{B}$
$\Rightarrow \tan\theta=\frac{k}{4\sqrt{5}k}=\frac{1}{4\sqrt{5}}$
Hence, the correct answer is $\frac{1}{4\sqrt{5}}$.

Question 3: Evaluate: $\frac{\cos 45^{\circ}}{\tan 30^{\circ}+\sin 60^{\circ}}$

Solution:
Given: $\frac{\cos 45^{\circ}}{\tan 30^{\circ}+\sin 60^{\circ}} = \frac{\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{3}} + \frac{\sqrt{3}}{2}} $

$= \frac{\frac{1}{\sqrt{2}}}{\frac{2+3}{2\sqrt{3}}} $

$= \frac{\frac{1}{\sqrt{2}}}{\frac{5}{2\sqrt{3}}} $

$= \frac{1}{\sqrt{2}} \times \frac{2\sqrt{3}}{5} $

$= \frac{2\sqrt{3}}{5\sqrt{2}} $

$= \frac{2\sqrt{6}}{10}$

$= \frac{\sqrt{6}}{5}$

Hence, the answer is $ \frac{\sqrt{6}}{5}$.

Class 10 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Exemplar Solutions for Class 10

• NCERT Exemplar Class 10 Maths solutions

• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths

• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10

• NCERT Syllabus for Class 10