Real Numbers Class 10th Notes - Free NCERT Class 10 Maths Chapter 1 Notes - Download PDF

Real Numbers Class 10 Notes PDF download: Free PDF Download

Students who wish to access the Real Numbers Class 10 Maths notes can click on the link below to download the entire notes in PDF.

Download PDF

Real Numbers Class 10 Notes

Careers360 has prepared these Class 10 Real Numbers Notes to make your revision smoother and faster.

Real numbers: These numbers are defined as those that can be represented on the number line. They are further divided into two parts such as rational and irrational numbers. They can be represented as R. The real numbers chart is given below for a better understanding.

Types of Numbers

There are mainly two types of numbers, such as real numbers and Imaginary numbers. For a better understanding, look at the chart given below.

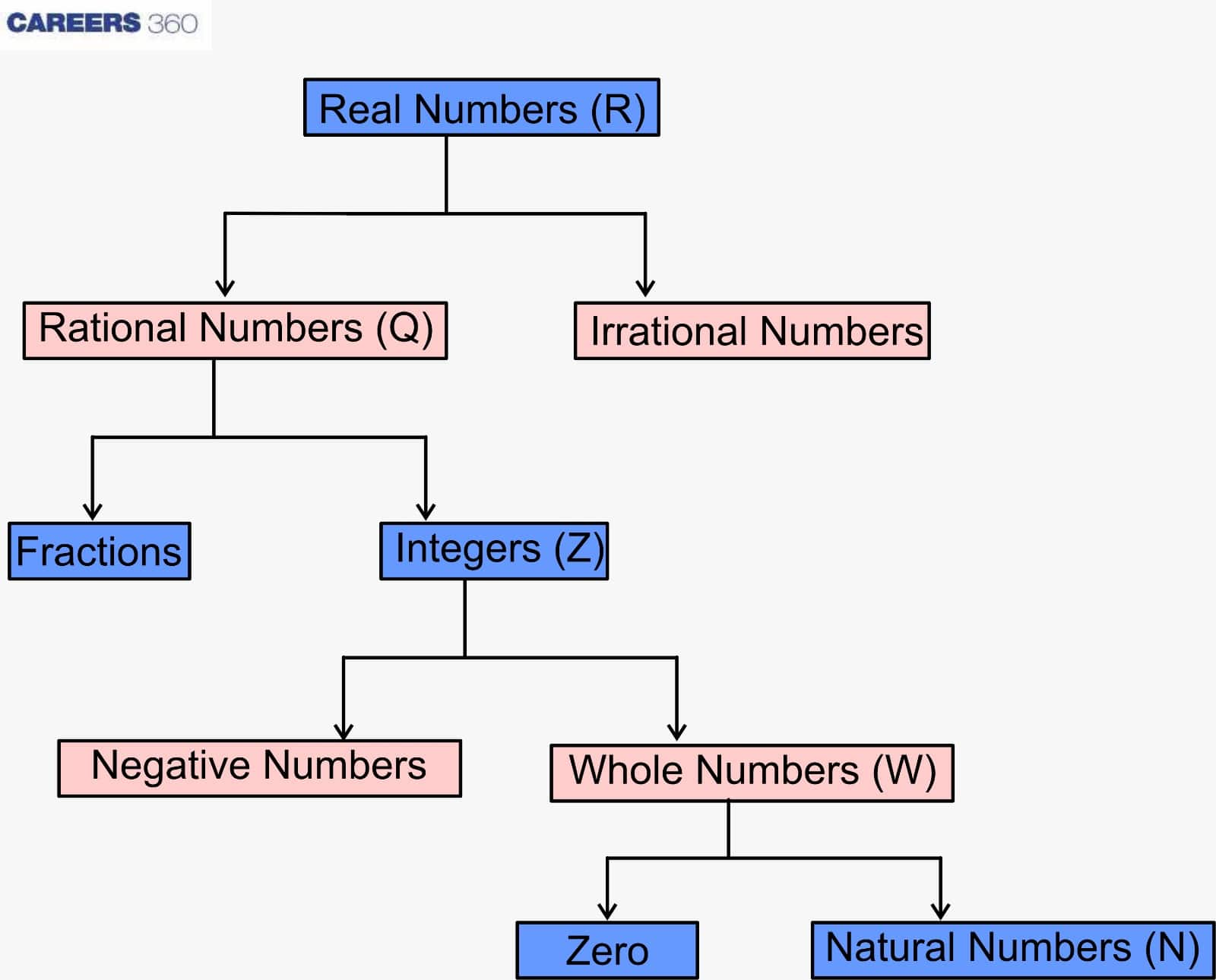
1. Natural Numbers: These are the numbers that start from the count of one till infinity. The natural numbers can be represented by “N”.
Example: N = {1, 2, 3, 4, 5, 6……}

2. Whole Numbers: These include all natural numbers but start from the count of zero. The whole numbers can be represented by “W”.
Example: W = { 0, 1, 2, 3, 4, 5, 6…...}

3. Integers: These are the numbers that include both positive and negative numbers along with zero.
Example: {…-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5……}

4. Rational numbers: These are the numbers that are any real
number and can be expressed in the form pq of R where the denominator q≠0. It is represented by "Q". It is noted that every integer number is a rational number.
Example: 12, 34, −78, 0.3333..., etc.

5. Irrational numbers: These are the numbers that cannot be expressed in the form pq of R where the denominator q≠0.
Example: √2,√3, π, 0.34343..., etc.

6. Prime numbers: The prime numbers are those numbers that can not be divided by any number other than 1 and the number itself.
Example: 2,3, 5, 7, 11, etc.

7. Composite numbers: The composite numbers are those numbers that can be divided by at least one of the numbers other than 1 and itself.
Example: 4, 6, 8, 9, 12, etc.

8. Co-primes: The co-primes are those numbers whose HCF is 1.
Example: (13, 21) (19, 23) etc.

Euclid’s Division Lemma

According to Euclid’s division Lemma, for two positive integers, a and b, there exists a unique integer such that a = bq + r, where 0≤r<b. Where a is a dividend, b is a divisor, q is a quotient, and r is the remainder. The lemma is always equivalent to: Dividend = Divisor × Quotient + Remainder.

Usage of Euclid's Division Lemma

Euclid’s Division Lemma can be used in finding the highest common factor of any two positive integers.

The steps are included to find HCF with the help of Euclid’s Division Lemma.

• Let the two positive integers be a and b, where “a” is greater than “b”.

Now, applying Euclid’s division to these numbers a and b, also find the two numbers q and r.

• In this step, check the value of r; if it is found to be 0, then b is the HCF of these numbers.

• Continuing this process until we get the value 0. Reaching the value of 0 makes the divisor b the HCF of a and b.

The Fundamental Theorem of Arithmetic

The fundamental theorem of arithmetic states that composite numbers can be expressed as the product of prime numbers.

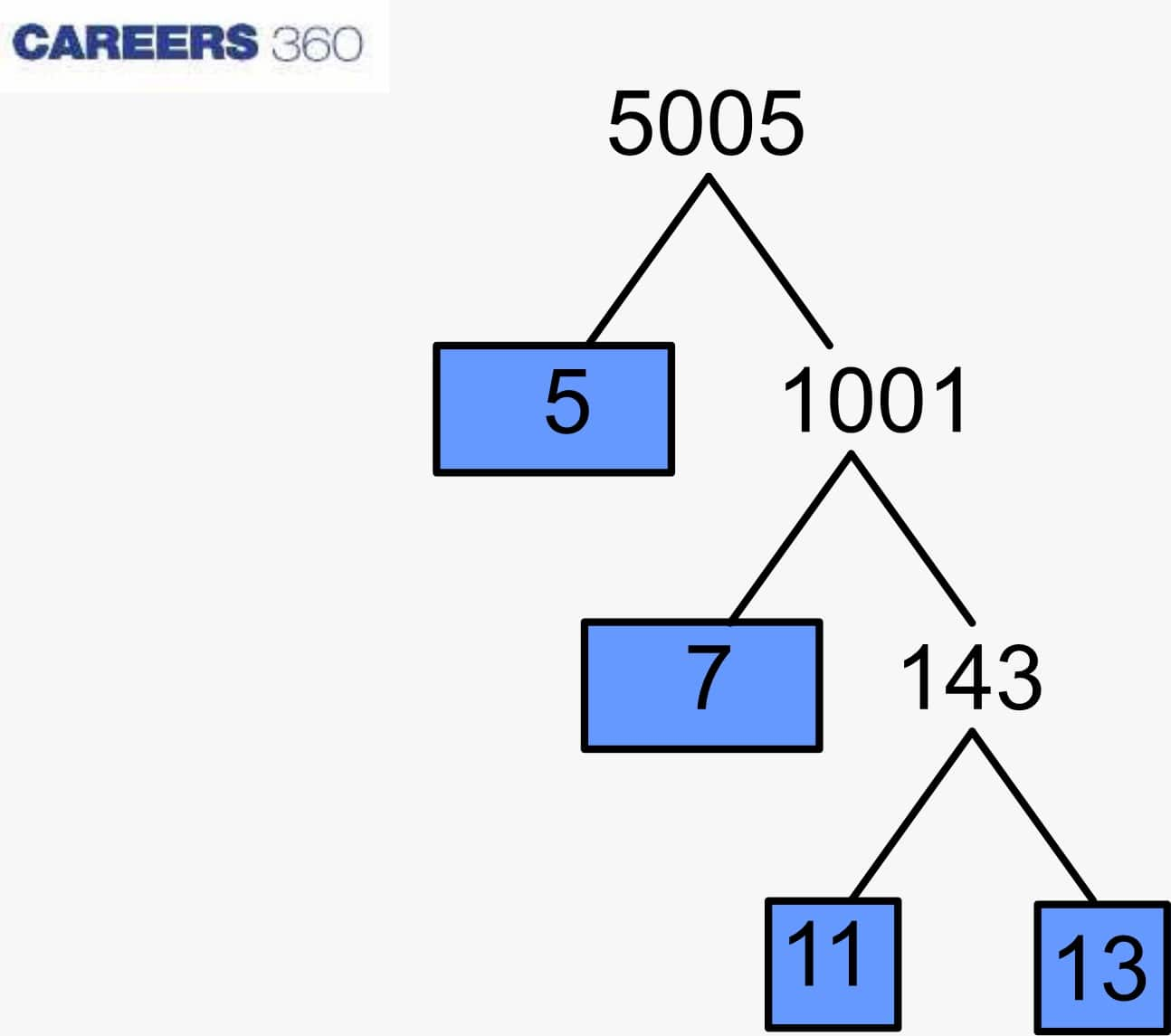
In the above-given arrangement, the highlighted numbers are the prime numbers. Thus, the prime factors are: 5, 7, 11 and 13.

Statement: Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factor occurs.
For example:
33=3×11
21=3×7
6=2×3

HCF And LCM by Prime Factorisation

HCF: HCF is the highest common factor, also known as the greatest common divisor (GCD). It is defined as the greatest number that divides each of the given numbers without leaving any remainder, as the highest common factor (HCF) of two or more given numbers.
The HCF can be calculated using two methods such as:

1) Prime factorisation: In this method, we express the given numbers as the products of their respective prime factors. After that, we select the common prime factors from the product of both numbers
Example: – To find the H.C.F of 28 and 35
Prime factors of 28 = 2 × 2 × 7
Prime factors of 35 = 7 × 5
The factor common to 28 and 35 is 7, which in turn is the HCF of 28 and 35.

(2) Euclid’s division algorithm: It is defined as the multiple use of Euclid’s division lemma to find the HCF of two numbers.

Example: To find the HCF of 16 and 58.

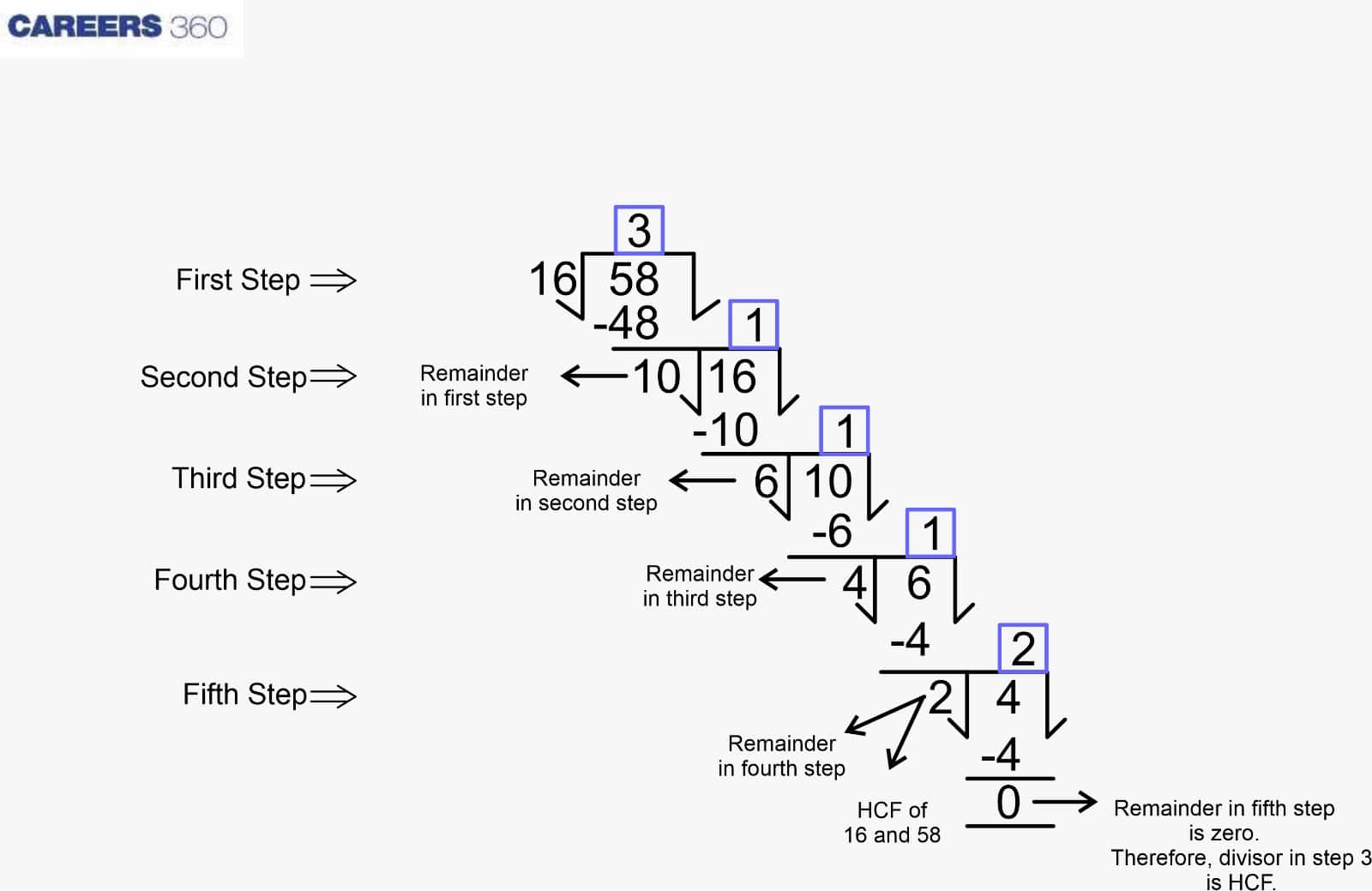
As shown in the figure above, the HCF of 16 and 58 is 2.

LCM: It is the least common multiple, in which the least number exactly divisible by each one of the given numbers is called the LCM of the numbers.
Example: To find the LCM (Least Common Multiple) of 87 and 145
87 = 3 × 29
145 = 5 × 29
The common prime factor is 29
The uncommon prime factors are 3 for 87 and 5 for 145
Thus, the LCM of 87 and 145 = 3 × 5 × 29, which is 435.

Product of Two Numbers = Product of their LCM and HCF

For any two positive integers X and Y,
X × Y = HCF × LCM
Example: For 77 and 99, the HCF is 11 and the LCM is 693
77 × 99 = 7623
11 × 693 = 7623
Therefore,77 × 99 = 11 × 693

Exploring Again the Irrational Numbers

Irrational Numbers: An irrational number is any number that cannot be expressed in the form of pq (where p and q are integers and q≠0).
Examples: √5,π, etc.

Let p be a prime number. If p divides x², then p divides x where x is a positive integer.

Example: 3 divides 9^2, which is equal to 81, which implies that 3 divides 9.
Point to remember:
1) The subtraction or addition of irrational numbers with rational numbers always produces an irrational result.
2) When multiplying or dividing a non-zero irrational number by a rational number produces an irrational outcome is produced.
3) The square root of prime numbers exists as an irrational value. For example, 5 is a prime number, and √5 is irrational. The validity of the above statement depends on Proof by contradiction methods, where we need to execute the following steps to check whether a given statement is correct or incorrect.

Proof by Contradiction: In this method of proof by contradiction, we have to check whether a given statement is correct or incorrect.
(I) We start our explanation with the premise that the statement is true.
(II) By reaching an inconsistent result, we prove that our initial assumption was incorrect.
Example: Prove that √5 is irrational.
Now, let’s assume that √5 is rational.
Since it is rational,√5 can be expressed as
√5 = ab,
where a and b are co-prime Integers, b≠0.
On squaring, a2b2 = 5
⇒ a² = 5b².
Thus, 5 divides a. Then, there exists a number c such that a = 5c. Then, a² = 25c². Thus, 5b² = 25c² or b² = 5c².
Therefore, 5 divides b. The number 5 acts as a common factor in both the expressions of a and b. The proof contradicts our assumption about a and b being co-prime integers.

Exploring Again the Rational Numbers and Their Decimal Expansions

Rational Numbers: These are the numbers that are any real
number and can be expressed in the form pq of R where the denominator q≠0. It is represented by "Q". It is noted that every integer number is a rational number.
Example: 12, 34, −78, 0.3333..., etc.

Terminating Decimals: Terminating decimals are those decimals which end at a specific point. It is also known as finite decimals.
Example: 0.87, 82.25, 9.527, etc.

Non-terminating Decimals: are those decimals where the digits after the decimal point are repeated continuously and infinitely.
Example: 0.142857142857….., 0.3333…., 0.111… etc.

Non-terminating decimals are further divided into parts :

a) Recurring – In this decimal fraction number or group of numbers is repeated indefinitely.
Example: 0.142857142857…

b) Non-recurring – In this, a decimal number continues without any repetition pattern of digits..
Example: 3.1415926535…

Determine if a Given Rational Number is Terminating or Not

If xy is a rational number, and they are satisfies the following conditions, then its decimal expansion would terminate:
a) The HCF of x and y should be 1.
b) y can be represented as a prime factorisation of 2 and 5, i.e. y = 2^a × 5^b, where either a or b, or both, can = 0.
If the prime factorisation of y contains any number other than 2 or 5, then the decimal expansion of that number will be recurring

Example:
150 = 0.02 is a terminating decimal, as the HCF of 1 and 50 is 1, and the denominator (50) can be expressed as 2 × 5².

17 = 0.1428571 is a recurring decimal as the HCF of 1 and 7 is 1, and the denominator (7) is equal to 7¹.

Real Numbers: Previous Year Question and Answer

Question 1:
n² – 1 is divisible by 8 if n is:
(A) an integer
(B) a natural number
(C) An odd integer
(D) An even integer

Solution:
For any even natural number or even integer, n² is always even. So, n² - 1 will always be odd. An odd number can never be divisible by 8.
Therefore, options A, B, and D do not satisfy the given condition.
Now, n² - 1 = (n + 1)(n - 1)
If n is an odd integer,
(n + 1) will be even, and also (n - 1) will be even.
The multiplication of two consecutive even integers is always divisible by 8.
We can understand it through an example:
If n = 3, (n + 1) = 4, (n - 1) = 3 – 1 = 2
So, n²– 1 = 4 × 2 = 8, which is divisible by 8.
Hence, the correct answer is option (C).

Question 2:
Write whether every positive integer can be of the form 4q + 2, where q is an integer. Justify your answer

Solution:
The above statement is not true in all conditions.
For example, if we take the value of q as –1.
Then 4q + 2 = – 4 + 2 = – 2, which is not a positive integer.
Moreover, if q is positive, then 4q + 2 will always be even.
Therefore, we can never write an odd positive number in this form.
Hence, the given statement is false.

Question 3:
Show that the square of any positive integer is either of the form 4q or 4q + 1 for some integer q.

Solution:
Any positive integer can be written in the form of 4m or 4m + 1 or 4m + 2, or 4m + 3.
Case 1:
A=4m
$⇒$(4m)²=16 m²
$=$4(4m²)
$=$4q(Here q=4m²)

Case 2:
A=4m+1
$=$(4m+1)²=(4m)² + 1 + 8m
$=$16m²+8m+1
$=$4(4m²+2m) + 1
$=$4q+1 (here q=4m²+2m)

Case 3:
A = 4m + 2
$=$(4m + 2) ²
$=$16 m² + 4 + 16 m
$=$4 × (4m² + 1 + 4 m)
$=$4q
Here q = (4m² + 1 + 4m)

Case 4:
A = 4m + 3
(4m + 3)² = 16 m² + 9 + 24 m
$=$ 4(4m² + 6m + 2) + 1
$=$ 4q + 1
Here q = (4m² + 6m +2)

Hence square of any positive integer is either of the form 4q or 4q + 1.

Class 10 Chapter Wise Notes

We at Careers360 compiled all the NCERT class 10 Maths notes in one place for easy student reference. The following links will allow you to access them.

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10
• NCERT Syllabus for Class 10