Areas Related to Circles Class 10th Notes - Free NCERT Class 10 Maths Chapter 12 Notes - Download PDF

Class 10 Areas Related to Circles Notes PDF – Download Free Study Material

Students who wish to access the Areas Related to Circles Class 10 Maths notes can click on the link below to download the entire notes in PDF.

Download PDF

Areas Related to Circles Class 10 Notes

Careers360 has prepared these Class 10 Areas Related to Circles Notes to make your revision smoother and faster.

Area of Circle

A circle's area denotes the complete space located between its defining boundaries.

To calculate the Area of a Circle, the formula is:

Area = $πr^2$

(where $r$ is radius)

For Example, find the area of a circle with a radius of 14 cm.

Area of a circle = $πr^2$ = $\frac{22}{7} $ × 14 × 14 = 616 cm²

Circumference of Circle

A circle's circumference represents the complete length of its boundary line. It is also known as the perimeter of the circle.

To calculate the Circumference of a Circle, the formula is:

Circumference = $2πr$
(where $r$ is radius)

For Example, find the circumference of a circle with a radius of 14 cm.

Circumference of a Circle = $2πr$ = 2 × $\frac{22}{7}$ × 14 = 88 cm.

Sector

The portion (or part) of the circular region enclosed by two radii and the corresponding arc is called a sector of the circle.

Types of Sectors

Minor Sector: If the minor arc of the circle forms part of the sector's boundary, it is called a minor sector, which means the smaller area of the circle enclosed by two radii.

Major Sector: If the major arc of the circle is part of the sector's boundaries, it is called a major sector, which means the larger area of the circle enclosed by two radii.

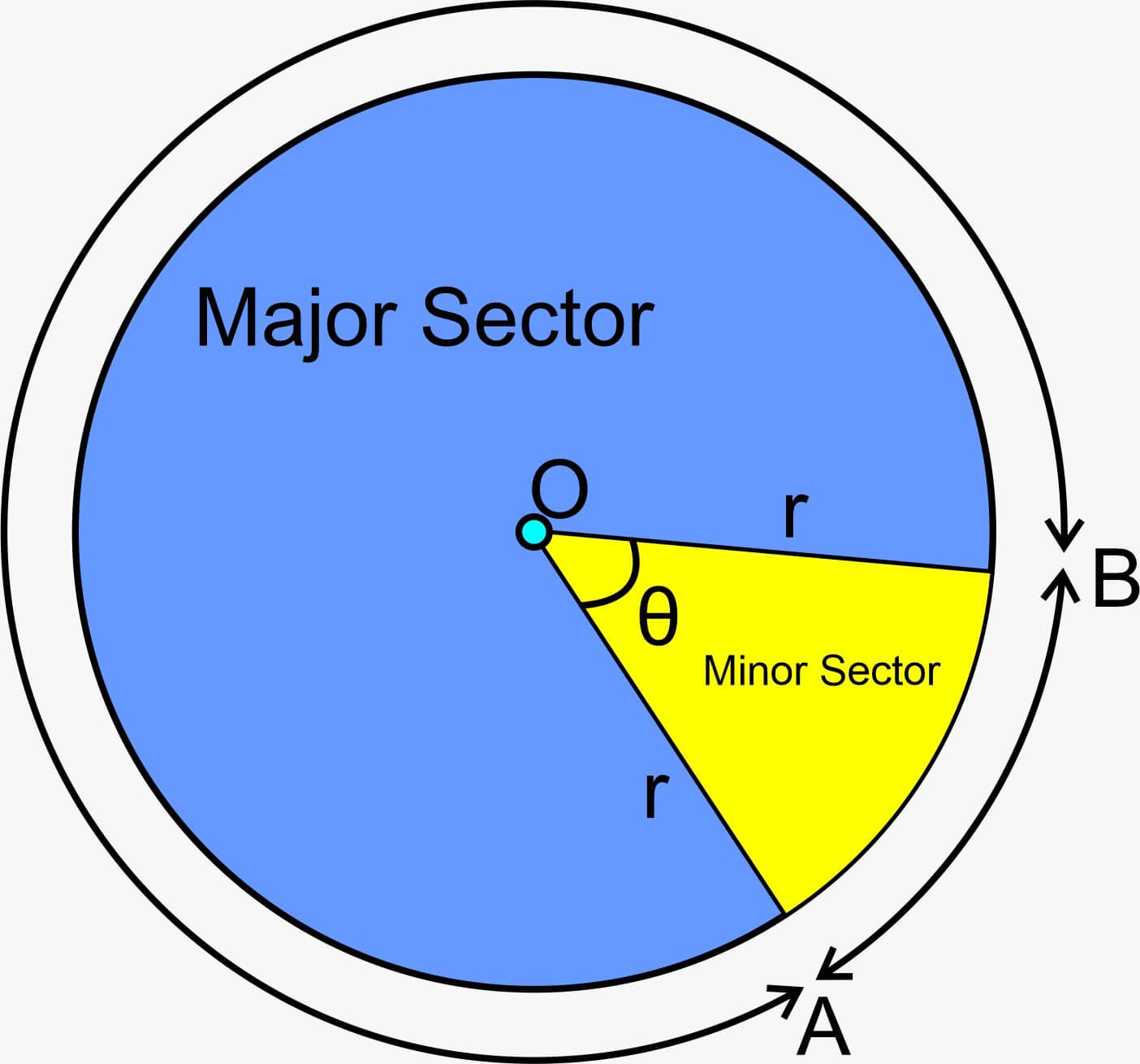
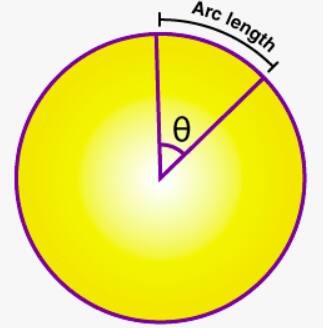
Angle of a Sector

The angle of a sector emerges as the central angle which forms between the two radii within the sector and extends from the circle centre. The size of the sector depends on its central angle and is measured in degrees (°) or radians. $\theta$ shown in the upper figure is the angle of a sector.

Area of a Sector of a Circle

The area of the sector equates to the region that the sector occupies within the circle's boundaries. A sector takes up part of the circle's overall space.
To calculate the Area of a sector of a Circle, the formula is:

Area = $ \frac{\theta}{360} × πr^2 $

(where $ \theta$ is angle of the sector and $ r$ is radius)

For Example, find the area of the sector if the angle of the sector is 90° and the radius of the circle is 14 cm.

Area of the sector
= $ \frac{\theta}{360} × πr^2 $
= $ \frac{90}{360} × \frac{22}{7} × 14^2 $
= $\frac{1}{4}$ × 22 × 14 × 2
= 154 cm²

Length of an Arc of a Sector

The curved sector boundary, which is a component of the circle's circumference, is known as the arc length.

To calculate the Area of a sector of a Circle, the formula is:

Length of an Arc = $ \frac{\theta}{360} × 2πr $

(where $ \theta$ is angle of the sector and $ r$ is radius)

For Example, find the length of the sector if the angle of the sector is 90° and the radius of the circle is 14 cm.

Length of the sector
= $ \frac{\theta}{360}$ × 2πr
= $ \frac{90}{360}$ × 2 × $\frac{22}{7}$ × 14
= $\frac{1}{4}$ × 2 × 22 × 2
= 22 cm²

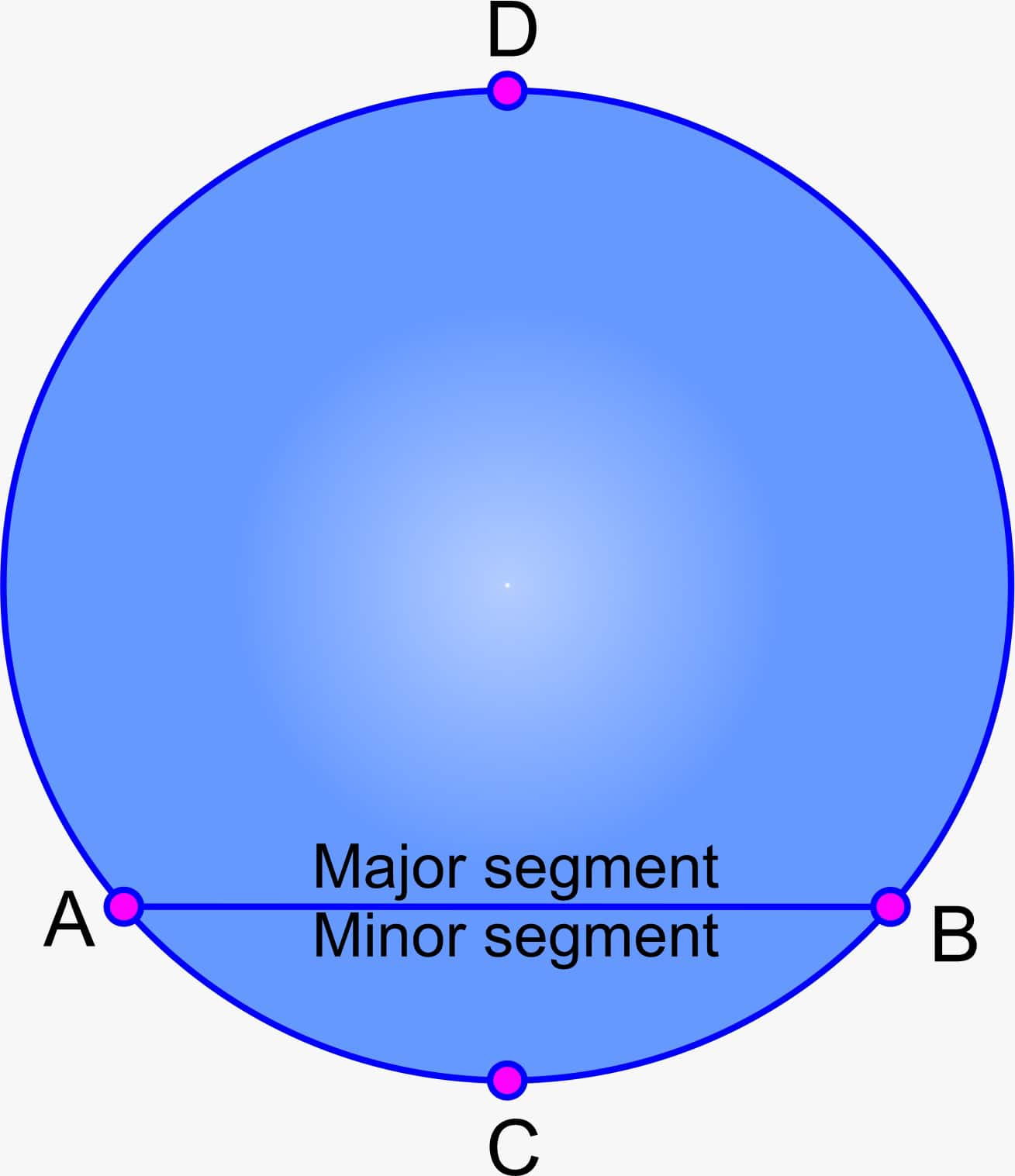
Segment

The area of a circle that is bounded by a chord and its matching arc is called a segment. The centre is not included.

Types of Segments

Minor Segment: The smaller region of the circle cut off by the chord.

Major Segment: The larger region of the circle cut off by the chord.

Area of Segment

To calculate the Area of a segment of a Circle, the formula is:

Area of the segment of a circle = Area of the corresponding sector – Area of the corresponding triangle.

For Example, A circle has a radius of 14 cm, and a chord subtends a 90° angle at the centre. Find the area of the minor segment of the circle.

First, calculate the area of the sector:

Area of a sector
= $ \frac{\theta}{360} × πr^2 $
= $ \frac{90}{360} × \frac{22}{7} × 14^2 $
= $\frac{1}{4}$ × 22 × 14 × 2
= 154 cm²

Now, calculate the area of the triangle:

Since the angle is 90°, the triangle formed is a right-angled triangle with base and height equal to the radius (14 cm each). The formula for the area of a triangle is:

Area = $\frac12$ × base × height

So, area = $\frac12$ × 14 × 14 = 98 cm²

Area of the minor segment = Area of the sector - Area of the Triangle

So, Area of the minor segment = 154 - 98 = 56 cm²

How to Use the Areas Related to Circles Class 10 Notes Effectively?

In Class 10, the Areas Related to Circles chapter teaches us how to find areas of circles, sectors and segments, which is useful in many geometry problems. When we understand the formulas well and know when to apply them, questions become much more manageable. Using Class 10 Maths Chapter 11 notes effectively can make our preparation smooth and clear. Here are some more points on how these notes are important.

• Start by revising basic circle formulas, then move to sectors and segments using examples to build confidence.
• Make a separate list of formulas for quick revision so you do not forget them during practice or before exams.
• ● While solving exercises, use the NCERT Class 10 Maths Chapter 11 notes to understand how a formula is applied in real questions.
• Keep your NCERT Class 10 Maths chapter 11 notes neat and revised regularly, as these concepts are also useful in higher classes and advanced geometry topics.

Areas Related to Circles Class 10 Notes: Previous Year Question and Answer

Listed below are important previous year question answers for NCERT Class 10 Maths Chapter 11 Areas Related to Circles, compiled from different board exams.

Question 1:
Find the area of the circle whose circumference is 22 cm.

Solution:
Let the radius of the circle be $r$.
Circumference of a circle = 22 cm
⇒ $2\pi r = 22$
⇒ $2 \times \frac{22}{7} \times r = 22$
⇒ $2r = 7$
⇒ $r = \frac{7}{2}\ \text{cm}$
Area of the circle $=\pi r^2=\frac{22}{7}\times\frac{7}{2}\times \frac{7}{2}=38.5\ \text{cm}^2$
Hence, the correct answer is 38.5 cm².

Question 2:
Find the length of the arc whose central angle is 45° and the radius of the circle is 28 cm.

Solution:
Given:
Central angle = 45°
The radius of the circle = 28 cm
Length of the arc = $2\pi r×\frac{\theta}{360°}$, where $r$ = radius of the circle, $\theta$ = central angle
= $2×\frac{22}{7}×28×\frac{45°}{360°}$
= $22\ \text{cm}$
Hence, the correct answer is 22 cm.

Question 3:
A chord of length 7 cm subtends an angle of $60^{\circ}$ at the centre of a circle. What is the radius (in cm) of the circle?

Solution:

Since a chord subtends the angle at the centre, the other angles of the triangle formed by the chord and the centre will be the same as two sides opposing. It will be the same because both are radii of the circle.
Let the other two angles be x.
We know that,
The sum of the angles of the triangle = 180$^\circ$
⇒ 60$^\circ$ + x + x = 180$^\circ$
⇒ 2x = 120$^\circ$
⇒ x = 60$^\circ$
$\therefore$ All angles are 60$^\circ$ (equilateral triangle)
$\therefore$ Radius of triangle = side of triangle = 7 cm
Hence, the correct answer is $7$ cm.

NCERT Class 10 Maths Notes – Chapter-Wise Links

To support students' preparation, Careers360 has compiled all Class 10 Maths NCERT Notes here for quick and convenient access.

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science.

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science Solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

As students step into a new class, they must first explore the latest syllabus to identify the chapters included. Below are the links to the most recent syllabus and essential reference books.

• NCERT Books Class 10 Maths
• NCERT Books for Class 10 Science
• NCERT Syllabus Class 10 Maths
• NCERT Books Class 10
• NCERT Books for Class 10 English
• NCERT Syllabus Class 10