NCERT Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Notes - Download PDF Notes

Linear equations using two variables serve as key components of algebraic mathematics structures because they help solve problems which require solutions for two unknown factors. The relationship between two variables becomes established through basic mathematical operations such as addition and subtraction, as well as multiplication. Linear equations consist of a single degree value, thus all variables possess an exponent value of 1. The equations produce straight lines which appear on coordinate planes during graphical representation.

This Story also Contains

1. NCERT Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables: Notes
2. Equation:
3. Linear Equation:
4. Ways to Find the Solutions of Linear Equations:
5. Class 10 Chapter Wise Notes

Engineers from multiple backgrounds, including physics and mathematics, together with economics and computer science and mathematics make extensive use of these equations when addressing real-world problems. Three main methods exist to solve these problems: graphical representation and substitution, as well as elimination, which allow students to find solutions via structured methods. The NCERT class 10th maths notes comprehensively cover all the topics, sub-topics, short tricks, formulae, and other important key points. Students must read all the topics of class 10 to ace the subjects from the NCERT notes.

NCERT Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables: Notes

Equation:

When two mathematical expressions and one or more variables are set equal to each other, this relationship becomes an equation.

Examples: x + 5 = 10, x² – 4x + 4 = 0, x³ – 3x² + 2x = 0

Linear Equation:

Linear equations exist when all involved variables have their power set equal to one. Linear equations always maintain a degree value of 1.
The general form of a linear equation is ax + b = 0
Examples: 2x + 3 = 7, 5y – 4 = 16

General Form of a Linear Equation in Two Variables:

Linear equations written in standard form appear as ax + by + c = 0 with the conditions that neither a nor b equals zero.

Examples: 2x + 3y = 6, x – 4y = 8

Convert the Word Problem into a Proper Linear Equation:

Steps to convert:

1. Variables should represent unidentified qualities found in the problem.
2. Write mathematical expressions to show quantity relationships, then substitute unknown values with variables.

Example: A bookstore sells notebooks and pens. The total cost of 4 notebooks and 3 pens is Rs. 22. The total cost of 2 notebooks and 5 pens is Rs. 18. Write a system of linear equations to represent this situation.

Identify Variables: Need to define variables for the unknown quantities, which are cost.

• Represent the cost of one notebook (in rupees).
• Represent the cost of one pen (in rupees).

Write Mathematical Expressions: Now, we express the given relationships as equations:

• The total cost of 4 notebooks and 3 pens is Rs. 22: 4x + 3y = 22
• The total cost of 2 notebooks and 5 pens is Rs. 18: 2x + 5y = 18

Ways to Find the Solutions of Linear Equations:

There are two ways to solve the linear equations, that are:

1. Graphical Method
2. Algebraic Method

Graphical Method:

A pair of linear equations becomes solvable through the graphical method, which transforms them into straight lines on a coordinate plane. Evaluation of the lines at their intersection points determines the solutions for the given equations. To solve equations graphically:

1. Plot the equations on the Cartesian Plane
2. Analyze the intersection:

• The lines intersect at a single point. In this case, the pair of equations has a unique solution.
• The parallel lines. In this case, the equations have no solution.
• The coincident lines. In this case, the equations have infinitely many solutions.

Important Concepts:

• A pair of linear equations which has no solution is called an inconsistent pair of linear equations.
• A pair of linear equations in two variables, which has one solution, is called a consistent pair of linear equations.
• A pair of linear equations which are equivalent has infinitely many distinct common solutions. Such a pair is called a dependent and consistent pair of linear equations in two variables.

Types of Intersection:

There are three possibilities for the Intersection of a pair of straight lines on a plane:

1) Intersect at a single point

2) They are parallel

3) They are coincidental

1. Intersect at a single point:

Suppose that there are two lines are given as
ax + by + c = 0
dx + ey + f = 0
Then these two lines intersect only if
ad≠be≠cf

Example:
x + y = 1
y = x

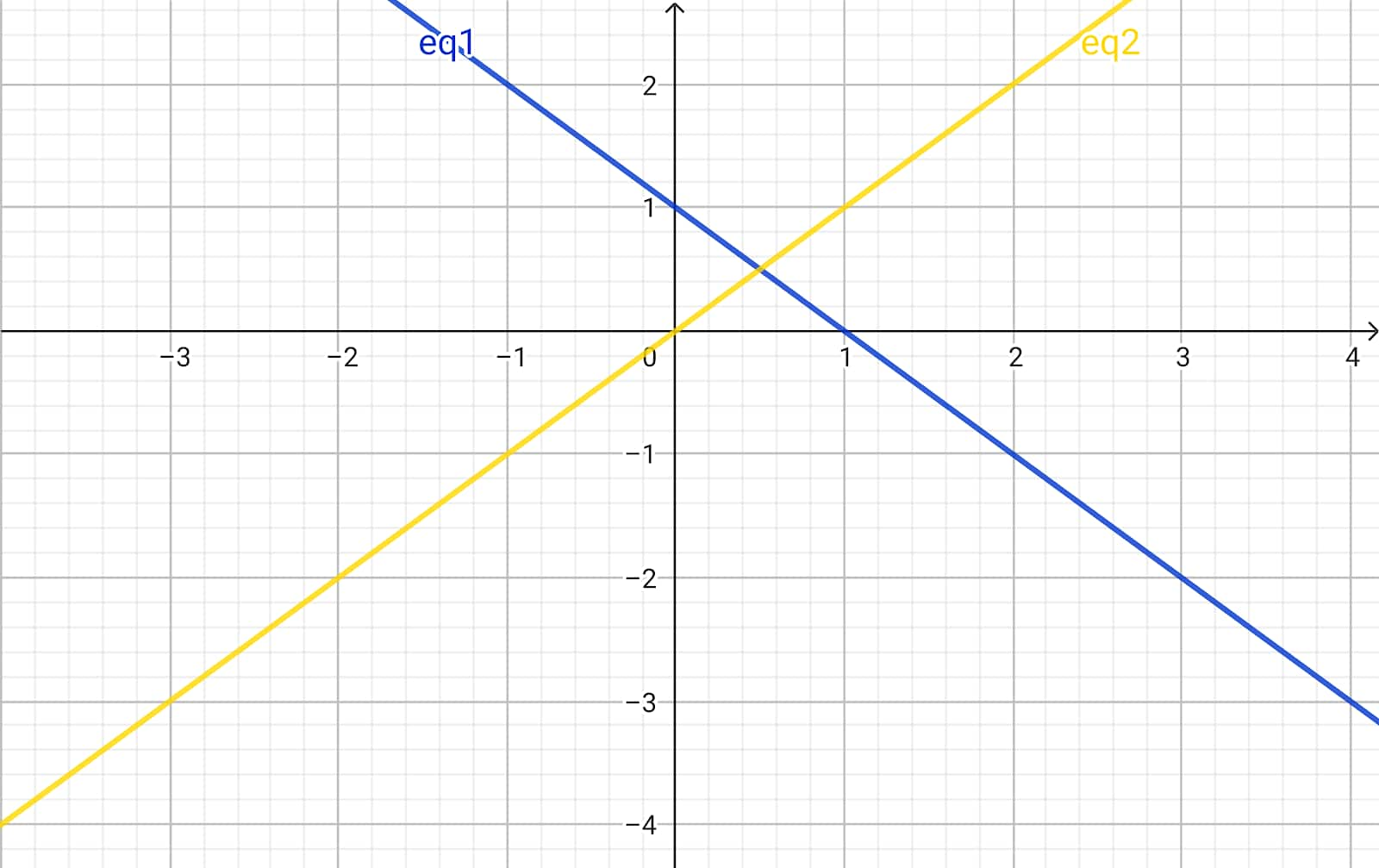
In this case, the pair of equations has a unique solution and thus is called a consistent pair of linear equations.

2. They are parallel:

Suppose that there are two lines are given as
ax + by + c = 0
dx + ey + f = 0
Then these two lines are parallel only if
ad≠be=cf

Example:
x + y = 1
x + y = 2

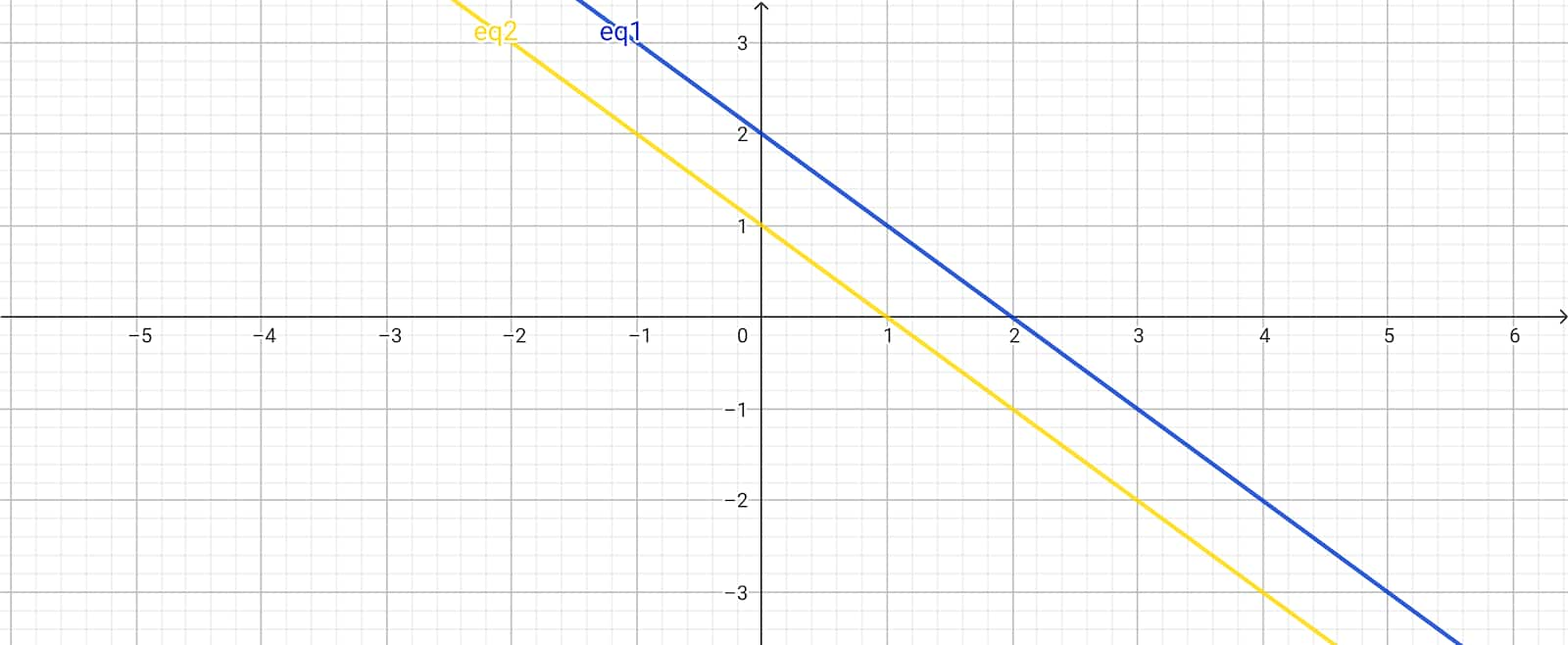
A pair of linear equations has no solution and thus is called an inconsistent pair of linear equations.

3. They are coincidental:

Suppose that there are two lines are given as
ax + by + c = 0
dx + ey + f = 0
Then these two lines coincide only if
ad=be=cf

Example:
x + y = 1
y + x = 1

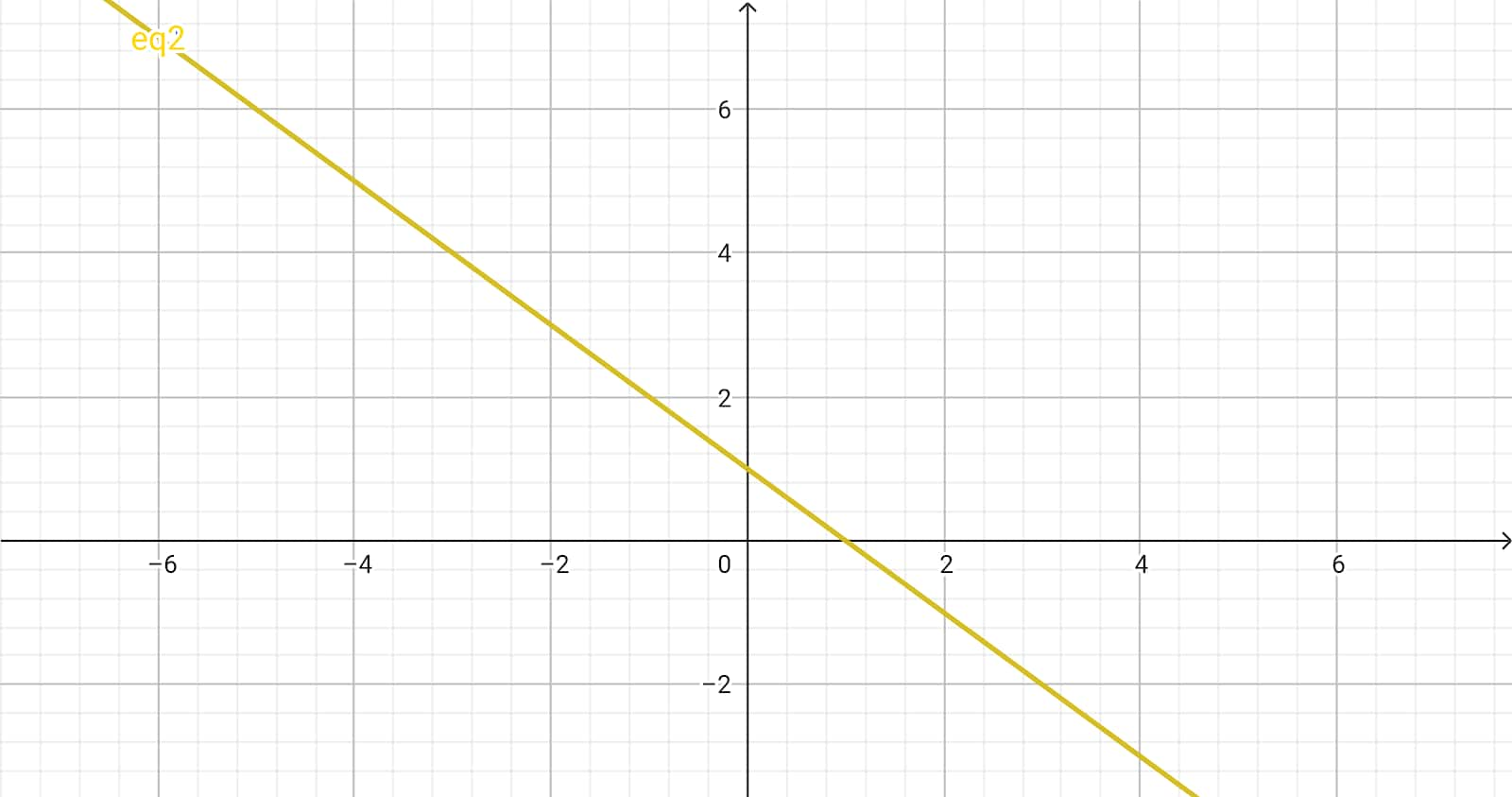
A pair of linear equations is equivalent and has infinitely many distinct common solutions, and thus such a pair is called a dependent and consistent pair of linear equations in two variables.

Table:

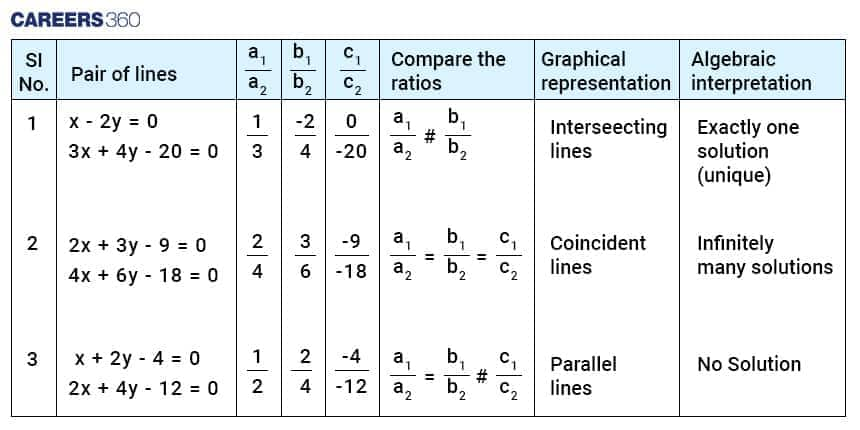
Observation: If the lines represented by the equation;
ax + by + c = 0 and,
dx + ey + f = 0
Are, (i) Intersecting then, ad≠be≠cf

(ii) parallel then, ad≠be=cf

(iii) coincident then, ad=be=cf

Problems with Graphical Method:

1. Not Always Accurate:
The task of creating perfect straight lines through graph paper proves challenging for most people. Small plotting errors or misdrawn lines make it possible to arrive at incorrect solutions.

2. Difficult for Complex Values:
The exact point of intersection is hard to determine when the solution involves fractional or decimal values (e.g. x = 2.73).

3. Takes More Time:
The process of plotting two equations followed by line drawing before locating the intersection takes up more time.

4. Not Practical for Large Numbers:
The process of graphing points from large numbers (such as 235x + 578y = 3467 ) effectively becomes impracticable when performed on a graph.

Algebraic Method:

Due to the issues of the Graphical Method, Algebraic Methods were introduced and helped to provide accurate solutions. There are two types of Algebraic methods:

• Substitution Method
• Elimination Method

Substitution Method:

Substitute the value of one variable by expressing it in terms of the other variable to solve the pair of linear equations.

Steps to solve linear equations by the substitution method:

1. Find the value of a variable, say y, described in terms of another variable x through either available equation, whichever is convenient.
2. Substitute this value of y with the variable in the second equation to make the equation in one variable, and it can be solved now.
3. The result obtained from Step 2 should be used to replace x (or y) within the equation from Step 1, leading to the value of another variable.

Example:
The pair of linear equations:
7x – 15y = 2
x + 2y = 3

Solution:
Step 1: Pick either of the equations and write one variable in terms of the other.
Let us consider Equation (2):
x + 2y = 3
and write it as x = 3 – 2y
Step 2: Substitute the value of x in Equation (1) i.e. 7x – 15y = 2
7(3 – 2y) – 15y = 2
After solving the equation, get the value of y
21 – 14y – 15y = 2
– 29y = –19
y = 1929

Step 3: Substituting this value of y in the Equation we get from step 1, we get
x = 3 – 2( 1929)
x = 4929

4929

Points to remember:

• If, while solving the equation in step 2, we end up with a true statement like 0 = 0, the equations represent the same lines or coincident lines, which means infinitely many solutions.
• If, while solving the equation in step 2, we end up with a false statement like 8 = 7, the equations represent the parallel lines, which means no solution.

Elimination Method:

Eliminate one variable first to get a linear equation in one variable.

Steps to solve linear equations by the elimination method:

1. Begin by multiplying each equation by appropriate non-zero constants that make the x or y coefficients match numerically.
2. Then add or subtract one equation from the other so that one variable gets eliminated.
3. Solve the equation by reducing it to one variable and obtain its value.
4. Substitute the obtained value of x (or y) into any of the original equations to determine the value of another variable.

Example: The pair of linear equations:
9x – 4y = 2000
7x – 3y = 2000

Solution:
Step 1: To make the coefficients of one variable equal, multiply Equation (1) by 3 and Equation (2) by 4,
27x – 12y = 6000
28x – 12y = 8000
Step 2: Subtract the equations to eliminate y, because the coefficients of y are the same.
(28x – 27x) – (12y – 12y) = 8000 – 6000
Step 3: Solve the equation:
28x – 27x = 2000
x = 2000
Step 4: Substituting this value of x in given equation i.e. 9x – 4y = 2000, to get the value of y:
9(2000) – 4y = 2000
i.e., y = 4000

Points to remember:

• If in Step 2, we obtain a true statement involving no variable, then the original pair of equations has infinitely many solutions.
• If in Step 2, we obtain a false statement involving no variable, then the original pair of equations has no solution, i.e., it is inconsistent.

Class 10 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10
• NCERT Syllabus for Class 10