NCERT Exemplar Class 10 Maths Solutions Chapter 3 - Pair of Linear Equations in Two Variables

Question 1

Choose the correct answer from the given four options:Graphically, the pair of equations 6x – 3y + 10 = 0, 2x – y + 9 =0 represents two lines which are
(A) intersecting at exactly one point.
(B) intersecting at exactly two points.
(C) coincident.
(D) parallel.

Answer:

Answer: D
Solution:
In equation
6x – 3y + 10 = 0
a₁ = 6, b₁ = –3, c₁ = 10
In equation
2x – y + 9 = 0
a₂ = 2, b₂ = –1, c₂ = 9
$\frac{a_{1}}{a_{2}}= \frac{6}{2}= 3$
$\frac{b_{1}}{b_{2}}= \frac{-3}{-1}= 3$

$\Rightarrow$$\frac{c_{1}}{c_{2}}= \frac{10}{9}$
Here, $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
The lines are parallel.

Question 2

The pair of equations x + 2y + 5 = 0 and –3x – 6y + 1 = 0 have
(A) a unique solution
(B) Exactly two Solutions
(C) infinitely many Solutions
(D) no solution

Answer:

Answer: D
Solution:
In equation
x + 2y + 5 = 0
a₁ = 1, b₁ = 2, c₁ = 5
In equation
–3x –6y + 1 = 0
a₂ = –3, b₂ = –6, c₂ = 1
$\frac{a_{1}}{a_{2}}= \frac{1}{-3}$
$\frac{b_{1}}{b_{2}}= \frac{2}{-6}= \frac{-1}{3}$
$\frac{c_{1}}{c_{2}}= \frac{5}{1}= 5$
Here $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
Hence, these lines are parallel to each other and have no solution.

Question 3

If a pair of linear equations is consistent, then the lines will be
(A) parallel
(B) always coincident
(C) intersecting or coincident
(D) always intersecting

Answer:

Answer: C
Solution:

If the pair of linear equations is consistent, then they have unique or infinitely many Solutions.
In unique solution, $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$
Lines are intersecting
In infinitely many solutions,
$\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
Lines are coincident
Hence, the pair of lines is intersecting or coincident.

Question 4

The pair of equations y = 0 and y = –7 has
(A) one solution
(B) two Solutions
(C) infinitely many Solutions
(D) no solution

Answer:

Answer: D
Solution:

Lines y = 0 and y = –7 are parallel to each other.
Hence, they never intersect. Hence, the pair of equations has no solution.

Question 5

The pair of equations x = a and y = b graphically represents lines which are
(A) parallel
(B) intersecting at (b, a)
(C) coincident
(D) intersecting at (a, b)

Answer:

Answer: D
Solution:

The lines x = a and y = b intersect at (a, b)

Question 6

For what value of k, do the equations 3x – y + 8 = 0 and 6x – ky = –16 represent coincident lines?
(A) $\frac{1}{2}$
(B) –$-\frac{1}{2}$
(C) 2
(D) –2

Answer:

Answer: C
Solution:
Equations are
3x – y + 8 = 0
6x – ky + 16 = 0
In equation
3x – y + 8 = 0
a₁ = 3, b₁ = –1, c₁ = 8
In equation
6x – ky + 16 =0
a₂ = 6, b₂ = –k, c₂ = 16
$\frac{a_{1}}{a_{2}}= \frac{3}{6}= \frac{1}{2}$
$\frac{b_{1}}{b_{2}}= \frac{-1}{-k}= \frac{1}{k}$
$\frac{c_{1}}{c_{2}}= \frac{8}{16}= \frac{1}{2}$
Since lines are coincident
Hence, $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
$\frac{1}{2}= \frac{1}{k}= \frac{1}{2}$….(i)
1/k = 1/2 ( from equation (1))
k = 2
Hence, the value of k is 2.

Question 7

If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is
(A)$\frac{-5}{4}$
(B)$\frac{2}{5}$
(C)$\frac{15}{4}$|
(D)$\frac{3}{2}$

Answer:

Answer: C
Solution:
Equations are
3x + 2ky = 2
2x + 5y + 1 = 0
In equation
3x + 2ky – 2 = 0
a₁ = 3, b₁ = 2k, c₁ = –2
In equation
2x + 5y + 1 = 0
a₂ = 2, b₂ = 5, c₂ = 1
$\frac{a_{1}}{a_{2}}= \frac{3}{2}$
$\frac{b_{1}}{b_{2}}= \frac{2k}{5}$
$\frac{c_{1}}{c_{2}}= \frac{-2}{1}=-2$
Since lines are parallel
Hence,
$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq\frac{c_{1}}{c_{2}}$
$\frac{3}{2}=\frac{2k}{5}\neq-2$ ……(1)
$\frac{3}{2}=\frac{2k}{5}$ ( from equation (1))
$2k=\frac{15}{2}\Rightarrow k=\frac{15}{4}$
Hence, the value of k is $\frac{15}{4}$ .

Question 8

The value of c for which the pair of linear equations cx – y = 2 and 6x – 2y = 3 will have infinitely many Solutions is
(A) 3
(B) – 3
(C) –12
(D) no value

Answer:

Answer: D
Solution:
Equations are
cx – y – 2 = 0, 6x – 2y – 3 = 0
In equation
cx – y – 2 = 0
a₁ = c, b₁ = –1, c₁ = –2
In equation
6x – 2y – 3 = 0
a₂ = 6, b₂ = –2, c₂ = –3
Since equations have infinitely many Solutions
Hence, $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
$\frac{c}{6}= \frac{-1}{-2}\neq \frac{-2}{-3}$
Here we find that $\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$ i.e., equations are inconsistent
So, we can not assign any value to c.

Question 9

One equation of a pair of dependent linear equations is –5x + 7y = 2. The second equation can be
(A) 10x + 14y + 4 = 0
(B) –10x – 14y + 4 = 0
(C) –10x + 14y + 4 = 0
(D) 10x – 14y = –4

Answer:

Answer: D
Solution:
Given equation is
–5x + 7y – 2 = 0
a₁ = –5, b₁ = 7, c₁ = –2
For a dependent linear equation
$\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}= \frac{1}{k}$
$\frac{-5}{a_{2}}= \frac{7}{b_{2}}= \frac{-2}{c_{2}}= \frac{1}{k}$
a₂ = –5k, b₂ = 7k, c₂ = –2k
Put k = 2
a₂ = –10, b₂ = 14, c₂ = –4
The revived equation is of the type a₂x + b₂y + c₂ = 0
Put a₂ = – 10, b₂ = 14, c₂= –4
–10x + 14y – 4 = 0
10x – 14 y = –4

Question 10

A pair of linear equations which has a unique solution x = 2, y = –3 is
(A) x + y = –1 ; 2x – 3y = –5
(B) 2x + 5y = –11 ; 4x + 10y = –22
(C) 2x – y = 1 ; 3x + 2y = 0
(D) x– 4y –14 = 0 ; 5x – y – 13 = 0

Answer:

Answer: B, D
Solution:
A pair which have unique solution x = 2, y = –3 will satisfy L.H.S. = R.H.S. if we put x = 2 and y = –3
Put x = 2, y = –3 in option (A)
x + y = –1 ; 2x – 3y = –5
2 – 3 = –1 ; 2(2) – 3 (–3) = –5
–1 = –1 (True) ; 4 + 9 = –5
13 = – 5 (False)
Put x = 2, y = –3 in option (B)
2x + 5y = –11 ; 4x + 10y = –22
2(2) + 5(–3) = –11 ; 4(2) + 10 (–3) = –22
4 – 15 = –11 ; 8 – 30 = –22
–11 = –11 (True) –22 = –22 (True)
Put x = 2, y = – 3 in option (C)
2x – y = 1 ; 3x + 2y = 0
2(2) – (–3) = 1 ; 3(2) + 3 (–3) = 0
4 + 3 = 1 ; 6 – 6 = 0
7 = 1 (False) ; 0 = 0 (True)
Put x = 2, y = – 3 in option (D)
x – 4y – 14 = 0 ; 5x – y – 13 = 0
2 – 4 (–3) – 14 = 0 ; 5(2) – (–3) – 13 = 0
2 + 12 – 14 = 0 ; 10 + 3 – 13 = 0
0 = 0 (True) ; 13 – 13 = 0
0 = 0 (True)
By putting the value of x = 2, y = –3 in A, B, C, D; two options B, D satisfy L.H.S = R.H.S
Hence, both (B, D) are correct

Question 11

If x = a, y = b is the solution of the equations x – y = 2 and x + y = 4, then the values of a and b are, respectively
(A) 3 and 5
(B) 5 and 3
(C) 3 and 1
(D) –1 and –3

Answer:

Answer : (C)
Solution:
Equation are x – y = 2 … (1)
x + y = 4 … (2)
Add equations (1) and (2)
x – y = 2
x + y = 4
$\Rightarrow$2x = 6
$\Rightarrow$x = 3
Put x = 3 in equation (2)
$\Rightarrow$3 + y = 4
$\Rightarrow$y = 4 – 3
$\Rightarrow$y = 1
it is given that a = x, b = y
Hence, a = 3, b = 1

Question 12

Aruna has only Rs 1 and Rs 2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is Rs 75, then the number of Rs 1 and Rs 2 coins are, respectively
(A) 35 and 15
(B) 35 and 20
(C) 15 and 35
(D) 25 and 25

Answer:

Answer:(D) 25 and 25
Solution:
Let Rs. 1 coins = x
Rs. 2 coins = y
As per the Question
x + y = 50 …(1)
x + 2y = 75 … (2)
Find the value of x, y using the elimination method.
x + y = 50
x + 2y = 75
y = 25 (subtract equation 1 from equation 2)
Put y = 25 in equation (1)
$\Rightarrow$x + 25 = 50
$\Rightarrow$x = 25
x = 25, y = 25
Hence, Rs. 1 coins = 25
Rs. 2 coins = 25

Question 13

The father’s age is six times his son’s age. Four years Hence, the age of the father will be four times his son’s age. The present ages, in years, of the son and the father are, respectively
(A) 4 and 24
(B) 5 and 30
(C) 6 and 36
(D) 3 and 24

Answer:

Answer:(C) 6 and 36
Solution:
According to the questions, at present father’s age is six times than son’s age.
Let son's age = x
Father age = y
y = 6x … (1)
After 4 years, Father’s age will be four times than son’s age. That is
$\Rightarrow$y + 4 = 4 (x + 4)
$\Rightarrow$y + 4 = 4x + 16
4x – y + 12 = 0 …(2)
Put y = 6x in equation (2)
4x – 6x + 12 = 0
+ 2x = + 12
x = $\frac{12}{2}$ = 6
Put x = 6 in equation (1)
$\Rightarrow$y = 6 (6) = 36
$\Rightarrow$y = 36
Hence, present age of the father is 36, and the son is 6.

Question 1

Do the following pair of linear equations have no solution? Justify your answer.

(i) 2x + 4y = 3 ; 12y + 6x = 6
(ii) x = 2y; y = 2x
(iii) 3x + y – 3 = 0 ;$2x+\frac{2}{3}y= 2$

Answer:

(i)Solution:
Equations are 2x + 4y = 3
12y + 6x = 6
In equation 2x + 4y – 3 = 0
a₁ = 2, b₁ = 4, c₁ = –3
In equation 12y + 6x – 6 = 0
a₂ = 6, b₂ = 12, c₂ = –6
$\frac{a_{1}}{b_{2}}= \frac{2}{6}= \frac{1}{3},\frac{b_{1}}{b_{2}}= \frac{4}{12}= \frac{1}{3},\frac{c_{1}}{c_{2}}= \frac{-3}{-6}= \frac{1}{2}$
For no solution $\frac{a_{1}}{b_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$ also, Here we have $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$

Hence, the given equation has no solution.
(ii)Solution:
Equations are x – 2y = 0
–2x + y = 0
In equation
x – 2y = 0
a₁ = 1, b₁ = –2, c₁ = 0
In equation
–2x + y = 0
a₂ = –2, b₂ = 1, c₂ = 0
$\frac{a_{1}}{b_{2}}= \frac{1}{-2},\frac{b_{1}}{b_{2}}= \frac{-2}{1}= \frac{c_{1}}{c_{2}}= \frac{0}{0}$
For no solution but$\frac{a_{1}}{b_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$ here

$\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
Hence, the given pair of equations has a unique solution.
(iii)Solution:
Equations are 3x + y = 3
$2x+\frac{2}{3}y= 2$
In equation
3x + y – 3 = 0
a₁ = 3, b₁ = 1, c₁ = –3
In equation
$2x+\frac{2}{3}y-2= 0$
a₂ = 2, b₂= $\frac{2}{3}$, c₂ = –2
$\frac{a_{1}}{b_{2}}= \frac{3}{2},\frac{b_{1}}{b_{2}}= \frac{3}{2}= \frac{c_{1}}{c_{2}}= \frac{-3}{-2}= \frac{3}{2}$
For no solution $\frac{a_{1}}{b_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$ but here
$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
Hence, the given pair of equations has infinitely many Solutions.

Question 2

Do the following equations represent a pair of coincident lines? Justify your answer.

(i)$3x+\frac{1}{7}y= 3$; 7x + 3y = 7
(ii) –2x – 3y = 1 ; 6y + 4x = –2
(iii)$\frac{x}{2}+y+\frac{2}{5}= 0;4x+8y+\frac{5}{6}= 0$

Answer:

(i)Solution:
Equation are 3x + $\frac{1}{7}$y = 3
7x + 3y = 7
In equation
3x + $\frac{1}{7}$y – 3 = 0
a₁ = 3 ; b₁ = $\frac{1}{7}$ ; c₁ = –3
In equation
7x + 3y – 7 = 0
a₂ = 7 ; b₂ = 3; c₂ = –7
$\frac{a_{1}}{a_{2}}= \frac{3}{7};\frac{b_{1}}{b_{2}}= \frac{1}{21};\frac{c_{1}}{c_{2}}= \frac{-3}{-7}= \frac{3}{7}$
For coincident lines $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$ but here $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$
Hence, the given pair of equations does not represent a pair of coincident lines.
(ii)Solution:
Equation are –2x – 3y = 1
4x + 6y = –2
In equation
–2x – 3y – 1 = 0
a₁ = –2 ; b₁ = –3 ; c₁ = –1
In equation
4x + 6y + 2 = 0
a₂ = 4 ; b₂ = 6; c₂ = 2
$\frac{a_{1}}{a_{2}}= \frac{-2}{4}= \frac{-1}{2};\frac{b_{1}}{b_{2}}= \frac{-3}{6}= \frac{-1}{2},\frac{c_{1}}{c_{2}}= \frac{-1}{2}$
For coincident lines $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$ also here $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
Hence, the given pair of equations represents a pair of coincident lines.
Solution: (iii)
Equation are $\frac{x}{2}+y+\frac{2}{5}= 0$
4x + 8y + $\frac{5}{16}$= 0
In equation
$\frac{x}{2}+y+\frac{2}{5}= 0$
a₁ = 1/2 ; b₁ = 1 ; c₁ = $\frac{2}{5}$
In equation
4x + 8y + $\frac{5}{16}$= 0
a₂ = 4 ; b₂ = 8; c₂ = $\frac{5}{16}$
$\frac{a_{1}}{a_{2}}= \frac{1}{8};\frac{b_{1}}{b_{2}}= \frac{1}{8};\frac{c_{1}}{c_{2}}\Rightarrow \frac{2}{5}\times \frac{16}{5}\Rightarrow \frac{32}{25}$
For coincident lines $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$but here $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
Hence, the given pair of equations does not represent a pair of coincident lines.

Question 3

Are the following pair of linear equations consistent? Justify your answer.
(i) –3x– 4y = 12 ; 4y + 3x = 12
(ii)$\frac{3}{5}x-y= \frac{1}{2};\frac{1}{5}x-3y= \frac{1}{6}$ ;
(iii) 2ax + by = a; 4ax + 2by = 2a ; a, b ≠ 0
(iv) x + 3y = 11 ; 4x + 12y = 22

Answer:

Solution: (i)
Equation are : –3x – 4y = 12
4y + 3x = 12
In equation
–3x – 4y – 12 = 0
a₁ = –3; b₁ = –4 ; c₁ = –12
In equation
4y + 3x – 12 = 0
a₂ = 3 ; b₂ = 4; c₂ = –12
$\frac{a_{1}}{a_{2}}= \frac{-3}{3}= -1;\frac{b_{1}}{b_{2}}= \frac{-4}{4}= -1,\frac{c_{1}}{c_{2}}\Rightarrow \frac{-12}{-12}= \frac{1}{1}$
For consistency either $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}or \frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$ but here $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$

Hence, the pair of linear equations is not consistent.
Solution: (ii)
Equation are : $\frac{3}{5} x-y=\frac{1}{2}$
$\frac{1}{5} x-3 y=\frac{1}{6}$
In equation
$\frac{3}{5} x-y=\frac{1}{2}$
a₁= $\frac{3}{5}$; b₁ = –1 ; c₁ = $-\frac{1}{2}$
In equation
$\frac{1}{5} x-3 y=\frac{1}{6}$
a₂ = 1/5 ; b₂ = – 3; c₂ = –1/6
$\frac{a_{1}}{a_{2}}= \frac{3}{5}\times \frac{5}{1}= 3;\frac{b_{1}}{b_{2}}= \frac{-1}{-3}= \frac{1}{3};\frac{c_{1}}{c_{2}}= \frac{-1}{-2}\times \frac{6}{1}= 3$
For consistency either $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}or\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$ also here $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$
Hence, given equations are consistent.
Solution: (iii)
Equation are: 2ax + by = a
4ax + 2by = 2a
In equation
2ax + by – a = 0
a₁ = 2a; b₁ = b; c₁ = –a
In equation
4ax + 2by – 2a = 0
a₂ = 4a ; b₂ = 2b; c₂ = –2a
$\frac{a_{1}}{a_{2}}= \frac{2a}{4a}= \frac{1}{2};\frac{b_{1}}{b_{2}}= \frac{b}{2b}= \frac{1}{2};\frac{c_{1}}{c_{2}}= \frac{-a}{-2a}= \frac{1}{2}$
For consistency either $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}or \frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$
Also, here $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$
Hence, given equations are consistent
Solution: (iv)
Given, equations are x + 3 y = 11
4x + 12y =22
In equation
x + 3y = 11
a₁ = 1; b₁ = 3; c₁ = –11
In equation
4x + 12y = 22
a₂ = 4 ; b₂ = 12; c₂ = –22
$\frac{a_{1}}{a_{2}}= \frac{1}{4} ;\frac{b_{1}}{b_{2}}=\frac{3}{12}= \frac{1}{4};\frac{c_{1}}{c_{2}} = \frac{-11}{-22}= \frac{1}{2}$
For consistency either $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}or \frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$ but here $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
Hence, given equations are not consistent.

Question 4

For the pair of equations $\lambda$x + 3y = –7 ,2x + 6y = 14to have infinitely many Solutions, the value of $\lambda$ should be 1. Is the statement true? Give reasons.

Answer:

Solution:
Here equations are $\lambda$ x + 3y = –7
2x + 6y = 14
a₁ = $\lambda$ , b₁ = 3, c₁ = 7
a₂ = 2, b₂ = 6, c₂ = –14
The equation has infinitely many solutions
$\therefore \frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
$\frac{\lambda }{2}= \frac{3}{6}\neq \frac{-7}{14}$
Here we can see that
$\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
Hence, no value of $\lambda$ exists because it is given that the equation has infinitely many Solutions
Hence, the statement is false.

Question 5

For all real values of c, the pair of equations x– 2y = 8, 5x – 10y = c have a unique solution. Justify whether it is true or false.

Answer:

Solution:
Equation are x – 2y = 8
5x – 10y = c
Here a₁ = 1, b₁ = –2, c₁ = –8
a₂ = 5, b₂ = –10, c₂ = –c
$\frac{a_{1}}{a_{2}}= \frac{1}{5};\frac{b_{1}}{b_{2}}= \frac{-2}{-10}= \frac{1}{5};\frac{c_{1}}{c_{2}}= \frac{-8}{-c}= \frac{8}{c}$
For unique solution $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$ but here $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}$
Hence, the given statement is false.

Question 6

The line represented by x = 7 is parallel to the x–axis. Justify whether the statement is true or not.

Answer:

Solution:

From the above graph, it is clear that x = 7 is not parallel to the x-axis, but it is parallel to the y-axis. Hence, the given statement is false.

Question 1

For which value(s) of $\lambda$ , do the pair of linear equations $\lambda$x + y = $\lambda ^{2}$ and x +$\lambda$y = 1 have
(i) no solution?
(ii) infinitely many Solutions?
(iii) a unique solution?

Answer:

(i)Solution:
The given equations are
$\lambda$x + y =$\lambda ^{2}$ , x + $\lambda$y = 1
In equation
$\lambda$x + y – $\lambda ^{2}$ = 0
a₁ = $\lambda$, b₁ = 1, c₁ = –$\lambda ^{2}$
In equation
x + $\lambda$y – 1 = 0
a₂ =1, b₂ = $\lambda$, c₂ = –1
For no solution $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
$\frac{a_{1}}{a_{2}}= \frac{\lambda }{1}$
$\frac{b_{1}}{b_{2}}= \frac{1}{\lambda }$
$\frac{c_{1}}{c_{2}}= \frac{-\lambda^{2}}{ -1}= \lambda^{2}$
$\Rightarrow$$\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
$\Rightarrow$$\frac{\lambda }{1}= \frac{1}{\lambda}\neq \lambda^{2}$
$\Rightarrow$$\frac{\lambda }{1}= \frac{1}{\lambda}$
$\Rightarrow$$\lambda ^{2}= 1$
$\Rightarrow$$\lambda$=1,-1
Hence, the value of $\lambda$ is -1
$\lambda \neq 1$ because in this case $\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$)
(ii)Solution:
The given equations are
$\lambda$x + y =$\lambda ^{2}$ , x + $\lambda$y = 1
In equation
$\lambda$x + y – $\lambda ^{2}$ = 0
a₁ = $\lambda$, b₁ = 1, c₁ = –$\lambda ^{2}$
In equation
x + $\lambda$y – 1 = 0
a₂ =1, b₂ = $\lambda$, c₂ = –1
$\frac{a_{1}}{a_{2}}=\frac{\lambda }{1}; \frac{b_{1}}{b_{2}}= \frac{1}{\lambda };\frac{c_{1}}{c_{2}}=\frac{-\lambda^{2} }{-1}= \lambda ^{2}$
For an infinite many solutions
$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
$\frac{\lambda }{1}= \frac{1}{\lambda }= \lambda ^{2}$
Only one value of l satisfies all three equations, that is $\lambda$ = 1
(iii) Solution:
The given equations are
$\lambda$x + y = $\lambda^{2}$, x + $\lambda$y = 1
In equation
$\lambda$x + y – $\lambda^{2}$ = 0
a₁ =$\lambda$ , b₁ = 1, c₁ = -$\lambda^{2}$
In equation
x + $\lambda$y = 1
a₂ =1, b₂ = $\lambda$, c₂ =–1
$\frac{a_{1}}{a_{2}}= \frac{\lambda }{1};\frac{b_{1}}{b_{2}}= \frac{1}{\lambda};\frac{c_{1}}{c_{2}}= \frac{-\lambda^{2} }{-1}= \lambda ^{2}$
For unique solution $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$
$\Rightarrow$$\frac{\lambda }{1}\neq \frac{1}{\lambda }$
$\Rightarrow$$\lambda ^{2}\neq 1$
$\Rightarrow$$\lambda \neq \pm 1$
All real values of $\lambda$ except $\lambda \neq \pm 1$

Question 2

For which value(s) of k will the pair of equations kx+ 3y = k – 3, 12x + ky= k have no solution?

Answer:

Solution:
The given equations are
kx + 3y = k –3
12x + ky = k
In equation
kx + 3y = k – 3
a₁ = k, b₁ = 3, c₁ = –k + 3
In equation
12x + ky = k
a₂ = 12, b₂ = k, c₂ = –k
$a_{2}= 12,b_{2}= k,c_{2}= -k$
$\frac{a_{1}}{a_{2}}= \frac{k}{12},\frac{b_{1}}{b_{2}}= \frac{3}{k},\frac{c_{1}}{c_{2}}= \frac{-k+3}{-k}= \frac{k-3}{k}$
We know that if the equations have no solution, then
$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
$\Rightarrow$$\frac{k}{12}= \frac{3}{k}\equiv \frac{k-3}{k}$
$\Rightarrow$$\frac{k}{12}= \frac{3}{k}$
$\Rightarrow$$k^{2}$ = 36
$\Rightarrow$$k= \pm 36$
($k\neq 6$ because if $k= +6$, then $\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$ which is not possible in no solution.)
Hence, the value of k is –6.

Question 3

For which values of a and b, will the following pair of linear equations have infinitely many Solutions?
x + 2y =1, (a – b)x+ (a + b)y = a + b – 2

Answer:

Solution:
The given equations are
x + 2y = 1
(a – b) x + (a + b)y = a + b – 2
In equation
x + 2y = 1
a₁ = 1, b₁ = 2, c₁ = –1
In equation
(a – b)x (a + b)y = a + b – 2
a₂ = (a – b), b₂ = (a + b), c₂ = – (a + b – 2)
$\frac{a_{1}}{a_{2}}= \frac{1}{\left ( a-b \right )},\frac{b_{1}}{b_{2}}= \frac{2}{\left ( a+b \right )},\frac{c_{1}}{c_{2}}= \frac{-1}{-\left ( a+b-2 \right )}$
For infinitely many Solutions $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
$\frac{1}{\left ( a-b \right )}= \frac{2}{\left ( a+b \right )}= \frac{1}{a+b-2 }$
$\Rightarrow$$\frac{1}{\left ( a-b \right )}= \frac{2}{\left ( a+b \right )}\; \;$
$\Rightarrow$a + b = 2a –2b
$\Rightarrow$–a + 3b = 0 … (1)

$\Rightarrow$$\frac{2}{\left ( a+b \right )}= \frac{1}{a+b-2}$
$\Rightarrow$2a + 2b – 4 = a + b
$\Rightarrow$ a + b –4 = 0 …(2)

Add equations (1) and (2)
$\Rightarrow$–a + 3b + a + b = 0 + 4
$\Rightarrow$4b = 4
b = 1
Put b = 1 in equation (1)
$\Rightarrow$–a + 3 (1) = 0
$\Rightarrow$a = 3
Hence, a = 3 and b = 1.

Question 4

Find the value(s) of p in for the following pair of equations:
(i) 3x – y – 5 = 0 and 6x – 2y – p = 0, if the lines represented by these equations are parallel.
(ii) – x + py = 1 and px – y = 1,if the pair of equations has no solution.
(iii) – 3x + 5y = 7 and 2px – 3y = 1,
if the lines represented by these equations are intersecting at a unique point.
(iv) 2x + 3y – 5 = 0 and px– 6y – 8 = 0,if the pair of equations has a unique solution.
(v) 2x + 3y = 7 and 2px + py = 28 – qy,if the pair of equations have infinitely many Solutions.

Answer:

(i)Solution:
In equation 3x – y – 5 = 0
a₁ = 3, b₁ = –1, c₁ = –5
In equation 6x – 2y – p = 0
a₂ = 6, b₂ = –2, c₂ = –p
$\frac{a_{1}}{a_{2}}= \frac{3}{6}= \frac{1}{2};\frac{b_{1}}{b_{2}}= \frac{-1}{-2}= \frac{1}{2};\frac{c_{1}}{c_{2}}= \frac{-5}{-p}= \frac{5}{p}$
If the lines are parallel $\frac{a_{1}}{a_{1}}= \frac{b_{1}}{b_{1}}\neq \frac{c_{1}}{c_{1}}$
$\Rightarrow$$\frac{1}{2}= \frac{1}{2}\neq \frac{5}{p}$
$\Rightarrow$$\frac{1}{2}\neq \frac{5}{p}\Rightarrow p\neq 10$
Any real value of p except 10.
(ii)Solution:
Here, the equations are
–x + py = 1, px – y = 1
In equation
–x + py = 1
a₁ = –1, b₁ = p, c₁ = –1
In equation
px – y = 1
a₂ = p, b₂ = –1, c₂ = –1
$\frac{a_{1}}{a_{2}}= \frac{-1}{p};\frac{b_{1}}{b_{2}}= \frac{p}{-1}= -p,\frac{c_{1}}{c_{2}}= \frac{-1}{1}= 1$
For no solution $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
$\Rightarrow$$\frac{-1}{p}= -p\neq 1$
$\Rightarrow$$\frac{+1}{p}= +p$
$\Rightarrow$$p^{2}$ = 1
$\Rightarrow$p = ± 1
$\Rightarrow$ p = + 1 ($p\neq -1$ because if p = –1 then $\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$)
(iii)Solution:
Here the equation are –3x + 5y = 7, 2px – 3y = 1
In equation –3x + 5y = 7
a₁ = –3, b₁ = 5, c₁ = –7
In equation 2px – 3y = 1
a₂ = 2p, b₂ = –3, c₂ = –1
$\frac{a_{1}}{a_{2}}= \frac{-3}{2p};\frac{b_{1}}{b_{2}}= \frac{5}{-3},\frac{c_{1}}{c_{2}}= \frac{-7}{-1}= 7$
For unique solution $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$
$\Rightarrow$$\frac{-3}{2p}\neq \frac{-5}{3}$
$\Rightarrow$$-9\neq -10p$
$\Rightarrow$$p\neq \frac{9}{10}$
$\Rightarrow$$p\neq 0\cdot 9$
Hence, p can have any real value for a unique solution except 0.9
(iv)Solution:
Here the equation are 2x + 3y – 5 = 0
px – 6y –8 = 0
In equation 2x + 3y – 5 = 0
a₁ = 2, b₁ = 3, c₁ = –5
In equation px – 6y – 8 = 0
a₂ = p, b₂ = –6, c₂ = –8
$\frac{a_{1}}{a_{2}}= \frac{2}{p};\frac{b_{1}}{b_{2}}= \frac{3}{-6}= \frac{-1}{2};\frac{c_{1}}{c_{2}}= \frac{-5}{-8}= \frac{5}{8}$
For unique solution $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$
$\Rightarrow$$\frac{2}{p}\neq \frac{-1}{2}$
$\Rightarrow$$4\neq -p$
$\Rightarrow$$p\neq -4$
Hence, the equations have a unique solution for every real value of p except –4. (v)Solution:
Here, the given equations are 2x + 3y = 7
a₁ = 2, b₁ = 3, c₁ = –7
In equation 2px + py = 28 – qy
2px + py + qy = 28
2px + y(p + q) = 28
a₂ = 2p, b₂ = p + q, c₂ = –28
$\frac{a_{1}}{a_{2}}= \frac{2}{2p}= \frac{1}{p};\frac{b_{1}}{b_{2}}= \frac{3}{p+q};\frac{c_{1}}{c_{2}}= \frac{-7}{-28}= \frac{1}{4}$
For infinite many solution $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
$\Rightarrow$$\frac{1}{p}= \frac{3}{p+q}= \frac{1}{4}$
$\Rightarrow$$\frac{1}{p}= \frac{1}{4}$
$\Rightarrow$4 = p
$\Rightarrow$p = 4
$\frac{3}{p+q}= \frac{1}{4}$
$\Rightarrow$p + q = 12
Put p =4
$\Rightarrow$q=12-4
$\Rightarrow$q=8
For infinitely many Solutions, p = 4, q = 8

Question 5

Two straight paths are represented by the equations x – 3y = 2 and –2x + 6y = 5. Check whether the paths cross each other or not

Answer:

Solution:
Equations are: x – 3y – 2 = 0
–2x + 6y – 5 = 0
Here a₁ = 1, b₁ = –3, c₁ = –2
a₂ = –2, b₂ = 6, c₂ = –5

$\frac{a_{1}}{a_{2}}= -\frac{1}{2},\frac{b_{1}}{b_{2}}= \frac{-3}{6}= -\frac{1}{2},\frac{c_{1}}{c_{2}}= \frac{-2}{-5}= \frac{2}{5}$
As we know that two lines cross each other when $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$ but here $\frac{a_{1}}{a_{2}}= \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$

Hence, the paths do not cross each other.

Question 6

Write a pair of linear equations which has the unique solution x = – 1, y = 3. How many such pairs can you write?

Answer:

Solution:
Let the equations be
a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0
Put x = –1 and y = 3 in the given equations.
–a₁ + 3b₁ + c₁ = 0 … (1)
–a₂ + 3b₂ + c₂ = 0 … (2)
Since for different values of a₁, b₂, c₁ and a₂, b₂, c₂, we have different Solutions.
Hence, infinitely many pairs have x = –1, y = 3 as the solution.

Question 7

If 2x + y = 23 and 4x – y = 19, find the values of 5y – 2x and $\frac{y}{x}-2$

Answer:

Solution:
Given equations are
2x + y = 23 … (1)
4x – y = 19 … (2)
Using the elimination method in equations (1) and (2), we get
2x + y = 23
4x – y = 19
$\Rightarrow$6x = 42
$\Rightarrow$ x = $\frac{42}{6}= 7$
Putting x = 7 in equation (1), we get
$\Rightarrow$2(7) + y = 23
$\Rightarrow$y = 23 – 14
$\Rightarrow$y = 9
Now 5y – 2x = 5(9) – 2 (7)
$\Rightarrow$ 45 – 14
$\Rightarrow$ 31
$\Rightarrow$$\frac{y}{x}- 2= \frac{9}{7}-2$
$\Rightarrow$$\frac{y-14}{7}= \frac{-5}{7}$

Question 8

Find the values of x and y in the following rectangle [see Fig. ].

Answer:

Solution:
We know that opposite sides of a rectangle are equal
3x + y = 7 … (1)
x + 3y = 13 … (2)
Find the value of x and y using the elimination method in equations (1) and (2)
9x + 3y = 21 {Multiply (1) by 3}
x + 3y = 13
-___-___-_______
$\Rightarrow$8x = 8
$\Rightarrow$ x = $\frac{8}{8}$ = 1
Put x = 1 in equation (1)
$\Rightarrow$3(1) + y = 7
$\Rightarrow$3 + y = 7
$\Rightarrow$y = 7 – 3
$\Rightarrow$ y = 4

Question 9

Solve the following pairs of equations:
(i) x+ y = 3.3 ;$\frac{0\cdot 6}{3x-2y}= -1,3x-2y\neq 0$
(ii)$\frac{x}{3}+\frac{y}{4}= 4$ , $\frac{5x}{6}-\frac{y}{8}= 4$
(iii)$4x+\frac{6}{y}= 15;6x-\frac{8}{y}= 14,y\neq 0$
(iv)$\frac{1}{2x}-\frac{1}{y}= -1;\frac{1}{x}+\frac{1}{2y}= 8,x,y\neq 0$
(v)43x + 67y = – 24 ; 67x + 43y = 24
(vi)$\frac{x}{a}+\frac{y}{b}= a+b;\frac{x}{a_{2}}+\frac{y}{b^{2}}= 2 \left ( a,b\neq 0 \right )$
(vii)$\frac{2xy}{xy}= \frac{2}{3};\frac{xy}{2x-y}= \frac{-3}{10};x+y\neq 0,2x-y\neq 0$

Answer:

(i)Solution:
Given equations are x + y = 3.3 … (1)
0.6 = 2y – 3x …(2)
Using the elimination method in equations (1) and (2), we get
2x + 2y = 6.6 [multiply equation (1) by 2]
–3x + 2y = 0.6
+ – –
$\Rightarrow$5x = 6
$\Rightarrow$ x = $\frac{6}{5}$ = 1.2
Putting x = 1.2 in (1), we get
$\Rightarrow$1.2 + y = 3.3
$\Rightarrow$y = 3.3 – 1.2
$\Rightarrow$y = 2.1
(ii) Solution:
Given equations are :
$\frac{x}{3}+\frac{y}{4}= 4$ ………(1)
$\frac{5x}{6}-\frac{y}{8}= 4$ ……….(2)
Multiply equation (1) by 12 and equation (2) by 24, and then add them.
We get
$\Rightarrow$4x + 3y + 20x -3y = 48 + 96
$\Rightarrow$24x = 144
$\Rightarrow$$x= \frac{144}{24}= 6$
$\Rightarrow$x = 6
Put x = 6 in equation (1), We have
$\Rightarrow$$\frac{6}{3}+\frac{y}{4}= 4$
$\Rightarrow$$2+\frac{y}{4}= 4$
$\Rightarrow$$\frac{y}{4}= 4-2$
$\Rightarrow$$\frac{y}{4}= 2$
$\Rightarrow$y = 8
(iii)Solution:
Equation are: $4 x+\frac{6}{y}=15 \\$… (1)
$6 x-\frac{8}{y}=14$… (2)
Multiply equation (1) by 6 and equation (2) by 4, and then subtract equation (2) from equation (1)
24x + $\frac{36}{y}$ = 90
24x – 32/y = 56
– + –
$\Rightarrow$$\frac{36}{y}+\frac{32}{y}= 34$
$\Rightarrow$$\frac{36+32}{y}= 34$
$\Rightarrow$68 = 34y
$\Rightarrow$ y = $\frac{68}{34}= 2$
$\Rightarrow$y = 2
Putting y = 2 in equation (1), we get
$\Rightarrow$4x = 15 – 3
$\Rightarrow$4x = 12
$\Rightarrow$ x = $\frac{12}{4}$ = 3
$\Rightarrow$x = 3
(iv)Solution:
Let $\frac{1}{x}$ = u and $\frac{1}{y}$ = v and put in the given equations
u/2 – v = – 1 … (1)
u + $\frac{v}{2}$ = 8 … (2)
Multiply equation (1) by 2 and subtract from equation (2), we get
$\Rightarrow$$\frac{v}{2}+2v= 8+2$
$\Rightarrow$v + 4v = 10 × 2
$\Rightarrow$5v = 20
$\Rightarrow$ v = $\frac{20}{+5}= 4$
$\Rightarrow$v = 4
$\Rightarrow$ v = $\frac 1y$ = 4
$\Rightarrow$ y = $\frac{1}{4}$
Putting v = 4 in equation (1), we get
$\Rightarrow$u/2= –1 + 4
$\Rightarrow$u = 6
$\Rightarrow$$\frac{1}{x} = 6$
(because $\frac 1x$ = u)
$\Rightarrow x= \frac{1}{6}$
(v)Solution:
Equations are 43x + 67y = –24 … (1)
67x + 43y = 24 … (2)
Multiply equation (1) by 67 and equation (2) by 43, and then subtract equation (2) from (1)
2881x + 4489y = –1608
2881x + 1849y = 1032
– – –
2640y = –2640
y = –1
Putting y = –1 in (1), we get
$\Rightarrow$43x + 67(–1) = –24
$\Rightarrow$43x = –24 + 67
$\Rightarrow$43x = 43
$\Rightarrow$x = 1
(vi)Solution:
Given equations are:
$\frac{x}{a}+\frac{y}{b}= a+b$

$\frac{x}{a^{2}}+\frac{y}{b^{2}}= 2$

$\frac{x}{a}+\frac{y}{b}-\left ( a+b \right )= 0$

$\frac{x}{a^{2}}+\frac{y}{b^{2}}-2= 0$
Using cross multiplication, we have

$\Rightarrow$$\frac{x}{\frac{-2}{b}+\frac{a}{b^{2}}+\frac{1}{b}}= \frac{-y}{\frac{-2}{a}+\frac{1}{a}+\frac{b}{b^{2}}}= \frac{1}{\frac{1}{ab^{2}}-\frac{1}{ba^{2}}}$
$\Rightarrow$$\frac{x}{\frac{a-b}{b^{2}}}= \frac{-y}{\frac{-a+b}{a^{2}}}= \frac{1}{\frac{1}{ab^{2}}-\frac{1}{b^{2}}}$
$\Rightarrow$$\frac{x}{\frac{a-b}{b^{2}}}=\frac{1}{\frac{+\left ( a-b \right )}{a^{2}b^{2}}}$
$\Rightarrow$$x= \frac{\left ( a-b \right )\times a^{2} b^{2}}{b^{2}\left ( a-b \right )}$
$\Rightarrow$ x = a²
$\Rightarrow$$\frac{-y}{\frac{-\left ( a-b \right )}{a^{2}}}= \frac{1}{\frac{\left ( a-b \right )}{a^{2}b^{2}}}$
$\Rightarrow$ y = $\frac{\left ( a-b \right )a^{2}b^{2}}{a^{2}\left ( a-b \right )}$
$\Rightarrow$ y = b²
(vii)Solution:
$\frac{2xy}{x+y}= \frac{3}{2}$ … (1)
$\frac{xy}{2x+y}= \frac{-3}{10}$… (2)
Inverse equations (1) & (2), then simplify them, we get
$\frac{x}{2xy}+\frac{y}{2xy}= \frac{2}{3}$
$\frac{1}{2y}+\frac{1}{2x}= \frac{2}{3}$ … (3)
$\frac{2x}{xy}-\frac{y}{xy}= \frac{-10}{3}$
$\frac{2}{y}-\frac{1}{x}= \frac{-10}{3}$…(4)
Divide equation (4) by 2, and we get
$\frac{2}{2y}-\frac{1}{2x}= \frac{-5}{3}$ … (5)
Adding (3) and (5), we get
$\Rightarrow$$\frac{2}{2y}+\frac{1}{2y}= \frac{-5}{3}+\frac{2}{3}$
$\Rightarrow$$\frac{2+1}{2y}= -\frac{5+2}{3}= \frac{-3}{3}= -1$
$\Rightarrow$2 + 1 = –2y
$\Rightarrow$ y = $-\frac{3}{2}$
Put y = $-\frac{3}{2}$ in equation (4) we have
$\Rightarrow$$\frac{4}{-3}-\frac{1}{x}= \frac{-10}{3}$
$\Rightarrow$$-\frac{10}{3}+\frac{4}{3}= \frac{-1}{x}$
$\Rightarrow$$-\frac{6}{3}= \frac{-1}{x}$
$\Rightarrow$$x= \frac{3}{6}= \frac{1}{2}$

Question 10

Find the solution of the pair of equation $\frac{x}{10}+\frac{y}{5}-1= 0$ and $\frac{x}{8}+\frac{y}{6}= 15$.
Hence, find $\lambda$, if y = $\lambda$x + 5.

Answer:

Solution:

$\frac{x}{10}+\frac{y}{5}= 1\Rightarrow \frac{x+2y}{10}= 1\Rightarrow$ x + 2y = 10 …(1)

$\frac{x}{8}+\frac{y}{6}= 15\Rightarrow \frac{3x+4y}{24}= 15\Rightarrow$ 3x + 4y = 360 … (2)
Multiply equation (1) by 2 and subtract from equation (2), we get
$\Rightarrow$3x – 2x = 360 – 20.
$\Rightarrow$x = 340
Putting x = 340 in equation 1, we get
$\Rightarrow$340 + 2y = 10
$\Rightarrow$2y = 10 – 340
$\Rightarrow$ y = $-\frac{330}{2}$
$\Rightarrow$y = – 165
$\Rightarrow$ y = $\lambda$x + 5
Put x = 340 and y = –165 we get
$\Rightarrow$ –165 = $\lambda$(340) + 5
$\Rightarrow$ –170 = $\lambda$(340)
$\Rightarrow$$\lambda = \frac{-1}{2}$

Question 11

By the graphical method, find whether the following pair of equations are consistent or not. If consistent, solve them. (i) 3x + y + 4 = 0 ; 6x– 2y + 4 = 0
(ii) x– 2y = 6 ; 3x – 6y = 0
(iii) x + y = 3 ; 3x + 3y = 9

Answer:

(i)Solution:
Given equations are 3x + y + 4 = 0
6x – 2y + 4 = 0
Here a₁ = 3, b₁ = 1, c₁ = 4
a₂ = 6, b₂ = –2, c₂ = 4
$\frac{a_{1}}{a_{2}}= \frac{3}{6}= \frac{1}{2},\frac{b_{1}}{b_{2}}= \frac{-1}{2},\frac{c_{1}}{c_{2}}= \frac{4}{4}= \frac{1}{1}$
$\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$
Hence, the given pair of linear equations are intersecting at one point.
Hence, given a pair of linear equations is consistent
Let us plot the graph of the given equations
In equation 3x + y + 4 = 0

In equation 6x – 2y + 4 = 0

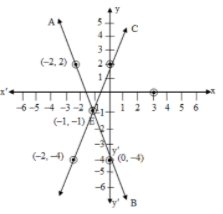
Here, two lines AB and CD intersect at only one point, that is E. Hence, the given pair of linear equations is consistent.(ii)Solution:
Given equations are x –2y –6 = 0
3x – 6y = 0
Here a₁ = 1, b₁ = –2, c₁ = –6
a₂ = 3, b₂ = –6, c₂ = 0
$\frac{a_{1}}{a_{2}}= \frac{1}{3},\frac{b_{1}}{b_{2}}= \frac{-2}{6}= \frac{1}{3},\frac{c_{1}}{c_{2}}= \frac{-6}{0}$
Here $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$
Here, the given pair of linear equations is parallel. Therefore, it has no solution. Hence, the given pair of linear equations is inconsistent
(iii)Solution:
The given equations are x + y – 3 = 0
3x +3y – 9 = 0
Here a₁ = 1, b₁ = 1, c₁ = –3
a₂ = 3, b₂ = 3, c₂ = –9
$\frac{a_{1}}{a_{2}}= \frac{1}{3},\frac{b_{1}}{b_{2}}= \frac{1}{3},\frac{c_{1}}{c_{2}}= \frac{-3}{-9}= \frac{1}{3}$
$\Rightarrow \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}}$
Therefore, the given pair of equations is coincident and has infinitely many solutions. Hence, the given pair of linear equations is consistent. Let us plot the graph of the given equations
x + y = 3

3x + 3y = 9

Here, lines AB and CD are coincident. Therefore, the above linear equations have infinitely many Solutions.

Question 12

Draw the graph of the pair of equations 2x + y = 4 and 2x – y = 4. Write the vertices of the triangle formed by these lines and the y-axis. Also find the area of this triangle.

Answer:

Solution:
Given equations are:
2x + y = 4
2x –y = 4
2x + y = 4

2x-y=4

Hence, from the above graph, it is clear that both the lines and the y-axis make triangle ABC.
Now, the area of triangle ABC is
$\Rightarrow$ 2(area of $\bigtriangleup$AOB)
$\Rightarrow$$2\left ( \frac{1}{2}\times OB\times OA\right )$

$\Rightarrow$$2\left ( \frac{1}{2}\times 2\times 4\right )$
$\Rightarrow$2(4)
$\Rightarrow$8 sq. units.
Hence, the required area of the triangle is 8 sq. units.

Question 13

Write an equation of a line passing through the point representing solution of the pair of linear equations x + y = 2 and 2x – y = 1. How many such lines can we find?

Answer:

Solution:
Given equations are x + y = 2
2x – y = 1
x + y = 2

2x – y = 1

From the graph, it is clear that two lines AB and CD intersect and point E (1, 1) Hence, infinite lines can pass through the intersecting point E, like 4 = x, 2x – y = 1, etc.

Question 14

If x + 1 is a factor of 2x³+ ax²+ 2bx + 1, then find the values of a and b given that 2a – 3b = 4.

Answer:

Solution:
It is given that (x + 1) is a factor of P(x) = 2x³ + ax² + 2bx + 1, then according to the remainder theorem, P(–1) is equal to 0.
$\Rightarrow$ P(–1) = 2(–1)³ + a(–1)² + 2b (–1) + 1
$\Rightarrow$0 = –2 + a – 2b + 1
$\Rightarrow$a – 2b = 1 … (1)
Given 2a – 3b = 4 … (2)
Solving equations (1) and (2) by the substitution method
2a – 4b = 2 {multiply equation (1) by 2}
2a – 3b = 4
– + –
$\Rightarrow$–b = –2
$\Rightarrow$b = 2
Put b = 2 in equation (1)
$\Rightarrow$a – 2(2) = 1
$\Rightarrow$a – 4 = 1
$\Rightarrow$a = 1 + 4
$\Rightarrow$ a = 5

Question 15

The angles of a triangle are x, y and $40^{\circ}$. The difference between the two angles x and y is $30^{\circ}$. Find x and y.

Answer:

Solution:
Given: x – y = $30^{\circ}$ …(1)

According to the sum of interior angles of a triangle property
x + y + $40^{\circ}$ = 180
x + y = $140^{\circ}$ … (2)
Solve equations (1) and (2) using the substitution method.
x – y = $30^{\circ}$
x + y = $140^{\circ}$
$\Rightarrow$2x = 170
$\Rightarrow$ x = $\frac{170}{2}$
$\Rightarrow$ x = $85^{\circ}$
Put x = $85^{\circ}$ in equation (1) We get
$\Rightarrow$$85^{\circ}$– y =$30^{\circ}$
$\Rightarrow$$85^{\circ}$ – $30^{\circ}$ = y
$\Rightarrow$$55^{\circ}$ = y

Question 16

Two years ago, Salim was thrice as old as his daughter and six years later, he will be four years older than twice her age. How old are they now?

Answer:

Solution: Let x be the age of Salim
y is the age of his daughter
According to the question
$\Rightarrow$(x – 2) = 3(y – 2)
$\Rightarrow$x – 2 = 3y – 6
$\Rightarrow$x – 3y = –4 …(1)
According to the second condition
$\Rightarrow$x + 6 = 2(y + 6) + 4
$\Rightarrow$x + 6 = 2y + 12 + 4
$\Rightarrow$x – 2y = 10 … (2)
Solve (1) and (2) by the substitution method
x – 3y = – 4
x – 2y = 10
– + –
$\Rightarrow$–y = – 14
$\Rightarrow$y = 14
Put y = 14 in equation (1)
$\Rightarrow$x – 3(14) = – 4
$\Rightarrow$x – 42 = –4
$\Rightarrow$x = –4 + 42
$\Rightarrow$x = 38
Salim’s age = 38 years
His daughter’s age = 14 years

Question 17

The age of the father is twice the sum of the ages of his two children. After 20years, his age will be equal to the sum of the ages of his children. Find the age of the father.

Answer:

Solution:
Let x be the age of the father, y and z be the ages of the children
According to the Question
x = 2 (y + z) … (1)
After 20 years
$\Rightarrow$x + 20 = (y + 20) + (z + 20)
$\Rightarrow$x + 20 = y + z + 40
$\Rightarrow$x + 20 – 40 = y + z
$\Rightarrow$x – 20 = y + z … (2)
Putting the value of (y + z) from equation (2) in equation (1), we get
$\Rightarrow$x = 2 (x – 20)
$\Rightarrow$x = 2x – 40
$\Rightarrow$x – 2x = – 40
$\Rightarrow$–x = – 40
$\Rightarrow$x = 40
Hence, the father’s age is 40 years

Question 18

Two numbers are in the ratio 5:6. If 8 is subtracted from each of the numbers, the ratio becomes 4:5. Find the numbers

Answer:

Solution:
Let x and y be two numbers
According to the question
x : y = 5 : 6
$\frac{x}{y}= \frac{5}{6}$
x = $\frac{5y}{6}$ … (1)
According to the second condition
$\frac{x-8}{y-8}= \frac{4}{5}$
5x – 40 = 4y – 32
5x – 4y = –32 + 40
5x – 4y = 8 … (2)
Putting the value of x from equation (1) in (2), we get
$\Rightarrow$$5\left ( \frac{5y}{6} \right )-4y= 8$
$\Rightarrow$$\frac{25y}{6}-4y= 8$
$\Rightarrow$$\frac{25y-24y}{6}= 8$
$\Rightarrow$25y – 24y = 48
$\Rightarrow$y = 48
Put y = 48 in equation (1)
$\Rightarrow$ x = $\frac{5\times 48}{6}$
$\Rightarrow$ x = 40

Question 19

There are some students in the two examination halls A and B. To make the number of students equal in each hall, 10 students are sent from A to B. But if 20 students are sent from B to A, the number of students in A becomes double the number of students in B. Find the number of students in the two halls.

Answer:

Solution:
According to the Question
Let x and y be the number of students in Class A and B.
x – 10 = y + 10
x – y = 20 … (1)
Second condition is
$\Rightarrow$(x + 20) = 2(y – 20)
$\Rightarrow$x + 20 = 2y – 40
$\Rightarrow$x – 2y = – 60 … (2)
Subtract (1) and (2), we get
$\Rightarrow$y = 20 + 60
$\Rightarrow$y = 80
Put y = 80 in (1)
$\Rightarrow$x – 80 = 20
$\Rightarrow$x = 20 + 80
$\Rightarrow$x = 100
Hence, in hall A, there are 100 students, and in hall B, there are 80 students.

Question 20

A shopkeeper gives books on rent for reading. She takes a fixed charge for the first two days, and an additional charge for each day thereafter. Latika paid Rs 22 for a book kept for six days, while Anand paid Rs 16 for the book kept for four days. Find the fixed charges and the charge for each extra day.

Answer:

Solution:
Let x be the fixed charges, and y be the extra charges for each day.
According to the question equation for Latika is
x + 4y = 22 … (1)
For Anand
x + 2y = 16 … (2)
Subtract equation (1) and (2), we get
$\Rightarrow$4y – 2y = 22 – 16
$\Rightarrow$2y = 6
$\Rightarrow$ y = $\frac{6}{2}$ = 3
Put y = 3 in equation (1)
$\Rightarrow$x + 4 (3) = 22
$\Rightarrow$x = 22 – 12
$\Rightarrow$x = 10
The fixed charge is = 10 Rs.
Additional charges = 3 Rs.

Question 21

In a competitive examination, one mark is awarded for each correct answer while $\frac{1}{2}$ mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly?

Answer:

Solution:
Let x be the number of correct answers and (120 – x) be the number of wrong answers.
According to the question
$\Rightarrow$ x – $\frac{\left ( 120-x \right )}{2}= 90$
$\Rightarrow$$\frac{2x-120+x}{2}= 90$
$\Rightarrow$3x – 120 = 180
$\Rightarrow$3x = 180 + 120
$\Rightarrow$3x = 300
$\Rightarrow$$x= \frac{300}{3}$
$\Rightarrow$x = 100
Hence, Jayanti answered 100 questions correctly.

Question 22

The angles of a cyclic quadrilateral ABCD are $\angle$A = (6x + 10)°, $\angle$B = (5x)° $\angle$C = (x + y)°, $\angle$D = (3y – 10)°
Find x and y, and Hence, the values of the four angles.

Answer:

Solution:
According to the property of a cyclic quadrilateral, the sum of opposite angles = $180^{\circ}$.
$\angle$A + $\angle$C = $180^{\circ}$
6x + $10^{\circ}$ + x + y = $180^{\circ}$
7x + y = $180^{\circ}$ –$10^{\circ}$
7x + y = $170^{\circ}$ … (1)
Similarly $\angle$B + $\angle$D = $180^{\circ}$
5x + 3y – $10^{\circ}$ = $180^{\circ}$
5x + 3y = $180^{\circ}$ + $10^{\circ}$
5x + 3y = $190^{\circ}$ … (2)
Solving equations (1) and (2), we get
21x + 3y = $510^{\circ}$ {Multiply equation (1) by 3} … (3)
Now subtract equation (2) from (3) then we get
$\Rightarrow$ 16x = $320^{\circ}$
$\Rightarrow$$x= \frac{320^{\circ}}{16}$
$\Rightarrow$ x = $20^{\circ}$
Put x = $20^{\circ}$ in equation (1) we get
$\Rightarrow$ 7($20^{\circ}$) + y = $170^{\circ}$
$\Rightarrow$ y = $170^{\circ}$ – $140^{\circ}$
$\Rightarrow$ y = $30^{\circ}$
Hence, $\angle$A = 6x + $10^{\circ}$
$\Rightarrow$ 6 × $20^{\circ}$ +$10^{\circ}$
$\Rightarrow$ $120^{\circ}$ + $10^{\circ}$
$\Rightarrow$ $130^{\circ}$
$\angle$B = (5x)
$\Rightarrow$ 5 × $20^{\circ}$ = $100^{\circ}$
$\angle$$c= \left ( x+y \right )^{\circ}$
$\Rightarrow$ ($20^{\circ}$ + $30^{\circ}$) = $50^{\circ}$
$\angle$D = (3y – 10)°
$\Rightarrow$ 3 × $30^{\circ}$ –$10^{\circ}$
$\Rightarrow$ $90^{\circ}$ –$10^{\circ}$
$\Rightarrow$ $80^{\circ}$
Hence, the value of four angles are:
$130^{\circ}$, $100^{\circ}$, $50^{\circ}$ and $80^{\circ}$ respectively.

Question 1

Graphically, solve the following pair of equations:2x + y = 6 and 2x – y + 2 = 0 Find the ratio of the areas of the two triangles formed by the lines representing these equations with the x-axis and the lines with the y-axis.

Answer:

Solution:
Here the equations are 2x + y = 6, 2x – y = –2
2x + y = 6

2x – y = –2

In the graph, we find that the lines intersect at (1, 4) Hence, x = 1, y = 4 is the solution of the equations.The two triangles are ABC and DBE
Area of $\bigtriangleup$ABE = $\frac{1}{2}$ × Base × perpendicular
$= \frac{1}{2}\times 4\times 4= 8$
Area of $\bigtriangleup$ADC = $\frac{1}{2}$ × Base × perpendicular
$= \frac{1}{2}\times 4\times 1$

$= 2$
$\bigtriangleup$ABE area : $\bigtriangleup$ADC Area = 4: 1

Question 2

Determine, graphically, the vertices of the triangle formed by the lines y = x, 3y = x, x + y = 8

Answer:

Solution:
y = x
y – x = 0

3y – x = 0

x + y = 8

The required triangle is $\bigtriangleup$ABC with vertices (0, 0), (4, 4), (2, 6).

Question 3

Draw the graphs of the equations x = 3, x = 5 and 2x – y – 4 = 0. Also find the area of the quadrilateral formed by the lines and the x–axis.

Answer:

Solution:
The given equations are x = 3, x = 5, 2x – y – 4 = 0
2x – y = 4

The quadrilateral ABCD is a trapezium.
Area of ABCD (trapezium) = $\frac{1}{2}$ × (a + b)h
a = AD, b = BC, h = AB
$\Rightarrow$ $\frac{1}{2}$× (AD + BC) × AB

$\Rightarrow$ $\frac{1}{2}$× (2 + 6) × 2

Area = 8 sq. units

Question 4

The cost of 4 pens and 4 pencil boxes is Rs 100. Three times the cost of a pen is Rs 15 more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and a pencil box.

Answer:

Solution:
Let the cost of a pen is x and the cost of a pencil box is y.
As per the question
4x + 4y = 100 … (1)
3x = y + 15 … (2)
Divide equation (1) by 4.
x + y = 25 ………..(3)
By adding equations (1) and (3) we get
$\Rightarrow$4x = 40
$\Rightarrow$x = 10
Put x = 10 in equation (1)
$\Rightarrow$40 + 4y = 100
$\Rightarrow$4y = 100 – 40
$\Rightarrow$y = 60/4 = 15
x = 10, y = 15
Cost of pen = Rs. 10
The cost of pencil box = Rs.15

Question 5

Determine, algebraically, the vertices of the triangle formed by the lines 3x – y = 3, 2x – 3y = 2 and x + 2y = 8

Answer:

Solution:
Determine, algebraically, the vertices of the triangle formed by the lines
3x – y = 3 … (1)
2x – 3y = 2 … (2)
x + 2y = 8 ... (3)

For vertices of A, solve equation (1) and (3)
3x – y = 3
x + 2y = 8 × 3
$\Rightarrow$3x + 6y = 24
$\Rightarrow$3x + y = –3
$\Rightarrow$7y = 21
$\Rightarrow$y = 3
Put y = 3 in equation (1)
$\Rightarrow$3x – 3 = 3
$\Rightarrow$3x = 6
$\Rightarrow$x = 2
point A is (2, 3)
For the vertices of B, solve equations (1) and (2)
3x – y = 3 × 3
2x – 3y = 2
9x – 3y = 9
– + –
–7x = –7
x = 1
Put x = 1 in equation (1)
$\Rightarrow$3(1) – y = 3
$\Rightarrow$3 – 3 = y
$\Rightarrow$y = 0
Point B is (1, 0)
For the vertices of C, solve (2) and (3)
2x – 3y = 2
x + 2y = 8 × 2
2x + 4y = 16
2x – 3y = 2
– + –
7y = 14
y = 2
Put y = 2 in equation (2)
$\Rightarrow$2x – 3(2) = 2
$\Rightarrow$2x = 2 + 6
$\Rightarrow$ x = $\frac{8}{2}$ = 4
Point C (4, 2)
Hence, vertices of triangle ABC are A (2, 3), B (1, 0), and C (4, 2)

Question 6

Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hour if she travels 2 km by rickshaw, and the remaining distance by bus.On the other hand, if she travels 4 km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.

Answer:

Solution:
We know that
Speed = $\frac{Distance}{Time}$
Time = Distance / Speed
Let the speed of the rickshaw be x and of the bus be y.
So, according to the question
$\frac{2}{x}+\frac{\left ( 14-2 \right )}{y}= \frac{1}{2}Hr$
$\frac{2}{x}+\frac{12}{y}= \frac{1}{2}\cdots (1)$
$\frac{4}{x}+\frac{10}{y}= \frac{39}{60}\, Hour\cdots (2)$
Solve equations (1) and (2)
$\left ( \frac{2}{x}+\frac{12}{y} = \frac{1}{2}\right )\times 2$
$\frac{4}{x}+\frac{24}{y}= 1$
$\frac{4}{x}+\frac{10}{y}= \frac{39}{60}$
2(1) - (2)
$\Rightarrow$$\frac{24}{y}-\frac{10}{y}=1- \frac{39}{60}$
$\Rightarrow$$\frac{24-10}{y}= \frac{60-39}{60}$
$\Rightarrow$$\frac{14}{y}= \frac{21}{60}$
$\Rightarrow$21y = 840
$y= \frac{840}{21}= 40$
Put y = 40 in equation (1)
$\Rightarrow$$\frac{2}{x}+\frac{12}{40}= \frac{1}{2}$
$\Rightarrow$$\frac{2}{x}= \frac{20-12}{40}$
$\Rightarrow$$\frac{2}{x}= \frac{8}{40}$
$\Rightarrow$40 = 4x
$\Rightarrow$x = 10
Speed of rickshaw = 10 km/h
Speed of bus = 40 km/h

Question 7

A person, rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream.

Answer:

Solution:
According to the question,
Person’s speed with upstream = (5 – x) km/h
Person’s speed with downstream = (5 + x) km/h
Time with upstream $= \frac{40}{5-x}\left ( Using\, t= \frac{D}{S} \right )$
Time with downstream $= \frac{40}{5+x}\left ( Using\, t= \frac{D}{S} \right )$
$\Rightarrow$$\frac{40}{5-x}= \frac{3\times 40}{5+x}$
$\Rightarrow$(5 + x)40 = 120 (5 – x)
$\Rightarrow$200 + 40x = 600 - 120 x
$\Rightarrow$160x = 400
$\Rightarrow$x = 2.5
Speed of stream = 2.5 km/h

Question 8

A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream.

Answer:

Solution:
Let speed of boat in still water = x km/h
Let speed of stream = y km/h
Speed of boat in upstream = (x - y) km/h
Speed of boat in downstream = (x + y) km/h
We know that time =$\frac{distance}{speed}$
So, $\frac{30}{\left ( x-y \right )}+\frac{28}{x+y}= 7$… (1)
$\frac{21}{\left ( x-y \right )}+\frac{21}{x+y}= 5$ … (2)
Put $\frac{1}{\left ( x-y \right )}= u,\frac{1}{\left ( x+y \right )}= v$ in (1), (2)
30u + 28v = 7 … (3)
21u + 21v = 5 … (4)
Solve equation (3), (4)
Multiply equation (3) by 21 and (4) by 30
630u + 588 v = 147
630u + 630v = 150
30(4) - 21(3)
+42v = +3
$v= \frac{3}{42}= \frac{1}{14}$
Put $v= \frac{1}{14}$ in equation (4)
$\Rightarrow$$21u+21\left ( \frac{1}{14} \right )= 5$
$\Rightarrow$$21u= 5-\frac{3}{2}$
$\Rightarrow$$21u= \frac{10-3}{2}$
$\Rightarrow$21u = $\frac{7}{2}$
$\Rightarrow$$u= \frac{7}{2\times 21}\Rightarrow u= \frac{1}{6}$
We put $u= \frac{1}{x-y}\, and\, v= \frac{1}{x+y}$
So,
$\frac{1}{x-y}= \frac{1}{6}$ | $\frac{1}{x+y}= \frac{1}{14}$
x-y=6..(5) x+y=14...(6)
By adding equations (5) and (6)
$\Rightarrow$2x = 20
$\Rightarrow$x = 10
Put x = 10 in equation (6)
$\Rightarrow$10 + y = 14
$\Rightarrow$y = 4
Hence, speed of the boat in still water = 10 km/hr.
Speed of the stream = 4 km/hr.

Question 9

A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number.

Answer:

Solution:
Let the first digit = x
Let the ten’s digit = y
Therefore the number = 10y + x
As per the question
8(x + y) –5 = 10y + x
8x + 8y – 10y – x = 5
7x – 2y = 5 … (1)
16(y – x) + 3 = 10y + x
16y – 16x – 10y – x = – 3
–17x + 6y = –3
17x – 6y = 3 … (2)
Multiply equation (1) by 3
21x – 6y = 15
17x – 6y = 3
3(1) + (2)
$\Rightarrow$4x = 12
$\Rightarrow$x = 3
Put x = 3 in equation (1)
$\Rightarrow$7(3) –2y = 5
$\Rightarrow$–2y = 5 –21
y = $\frac{16}{2}$ = 8
Hence, the number = 10y + x = 10(8) + 3 = 83

Question 10

A railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket. One reserved first Class ticket from the station A to B costs Rs 2530. Also, one reserved first Class ticket and one reserved first Class half ticket from A to B costs Rs 3810. Find the full first Class fare from station A to B, and also the reservation charges for a ticket.

Answer:

Solution:
Let the full ticket cost = y Rs.
Let reservation charge = x Rs.
According to questions
x + y = 2530 … (1)
(x + y) + (x + y/2) = 3810 …(2)
Here x + y is for full ticket and x + y/2 is for half.
Solve equation (1) and (2)
x + y + x + $\frac{y}{2}$ = 3810
2x + y + $\frac{y}{2}$ = 3810
4x + 2y + y = 3810 × 2
4x + 3y = 7620 … (3)
Multiply equation (1) by 3
3x + 3y = 7590
4x + 3y = 7620
3(1) - (3)
$\Rightarrow$–x = – 30
Put x = 30 in equation (1)
$\Rightarrow$30 + y = 2530
$\Rightarrow$y = 2500
Hence, Reservation charge = Rs. 30
Full first-Class charge = Rs. 2500

Question 11

A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, there by, getting a sum Rs 1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got Rs 1028. Find the cost price of the saree and the list price (price before discount) of the sweater.

Answer:

Solution:
Let the cost price of saree = Rs. x
Let the cost price of sweater = Rs. y
Saree with 8% profit = $(1+\frac{8}{100})x=\frac{108x}{100}$
Sweater with 10% discount = $(1-\frac{10}{100})y$ = $\frac{90y}{100}$
Saree with 10% profit = x + $x\times \frac{10}{100}= \frac{110x}{100}$
Sweater with 8% discount = y – $y\times \frac{8}{100}= \frac{92y}{100}$
According to Question
$\frac{108x}{100}+ \frac{92y}{100}= 1008$
108x + 90y = 100800
6x + 5y = 5600 … (1) (Divide by 18)
$\frac{110x}{100}+ \frac{92y}{100}= 1028$
110x + 92y = 102800
55x + 56y = 51400 … (2) (Divide by 2)
Multiply equation (1) by 46 and equation (2) by 5
276 x + 230 y = 257600
275 x + 230 y = 257000
46(1) – 5(2)
$\Rightarrow$x = 600
Put x = 600 in equation (1)
$\Rightarrow$6(600) + 5y = 5600
$\Rightarrow$5y = 5600 –3600
$\Rightarrow$5y = 2000
$\Rightarrow$y = 400
Price of saree = Rs. 600
Price of sweater = Rs. 400

Question 12

Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received Rs 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received Rs 20 more as annual interest. How much money did she invest in each scheme

Answer:

Solution:
Let money invested in A and B are x, y respectively.
So, according to question.
0.08x + 0.09y = 1860 … (1)

$x\times \frac{9}{100}+y\times \frac{8}{100}= 1880$
0.09x + 0.08y = 1880 … (2)
Multiply equation (1) by 9 and (2) by 8
0.72x + 0.81y = 16740
0.72x + 0.64y = 15040
9(1) - 8(2)
$\Rightarrow$ 0.17y = 1700

y = $\frac{1700}{0\cdot 7}= 10000$
Put y = 10000 in equation (1)
$\Rightarrow$0.08x + 900 = 1860
$\Rightarrow$0.08x = 960
$\Rightarrow$ x = $\frac{960}{8}\times 100$ = 12000
$\Rightarrow$x = 12000
He invested Rs. 12000 in A and Rs. 10000 in B.

Question 13

Vijay had some bananas, and he divided them into two lots A and B. He sold the first lot at the rate of Rs 2 for 3 bananas and the second lot at the rate of Re 1 per banana, and got a total of Rs 400. If he had sold the first lot at the rate of Re 1 per banana, and the second lot at the rate of Rs 4 for 5 bananas, his total collection would have been Rs 460. Find the total number of bananas he had.

Answer:

Solution:
Let bananas in lot A = x
Bananas in lot B = y
According to Question
$\left ( \frac{x}{3} \right )\left ( 2 \right )+y\left ( 1 \right )= 400$
2x + 3y = 400 × 3
2x + 3y = 1200 … (1)
x(1) + $\left ( \frac{y}{5} \right )$(4) = 460
5x + 4y = 460 × 5
5x + 4y = 2300 … (2)
Multiply equation (1) by 5 and equation (2) by 2
10x + 15y = 6000
10x + 8y = 4600
5(1) - 2(2)
$\Rightarrow$7y = 1400
$\Rightarrow$$y= \frac{1400}{7}= 200$
Put y = 200 in equation (1)
$\Rightarrow$2x + 3(200) = 1200
$\Rightarrow$2x + 600 = 1200
$\Rightarrow$2x = 600
$\Rightarrow$x = 300
Total number of bananas = x + y = 300 + 200 = 500