Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Exemplar Class 10 Maths Solutions Chapter 1 Real Numbers

NCERT Exemplar Class 10 Maths Solutions Chapter 1 Real Numbers

Edited By Ravindra Pindel | Updated on Sep 05, 2022 12:09 PM IST | #CBSE Class 10th

NCERT exemplar Class 10 Maths solutions chapter 1 is very important for all students who want to pursue mathematics in higher classes. This chapter provides a detailed understanding of real numbers. NCERT exemplar Class 10 Maths chapter 1 solutions can help the students build a strong base which will provide an extra edge while solving questions of NCERT Class 10 Maths.

This Story also Contains
  1. NCERT Exemplar Solutions Class 10 Maths Chapter 1 Important Topics:
  2. NCERT Class 10 Exemplar Solutions for Other Subjects:
  3. NCERT Class 10 Maths Exemplar Solutions for Other Chapters:
  4. Features of NCERT Exemplar Class 10 Maths Solutions Chapter 1:

These Class 10 Maths NCERT exemplar chapter 1 solutions are complete and descriptive which makes the learning of concepts of real numbers extremely effective. CBSE Syllabus for Class 10 has been kept in vision while preparing the NCERT exemplar Class 10 Maths solutions chapter 1.

Question:1

Choose the correct answer from the given four options in the following questions For some integer m, every even integer is of the form
(A) m
(B) m + 1
(C) 2m
(D) 2m + 1

Answer:

If the value of m is odd number than option A give odd number. Therefore, option A is not the answer of given question. When value of m is even, then option B always given odd number.
For example let m = 2, then m + 1 = 2 + 1 = 3
Which is odd hence B is not the answer.
When value of m is odd/even then option C gives always even number.
For example let m = 2, then 2 m = 4;
let m = 3, then 2 m = 6
Hence C is correct option.
Option D always gives odd integer for every value of m, hence option D is not the answer.

Question:2

For some integer q, every odd integer is of the form
(A) q
(B) q + 1
(C) 2q
(d) 2q + 1

Answer:

If the value of q is even number than option A gives even number. Therefore, option A is not the answer of given question.
When value of q is odd, then option B always gives even number.
For example let q = 3, then q + 1 = 3 + 1 = 4
Which is even hence B is not the answer.
When value of q is odd/even then option C gives always even number.
For example let m = 2, then 2 m = 4;
let m = 3, then 2 m = 6
Hence C is incorrect option.
Option D always gives odd integer for every value of q, hence option D is the answer.
For example let q = 2, then 2q + 1 = 2 × 2 + 1 \Rightarrow 5

Question:3

n2 – 1 divisible by 8, if n is
(A) an integer
(B) a natural number
(C) an odd integer
(D) an even integer

Answer:

let n = 2 then n2 – 1 = 4 – 1 = 3, which is not divisible by 8
When n is a natural number,
let n = 4 then n2 – 1 = 16 – 1 = 15, which is not divisible by 8
When n is an odd integer then n2 – 1 is always divisible by 8,
let n = 3, n2 – 1 = 9 – 1 = 8 which is divisible by 8.
Proof: let n = 2q + 1
n2– 1 = (2q + 1)2 – 1
= 4q2 + 1 + 4q – 1
= 4q (q + 1)
Product of two consecutive number is divisible by 2, hence number n2 – 1 is divisible by 8.
When n is an even integer then n2 – 1 is not divisible by 8.
let n = 2,
n2 – 1 = 4 – 1 = 3

Question:4

If the HCF of 65 and 117 is expressible in the form 65 m – 117, then the value of m is
(A) 4 (B) 2 (C) 1 (D) 3

Answer:

Answer. [B]
Solution. First of all let us find the HCF of 65 and 117
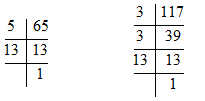
FireShot%20Capture%20069%20-%20Careers360%20CMS%20-%20cms-article%20-%20learn 65 = 1 × 5 × 13 117 = 1 × 3 × 13 × 3
HCF = 13 ….(1)
According to question HCF = 65 m – 117
Using (1)
13 = 65 m – 117
13 + 117 = 65 m
\frac{130}{65}= m
m = 2
Therefore, option (b) is correct.

Question:5

The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is
(A) 13 (B) 65 (C) 875 (D) 1750

Answer:

Answer. [A]
Solution. First of all subtract remainder from the given number.
(70 – 5) = 65
(125 – 8) = 117
Require number is HCF of 65 and 117
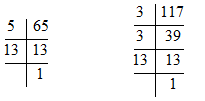
1617453871540 65 = 5 × 13 × 1
117 = 3 × 3 × 13 × 1
HCF = 13
Hence 13 is the largest number which is divides by 70 and 120 & leaves remainder 5 and 8.
Therefore, option (A) is correct.

Question:6

If two positive integers a and b are written as a = x3 y2 and b = xy3; x, y are prime numbers then HCF (a, b)
(A) xy (B) xy2 (C) x3y3 (D) x2y2

Answer:

a= x^{3}y^{2}\Rightarrow x\times x\times x\times y\times y
b= xy^{3}\Rightarrow x\times y\times y\times y
For HCF, we have to take all common prime numbers from both the numbers.
Hence,
\text{HCF = }x\times y\times y= xy^{2}
\text{ HCF =}xy^{2}
Hence option B is correct.

Question:7

If two positive integers p and q can be expressed as p = ab2 and q = a3b; a, b being prime numbers then LCM (p, q) is
(A) ab (B) a2b2 (C) a3b2 (D) a3b3

Answer:

Answer. [C]
Solution.
p= ab^{2}= a\times b\times b
q= a^{3}b= a\times a\times a\times b
For LCM, we have to take all the primes from prime factorization of two number.
The common prime in both numbers has to be taken only once.
Therefore,
\text{LCM =}a\times a\times a\times b\times b= a^{3}b^{2}
Hence option C is correct.

Question:8

The product of a non-zero rational and an irrational number is
(A) always irrational
(B) always rational
(C) Rational or irrational
(D) one

Answer:

Rational number is the number, which can be written:
in the form of p/q where q not equal to zero. (Here P and Q has to be an integer)
Irrational numbers cannot be written in the form of p/q.
Consider a rational number = 1/2
\text{ Irrational number =} \sqrt{3}
\text{Product =}\frac{1}{2}\times \sqrt{3}= \frac{\sqrt{3}}{2} \text{(irrational)}
Therefore, option (A) is correct.

Question:9

The least number that is divisible by all the numbers from 1 to 10 is:
(A) 10 (B) 504 (C) 100 (D) 2520

Answer:

Option A is not the answer of the question, because 10 is not divisible by 3, 4, 6, 7, 8, 9
Option B is also not the answer of the question, because 504 is not divisible by 5 and 10
Option (C) is also not the answer of the question because 100 is not divisible by 3, 6, 7, 8 and 9
Option (D) is the answer of the question because 2520 is divisible by all the numbers from 1 to 10.
Calculation:
Prime factorization of all the numbers:
1 = 1
2 = 2
3 =3
4 =2\times2
5 =5
6 = 3\times2
7 = 7
8 = 2\times2\times2
+9 = 3\times3
10 = 2\times5
For LCM, we have to take all the primes from prime factorization of two number.
The common prime in both numbers has to be taken only once.
Therefore,
LCM = 2\times2\times2\times3\times3\times3\times5\times7 =2520
Therefore, option (D) is correct.

Question:10

The decimal expansion of the rational numbers \frac{14587}{1250} will terminate after:
(A) one decimal place
(B) two decimal places
(C) there decimal places
(D) four decimal places

Answer:

Answer. [D]

\text{Rational number =}\frac{14587}{1250}
FireShot%20Capture%20072%20-%20Careers360%20CMS%20-%20cms-article%20-%20learn \Rightarrow \frac{14587}{2^{1}\times \left ( 5 \right )^{4}}

= \frac{14587}{2^{1}\times 5^{1}\times 5^{3}}
= \frac{14587}{10\times 5^{3}}\times \frac{2^{3}}{2^{3}} \text{{Divide and multiply by 23}}
= \frac{116696}{10000}= 11.6696
Hence the given rational number will terminate after four decimal places. (D) four decimal places

Question:1

Write whether every positive integer can be of the form 4q + 2, where q is an integer. Justify your answer

Answer:

The above statement is not true in all the conditions. For example, if we take the value of q as – 1. Then 4q + 2 = – 4 + 2 = – 2 which is not a positive integer.
And moreover, if q is positive then 4q + 2 will be always even. Therefore, we can never write an odd positive number in this form. Hence given statement is false

Question:2

The product of two consecutive positive integer is divisible by 2”. Is this statement true or false”? Justify your answer.

Answer:

The above statement is true in all the conditions. Consider a number P = q (q + 1)
If q is odd then q+ 1 will be even, hence P will be divisible by 2.
If q is even then q+ 1 will be odd, but P will be divisible by 2.
For example:
let us take numbers 2 and 3:
product is 2 x 3 = 6 which is divisible by 2
Hence given statement is true

Question:3

The product of three consecutive positive integers is divisible by 6”. Is this statement true or false? Justify your answer

Answer:

The given statement is true in all the conditions.
Let three consecutive positive integers be, x, x + 1 and x + 2.
Divisibility by 3: Whenever a number is divided by 3, the remainder obtained is either 0 or 1 or 2.
\thereforen = 3p or 3p + 1 or 3p + 2, where p is some integer.
So, we can say that one of the numbers among x, x + 1 and x + 2 is always divisible by 3.
\Rightarrow x (x + 1) (x + 2) is divisible by 3.
Divisibility by 2: Whenever a number is divided 2, the remainder obtained is 0 or 1.
\thereforen = 2q or 2q + 1, where q is some integer.
So, we can say that one of the numbers among x, x + 1 and x + 2 is always divisible by 2.
\Rightarrowx (x + 1) (x + 2) is divisible by 2.
Since, x (x + 1) (x + 2) is divisible by 2 and 3.
\therefore x (x + 1) (x + 2) is divisible by 6.

Question:4

Write whether the square of any positive integer can be of the form 3m + 2, where m is a natural number. Justify your answer

Answer:

Any positive integer can be written in the form of 3q or 3q+1 or 3q + 2.
Since square of 3q = 9q² = 3(3q²) = 3m (where 3q² = m)
Square of (3q+1) = (3q+1) ² = 9q²+1+6q = 3(3q²+2q) +1 = 3m + 1
(where, m = 3q² + 2q)
Square of (3q+2) = (3q+2) ² = 9q²+4+12q = 3(3q²+4q) +4 = 3m + 4 (where, m = 3q²+2q)

Thus, there is not any square of a positive integer, which can be written in the form of 3m + 2
Hence the given statement is false.

Question:5

A positive integer is of the form 3q + 1, being a natural number. Can you write its square in any form other than 3m + 1, i.e. 3m or 3m + 2 for some integer m? Justify your answer

Answer:

Let us take the square of (3q + 1)
(3q + 1)2 = (3q) 2 + (1)2 + 2 × 3q × 1
= 9q2 + 1 + 6q
= 9q2 + 6q + 1
= 3(3q2 + 2q) + 1
= 3m + 1
{where m = 3q2 + 2q}
Hence, the square of 3q + 1 (where q is a positive integer) cannot be
written in any form other than 3m + 1
Hence the given statement is false.

Question:6

The number 525 and 3000 are both divisible only by 3. 5, 15, 25 and 75 what is HCF (525, 3000)? Justify your answer.

Answer:

The highest common divisor of any two numbers is called HCF.
Here 75 is the highest common divisor.
We can also find HCF:
Applying Euclid’s division algorithm on 525 and 3000 we get
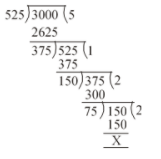
FireShot%20Capture%20075%20-%20Careers360%20CMS%20-%20cms-article%20-%20learn Hence 75 is the HCF of numbers 525 and 3000

Question:7

Explain why 3 \times 5 \times 7 + 7 is a composite number

Answer:

Composite number – the number which is divisible by a number other than one and itself. Here, 3 x 5 x 7 + 7 = 112 and 112 is divisible by 2, 4, 7, 8, 14, 16, 28 and 56. Hence it is a composite number.

Question:8

Can two numbers have 18 as their HCF and 380 as then LCM? Give reasons.

Answer:

As we know, LCM is a multiple of HCF
\frac{LCM}{HCF}has to be an integer.
If the given statement is true:
380 = 18n where n is any integer.
But there is no such type of n exist as we can say that 380 is not divisible by 18.
Hence two numbers, with 18 as their HCF and 380 as their LCM, do not exist.

Question:9

Without actually performing the long division, find if 987/10500 will have terminating or non-terminating decimal expansion give reason for your answer.

Answer:

We can also write this number as
:\frac{987}{10500}= \frac{3\times 7\times 47}{3\times 7\times 2^{2}\times 5^{3}}= \frac{47}{2^{2}\times 5^{3}}

= \frac{47}{2^{2}\times 5^{3}}\times \frac{2}{2}= \frac{47\times 2}{5^{3}\times 2^{3}}
= \frac{94}{\left ( 10 \right )^{3}}= \frac{94}{1000}= 0\cdot 094
Here, we have a finite number of digits after the decimal point.
Hence it is terminating decimal expansion.

Question:10

A rational number in its decimal expansion is 327.7081. What can you say about the prime factors of q, when this number is expressed in the formp/q? Give reason.

Answer:

The given decimal number is 327.7881.
327\cdot 7081= \frac{3277081}{10000}= \frac{p}{q}
The q is 10000, therefore its prime factorization, can be written as:
q = 10000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5
= 24 × 54 = (2 × 5)4

Question:1

Show that the square of any positive integer is either of the form 4q or 4q + 1 for some integer q

Answer:

Any positive integer can be written in the form of 4m or 4m + 1 or 4m + 2 or 4m + 3.
Case 1:
A = 4m
(4m)2 = 16 m2
=4(4m2)
=4q (Here q = 4m2)
Case 2:
A = 4m + 1
(4m + 1)2= (4m)2 + 1 + 8m
=16m2 + 8m + 1
=4(4m2 + 2m) + 1
=4q + 1 (here q = 4m2 + 2m)
Case 3:
A = 4m + 2
(4m + 2) 2
= 16 m2 + 4 + 16 m
=4 × (4m2 + 1) + 4 m
= 4q
Here q = (4m2 + 1 + 4m)
Case 4:
A = 4m + 3
(4m + 3)2 = 16 m2 + 9 + 24 m
4(4m2 + 6m + 2) + 1
4q + 1
here q = (4m2 + 6m +2)
Hence square of any positive integer is either of the form 4q or 4q + 1.

Question:2

Show that cube of any positive integer is of the form 4m, 4m + 1 or 4m + 3, for some integer m.

Answer:

By Euclid’s division –
Any positive integer can be written as:
A = bq + r
Here b = 4
r is remainder when we divide A by 4, therefore:
0\leq\ r <4 r = 0, 1, 2, 3
A = 4q + r …(1)
Case 1:
A = 4q
A3 = (4q)3 = 64q3 = 4(16q3)
A3 = 4m
(m = 16 q3)
Case 2:
A = 4q + 1
(4q + 1)3 = (4q)3 + (1)3 + 3(4q)2 (1) + 3(4q) (1)2
(Using (a + b)3 = a3+ b3 + 3a2b + 3ab2)
= 64q3 + 1 + 48q2 + 12q
= 4(16q3 + 12q2 + 3q) + 1
A3 = 4m + 1
(m = 16q3 + 12q2 + 3q)
Case 3:
A = 4q + 2
= (4q + 2)3 = (4q)3 + (2)3 + 3(4q)2 (2) + 3(4q) (2)2
(using (a + b)3 = a3 + b3 + 3a2b + 3ab2)
= 64q3 + 8 + 96q2 + 48q
= 4(16q3 + 2 + 24q2+ 12q)
= 4m
(m = 16q3 + 2 + 24q2 + 12 q)
Case 4:
A = 4q + 3
A3 = (4q + 3)2 = (4q)3 + (3)3 + 3(4q)2 (3) + 3(4q) (3)2
(Using (a + b)3 = a3 + b3 + 3a2b + 3ab2)
= 64q3 + 27 + 144q2 + 108q
= 64q3 + 24 + 144 q2 + 108q + 3
= 4(16q3 + 6 + 36q2 + 27q) + 3
= 4m + 3
(m = 16q3 + 6 + 36q2 + 27q)
Hence any positive integer’s cube can be written in the form of
4m, 4m + 1, 4m + 3.

Question:3

Show that the square of any positive integer cannot be of the form 5q + 2 or 5q + 3 for any integer q.

Answer:

By Euclid’s division –
Any positive integer can be written as:
A = bm + r
Here b = 5
r is remainder when we divide A by 5, therefore:
0 \leq r < 5, r = 0, 1, 2, 3.4
A = 5m + r …(1)
Case 1:
A = 5m
(5m)2 = 25 m2
= 5(5m2)
= 5q
(Here q = 5 m2)
Case 2:
A = 5m + 1
(5m + 1)2 = 25 m2 + 1 + 10 m
25m2 + 10 m + 1
5(5m2 + 2m) + 1
5q + 1
(Here q = 5m2 + 2m)
Similarly, we can verify it for 5m + 2, 5m + 3, 5m + 4
Here, square of any positive integer is in the form of 5q, 5q + 1
Hence, square of any positive integer cannot be of the form 5q + 2 or 5q + 3.

Question:4

Show that the square of any positive integer cannot be of the form 6m + 2 or 6m + 5 for any integer m

Answer:

By Euclid’s division –
Any positive integer can be written as:
A = bq + r
Here b = 6
r is remainder when we divide A by 5, therefore:
0 \leq r < 6, r = 0, 1, 2, 3,4,5
A = 6q + r …(1)
Case 1:
A = 6q
A2 = (6q)2 = 36q2 = 6(6q2)
A2 = 6m
(m = 6q2)
Case 2:
A = 6q + 1
A2 = (6q + 1)2
A2 = 36q2 + 1 + 2(6q)
(Using (a + b)2 = a2 + b2 + 2ab)
A2 = 36q2 + 1 + 12q
A2 = 6(6q2 + 2q) + 1
A2 = 6m + 1
(m = 6q2 + 2q)
Similarly, we can verify it for 6q + 2, 6q + 3, 6q + 4, 6q + 5
Now, it is clear that the square of any positive integer cannot be of the form 6m + 2, 6m + 5.

Question:5

Show that the square of any odd integer is of the form 4q + 1 for some integer q.

Answer:

By Euclid’s division –
Any positive integer can be written as:
A = bq + r
Here b = 4
r is remainder when we divide A by 4, therefore:
0 \leq r < 4, r = 0, 1, 2, 3
Even: A = 4q and 4q + 2
Odd: A = 4q + 1 and 4q + 3
Case 1:
Now squaring the odd terms, we get
(4q + 1)2 = (4q) 2 + (1)2 + 8q
= 16q2 + 8q + 1
= 4(4q2 + 2q) + 1
= 4m + 1
Here m = 4q2 + 2q
Case 2:
(4q + 3)2 = (4q)2 + (3)2 +24q
= 16q2 + 8 + 1 + 24q
=16q2 + 24q + 8 + 1
=4(4q2 + 6q + 2) + 1
=4m + 1
Here m = 4q2 + 6q + 2
Hence we can say that square of any odd integer is of the form 4q + 1 for some integer q.

Question:6

If n is an odd integer, then show that n2 – 1 is divisible by 8.

Answer:

We can represent any odd positive integer in the form of (4q + 1) or (4q + 3) for some integer q.
Case 1:
If n = 4q + 1
n2 – 1 = (4q + 1)2 –1
n2– 1 = (4q)2 + (1)2 + 2(4q) (1) – 1
Using (a + b)2 = a2 + b2 + 2ab
n2 – 1 = 16q2 + 1 + 8q – 1
n2 – 1 = 16q2 + 8q = 8q (2q + 1)
Which is divisible by 8.
Case 2:
If n = 4q + 3
n2 – 1 = (4q + 3)2 – 1
n2 – 1 = (4q)2 + (3)2 + 2(4q) (3) – 1
(Using (a + b)2 = a2 + b2 + 2ab)
n2 – 1 =16q2 + 9 + 24q –1
n2 – 1 = 16q2 + 8 + 24q = 8(2q2 + 1+3q)
Which is divisible by 8
Hence any odd positive integer n when written in n2 – 1 from is divisible by 8.

Question:7

Prove that if x and y are both odd positive integers, then x2 + y2 is even but not divisible by 4.

Answer:

We can represent any positive integer in the form of (2q +1) for any integer q.
Let x = 2q + 1; y = 2p + 1
x2 + y2 = (2q + 1)2 + (2p + 1)2
x2 + y2 = (2q)2 + (1)2 + 2(2q) (1) + (2p)2 + (1)2 + 2(2p) (1)
(Using (a + b) 2 = a2 + b + 2ab)
x2 + y2 = 4q2 + 1 + 4q + 4p2 + 1 + 4p
x2 + y2 = 2(2q2 + 2q + 2p2 + 2p + 1)
(2q2 + 2q + 2p2 + 2p + 1) is odd
Hence, x2 + y2 is divisible by 2 but not divisible by 4.

Question:8

Use Euclid’s division algorithm to find the HCF of 441, 567, 693

Answer:

First, we find the HCF of 441 and 567 by using Euclid division algorithm.
FireShot%20Capture%20078%20-%20Careers360%20CMS%20-%20cms-article%20-%20learn Here HCF of (567, 41) = 63 Now, we will find the HCF of 63 and 693

1617454186545

693 = 63 \times11 + 0
Therefore HCF of (63, 693) = 63
Thus HCF of (441, 467, 693) = 63.

Question:9

Using Euclid is division algorithm, find the largest number that divides 1251, 9377 and 15628 leaving remainders 1, 2 and 3 respectively.

Answer:

As we know that 1, 2 and 3 are the remainders of given number 1251, 9377 and 15628
After subtracting remainders, we get
1251 – 1 = 1250
9377 – 2 = 9375
15628 – 3 = 15625
Now HCF of 1250, 9375, 15625 can be calculated as:
First, we will calculate the HCF of 9375 and 15625;
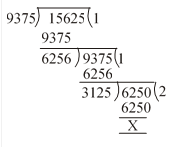
FireShot%20Capture%20081%20-%20Careers360%20CMS%20-%20cms-article%20-%20learn HCF (15625, 9375) = 3125 Now we will calculate the HCF of 3125 and 1250.
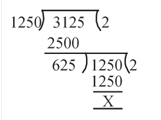
FireShot%20Capture%20084%20-%20Careers360%20CMS%20-%20cms-article%20-%20learn HCF of 3125 and 1250 is 625. Here HCF of (1250, 9375, 15625) = 625
Hence largest number is 625.

Question:10

Prove that \sqrt{3}+\sqrt{5} is irrational.

Answer:

We will do it by the method of contradiction: We will assume \sqrt{3}+\sqrt{5} is a rational number. If it leads to some absurd outcome then it is a wrong assumption.
Let \sqrt{3}+\sqrt{5} is a rational number
\therefore \sqrt{3}+\sqrt{5}= \frac{a}{b},b\neq 0,a,b\, \epsilon z
\sqrt{5}= \frac{a}{b}-\sqrt{3}
Squaring both side.
\left ( \sqrt{5} \right )^{2}= \left ( \frac{a}{b} -\sqrt{3}\right )^{2}
5= \left ( \frac{a}{b} \right )^{2}+\left ( \sqrt{3} \right )^{2}-2\left ( \frac{a}{b} \right )\left ( \sqrt{3} \right )
(Using (a – b)2 = a2 + b2 = 2ab)
\left ( \frac{a}{b} \right )^{2}+3-2\left ( \frac{a}{b} \right )\left ( \sqrt{3} \right )= 5
\frac{a^{2}}{b^{2}}+3-5= 2\sqrt{3}\left ( \frac{a}{b} \right )
\frac{a^{2}-2b^{2}}{b^{2}}= 2\sqrt{3}\left ( \frac{a}{b} \right )
\frac{b\left ( a^{2} -2b^{2}\right )}{2ab^{2}}= \sqrt{3}
\frac{a^{2}-2b^{2}}{2ab}= \sqrt{3}
LHS is a rational number but RHS is an irrational number.
This is not possible, hence our assumption was wrong.
Hence \sqrt{3}+\sqrt{5} is a irrational number.

Question:11

Show that 12n cannot end with the digit 0 or 5 for any natural number n.

Answer:

We know that, if any number ends up with digit 0 or 5 then it must be divisible by 5.
Here 12n = (2 × 2 × 3)n
12n = (22 × 3)n
12n = (22n × 3n)
5 is not there, in the prime factorization form.
Hence 12n can’t end with the digit 0 or 5.

Question:12

On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 45 cm, respectively. What is the minimum distance each should walk so that each can covers the same distance in complete steps?

Answer:

Step-length of first person = 40 cm
Step-length of second person = 42 cm
Step-length of third person = 45 cm
For finding minimum distance which will be multiple of all step-lengths. we have to find the LCM of (40, 42, 45)
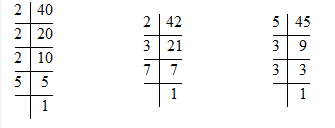
FireShot%20Capture%20087%20-%20Careers360%20CMS%20-%20cms-article%20-%20learn Prime factorization forms: 40 = 2 × 2 × 2 × 5 × 1
42 = 2 × 3 × 7 × 1
45 = 5 × 3 × 3 × 1
LCM = 2 × 3 × 5 × 2 × 2 × 7 × 3 = 2520
Hence minimum distance is 2520 cm.

Question:13

Write the denominator of the rational number 257/5000 in the form 2m × 5n, where m, n are non-negative integers. Hence, write its decimal expansion, without actual division.

Answer:

Here, denominator = 5000
It can be written as:
5000 = 2 × 2 × 2 × 5 × 5 × 5 × 5
Hence the given fraction \frac{257}{2^{3}\times 5^{4}} can be written as:
\Rightarrow \frac{257}{\left ( 2^{3}\times 5^{4} \right )5^{1}}
\Rightarrow \frac{257}{1000\times 5^{1}}\times \frac{2^{1}}{2^{1}} (On dividing & multiply by 21)
\Rightarrow \frac{514}{10000}
\Rightarrow 0\cdot 0514
Hence, it is a terminating decimal.

Question:14

Prove that \sqrt{p}+\sqrt{q} is irrational, where p, q are primes.

Answer:

We will do it by method of contradiction: We will assume \sqrt{p}+\sqrt{q} is a rational number. If it leads to some absurd outcome then it is wrong assumption.
Let \sqrt{p}+\sqrt{q} is a rational number
\sqrt{p}+\sqrt{q}= \frac{a}{b},b\neq a,a,b\epsilon z
\sqrt{q}= \frac{a}{b}-\sqrt{p}
Squaring both sides
\left ( \sqrt{q} \right )^{2}=\left ( \frac{a}{b}-\sqrt{p} \right )^{2}
q= \left ( \frac{a}{b} \right )^{2}+\left ( \sqrt{p} \right )^{2}-2\left ( \frac{a}{b} \right )\left ( \sqrt{p} \right )
(Using (a – b)2 = a2 + b2 – 2ab)
\frac{a^{2}}{b^{2}}+p-q= 2\sqrt{p}\frac{a}{b}
2\sqrt{p}\frac{a}{b}= \frac{a^{2}}{b^{2}}+p-q
\sqrt{p}= \frac{b\left ( a^{2}+b^{2}\left ( p-q \right ) \right )}{2ab^{2}}
\sqrt{p}= \frac{a^{2}+b^{2}\left ( p-q \right )}{2ab}
RHS is a rational number but LHS is an irrational number.
This is not possible, hence our assumption was wrong.
Here \sqrt{p}+\sqrt{q} has to be irrational.

Question:1

Show that the cube of a positive integer of the form 6q + r, q is an integer and r = 0, 1, 2, 3, 4, 5 is also of the form 6m + r.

Answer:

By Euclid’s division –
Any positive integer can be written as:
A = bq + r
Here b = 6
r is remainder when we divide A by 5, therefore:
0 \leq r < 6, r = 0, 1, 2, 3,4,5
A = 6q + r
Here A = 6q + r
A3 = (6q + r)3 = 216q3 + r3 + 3.6q.r (6q + r)
[\because (a + b)3 = a3 + b3 + 3ab (a + b)]
A3 = (216q3 + 108q2r + 18qr2) + r3 …(1)
Put r = 0, 1, 2, 3, 4, 5
Case 1:
A = 6q
A2 = 216q3
A3 =6 (36q3)
=6 (m )
Case 2:
A = 6q + 1
A3 = (216q3 + 108q2 + 18q) + 1
=6(36q3 + 18q2 + 3q) + 1
a3 = 6m + 1
{m = 36q3 + 18q2 + 3q}
Case 3:
A = 6q + 2
A3 = (216q3 + 216q3 + 72q) + 8
= (216q3 + 216q2 + 72q + 6) + 2
= 6m + 2
Case 4:
A = 6q + 3
A3=216q3 + 324q2 + 162q + 24 + 3
=6(36q3 + 54q2 + 27q + 4) + 3
= 6m + 3
{m = 36 q3 + 54q2 + 27q + 4}
Case 5:
A = 6q + 4
A3 = (216 q3 + 432 q2 + 288q) + 64
=6(36q3 + 72q2 + 48 q) + 60 + 4
=6(36q3 + 72q2 + 48q + 10) + 4
=6m + 4
{m = 36q3 + 72q2 + 48q + 10}
Case 6:
A = 6q + 5
A3 = (216 q3 + 540 q2 + 450 q) + 125
= 216 q3 + 540 q2 + 450 q + 120 + 5
= 6 (36q3 + 90q2 + 75 q + 20) + 5
= 6m + 5
(where m = 36 q3 + 90q2 + 75q + 20)
Hence, cube of a positive integer of the form 6q + r, q is a integer can be express in the form 6m + r where r = 0, 1, 2, 3, 4 and 5.

Question:2

Prove that one and only one out of n, n + 2 and n + 4 is divisible by 3, where n is any positive integer.

Answer:

Any positive integer can be written in form of 3m, 3m + 1 or 3m + 2
Case-1:
n = 3m
3m is divisible by 3
Adding two on both sides
n + 2 = 3m + 2
Here when n + 2 is divided by 3 it leaves remainder 2
Adding four on both sides
n + 4 = 3m + 4
= 3m + 3 + 1
= 3(m + 1) + 1
Here on dividing by 3, it leaves remainder 1
In this case n is divisible by 3 but (n + 2) and (n + 4) are not divisible by 3
Case-2 :
n = 3m + 1
on dividing by 3, it leaves remainder 1
adding two on both sides
n + 2 = 3m + 1 + 2
n + 2 = 3m + 3
= 3(m + 1)
on dividing by 3 it leaves remainder 0
Hence it is divisible by 3
adding four on both sides
x + 4 = 3m + 1 + 4
x + 4 = 3m + 3 + 2
= 3(m + 1) + 2
on dividing by 3, it leaves remainder 2
In this (n + 2) is divisible by 3 but n and (n + 4) are not divisible by 3
Hence through both the cases we conclude that one and only one out of n, n + 2 and n + 4 is divisible by 3, where n is any positive integer.
Similarly, we can show for n = 3m + 2 form.

Question:3

Prove that one of any three consecutive positive integers must be divisible by 3.

Answer:

Let three consecutive integers are n, n + 1, n + 2 when n is a natural number
i.e., n = 1, 2, 3, 4, ….
for n = 1, chosen numbers :(1, 2, 3) and 3 is divisible by 3
for n = 2, chosen numbers :(2, 3,4) and 3 is divisible by 3
for n = 3, chosen numbers :( 3, 4, 5) and 3 is divisible by 3
for n = 4, chosen numbers :(4, 5, 6) and 6 is divisible by 3
for n = 5, (chosen numbers :(5, 6, 7) and 6 is divisible by 3
Proof:
Case 1 : Let n is divisible by 3, it means n can be written as :
n = 3m,
Now, n +1 = 3m + 1 ; it gives remainder 1, when divided by 3
Now, n +2 = 3m + 2; it gives remainder 2, when divided by 3

Case 2: Let n + 1 is divisible by 3, it means n +1 can be written as :
n +1 = 3m,
Now, n = 3m – 1= 3(m – 1) + 2 ; it gives remainder 2, when divided by 3
Now, n +2 = 3m + 1; it gives remainder 1, when divided by 3
Case 3: Let n + 2 is divisible by 3, it means n +2 can be written as :
n +2 = 3m,
Now, n = 3m – 2= 3(m – 1) + 1 ; it gives remainder 1, when divided by 3
Now, n +1 = 3m – 1=3(m – 1) + 2 ; it gives remainder 2, when divided by 3

Question:4

For any positive integer n, prove that n3 – n is divisible by 6.

Answer:

Let three consecutive positive integers be, x, x + 1 and x + 2.
Divisibility by 3: Whenever a number is divided by 3, the remainder obtained is either 0 or 1 or 2
.\thereforen = 3p or 3p + 1 or 3p + 2, where p is some integer.
So, we can say that one of the numbers among x, x + 1 and x + 2 is always divisible by 3.
\Rightarrow x (x + 1) (x + 2) is divisible by 3.

Divisibility by 2: Whenever a number is divided 2, the remainder obtained is 0 or 1.
\therefore n = 2q or 2q + 1, where q is some integer.
So, we can say that one of the numbers among x, x + 1 and x + 2 is always divisible by 2.\Rightarrow
x (x + 1) (x + 2) is divisible by 2.
Since, x (x + 1) (x + 2) is divisible by 2 and 3.
\thereforex (x + 1) (x + 2) is divisible by 6.
Now the given number is:
P = n3 – n
P = n (n2 – 1)
P = n (n – 1) (n + 1)
P = (n – 1) n (n + 1)
Therefore, P is the product of three consecutive numbers.
Now P can be written as:
P = x (x + 1) (x + 2) which is is divisible by 6.
Hence P is divisible by 6.
Hence proved

Question:5

Show that one and only one out of n, n + 4, n + 8, n + 12 and n + 16 is divisible by 5, where n is any positive integer.

Answer:

By Euclid’s division –
Any positive integer can be written as:
n = bm + r
Here b = 5
r is remainder when we divide n by 5, therefore:
0 \leq r < 5, r = 0, 1, 2, 3.4
n = 5m + r, therefore n can have values:
n = 5m, 5m + 1, 5m + 2, 5m + 3, 5m + 4.
Here m is natural number
Case 1 : Let n is divisible by 5, it means n can be written as :
n = 5m,
Now, n +4 = 5m + 4;it gives remainder 4, when divided by 5
Now, n + 8 = 5m + 8= 5(m +1) +3; it gives remainder 3, when divided by 5
Now, n + 12 = 5m + 12= 5(m +2) +2; it gives remainder 2, when divided by 5
Now, n + 16 = 5m + 16= 5(m +3) +1; it gives remainder 1, when divided by 5
Case 2: Let n + 4 is divisible by 5, it means n + 4 can be written as :
n + 4 = 5m,
Now, n = 5m – 4 = 5(m – 1) + 1 ; it gives remainder 1, when divided by 5
Now, n + 8 = 5m + 4; it gives remainder 4, when divided by 5
Now, n + 12 = 5m + 8 = 5(m +1) +3; it gives remainder 3, when divided by 5
Now, n + 16 = 5m + 12 = 5(m +2) +2; it gives remainder 2, when divided by 5
Similarly, we can show for other cases.

NCERT Exemplar Solutions Class 10 Maths Chapter 1 Important Topics:

  • In this chapter, the students will learn to write any specific type of number in terms of variables; such as the representation of even number, odd number et cetera.
  • We will discuss a rational number and rational number and their properties.
  • In this chapter, we will use the remainder theorem to prove many other theorems
  • NCERT exemplar Class 10 Maths solutions chapter 1 explains the fundamental theorem of arithmetic.
  • In this chapter, students will learn about Euclid’s division lemma method.

NCERT Class 10 Exemplar Solutions for Other Subjects:

VMC VIQ Scholarship Test

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Apply
Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 15th NOV'24! Trusted by 3,500+ universities globally

Apply

NCERT Class 10 Maths Exemplar Solutions for Other Chapters:

Chapter 2 Polynomials

Chapter 3 Pair of Linear Equations in Two Variables

Chapter 4 Quadratic Equations

Chapter 5 Arithmetic Progressions

Chapter 6 Triangles

Chapter 7 Coordinate Geometry

Chapter 8 Introduction to Trigonometry & Its Equations

Chapter 9 Circles

Chapter 10 Constructions

Chapter 11 Areas related to Circles

Chapter 12 Surface Areas and Volumes

Chapter 13 Statistics and Probability

Features of NCERT Exemplar Class 10 Maths Solutions Chapter 1:

  • These Class 10 Maths NCERT exemplar chapter 1 solutions provide a basic knowledge of real numbers which has great importance in higher classes.

  • The questions based on Real Numbers can be practiced in a better way along with these solutions.

  • The NCERT exemplar Class 10 Maths chapter 1 solution Real Numbers has a good amount of problems for practice and are sufficient for a student to easily sail through other books such as NCERT Class 10 Maths, RD Sharma Class 10 Maths, RS Aggarwal Class 10 Maths.

NCERT exemplar Class 10 Maths solutions chapter 1 pdf download are available through online tools for the students to access this content in an offline version so that no breaks in continuity are faced while practicing NCERT exemplar Class 10 Maths chapter 1.

Check Chapter-Wise Solutions of Book Questions

Must, Read NCERT Solution Subject Wise

Check NCERT Notes Subject Wise

Also, Check NCERT Books and NCERT Syllabus here

Frequently Asked Questions (FAQs)

1. What is the divisibility test by three?

 If the sum of digits is divisible by three then the number will be divisible by three.

2. Is the chapter Real Numbers important for competitive examinations like JEE Advanced?

The chapter on Real Numbers is important for competitive examinations like JEE Advanced. A better understanding of the concepts will help the student solve complex problems in higher classes and competitive examinations.

3. What is the mark distribution of Real Numbers in the final boards examination?

The chapter on Real Numbers holds around 7-9% of the total marks of the paper. NCERT exemplar Class 10 Maths solutions chapter 1 can help the students learn the concepts and provide ample amount of practice questions.

4. Is the chapter Real Numbers important for Board examinations?

The chapter of Real Numbers is extremely important for Board examinations as it holds around 7-8% weightage of the whole paper.

Also Read

Articles

Upcoming School Exams

Himachal Pradesh Board of Secondary Education 12th Examination

Application Date:09 September,2024 - 14 November,2024

Himachal Pradesh Board of Secondary Education 10th Examination

Application Date:09 September,2024 - 14 November,2024

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

National Means Cum-Merit Scholarship

Application Date:05 October,2024 - 04 November,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 812 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
IBM
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 15th NOV'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST
CBSE conducts surprise inspections at 27 schools in Rajasthan, Delhi to curb menace of dummy schools
September 03, 2024 - 03:02 PM IST
CBSE Class 10 compartment result 2024 declared; 48.83% pass
August 05, 2024 - 03:14 PM IST
CBSE Class 10 compartment result 2024 soon; passing marks, websites to check
August 05, 2024 - 02:44 PM IST
CBSE Class 10 compartment result 2024 expected soon at cbseresults.nic.in; grading system, passing marks
August 04, 2024 - 04:20 PM IST

Stay up-to date with CBSE Class 10th News

Back to top