NCERT Exemplar Class 10 Maths solutions Chapter 9 Circles

NCERT Exemplar Class 10 Maths Solutions Chapter 9 Circles

Question 1: If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is (A) 3 cm (B) 6 cm (C) 9 cm (D) 1 cm

Answer:

According to the question,

Here, A is the center, AB = 4 cm radius of a small circle, and AD = 5 cm radius of a large circle.

We have to find the length of the CD

$\Delta$ABD is a right-angle triangle.

Hence, use Pythagoras' theorem in $\Delta$ABD

$\left ( AD \right )^{2}= \left ( AB \right )^{2}+\left ( BD \right )^{2}$

$\left ( 5 \right )^{2}= \left ( 4 \right )^{2}+\left ( BD \right )^{2}$

$25-16= \left ( BD \right )^{2}$

$BD= \sqrt{9}= 3$

$BD= 3cm$

$CD= CB+BD$

$CD= CB+BD$

$CD= BD+BD= 2BD\; \; \left ( \because CB= BD \right )$

$CD= 2\times 3= 6cm$

$CD= 6cm$

Hence, the length of the chord is 6 cm.

Hence, the answer is option (B).

Question:2 In Figure, if ∠AOB = 125°, then ∠COD is equal to (A) 62.5° (B) 45° (C) 35° (D) 55°

Answer:

Given : ∠AOB = 125°

Let ∠COD = x°

As we know, the sum of opposite sides' angles of a quadrilateral circumscribing a circle is equal to 180°.

Hence

∠AOB + ∠COD = 180°

125° + ∠COD = 180°

x° = 180° – 125° ($\mathbb{Q}$ ∠COD = x°)

x° = 55°

Hence, ∠COD = 55°

Hence, the answer is option (D).

Question:3 In Figure, AB is a chord of the circle, and AOC is its diameter such that $<$ ACB = 50°. If AT is tangent to the circle at point A, then $\angle$ BAT is equal to (A) 65° (B) 60° (C) 50° (D) 40°

Given $\angle$ ACB = 50°.

We know that the angle subtended by a diameter is right.

Hence $\angle$B = 90°

We know that the sum of the interior angles of a triangle is 180°.

In $\bigtriangleup$ABC

$\angle A+\angle B+\angle C= 180^{\circ}$

$\angle A+90^{\circ}+50^{\circ}= 180^{\circ}$

$\angle A=180^{\circ}-140^{\circ}$

$\angle A= 40^{\circ}$

That is $\angle CAB= 40^{\circ}$

$\angle CAT= \angle CAB+\angle BAT$

$90^{\circ}= 40^{\circ}+\angle BAT$ $\left (\because CA \perp AT \right )$

$\angle BAT= 90^{\circ}-40^{\circ}$

$\angle BAT= 50^{\circ}$

Question:4 From a point P which is at a distance of 13 cm from the center O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is (A) 60 cm^2 (B) 65 cm^2 (C) 30 cm^2 (D) 32.5 cm^2

Answer:

According to the question

Given OP = 13 cm

OQ = OR = radius = 5 cm

In $\bigtriangleup$POQ, $\angle Q= 90^{\circ}$ ($\because$ PQ is tangent)

Using Pythagoras' theorem in $\bigtriangleup$POQ

$\left ( PO \right )^{2}= \left ( PQ \right )^{2}+\left ( QO \right )^{2}$ ( because H² = B² + P²)

$\left ( 13 \right )^{2}= \left ( PQ \right )^{2}+\left ( 5 \right )^{2}$

$\left ( PQ\right )^{2}= 169-25$

$PQ= \sqrt{144}= 12$

$PQ= 12$

Area of $\bigtriangleup$POQ = $\frac{1}{2}$ × perpendicular × base

$= \frac{1}{2}\times PQ\times OQ$

$= \frac{1}{2}\times 12\times 5= 30cm^{2}$

Area of quadrilateral = 2 × area of $\bigtriangleup$POQ

= 2 × 30 = 60 cm²

Question:5 At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance of 8 cm from A is (A) 4 cm (B) 5 cm (C) 6 cm (D) 8 cm

Answer:

According to questions

Given AO = OB = 5 cm

Distance between XY and CD = 8 cm

Since D is the center of the circle and CD is a chord. If we join OD, it becomes the radius of the circle that is OD = 5cm

AZ = 8 cm (given)

AZ = AO + OZ

8 = 5 + OZ

OZ = 3cm

In $\bigtriangleup$ODZ, use Pythagoras theorem

$\left ( OD \right )^{2}= \left ( OZ \right )^{2}+\left ( ZD \right )^{2}$

$\left ( 5 \right )^{2}= \left ( 3 \right )^{2}+\left ( ZD \right )^{2}$

$\left ( ZD \right )^{2}= 25-9$

$ZD= \sqrt{16}= 4cm$

$CD= CZ+ZD$

$CD= ZD+ZD$ $\left ( \because CZ= ZD \right )$

$CD= 2ZD= 2\left ( 4 \right )= 8cm$

Length of chord CD = 8 cm

Question:6 In Figure, AT is tangent to the circle with center O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to (A) 4 cm (B) 2 cm (C) $2\sqrt{3}cm$ (D) $4\sqrt{3}cm$

(A) 4 cm (B) 2 cm (C) $2\sqrt{3}cm$ (D) $4\sqrt{3}cm$

Answer:

Given ∠OTA = 30° , OT = 4cm

Join OA, since AT is tangent.

Hence, it is perpendicular to OA

In $\bigtriangleup$OAT

$\cos \theta = \frac{B}{H}$

$\cos 30^{\circ} = \frac{AT}{OT}$

$\frac{\sqrt{3}}{2}= \frac{AT}{4}\; \; \left ( \because \cos 30^{\circ}= \frac{\sqrt{3}}{2} \right )$

$AT= 4\times \frac{\sqrt{3}}{2}$

$AT= 2\sqrt{3}cm$

Question:7 In Figure, if O is the center of a circle, PQ is a chord, and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to (A) 100° (B) 80° (C) 90° (D) 75°

Answer:

Given :$\angle QPR= 50^{\circ}$

We know that the tangent is perpendicular to the radius.

Hence $PR\perp PO$

$\angle$OPR = $90^{\circ}$

$\angle$OPR = $\angle$OPQ + $\angle$QPR

$90^{\circ}$ = $\angle$ OPQ + $50^{\circ}$

$\angle$OPQ = $40^{\circ}$

$\angle$OPQ = $\angle$OQD $\left ( \because \, OP= OQ \, radius\, of\, circle\right )$

Hence , $\angle$OPQ = $40^{\circ}$

We know that the sum of the interior angles of a triangle is $180^{\circ}$

In $\bigtriangleup OPQ$

$\angle$O+$\angle$Q +$\angle$P = $180^{\circ}$

$\angle$O +40+40 = 180

$\angle$o = $100^{\circ}$

Hence $\angle$OPQ = $100^{\circ}$

Question:8 In Figure, if PA and PB are tangents to the circle with center O such that $\angle$APB = 50°, then $\angle$OAB is equal to (A) 25° (B) 30° (C) 40° (D) 50°

Answer:

Given : $\angle$APB = 50°

We know that the length of tangents drawn from an external point is equal

Hence, PA = PB

Since, PA = PB

Let $\angle$PAB = $\angle$ PBA = x⁰

In $\bigtriangleup$PAB

$\angle$p+$\angle$A+$\angle$B = $180^{\circ}$($\because$ Sum of interior angles of a tangent is $180^{\circ}$)

$50^{\circ}+x^{\circ}+x^{\circ}= 180^{\circ}$

$2x^{\circ}= 130^{\circ}$

$x^{\circ}= 65^{\circ}$

$\angle$PAB = $\angle$PBA = $65^{\circ}$

$\angle$PAO = $90^{\circ}$ ($\mathbb{Q}$ tangent is perpendicular to radius)

$\angle$PAO = $\angle$PAB +$\angle$OAB

$90^{\circ}= 65^{\circ}+\angle OAB$

$\angle OAB= 90^{\circ}-65^{\circ}$

$\angle OAB= 25^{\circ}$

Question:9 If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm, then the length of each tangent is equal to (A) $\frac{3}{2}\sqrt{3}cm$ (B) 6 cm (C) 3 cm (D) $3\sqrt{3}cm$

Answer:

According to the question

Given OQ = OR = 3 cm (Radius)

$\angle P= 60^{\circ}$

Draw a line OP which bisects $\angle P$. That is $\angle OPQ= 30^{\circ}$

$\angle OPR= 30^{\circ}$

In $\bigtriangleup OPQ$

$\tan \theta = \frac{P}{B}$

$\tan 30^{\circ} = \frac{3}{PQ}$

$\frac{1}{\sqrt{3}}= \frac{3}{PQ}$

$PQ= 3\sqrt{3}$

Here PQ = PR

Hence , PQ = PR= $3\sqrt{3}$

Question:10

In the Figure, if PQR is tangent to a circle at Q whose center is O, AB is a chord parallel to PR, and$\angle$ BQR = 70°, then $\angle$ AQB is equal to

A) 20° (B) 40° (C) 35° (D) 45°

Answer:

Given :$\angle BQR= 70^{\circ}$, $AB\parallel PR$

Since DQ is perpendicular to PR

$\angle DQR= 90^{\circ}$

$\angle DQR= \angle DQB+\angle BQR$

$90^{\circ}= \angle DQB+70^{\circ}$

$\angle DQB= 20^{\circ}$

Since DQ bisect $\angle AQB$

Hence , $\angle DQB=\angle DQA= 20^{\circ}$

$\angle AQB= \angle DQB+\angle DQA$

$= 20^{\circ}+20^{\circ}= 40^{\circ}$

$\angle AQB= 40^{\circ}$

Question:1

Write ‘True’ or ‘False’ and justify your answer in each of the following :
If a chord AB subtends an angle of $60^{\circ}$ at the center of a circle, then the angle between the tangents at A and B is also $60^{\circ}$.

Answer:

Here, CA and CB are the two tangents that are drawn on chord AB, and we also know that tangents and radius are perpendicular to each other.

i.e.,$\angle CBO=\angle CAO= 90^{\circ}$

In quadrilateral, ABCD

$\angle A+\angle B+\angle C+\angle O= 360^{\circ}$

[$\mathbb{Q}$ Sum of interior angles of a quadrilateral is $360^{\circ}$]

$90^{\circ}+90^{\circ}+\angle C+60^{\circ}= 360^{\circ}$

$\angle C= 360^{\circ}-60^{\circ}-90^{\circ}-90^{\circ}$

$\angle C= 120^{\circ}$

Here, we conclude that the angle between the tangents at A and B is $120^{\circ}$.

Therefore, the given statement is False.

Question:2

Write ‘True’ or ‘False’ and justify your answer in each of the following: The length of the tangent from an external point on a circle is always greater than the radius of the circle.

Answer:

Case I – When the external point P is very close to the circle

Here, C is the center of the circle. Let this radius be 5 and the distance of Px and Py be 3. Or we can say that Case I contradicts the given statement.

Case II – When the external point P is far from the circle.

Here the radius of the given circle is 5 cm, and let the length of Px and Py be 10 cm.

Hence, according to Case II, the given statement is True.

Hence, from the above two cases, we conclude that the tangent’s length is dependent on the distance of an external point from the circle.

Therefore given statement is False because the length of a tangent from an external point of a circle may or may not be greater than the radius of the circle.

Therefore, the given statement is False.

Question:3

Write ‘True’ or ‘False’ and justify your answer in each of the following: The length of the tangent from an external point P on a circle with center O is always less than OP.

Answer:

Here, O is the center of the given circle, and PA is the tangent, which is drawn from an external point P. OA is the radius of the circle. We know that the tangent and radius are always perpendicular to each other.

$\therefore \, \angle A= 90^{\circ}$

$\therefore$ $\bigtriangleup PAO$ is a right angle triangle Use Pythagoras theorem in $\bigtriangleup PAO$

$\left ( PO \right )^{2}= \left ( OA \right )^{2}+\left ( PA \right )^{2}$ …..(i)

From equation (I), we can say that PA is always less than PO.

In other words, we can say that the length of the hypotenuse is always greater than the length of the perpendicular in a right-angle triangle.

i.e., OP $>$ PA

Hence, the given statement is True.

Question:4

Write ‘True’ or ‘False’ and justify your answer in each of the following: The angle between two tangents to a circle may be $0^{\circ}$.

Answer:

The angles of two lines may be $0^{\circ}$ in only two conditions.

1. When lines are parallel

2. When both the lines coincide.

Hence, the given statement is True.

This may be possible only when tangents are parallel or when both tangents coincide.

Hence, the given statement is true.

Question:5

Write ‘True’ or ‘False’ and justify your answer in each of the following: If the angle between two tangents drawn from a point P to a circle of radius a and center O is $90^{\circ}$, then $OP= a\sqrt{2}$

Answer:

Given $\angle APB= 90^{\circ}$

Draw a line OP from point O to P, which bisects $\angle P$.

i.e , $\angle OPB= 45^{\circ}$

In $\bigtriangleup OBP$

$\sin 45= \frac{OB}{OP}$

$\therefore \sin \theta = \frac{perpendicular}{hypotenuse}$

$\frac{1}{\sqrt{2}}= \frac{a}{OP}$

$OP= a\sqrt{2}$

Hence, the given statement is True.

Question:6

Write ‘True’ or ‘False’ and justify your answer in each of the following: If the angle between two tangents drawn from a point P to a circle of radius a and center O is $60^{\circ}$, then $OP= a\sqrt{3}$

Answer:

Given $\angle APB= 60^{\circ}$

Draw a line OP from point O to P, which bisects P. Which bisect $\angle P$

i.e, $\angle APO= 30^{\circ}$

In $\bigtriangleup OAP$

$\sin 30^{\circ}= \frac{OA}{OP}$

$\therefore \sin \theta = \frac{perpendicular}{hypotenuse}$

$\frac{1}{2}= \frac{a}{OP}$

OP = 2a

Hence, the value of OP = 2a

Hence, the given statement is False.

Question:7

Write ‘True’ or ‘False’ and justify your answer in each of the following: The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.

Answer:

Given ABC is an isosceles triangle and AB = AC.

To Prove : $XY\parallel BC$

Proof : AB = AC (Given)

$\angle ABC= \angle ACB$

[The angle between the chord of a circle and the tangent is equal to the angle made by the chord in an alternate segment]

Also $\angle XAB= \angle ABC$

$\Rightarrow \angle XAB= \angle BCA$

$\Rightarrow XAY\parallel BC$

i.e , $\Rightarrow XY\parallel BC$

Hence, the given statement is true.

Question:8

Write ‘True’ or ‘False’ and justify your answer in each of the following
If several circles touch a given line segment PQ at point A, then their centers lie on the perpendicular bisector of PQ.

Answer:

According to the question.

Here C₁, C₂, C₃ are the circle with center O₁, O₂, O₃ respectively.

C₁, C₂, C₃ touches line PQ at point A. Here PQ is the tangent at each circle.

If we join O₁, O₂, and O₃ to point A, then the line is perpendicular to line PQ because if we draw a line from the center to another circle at any point, then the tangent at that point is perpendicular to the radius.

But here, the line joining the centers does not bisect the line PQ because it depends on the length of PQ.

Hence, the given statement is False.

Question:9

Write ‘True’ or ‘False’, and justify your answer in each of the following.
If several circles pass through the endpoints P and Q of a line segment.
PQ, then their centers lie on the perpendicular bisector of PQ.

Answer:

According to the question.

Here, C₁ and C₂ circles pass through the points P and Q.

We know that the perpendicular bisector of the chord of a circle always passes through the center of the circle. Hence, the perpendicular bisector of line PQ passes through the center of the circles of C₁ and C₂.

Hence, the given statement is True.

Question:10

Write ‘True’ or ‘False’ and justify your answer in each of the following.
AB is the diameter of a circle and AC is its chord such that $\angle$BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.

Answer:

First of all, we solve the question according to the given conditions. If we can prove it, then it will be true otherwise, it will be false.

Given :$\angle$BAC = $30^{\circ}$

Diagram: Construct the figure according to the given conditions then join BC and OC.

To Prove: BC = BD

Proof :$\angle$BAC = $30^{\circ}$ (Given)

$\Rightarrow \, \angle BCD= 30^{\circ}$

[$\because$ angle between chord and tangent is equal to the angle made by chord in the alternate segment]

$\angle OCD= 90^{\circ}$

[$\because$ Radius and tangent’s angle is always $90^{\circ}$]

In $\bigtriangleup$OAC

OA = OC (both are the radius of the circle)

$\angle OCA= 30^{\circ}$

$\Rightarrow$ $\angle OCA= 30^{\circ}$ [opposite angles of an isosceles triangle is equal]

$\therefore \; \; \angle ACD= \angle ACO+\angle OCD$

$= 30+90= 120^{\circ}$

In $\bigtriangleup ACD$

$\angle CAD+\angle ADC+\angle DCA= 180^{\circ}$

[$\because$ sum of interior angle of a triangle $180^{\circ}$]

$30^{\circ}+\angle ADC+120^{\circ}= 180^{\circ}$

$\angle ADC= 180^{\circ}-120^{\circ}-30^{\circ}$

$\angle ADC=30^{\circ}$

In $\bigtriangleup$BCD we conclude that

$\angle BCD= 30^{\circ}$ and$\angle ADC=30^{\circ}$

$\Rightarrow$ $BC= BD$[$\because$sides which is opposite to equal angles is always equal]

Hence Proved.

Hence, the given statement is true.

Question:1

Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.

Answer:

According to the question

Given : AC = 8 CM

OC = 5 CM

AC = AB+BC

8 = BC+BC ($\because$ AB =BC)

BC = 4CM

In $\bigtriangleup OBC$ using Pythagoras theorem

$H^{2}+B^{2}+P^{2}$

$\left ( OC \right )^{2}= \left ( BC \right )^{2}+\left ( OB \right )^{2}$

$\left ( 5 \right )^{2}= \left ( 4 \right )^{2}+\left ( OB \right )^{2}$

$\left ( OB \right )^{2}= 25-16$

$OB= \sqrt{9}= 3cm$

Hence radius of the inner circle is 3 cm.

Question:2

Two tangents PQ and PR are drawn from an external point to a circle with center O. Prove that QORP is a cyclic quadrilateral.

Answer:

According to the question

To Prove: QORP is a cyclic quadrilateral.

OQ $\perp$ PQ, OR $\perp$ PR ($\because$ PQ, PR are tangents)

Hence, $\angle OQP+\angle ORP= 180^{\circ}\cdots (i)$

We know that the sum of the interior angles of the quadrilateral is $360^{\circ}$

$\angle OPQ+\angle OPR+\angle ORP+\angle ROQ= 360^{\circ}$ [Given (i)]

$180^{\circ}+\angle QPR+\angle ROQ= 360^{\circ}$

$\angle QPR+\angle ROQ= 180^{\circ}$

Here we found that the sum of opposite angles of a quadrilateral is $180^{\circ}$

Hence, QORP is a cyclic quadrilateral.

Hence proved

Question:3

If from an external point, B of a circle with center O, two tangents BC and BD are drawn such that $<$DBC = $120^{\circ}$, prove that BC + BD = BO, i.e., BO = 2BC.

Answer:

According to the question

Given : $\angle DBC= 120^{\circ}$

To Prove : BC + BD = BO, i.e., BO = 2BC

Here OC $\perp$ BC, OD $\perp$ BD ($\because$ BC, BD are tangents)

Join OB, which bisects $\angle DBC$

In $\bigtriangleup ODB$

$\cos \theta = \frac{B}{H}$

$\cos 60^{\circ}= \frac{BD}{OB}$

$\frac{1}{2}= \frac{BD}{OB}$

$OB= 2BD$

$OB= 2BC$ $\left ( \because BD= BC \, \ \ Tangents \right )$

$OB= BC+BC$

$OB= BC+BD\; \; \left ( \because BC= BD \right )$

Hence Proved

Question:4

Prove that the center of a circle touching two intersecting lines lies on the angle bisector of the lines.

Answer:

Here PQ and PR are tangents and O is the center of the circle.

Let us join OQ and OR.

Here $\angle OQP= \angle ORP= 90^{\circ}$

($\because$ tangent from exterior point is perpendicular to the radius through the point of contact)

In $\bigtriangleup$PQO and$\bigtriangleup$PRO

$OQ= OR$ (Radius of the circle)

$OP= OP$ (Common side)

Hence, $\bigtriangleup PQO\cong \bigtriangleup PRO$ [RHS interior]

Hence, $\angle RPO= \angle QPO$ [By CPCT]

Hence, O lies on the angle bisector of $\angle QPR$

Hence Proved.

Question:5

In the Figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.

Answer:

To Prove: AB = CD

Extend AB and CD then they meet at point E.

Here EA = EC ($\because$ length of tangent drawn from the same point is equal)

Also EB = ED ($\because$ length of tangent drawn from some point is equal)

AB = AE - BE

CD = CE -DF

From the equal axiom, if equals are subtracted from equals, then the result is equal.

$\therefore AB= CD$

Hence Proved.

Question:6

In the Figure, AB and CD are common tangents to two circles of unequal radii.

In the above question, if the radii of the two circles are equal, prove that AB = CD.

Answer:

To Prove AB = CD

According to the question

It is given that the radius of both circles is equal.

Hence, OA = OC = PB = PD

Here, $\angle A= \angle B= \angle C= \angle D= 90^{\circ}$

($\because$ tangent at any point is perpendicular to the radius at the point of contact)

Hence, ABCD is a rectangle.

Opposite sides of a rectangle are equal

$\therefore AB= CD$

Hence Proved.

Question:7

In the Figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.

Answer:

To Prove: AB = CD

We know that the length of tangents drawn from some point to a circle is equal.

So, EB = ED

AE = CE

Here AB = AE + EB

CD = CE + ED

From Euclid's axiom, if equals are added to equals, then the result is also equal.

$\therefore$ AB = CD

Hence Proved.

Question:8

A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.

Answer:

According to the question

To Prove: R bisects the arc PRQ

Here $\angle Q_{3}= \angle Q_{1}$ …..(i) ($\because$ Alternate interior angles)

We know that the angle between the tangent and chord is equal to the angle made by the chord in the alternate segment.

$\therefore \angle Q_{3}= \angle Q_{2}$ …..(ii)

From equations (i) and (ii)

$\angle Q_{1}= \angle Q_{2}$

We know that sides are opposite to equal angles and are equal.

$\therefore$ PR = QR

Hence, R bisects the arc PRQ

Hence Proved.

Question:9

Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.

Answer:

According to the question

To Prove :$\angle Q_{1}= \angle Q_{2}$

X₁, Y₁, X₂, and Y₂ are tangents at points A and B, respectively.

Take a point C and join AC and AB.

Now $\angle Q_{1}= \angle C$ …..(i) (Angle in alternate segment)

Similarly,

$\angle Q_{2}= \angle C$ …..(ii)

From equations (i) and (ii)

$\angle Q_{1}= \angle Q_{2}= \angle C$ …..(iii)

From equation (3)

$\angle Q_{1}= \angle Q_{2}$

Hence Proved.

Question:10

Prove that a diameter AB of a circle bisects all those chords that are parallel to the tangent at point A.

Answer:

According to the question

Let us take a chord EF || XY

Here $\angle XAO= 90^{\circ}$

($\because$ tangent at any point of the circle is perpendicular to the radius through the point of contact)

$\angle EGO= \angle XAO$ (Corresponding angles)

$\therefore \, \angle EGO= 90^{\circ}$

Thus AB bisects EF.

Hence AB bisects all the chords that are parallel to the tangent at point A.

Hence Proved.

Question:1

If a hexagon ABCDEF circumscribes a circle, prove that AB + CD + EF = BC + DE + FA.

Answer:

Given ABCDEF hexagon, circumscribe a circle.

To Prove : AB + CD + EF = BC + DE + FA

Proof: Here AR = AS [$\because$ length of tangents drawn from a point are always equal]

Similarly,

BS = BT

CT = CU

DU = DV

EV = EW

FW = FR

Now AB + CD + EF = (AS + SB) + (CU + UD) + (EW + WF)

= (AR + BT) + (CT + DV) + (EV + FR)

= (AR + FR) + (BT + CT) + (DV + EV)

Now, according to Euclid’s axio,m when equals are added in equals, then the result is also equal

$\Rightarrow$ AB + CD + EF = AF + BC + DE

i.e., AB + CD + EF = BC + DE + FA

Hence Proved.

Question:2

Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, and AB at D, E, and F, respectively, prove that BD = s – b.

Answer:

Given : BC = a, CA = b, AB = c

Here, AF = AE = Z1 ($\mathbb{Q}$ tangents drawn from an external point to the circle are equal in length)

$CE=CD=Z_{2}$

$BD=BF=Z_{3}$

Here AB + BC + CA = c + a + b

(AB + FB) + (BC + DC) + (CE + EA) = a + b + c

$\left ( AB+FB \right )+\left ( BC+DC \right )+\left ( CE+EA \right )= a+b+c$

$\left ( Z_{1} +Z_{3}\right )+\left ( Z_{3} +Z_{2}\right )+Z_{2} +Z_{1}= a+b+c$

$2\left ( Z_{1}+Z_{2} +Z_{3}\right )= a+b+c$

$2\left ( Z_{1}+Z_{2} +Z_{3}\right )= 2S$

$2\left ( Z_{1}+Z_{2} +Z_{3}\right )= 2S$

$\left ( a+b+c= 2s= perimeter\, of\, \bigtriangleup ABC \right )$

$Z_{1}+Z_{2}+Z_{3}= s$

$Z_{3}= s-\left ( Z_{1} +Z_{2}\right )$

-$\Rightarrow BD= s-b$ $\left [\because b= CE+EA= Z_{1}+Z_{2} \right ]$

Hence Proved

Question:3

From an external point P, two tangents, PA and PB are drawn to a circle with center O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of the triangle PCD.

Answer:

In this figure

CE = CA [$\because$ Tangents from an external point to a circle are equal in length]

Similarly,

DE = DB and PB = PA

Perimeter of DPCD

= PC + CD + PD

= PC + CE + ED + PD ($\because$ CD = CE + ED)

= PC + CA + DB + PD $\begin{bmatrix} \because CE= CA & \\ ED= DB& \end{bmatrix}$

= PA + PB [$\because$ PC + CA = PA and DB + PD = PB]

= PA + PA [$\because$ PB = PA]

= 2PA

= 2 × 10 [$\because$ PA = 10]

= 20 cm

Question:4

If AB is a chord of a circle with center O, AOC is a diameter and AT is the tangent at A as shown in Figure. Prove that $\angle$BAT = $\angle$ACB

Answer:

Here $\angle ABC= 90^{\circ}$ [ AC is a diameter line, $\therefore$ Angle in semi-circle formed, is $90^{\circ}$]

In $\bigtriangleup$ABC

$\angle CAB+\angle ABC+\angle BCA= 180^{\circ}$

[$\because$ sum of interior angles of a triangle is $180^{\circ}$]

$\angle CAB+\angle BCA= 180^{\circ}-90^{\circ}$ ......(I)

We know that the diameter of a circle is perpendicular to the tangent.

$\therefore CA\perp AT$

$\therefore \angle CAT= 90^{\circ}$

$\Rightarrow \angle CAB+\angle BAT= 90^{\circ}\cdots \left ( ii \right )$

Equating equations (i) and (ii,) we get

$\angle CAB+\angle BAT= \angle CAB+\angle BCA$

$\angle BAT= \angle BCA$

Hence Proved

Question:5

Two circles with centers O and O' of radii 3 cm and 4 cm, respectively, intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.

Answer:

Given: Radii of two circles are OP = 3 cm and ${O}'$, and the intersection points of two circles are P and Q. Here two tangents drawn at point P are OP and ${O}'$P

$\therefore \: \angle P= 90^{\circ}$

$3^{2}-x^{2}= \left ( NP \right )^{2}$

Also apply Pythagoras theorem in $\bigtriangleup PN{O}'$ we get

$\left ( P{O}' \right )^{2}= \left ( PN \right )^{2}+\left (N {O}' \right )^{2}$

$\left (4 \right )^{2}= \left ( PN \right )^{2}+\left (5-x \right )^{2}$

$16= \left ( PN \right )^{2}+\left (5-x \right )^{2}$

$16- \left (5-x \right )^{2}= \left ( PN \right )^{2}\cdots \left ( ii \right )$

Equating equations (i) and (ii), we get

$9-x^{2}= 16-\left ( 5-x \right )^{2}$

$9-x^{2}-16+\left ( 25+x^{2}-10x \right )= 0$

$\left [ \because \left ( a-b \right )^{2}= a^{2}+b^{2}-2ab \right ]$

$-7-x^{2}+\left ( 25+x^{2}-10x \right )= 0$

$-7-x^{2}+25+x^{2}-10x= 0$

$18-10x= 0$

$18= 10x$

$\frac{18}{10}= x$

$x= 1\cdot 8$

Put x = 1.8 in equation (i) we get

$9-\left ( 1\cdot 8 \right )^{2}= NP^{2}$

$9-3\cdot 24= NP^{2}$

$5\cdot 76= NP^{2}$

$NP= \sqrt{5\cdot 76}$

$NP= 2\cdot 4$

$P\mathbb{Q}= 2\times PN= 2\cdot 24= 4\cdot 8 cm$

Question:6

In a right triangle ABC in which $\angle$B = $90^{\circ}$, a circle is drawn with AB as the diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.

Answer:

Let O be the center of the given circle.

Suppose P meets BC at point R

Construction: Joinpoint P and B

To Prove: BR = RC

Proof:$\angle ABC= 90^{\circ}$ [Given]

In $\bigtriangleup$ABC

$\angle ABC+\angle BCA+\angle CAB= 180^{\circ}$ [ Sum of interior angle of a triangle is 180°]

$90^{\circ}+\angle 2+\angle 1= 180^{\circ}$

$\angle 1+\angle 2= 180^{\circ}-90^{\circ}$

$\angle 1+\angle 2= 90^{\circ}$

Also $\angle 4= \angle 1$ [ tangent and chord made equal angles in alternate segment]

$\Rightarrow \angle 4+\angle 2= 90^{\circ}\cdots \left ( i \right )$

$\angle APB= 90^{\circ}$ [ angle in semi-circle formed is 90°]

$\angle APB+\angle BPC= 180^{\circ}$

$\angle BPC= 180^{\circ}-90^{\circ}$

$\angle BPC= 90^{\circ}$

$\angle 4+\angle 5= 90^{\circ}\cdots \left ( ii \right )$

Equal equation (i) and (ii) we get

$\angle 4+\angle 2= \angle 4+\angle 5$

$\angle 2= \angle 5$

$PR= RC \, \cdots \left ( iii \right )$ [Side opposite to equal angles are equal]

Also, PR = BR …..(iv) [ tangents drawn to a circle from the external point are equal]

From equations (iii) and (iv)

BR = RC

Hence Proved.

Question:7

In Figure, tangents PQ and PR are drawn to a circle such that $\angle$RPQ = $30^{\circ}$. A chord RS is drawn parallel to the tangent PQ. Find the $\angle$RQS.

Answer:
In the given figure PQ and PR are two tangents drawn from an external point P.
$\therefore$ PQ = PR [$\mathbb{Q}$ lengths of tangents drawn from an external point to a circle are equal]
$\Rightarrow \angle PQR=\angle QRP$ [angles opposite to equal sides are equal]
In $\bigtriangleup$PQR
$\angle PQR+\angle QRP+\angle RPQ= 180^{\circ}$
[ sum of angles of a triangle is 180°]
$\angle PQR+\angle PQR+\angle RPQ= 180^{\circ}$
$\left [ \angle PQR= \angle QRP \right ]$
$2\angle PQR+30^{\circ}= 180^{\circ}$
$\angle PQR= \frac{180^{\circ}-30^{\circ}}{2}$
$\angle PQR= \frac{150^{\circ}}{2}$
$\angle PQR= 75^{\circ}$
SR||OP (Given)
$\therefore$ $\angle SRQ= \angle RQP= 75^{\circ}$ [Alternate interior angles]
Also $\angle PQR= \angle QRS= 75^{\circ}$ [Alternate segment angles]
In $\bigtriangleup$QRS
$\angle Q+\angle R+\angle S= 180^{\circ}$
$\angle Q+75^{\circ}+75^{\circ}= 180^{\circ}$
$\angle Q= 180^{\circ}-75^{\circ}-75^{\circ}$
$\angle Q= 30^{\circ}$
$\therefore \angle RQS= 30^{\circ}$

Question:8

AB is a diameter and AC is a chord of a circle with center O such that $\angle$BAC = $30^{\circ}$. The tangent at C intersects extended AB at point D. Prove that BC = BD.

Answer:

Given AB is the diameter and AC is a chord of a circle with center O.

$\angle BAC= 30^{\circ}$

To Prove: BC = BD

Construction: Join B and C

Proof :$\angle BCD= \angle CAB$[Angle is alternate segment]

$\angle BCD= 30^{\circ}\: \left [ Given \right ]$

$\angle BCD= 30^{\circ}\cdots \left ( i \right )$

$\angle ACB= 90^{\circ}$ [Angle in semi-circle formed is 90°]

In $\bigtriangleup$ABC

$\angle CAB+\angle ABC+\angle BCA= 180^{\circ}$ [Sum of interior angles of a triangle is 180°]

$30^{\circ}+\angle ABC+90^{\circ}= 180^{\circ}$

$\angle ABC= 180^{\circ}-90^{\circ}-30^{\circ}$

$\angle ABC= 60^{\circ}$

Also , $\angle ABC+\angle CBD= 180^{\circ}$ [Linear pair]

$\angle CBD= 180^{\circ}-60^{\circ}$

$\angle CBD= 120^{\circ}$

$\angle ABC= 60^{\circ}$

In $\bigtriangleup CBD$

$\angle CBD+\angle BDC+\angle DCB= 180^{\circ}$

$\angle BDC= 30^{\circ}\cdots \left ( ii \right )$

From equations (i) and (ii)

$\angle BCD= \angle BDC$

$\Rightarrow BC= BD$[$\because$ Sides opposite to equal angles are equal]

Hence Proved.

Question:9

Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the endpoints of the arc.

Answer:

Let the mid-point of the arc be C, and DCE be the tangent to the circle.

Construction: Join AB, AC, and BC.

Proof: In $\bigtriangleup$ABC

AC = BC

$\Rightarrow \, \angle CAB= \angle CBA\: \cdots \left ( i \right )$

[Sides opposite to equal angles are equal]

Here, DCF is a tangent line.

$\therefore \; \; \angle ACD= \angle CBA$ [ angle in alternate segments are equal]

$\Rightarrow \; \angle ACD= \angle CAB$ …..(ii) [From equation (i)]

But here $\angle ACD$ and $\angle CAB$ are alternate angles.

$\therefore$ equation (ii) holds only when AB||DCE.

Hence, the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the endpoints of the arc.

Hence Proved.

Question:10

In the Figure, the common tangent, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E, and O' are collinear.

Answer:

Construction: Join AO and OS

${O}'D$ and${O}'B$

In $\bigtriangleup E{O}'B$ and $\bigtriangleup E{O}'D$

${O}'D= {O}'B$ [Radius are equal]

${O}'E= {O}'E$ [Common side]

ED = EB [Tangents drawn from an external point to the line circle are equal in length]

$AE{O}'B\cong E{O}'D$ [By SSS congruence criterion]

$\Rightarrow \; \angle {O}'ED= \angle {O}'EB\, \cdots \left ( i \right )$

i.e., ${O}'E$ is bisector of$\angle BED$

Similarly, OE is the bisector of $\angle AEC$

In quadrilateral $DEB{O}'$

$\angle O'DE= \angle {O}'BE= 90^{\circ}$

$\Rightarrow \, \angle {O}'DE= \angle {O}'BE= 180^{\circ}$

$\therefore \angle DEB+\angle D {O}'B= 180^{\circ}\, \cdots \left ( ii \right )$ [$\mathbb{Q}DEB{O}'$ is cyclic quadrilateral]

$\angle AED+\angle DEB= 180^{\circ}$ [$\mathbb{Q}$ AB is a straight line]

$\angle AED+180^{\circ}-\angle D{O}'B= 180^{\circ}$ [From equation (ii)]

$\angle AED-\angle D{O}'B= 0$

$\angle AED-\angle D{O}'B\: \: \cdots \left ( iii \right )$

Similarly $\angle AED= \angle ADC\: \:\cdots \left ( iv \right )$

From equation (ii) $\angle DEB= 180^{\circ}-\angle D{O}'B$

Dividing both sides by 2

$\frac{\angle DEB}{2}= \frac{180^{\circ}-\angle D{O}'B}{2}$

$\angle DE{O}'= 90^{\circ}-\frac{1}{2}\angle D{O}'B\: \: \cdots \left ( v \right )$

$\left [ \because \, \frac{\angle DEB}{2}= \angle DE{O}' \right ]$

Similarly $\angle AEC= 180^{\circ}-\angle AOC$

Dividing both sides by 2

$\frac{1}{2}\angle AEC= 90^{\circ}-\frac{\angle AOC}{2}$

$\angle AEO= 90^{\circ}-\frac{1}{2}\angle AOC\; \cdots \left ( vi \right )$

$\left [\because \frac{1}{2}\angle AEC= \angle AEO \right ]$

Now $\angle AEO+\angle AED+\angle DE{O}'$

$= 90-\frac{1}{2}\angle AOC+\angle AED+90^{\circ}-\frac{1}{2}\angle D{O}'B$

$= \angle AED+180^{\circ}-\frac{1}{2}\left ( \angle D{O}'B+\angle AOC \right )$

$= \angle AED+180^{\circ}-\frac{1}{2} \left [ \angle AED+\angle AED \right ]$ [from equations (iii) and (iv)]

$= \angle AED+180^{\circ}-\frac{1}{2} \left [ 2\angle AED \right ]$

$=\angle AED+180^{\circ}-\angle AED$

$= 180^{\circ}$

$\therefore \: \angle AED+\angle DE{O}'+\angle AEO= 180^{\circ}$

So, OEO’ is a straight line

$\therefore$ O, E and ${O}'$ are collinear.

Hence Proved

Question:11

In Figure. O is the center of a circle of radius 5 cm, T is a point such that OT = 13 cm, and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.

Answer:

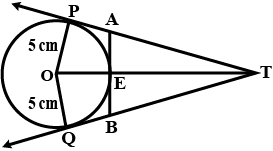
Given: Radius = 5 cm, OT = 13 cm

$OP\perp PT$ [ PT is tangent]

Using Pythagoras theorem $\bigtriangleup$OPT

$H^{2}+B^{2}+P^{2}$

$\left ( OT \right )^{2}= \left ( OP \right )^{2}+\left ( PT \right )^{2}$

$\left ( 13 \right )^{2}= \left ( 5 \right )^{2}+\left ( PT \right )^{2}$

$\left ( PT \right )^{2}= 169-25$

$PT= {\sqrt{144}}= 12\, cm$

PT and QT are tangents from the same point

$\therefore$ PT = QT = 12 cm

AT = PT – PA

AT = 12 – PA ..…(i)

Similarly BT = 12 – QB ..…(ii)

Since PA, PF, and BF, BQ are tangents from points A and B, respectively.

Hence, PA = AE ..…(iii)

BQ = BE ..…(iv)

AB is tangent at point E

Hence OE $\perp$ AB

$\angle AET= 180^{\circ}-\angle AEO$ $\left ( \because \, \angle AEO= 90^{\circ} \right )$

$\angle AET= 180^{\circ}-90^{\circ}$

$\angle AET= 90^{\circ}$

ET = OT – OF

ET = 13 – 5

ET = 8 cm

In $\bigtriangleup$AET, using Pythagoras theorem

$\left ( H \right )^{2}= \left ( B \right )^{2}+\left ( P \right )^{2}$

$\left ( AT \right )^{2}= \left ( AE \right )^{2}+\left ( ET \right )^{2}$

$\left ( 12-PA \right )^{2}= \left ( PA \right )^{2}+\left ( 8 \right )^{2}$ [using (i) and (ii)]

$144+\left ( PA \right )^{2}-24\left ( PA \right )-\left ( PA \right )^{2}-64= 0$

$\left [ \because \left ( a-b \right )^{2}= a^{2}+b^{2}-2ab \right ]$

$80-42\left ( PA \right )= 0$

$24\left ( PA \right )= 80$

$\left ( PA \right )= \frac{80}{24}= \frac{10}{3}\, cm$

$\therefore \; AE= \frac{10}{3}\, cm\, \left [ using\left ( iii \right ) \right ]$

Similiraly $BE= \frac{10}{3}\, cm$

$AB= AE+BE= \frac{10}{3}+\frac{10}{3}= \frac{20}{3}\, cm$

Question:12

The tangent at point C of a circle and a diameter AB when extended intersect at P. If $\angle$PCA =$110^{\circ}$ , find $\angle$CBA [see Figure].

Answer:
Given : $\angle PCA= 110^{\circ}$
Here $\angle PCA= 90^{\circ}$[$\because$ PC is tangent]

$\angle PCA= \angle PCO+\angle OCA$

$110^{\circ}= 90^{\circ}+\angle OCA$

$\angle OCA= 20^{\circ}$

Here OC = OA (Radius)

$\therefore \: \angle OCA= \angle OAC= 20^{\circ}\cdots \left ( i \right )$ [$\because$ Sides opposite to equal angles are equal]

We know that PC is tangent and angles in alternate segments are equal.

Hence $\angle BCP= \angle CAB= 20^{\circ}$

In $\bigtriangleup OAC$

$\angle O+\angle C+\angle A= 180^{\circ}$ [Interior angles sum of triangle is 180°]

$\angle O+20^{\circ}+20^{\circ}= 180^{\circ}$ [using (i)]

$\angle O= 180^{\circ}-40^{\circ}= 140^{\circ}$…..(ii)

Here $\angle COB+\angle COA= 180^{\circ}$

$\angle COB= 180^{\circ}-140^{\circ}$( using (ii))

$\angle COB= 40^{\circ}$ …..(iii)

In $\bigtriangleup COB$

$\angle C+\angle O+\angle B= 180^{\circ}$ [using (iii)]

$90^{\circ}-20^{\circ}+40^{\circ}+\angle B= 180^{\circ}$

$\angle B= 180^{\circ}-110^{\circ}= 70^{\circ}$

Hence $\angle CBA= 70^{\circ}$

Question:13

If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.

Answer:

According to the question

In $\bigtriangleup ABD$ and $\bigtriangleup ACO$

AB = AC [Given]

BO = CO [Radius]

AO = AO [Common side]

$\therefore \, \bigtriangleup ABO\cong \bigtriangleup ACO$ [By SSS congruence Criterion]

$\angle Q_{1}= \angle Q_{2}$ [CPCT]

In $\bigtriangleup ABD$ and $\bigtriangleup ACD$

AB = AC [given]

$\angle Q_{1}= \angle Q_{2}$

AD = AD [common side]

$\therefore \bigtriangleup ABD\cong \bigtriangleup ACD$ [By SAS congruence Criterion]

$\angle ADB= \angle ADC$ …..(i) [CPCT]

$\angle ADB= \angle ADC= 180^{\circ}$ …..(ii)

From (i) and (ii)

$\angle ADB= 90^{\circ}$

OA is a perpendicular that bisects chord BC

Let AD = x, then OD = 9 – x $\left ( \because OA= 9\, cm \right )$

Use Pythagoras in $\bigtriangleup$ADC

$\left ( AC \right )^{2}= \left ( AD \right )^{2}+\left ( DC \right )^{2}$

$\left ( 6 \right )^{2}= x^{2}+\left ( DC \right )^{2}$

$\left ( AC \right )^{2}= 36-x^{2}$ …..(iii)

In $\bigtriangleup$ODC using Pythagoras theorem

$\left ( OC \right )^{2}= \left ( OD \right )^{2}+\left ( DC \right )^{2}$

$\left ( DC \right )^{2}= 81-\left ( 9-x \right )^{2}$ …..(iv)

From (iii) and (iv)

$36-x^{2}= 81-\left ( 9-x \right )^{2}$

$36-x^{2}- 81+\left ( 81+x^{2} -18x\right )= 0$

$\left [ \because \left ( a-b \right )^{2} +a^{2}+b^{2}-2ab\right ]$

$36-x^{2}-81+81+x^{2}-18x= 0$

$18x= 36$

$x= 2$

i.e., AD = 2 cm, OD = 9 – 2 = 7 cm

Put the value of x in (iii)

$\left ( DC \right )^{2}= 36-4$

$\left ( DC \right )^{2}= 32$

$DC= 4\sqrt{2}\, cm$

$BC= BD+DC$

$BC= 2DC$ $\left [ \because BD= DC \right ]$

$BC= 8\sqrt{2}\, cm$

Areao of $\bigtriangleup ABC= \frac{1}{2}\times base\times height$

$= \frac{1}{2}\times \times 8\sqrt{2}\times 2= 8\sqrt{2}\, cm$

Question:14

A is a point at a distance 13 cm from the center O of a circle of radius 5 cm.AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the $\bigtriangleup$ABC.

Answer:

Let us make a figure according to the question

Given : OA = 13 cm, Radius = 5 cm

Here AP = AQ (tangent from the same point)

OP $\perp$ PA, OQ $\perp$ QA ( AP, AQ are tangents)

In $\bigtriangleup$OPA using Pythagoras theorem

$\left ( H \right )^{2}= \left ( B \right )^{2}+\left ( P \right )^{2}$

$\left ( QP \right )^{2}= \left ( OP \right )^{2}+\left ( PA \right )^{2}$

$\left ( 13 \right )^{2}= \left ( 5 \right )^{2}+\left ( PA \right )^{2}$

$\left ( PA \right )^{2}= 169-25$

$PA= \sqrt{144}= 12\, cm$ ........(i)

Perimeter of $\bigtriangleup$ABC = AB + BC + CA

= AB + BR + RC + CA

= AB + BD + CQ + CA

[ BP and BR are tangents from point B and CP and CQ are tangents from point C]

= AP + AQ [ AP = AB + BP, AQ = AC + CQ]

= AP + AP [ AP = AQ]

= 2AP

= 2 × 12 [using (i)]

= 24 cm

NCERT Exemplar Solutions Class 10 Maths Chapter 9 Important Topics:

• Several theorems about a tangent to the circle and their proofs.
• To find the number of tangents that can be drawn from any given point
• In this chapter, students will learn that the tangent will be perpendicular to the line joining the centre and the point of tangent on the circle.
• Class 10 Maths NCERT exemplar chapter 9 solutions discuss the method that if we draw two tangents on diametrically opposite points of a circle, we will observe that these two tangents are parallel.

NCERT Class 10 Exemplar Solutions for Other Subjects:

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science solutions

NCERT Class 10 Maths Exemplar Solutions for Other Chapters:

Importance of NCERT Exemplar Class 10 Maths Solutions Chapter 9:

These Class 10 Maths NCERT exemplar Chapter 9 solutions provide an extension to the learning of circles done in Class 9. The chapter discusses tangents at any point of the circle along with the theorems such as the perpendicular tangent theorem. The chapter on Circles can be better understood and practiced using these NCERT exemplar Class 10 Maths chapter 9 solutions Circles, and will be enough to solve other books such as A textbook of Mathematics by Monica Kapoor, NCERT Class 10 Maths, RD Sharma Class 10 Maths, RS Aggarwal Class 10 Maths etc.

Some important facts about solving circles in class 10 are listed below.

• Students can study strategically at their own pace after accessing Class 10 Maths NCERT Solutions chapter 9. This will boost their confidence to attempt other questions from this chapter.

• Class 10 Maths Chapter 9 NCERT solutions are solved by subject-matter experts and are very reliable at the same time. The solutions provide shortcuts as well as detailed explanations with necessary formulae that will help students to understand the answers better.

• These solutions will help students manage their time efficiently in this chapter and understand which questions are easier to approach and which are time-consuming. This will be helpful during the exam

Check Chapter-Wise Solutions of Book Questions

Read NCERT Solution Subject Wise

Given below are the subject-wise exemplar solutions of class 10 NCERT:

• NCERT Solution for Class 10 Science
• NCERT Solution for Class 10 Maths

Check NCERT Notes Subject Wise

Given below are the subject-wise NCERT Notes of class 10 :

• NCERT Notes for Class 10 Science
• NCERT Notes for Class 10 Maths

Also, check the NCERT Books and the NCERT Syllabus here

Here are some useful links for NCERT books and the NCERT syllabus for class 10:

• NCERT Books Class 10 Maths
• NCERT Syllabus Class 10 Maths
• NCERT Books Class 10
• NCERT Syllabus Class 10