• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Exemplar Class 10 Maths Solutions Chapter 6 Triangles

NCERT Exemplar Class 10 Maths Solutions Chapter 6 Triangles

Edited By Ravindra Pindel | Updated on Sep 05, 2022 03:42 PM IST | #CBSE Class 10th

NCERT exemplar Class 10 Maths solutions chapter 6 provides the understanding for triangles and the similarity of triangles. It is the first chapter under the unit: Geometry of Class 10. The solutions available under NCERT exemplar Class 10 Maths chapter 6 solutions have been prepared and compiled by our subject matter experts of mathematics with cumulative experience of more than 10 years and equips the student to study NCERT Class 10 Maths effortlessly. These Class 10 Maths NCERT exemplar chapter 6 solutions provide step-by-step detailed solutions to enhance the learning of concepts based on Triangles. The CBSE Syllabus for Class 10 is the building block for these NCERT exemplar Class 10 Maths solutions chapter 6.

This Story also Contains
  1. NCERT Exemplar Class 10 Maths Solutions Chapter 6: Exercise-6.1
  2. NCERT Exemplar Class 10 Maths Solutions Chapter 6: Exercise-6.2
  3. NCERT Exemplar Class 10 Maths Solutions Chapter 6: Exercise-6.3
  4. NCERT Exemplar Class 10 Maths Solutions Chapter 6: Exercise-6.4
  5. NCERT Exemplar Class 10 Maths Chapter 6 Solutions Important Topics:
  6. NCERT Class 10 Exemplar Solutions for Other Subjects:
  7. NCERT Class 10 Maths Exemplar Solutions for Other Chapters:
  8. Features of NCERT Exemplar Class 10 Maths Solutions Chapter 6:

NCERT Exemplar Class 10 Maths Solutions Chapter 6: Exercise-6.1

Question:1

In Fig., \angle BAC=90^{o} and AD\perp BC. Then,

(a) BD.CD=BC^{2}
(b) AB.AC=BC^{2}
(c) BD.CD=AD^{2}
(d) AB.AC=AD^{2}

Answer:

Given :- \angle BAC=90^{o}
First of all we have find \angle DBA and \angle DAC in triangles ABD and ADC respectively
In \Delta ABD and \angle ADC
\angle ADB=90^{o}
\angle ADC=90^{o}
In \Delta ABC
\angle BAC=90^{o} (given)
Now let us find angle CAD from triangle ADC
Here \angle ADC+\angle DCA+\angle CAD=180^{o}
(sum of interior angles of triangle = 180o)
90^{o}+\angle C+\angle CAD=180^{o}
\angle CAD=180^{o}-90^{o}-\angle C
\angle CAD=90^{o}-\angle C \; \; \; \; \; \; \; \; \; \; \; \; \; ....(1)
Now let us find angle DBA using triangle ABC
Here \angle ABC+\angle BCA+\angle CAB=180^{o}
{sum of interior angles of triangle = 180o}
\angle ABC+\angle C+90^{o}=180^{o}
\angle ABC=90^{o}-\angle C
\angle ABC=\angle DBA=90^{o}-\angle C \; \; \; \; \; \; \; ...(2)
In \Delta ABD and \Delta ADC we get
\angle ADB=\angle ADC {90o each}
AD=AD {common side}
\angle CAD=\angle DBA {from equation (1) and (2) it is clear that both is 90^{o}-\angle C}
\therefore \Delta ABD\sim \Delta ADC (by ASA similarity)
\therefore \frac{BD}{AD}=\frac{AD}{CD}
BD.CD=AD.AD {by cross multiplication}
BD.CD=AD^{2}
Hence option (C) is correct.

Question:2

The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is
(A) 9 cm
(B) 10 cm
(C) 8 cm
(D) 20 cm

Answer:

Answer : [B]

Here ABCD is a rhombus and we know that diagonals of a rhombus are perpendicular bisector of each other
Given: AC=16 \; cm and BD=12 \; cm
\Rightarrow AO=\frac{AC}{2}=\frac{16}{2}=8\; cm
also BO=\frac{BD}{2}=\frac{12}{2}=6\; cm and \angle AOB=90^{o}
Using Pythagoras theorem in \Delta AOB we get
AB^{2}=AO^{2}+OB^{2}
AB^{2}=8^{2}+6^{2}
AB^{2}=64+36
AB^{2}=100
AB=\sqrt{100}
AB=10\; cm
Hence option (B) is correct

Question:3

If \Delta ABC \sim \Delta EDF and \Delta ABC is not similar to \Delta DEF, then which of the following is not true?
(A) BC . EF = A C. FD (B) AB . EF = AC . DE
(C) BC . DE = AB . EF (D) BC . DE = AB . FD

Answer:

Answer : [C]
Given : \Delta ABC\sim \Delta EDF
\therefore \frac{AB}{ED}=\frac{BC}{DF}=\frac{AC}{EF}
Taking the first two terms we get
\therefore \frac{AB}{ED}=\frac{BC}{DF}
by cross multiply we get
AB.DF=BC.ED
Hence option D is correct
Now taking the last two terms we get
\frac{BC}{DF}=\frac{AC}{EF}\Rightarrow BC.EF=DF.AC {By cross multiplication}
Hence option (A) is also correct
Now taking first and last terms, we get
\frac{AB}{ED}=\frac{AC}{EF}\Rightarrow AB.EF=AC.ED {By cross multiplication}
Hence option (B) is also correct
By using congruence properties we conclude that only option C is not true.

Question:4

If in two triangles ABC and PQR, \frac{AB}{QR}=\frac{BC}{PR}=\frac{CA}{PQ}, then
(a) \Delta PQR\sim \Delta CAB
(b) \Delta PQR\sim \Delta ABC
(c) \Delta CBA\sim \Delta PQR
(d) \Delta BCA\sim \Delta PQR

Answer:

Answer: [A]
In \Delta ABC and \Delta PQR
\frac{AB}{QR}=\frac{BC}{PR}=\frac{CA}{PQ}\; \; \; \; \; \; \; .......(1)
(A) If \Delta PQR \sim \Delta CAB

Here; \frac{CA}{PQ}=\frac{CB}{PR}=\frac{AB}{PQ}
It matches the equation (1) Hence option A is correct.
(B) If \Delta PQR \sim \Delta ABC

Here; \frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR}
It does not match equation (1)
Therefore option (B) is not correct.
(c) \Delta CBA\sim \Delta PQR

Here; \frac{CB}{PQ}=\frac{BA}{QR}=\frac{CA}{PR}
It does not match equation (1) Hence option (C) is not correct
(D) \Delta BCA \sim \Delta PQR

Here; \frac{BC}{PQ}=\frac{CA}{QR}=\frac{BA}{PR}
It does not match the equation (1). Hence option (D) is not correct.

Question:5

In Fig., two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, \angle APB=50^{o} and \angle CDP=30^{o}. Then, \angle PBA is equal to

(A) 50° (B) 30° (C) 60° (D) 100°

Answer:

Answer: [D]
In \Delta APB and \Delta CPD.
\frac{AP}{PD}=\frac{6}{5}
\frac{BP}{CP}=\frac{3}{2.5}=\frac{30}{25}=\frac{6}{5}
\angle APB=\angle CPD=50^{o} {vertically opposite angles}
\therefore \Delta APB \sim \Delta DPC {By SAS similarity criterion}
\therefore \angle A=\angle D=30^{o} {corresponding angles of similar triangles}
In \Delta APB
\angle A+\angle B+\angle APB=180^{o} {Sum of interior angles of a triangle is 180°}
30^{o}+\angle B+50^{o}=180^{o}
\angle B=180^{o}-50^{o}-30^{o}
\angle B=100^{o}
\Rightarrow \angle PBA=100^{o}
Hence option D is correct.

Question:6

If in two triangles DEF and PQR, \angle D = \angle Q \; \text {and} \; \angle R = \angle E, then which of the following is not true?
(a) \frac{EF}{PR}=\frac{DF}{PQ}
(b) \frac{DE}{PQ}=\frac{EF}{RP}
(c) \frac{DE}{QR}=\frac{DF}{PQ}
(d) \frac{EF}{RP}=\frac{DE}{QR}

Answer:

Answer : [B]
In \Delta DEF and \Delta PQR
\angle D=\angle Q and \angle R=\angle E
Now draw two triangles with the help of given conditions:-

Here \angle D=\angle Q and \angle E=\angle R {Given}
\therefore \; \; \; \; \Delta DEF\sim \Delta QRP {by AA similarity}
\Rightarrow \angle F=\angle P {corresponding angles of similar triangles}
\therefore \frac{DF}{QP}=\frac{ED}{RQ}=\frac{FE}{PR}\; \; \; \; \; \; \; \; ....(1)
Here option (A) \frac{EF}{PR}=\frac{DF}{PQ} is true because both the terms are derived from equation (1)
Here option (B) \frac{DE}{PQ}=\frac{EF}{RP} is not true because the first term is not derived from equation (1)
Here option (C) \frac{DE}{QR}=\frac{DF}{PQ} is true because both the terms are derived from equation (1)
Here option D i.e. is also true because both terms are derived from equation (1)
Hence option (B) is not true.

Question:7

In triangles ABC \; \text {and} \; DEF, \angle B = \angle E, \angle F = \angle C \; \text {and}\; AB = 3 DE. Then, the two triangles are
(A) congruent but not similar (B) similar but not congruent
(C) neither congruent nor similar (D) congruent as well as similar

Answer:

Answer : [B]
In \Delta ABC and \Delta DEF
\angle B=\angle E\; \text {and}\; \angle F=\angle C\; \text {also}\; AB=3DE

In \Delta ABC and \Delta DEF
\angle B=\angle E (given)
\angle F=\angle C (given)
\angle A=\angle D (third angle)
Therefore \Delta ABC\sim \Delta DEF (by AAA similarity)
Also, it is given that AB=3DE
\Rightarrow AB\neq DE
Hence \Delta ABC and \Delta DEF is not congruent because congruent figures have the same shape and same size.
Therefore the two triangles are similar but not congruent.

Question:8

It is given that \Delta ABC\sim \Delta PQR, with \frac{BC}{QR}=\frac{1}{3}. then \frac{ar\left ( PRQ \right )}{ar\left ( BCA \right )} is equal to
(a) 9
(b) 3
(c) \frac{1}{3}
(d) \frac{1}{9}

Answer:

Answer : [A]
Given : \Delta ABC\sim \Delta PQR
\frac{BC}{QR}=\frac{1}{3}

It is given that \Delta ABC\sim \Delta PQR
\therefore \frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR}\; \; \; \; \; \; ...(1) \therefore \frac{ar(PRQ)}{ar(BCA)}=\frac{PR^{2}}{AC^{2}}
[Q If triangles are similar their areas are proportional to the squares of the corresponding sides.]
\Rightarrow \frac{ar(PRQ)}{ar(BCA)}=\frac{QR^{2}}{BC^{2}}\; \; \; \; \; \; \; ...(2) \text{{using equation (1)}}
\frac{QR}{BC}=\frac{3}{1} \; \; \; \; \; \; \; \; \; \left \{ \because \frac{BC}{QR}=\frac{1}{3} \right \}
\text{Put} \frac{QR}{BC}=\frac{3}{1} \text{in (2) we get}
\therefore \frac{ar(PRQ)}{ar(BCA)}=\frac{3^{2}}{1^{2}}=\frac{9}{1}=9
Hence option A is correct.

Question:9

It is given theat \Delta ABC\sim \Delta DFE,\angle A=30^{o},\angle C=50^{o},AB=5\; cm,AC=8\; cm and DF=7.5\; cm. then the following is true ?
(A)DE=12\; cm,\angle E=50^{o}
(B) DE=12\; cm,\angle F=100^{o}
(C) EF=12\; cm,\angle D=100^{o}
(D) EF=12\; cm,\angle D=30^{o}

Answer:

Answer: [A]
\Delta ABC \sim \Delta DEF
\angle A=30^{o},\angle C=50^{o}
AB=5\; cm,AC=8\; cm,DF=7.5\; cm

\Delta ABC \sim \Delta DEF
\therefore \angle A=\angle D=30^{o}
\angle C=\angle E=100^{o}
\frac{AB}{DF}=\frac{BC}{FE}=\frac{AC}{DE}\; \; \; \; \; \; \; \; ....(1)
In\Delta ABC
\angle A+\angle B+\angle C=180^{o}
30+\angle B+100^{o}=180^{o}
\angle B=180^{o}-100^{o}-30^{o}
\angle B=50^{o}
\Rightarrow \angle B=\angle E=50^{o} \left \{ \because \Delta ABC\sim \Delta DFE \right \}
Now equate first and the last term of equation (1) we get
\frac{AB}{DF}=\frac{AC}{DE}
\frac{5}{7.5}=\frac{8}{DE}
DE=\frac{8 \times 75}{50}=12\; cm

Question:10

If in triangle ABC and DEF ,\frac{AB}{DE}=\frac{BC}{FD}, then they will be similar when
\text{(A)} \angle B=\angle E
\text{(B)} \angle A=\angle D
\text{(C)} \angle B=\angle D
\text{(D)} \angle A=\angle D

Answer:

Answer : [C]
Given :
\frac{AB}{DE}=\frac{BC}{FD}
Here corresponding sides of given triangles ABC and DEF are equal in ratio, therefore, the triangles are similar
Also, we know that if triangles are similar then their corresponding angles are equal
\Rightarrow \angle A=\angle E
\angle B=\angle D
\angle C=\angle F
Hence option C is correct.

Question:11

\text{If }\Delta ABC\sim \Delta QRP,\frac{ar(ABC)}{ar(PQR)}=\frac{9}{4},AB=18\; cm and BC = 15 cm then PR is equal to ?
\text{(A)} 10\; cm
\text{(B)} 12\; cm
\text{(C)} \frac{20}{3}\; cm
\text{(D)} 8\; cm

Answer:

Answer : [A]

\Delta ABC \sim \Delta QRP \; \text {and}\; AB = 18 \; cm, BC = 15 \; cm
\therefore \frac{AC}{PQ}=\frac{AB}{QR}=\frac{BC}{RP}
\frac{ar(ABC)}{ar\left ( PQR \right )}=\frac{BC^{2}}{RP^{2}}\; \; \; \; \; \; \; \; ....(1)
[Q If triangles are similar, their areas are proportional to the squares of the corresponding sides.]
\frac{ar(ABC)}{ar\left ( PQR \right )}=\frac{9}{4}
[Using equation (1)]
\Rightarrow \frac{BC^{2}}{RP^{2}}=\frac{9}{4}
\frac{(15)^{2}}{RP^{2}}=\frac{9}{4}
RP^{2}=\frac{225\times 4}{9}=100
RP=\sqrt{100}
RP=10\; cm


Question:12

If S is a point on side PQ of a triangle PQR such that PS = QS = RS, then
(A)PR .QR = RS^{2} (B)QS^{2} + RS^{2} = QR^{2}
(C) PR^{2} + QR^{2} = PQ^{2} (D) PS^{2} + RS^{2} = PR^{2}

Answer:

Answer : [C]
Given: In triangle PQR
PS = QS = RS
\Rightarrow PS = RS
\therefore \angle 1=\angle 2 ...(1)
(Q If a right angle triangle have equal length of base and height then their acute angles are also equal)
\text{Similarly} \angle 3=\angle 4 ...(2)
( Q corresponding angles of equal sides are equal)
\text{In }\Delta PQR
\angle P+\angle Q+\angle R=180^{o}
\because sum of angles of a triangle is 180°
\angle 2+\angle 4+\angle 1+\angle 3=180^{o} ....(3)
Using equation (1) and (2) in (3)
\angle 1+\angle 3+\angle 1+\angle 3=180
2\left ( \angle 1+\angle 3 \right )=180^{o}
\Rightarrow \angle R=90^{o}
\text{Here }\angle R=90^{o}\therefore \Delta PQR \text{is right angle triangle }
PR^{2} + QR^{2} = PQ^{2}

NCERT Exemplar Class 10 Maths Solutions Chapter 6: Exercise-6.2

Question:1

Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.

Answer:

Answer : [False]
Sides of the triangle are 25cm, 5 cm and 24 cm
According to Pythagoras theorem, the square of the hypotenuse of a right-angle triangle is equal to the sum of the square of the remaining two sides.
\Rightarrow \left ( 25 \right )^{2}=\left ( 5 \right )^{2}+\left ( 24 \right )^{2}
625=25+576
625 \neq 601
Hence the given statement is false.
The triangle with sides 25 cm, 5 cm and 24 cm is not a right-angle triangle.

Question:2

\text{It is given that} \Delta DEF\sim \Delta RPQ. \text{is it true to say that} \angle D = \angle R \text{and} \angle F = \angle P ? Why?

Answer:

Answer : [False]
Given : \Delta DEF \sim \Delta RPQ
If two triangles are similar, then their corresponding angles are equal and their corresponding sides are in the same ratio

i.e.
\frac{DE}{RP}=\frac{EF}{PQ}=\frac{DF}{RQ}
and their angles are also equal that is
\angle D=\angle R
\angle E=\angle P
\angle F=\angle Q
\text{In the given statement} \angle D = \angle R \text{and} \angle F = \angle P
\text{But according to properties of a similar triangle} \angle F \neq \angle P \text{that is }. \text{Hence the given statement is false. }

Question:3

A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR= 6 cm and PB = 4 cm. Is AB || QR?
Give reasons for your answer.

Answer:

Answer : [True]

Given: PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm
QA = QP – PA = 12.5 – 5 = 7.5 cm
\frac{PA}{AQ}=\frac{5}{7.5}=\frac{50}{75}=\frac{2}{3}
\frac{PB}{PR}=\frac{4}{6}=\frac{2}{3}
Here
\frac{PA}{AQ}=\frac{PB}{PR}
According to Converse of basic proportionality theorem if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
\therefore AB\parallel QR

Question:4

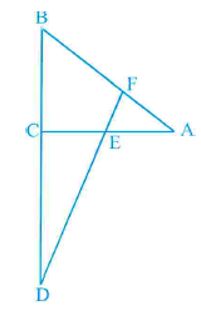
In Fig 6.4, BD and CE intersect each other at the point P. Is \DeltaPBC \sim \DeltaPDE? Why?

Answer:

Answer : [True]
Given:- BD and CE intersect each other at point P.
\text{Here, } \angle BPC=\angle EPD \text{[Vertically opposite angle] }
\frac{BP}{PD}=\frac{5}{10}=\frac{1}{2}
\frac{PC}{PE}=\frac{6}{12}=\frac{1}{2}
\frac{BP}{PD}=\frac{PC}{PE}
Two triangles are similar if their corresponding angles are equal and their corresponding sides are in the same ratio.
\text{Also in } \Delta PBC \text{ and }\Delta PDE
\frac{BP}{PD}=\frac{PC}{PE}\; and\; \angle BPC=\angle EPD
\therefore \Delta PBC\sim \Delta PDE
Hence given statement is true.

Question:5

In triangles PQR and MST, \angleP = 55°, \angleQ = 25°, \angleM = 100° and \angleS = 25°. Is \DeltaQPR \sim \DeltaTSM? Why?

Answer:

Answer: [False]

\Delta PQR, \angle P + \angle Q + \angle R = 180^{o}\text{ ({Interior angle of triangle}) }
55+25+\angle R=180
\angle R=180-80
\angle R=100^{o}
\text{In } \Delta TSM, \angle T + \angle S + \angle M = 180^{o}\text{[Interior angle of the triangle] }
\angle T + 25^{o}+100^{o}=180^{o}
\angle T =180^{o}-125
\angle T =55^{o}
\text{In } \Delta PQR \text{and } \Delta TSM
\angle P=\angle T
\angle Q=\angle S
\angle R=\angle M
Also are know that if all corresponding angles of two triangles are equal then triangles are similar.
\therefore \Delta PQR\sim \Delta TSM
Hence given statement is false because \angleQPR is not similar to \angleTSM.

Question:6

Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.

Answer:

Answer: [False]
Quadrilateral:- A quadrilateral can be defined as a closed, two-dimensional shape which has four straight sides. We can find the shape of quadrilaterals in various things around us, like in a chessboard, a kite etc. The given statement "Two quadrilaterals are similar if their corresponding angles are equal" is not true because. Two quadrilaterals are similar if and only if their corresponding angles are equal and the ratio of their corresponding sides are also equal.

Question:7

Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?

Answer:

Answer: True

According to question,
AB = 3PQ \; \; \; \; \; \; ...(1)
AC = 3PR \; \; \; \; \;...(2)
also the perimeter of \DeltaABC is three times the perimeter of \DeltaPQR
AB + BC + CA = 3(PQ + QR + RP)

AB + BC + CA = 3PQ + 3QR + 3RP

3PQ + BC + 3PR = 3PQ + 3QR + 3PR (using eq. (1) and (2))

BC=3QR\; \; \; \; \; \; .....(3)
from equation (1), (2) and (3) we conclude that sides of both the triangles are in the same ratio.
As we know that if the corresponding sides of two triangles are in the same ratio, then the triangles are similar by SSS similarity criterion
Hence given statement is true.

Question:8

If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?

Answer:

Answer : [True]
Let two right angle triangles are ABC and PQR.

Given:- One of the acute angle of one triangle is equal to an acute angle of the other triangle.
\text {In}\Delta ABC \; \text {and}\; \Delta PQR
\\\angle B = \angle Q = 90^{o}\\\angle C = \angle R = x^{o}
In \Delta ABC
\angle A + \angle B + \angle C = 180^{o}
[Sum of interior angles of a triangle is 180°]
\angle A + 90^{o}+ x^{o} = 180^{o}
\angle A + 90^{o}- x^{o} \; \; \; \; \; \; \; \; \; ....(1)
Also in \Delta PQR
\angle P + \angle Q + \angle R = 180^{o}
\angle P + 90^{o}- x^{o} = 180^{o}
\angle P = 90^{o}- x^{o} \; \; \; \; \; \; .....(2)
from equation (1) and (2)
\angle A=\angle P \; \; \; \; \; \; .....(3)
from equation (1), (2) and (3) are observed that corresponding angles of the triangles are equal therefore triangle are similar.

Question:9

The ratio of the corresponding altitudes of two similar triangles is 3/5. Is it correct to say that ratio of their areas is 6/5? Why?

Answer:

Answer: [False]
Given:- Ratio of corresponding altitudes of two similar triangles is 3/5
As we know that the ratio of the areas of two similar triangles is equal to the ratio of squares of any two corresponding altitudes.
\therefore \frac{\text {Area 1}}{\text {Area 2}}=\left ( \frac{\text {Altitude 1}}{\text {Altitude 2}} \right )^{2}
\frac{\text {Area 1}}{\text {Area 2}}=\left ( \frac{3}{5} \right )^{2} \left [ Q\frac{\text {Altitude 1}}{\text {Altitude 2}}=\frac{3}{5} \right ]
=\frac{9}{25}
Hence the given statement is false because ratio of areas of two triangles is 9/25 which is not equal to 6/5

Question:10

D is a point on side QR of \DeltaPQR such that PD \perp QR. Will it be correct to say that \DeltaPQD ~ \DeltaRPD? Why?

Answer:

Answer : [False]

In \DeltaPQD and \DeltaRPD
PD = PD (common side)
\angle PDQ = \angle PDR (each 90o)
The given statement \Delta PQD \sim \Delta RPD is false.
Because according to the definition of similarity two triangles are similar, if their corresponding angles are equal and their corresponding sides are in the same ratio

Question:11

In Fig., if \angleD = \angleC, then is it true that \Delta ADE \sim \Delta ACB ? Why?

Answer:

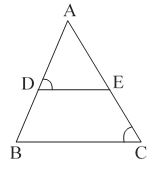
Answer : [True]
In \Delta ADE and \Delta ACB
\angle D=\angle C (given)
\angle A = \angle A (common angle)
And we know that if two angles of one triangle are equal to the two angles of another triangle, then the two triangles are similar by AA similarity criteria.
\therefore \Delta ADE \sim \Delta ACB {by AA similarity criterion}
Hence the given statement is true.

Question:12

Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.

Answer:

Answer. [False]
Given:- (1) An angle of one triangle is equal to an angle of another triangle.
(2) Two sides of one triangle are proportional to the two sides of the other triangle.
According to SAS similarity criterion if one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio, then the triangles are similar.
But here, the given statement is false because one angle and two sides of two triangles are equal but these sides not including equal angle.

NCERT Exemplar Class 10 Maths Solutions Chapter 6: Exercise-6.3

Question:1

In a D PQR, PR2–PQ2 = QR2 and M is a point on side PR such that QM perpendicular to PR.
Prove that : QM2 = PM × MR.
Answer:


Given : PR^{2} - PQ^{2} = QR^{2} \; and\; QM \perp PR
To prove : QM^{2} = PM \times MR
Proof : PR^{2} - PQ^{2} = QR^{2} (given)
PR^{2} = PQ^{2} + QR^{2}
Because \DeltaPQR holds Pythagoras theorem, therefore, \DeltaPQR is right-angled triangle right angle at Q.
In\; \Delta QMR \; and \; \Delta PMQ
\angle M = \angle M {each angle is 90°}
\angle MQR = \angle QPM [each equal to 90° – angle R]
As we know that if the two angles of one triangle are equal to the two angles of another triangle, then the two triangles are similar by AA similarity criterion.
\therefore \Delta QMR \sim \Delta PMQ
Now using the property of area of similar triangles
\frac{ar(\Delta QMR)}{ar(\Delta PMQ)}=\frac{(QM)^{2}}{(PM)^{2}}
\frac{\frac{1}{2}\times RM \times QM}{\frac{1}{2}\times PM \times QM}=\frac{(QM)^{2}}{(PM)^{2}} \left \{ \text {Q area of triangle}=\frac{1}{2}\times base \times height \right \}
\Rightarrow QM^{2} = PM \times RM

Question:2

Find the value of x for which DE || AB in Fig.

Answer:

Answer : [x=2]
Given: DE || AB
According to basic proportionality theorem. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct point, then the other two sides are divided in the same ratio.
\\\therefore \frac{CD}{AD}=\frac{CE}{BE}\\\frac{x+3}{3x+19}=\frac{x}{3x+4}\\\left ( x+3 \right )\left ( 3x+4 \right )=x\left ( 3x+19 \right )
3x^{2}+ 4x + 9x + 12 = 3x^{2} + 19x
19x - 13x = 12
6x = 12
x=\frac{12}{6}=2
Hence the required value of x is 2.

Question:3

In Fig., if angle1 = angle 2 and \Delta NSQ \cong \DeltaMTR, then prove that \DeltaPTS \sim \DeltaPRQ.

Answer:

Given :
\Delta NSQ \cong \Delta MTR \; and\; \angle 1 = \angle 2
To prove:-
\Delta PTS \sim \Delta PRQ
Proof:-
\text {It is given that }\Delta NSQ \cong \Delta MTR
\therefore SQ=TR\; \; \; \; \; ...(1)
\angle 1=\angle 2
We know that sides opposite to equal angles are also equal
\therefore PT=PS \; \; \; \; \; \; \; .....(1)
from equation (1) and (2)
\frac{PS}{SQ}=\frac{PT}{TR}
According to Converse of basic proportionality theorem if a line divides any two sides of a triangle in the same ratio, then the line is parallel to third side.
\therefore ST \parallel QR
\angle 1=\angle PQR \text{(corresponding angle)}
\angle 2=\angle PRQ \text{ (corresponding angle)}
In \Delta PTS and \Delta PRQ
\angle P=\angle P \text{ (corresponding angle)}
\angle 1=\angle PQR
\angle 2=\angle PRQ
We know that if the corresponding angles of two triangles are equal, then the triangles are similar by AAA similarity criterion

\therefore \Delta PTS \sim \Delta PRQ \text{ (by AAA similarity criterion) }

Hence proved

Question:4

Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.

Answer:

Answer: 9:1
Given:- PQRS is a trapezium in which PQ || RS and PQ = 3 RS.
\Rightarrow \frac{PQ}{RS}=\frac{3}{1}

In\; \Delta POQ \; and\; ROS
\angle SOR = \angle QOP (vertically opposite angles)
\angle SRP = \angle RPQ (alternate angle)
As we know that if two angles of one triangle are equal to the two angles of another triangle, then the two triangles are similar by AA similarity criterion
\therefore \Delta POQ\sim \Delta ROS
By the property of area of similar triangle
\frac{ar\left ( \Delta POQ \right )}{ar\left ( \Delta SOR \right )}=\frac{\left ( PQ \right )^{2}}{\left ( RS \right )^{2}}=\left ( \frac{PQ}{RS} \right )^{2}=\left ( \frac{3}{1} \right )^{2}
\frac{ar\left ( \Delta POQ \right )}{ar\left ( \Delta SOR \right )}=\frac{9}{1}
Hence the required ratio is 9: 1.

Question:5

In Fig., if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP.

Answer:

Given:- AB || DC and AC and PQ intersect each other at the point O.
To prove:- OA.CQ = OC.AP
Proof:-
In\; \Delta AOP \; and \; \Delta COQ
\angle AOP = \angle COQ \text{(vertically opposite angles)}
Since AB || OC and PQ is transversal
\therefore \angle APO = \angle CQO \text{(alternate angles)}
As we know that if the two angles of one triangle are equal to the two angles of another triangle, then the two triangles are similar by AA similarity criterion
\therefore \Delta AOP\sim \Delta COQ

Then

\frac{OA}{OC}=\frac{AP}{CQ} \text{[Corresponding sides are proportional]}
By cross multiply we get
OA.CQ = AP.OC
Hence proved.

Question:6

Find the altitude of an equilateral triangle of side 8 cm.

Answer:



Let ABC be an equilateral triangle of side 8 cm
i.e. AB = BC = AC = 8 cm and AD \perp BC
Then D is the mid-point of BC.
\therefore BD=DC=\frac{1}{2}BC=\frac{8}{2}=4cm
Apply Pythagoras theorem in triangle ABD we get
\left ( AB \right )^{2}=\left ( BD \right )^{2}+\left ( AD \right )^{2}
\left ( 8 \right )^{2}=\left ( 4 \right )^{2}+\left ( AD \right )^{2}
64=16+\left ( AD \right )^{2}
64-16=\left ( AD \right )^{2}
48=\left ( AD \right )^{2}
\sqrt{48}=AD
4\sqrt{3}=AD
\text{Hence the altitude of the equilateral triangle is} 4\sqrt{3}cm

Question:7

If \\ \Delta ABC \sim \Delta DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm \; and \; FD = 12 cm, find the perimeter of \Delta ABC.

Answer:

Answer: 18 cm
Given : \Delta ABC \sim \Delta DEF
and AB = 4cm , DE = 6 cm
EF = 9 cm, FD = 12 cm
Here \Delta ABC \sim \Delta DEF (given)
\therefore \frac{AB}{ED}=\frac{BC}{EF}=\frac{AC}{DF}
\frac{4}{6}=\frac{BC}{9}=\frac{AC}{12}
Taking first two terms we get
\frac{4}{6}=\frac{BC}{9}
\frac{9 \times 4}{6}=BC
BC=6 \; cm
Taking first and last terms we get
\frac{4}{6}=\frac{AC}{12}
AC=\frac{4 \times 12}{6}=8
Perimeter \; of\; \Delta ABC = AB + BC + CA
= 4 + 6 + 8 = 18 \; cm.

Question:8

In Fig., if DE || BC, find the ratio of ar (ADE) and ar (DECB).

Answer:

Answer : 1: 3
Given:- DE || BC and DE = 6 cm, BC = 12 cm
In \Delta ABC \; and\; \Delta ADE\angle ABC = \angle ADE \text{ (corresponding angle) }
\angle A = \angle A \text{ (common angle) }
As we know that if two angles of one triangle are equal to the two angles of another triangle, then the two triangles are similar by AA similarity criterion.
\therefore \; \; \; \; \; \Delta ABC \sim \Delta ADE
Then
\frac{ar\left ( \Delta ADE \right )}{ar\left ( \Delta ABC \right )}=\left ( \frac{DE}{BC} \right )^{2}=\left ( \frac{6}{12} \right )^{2}=\left ( \frac{1}{2} \right )^{2}=\frac{1}{4}
Let \; ar\left ( \Delta ADE \right )=\text {k then ar}\left ( \Delta ABC \right )=4k

Now\; ar(\Delta ECB) = ar(\Delta ABC) = ar(\Delta ADE) = 4k - k = 3k

\therefore Required \; ratio = ar(ADE) : ar (DECB)

\\k:3k\\1:3

Question:9

ABCD is a trapezium in which AB ||DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.

Answer:

Answer : [AD=60cm]
Given:- ABCD is a trapezium in which AB || DC, P and Q are points on AD and BC. Such that PQ || DC.
PD = 18 cm, BQ = 35, QC = 15 cm
To prove:- Find AD
Proof:-

Construction:- Join BD
In \Delta ABD, PO || AB
And we know that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then according to basic proportionality theorem the other two sides are divided in the same ratio.
\therefore \frac{DP}{AP}=\frac{DO}{OB}
\Rightarrow \frac{DP}{AP}=\frac{OD}{OB}\; \; \; \; \; \; \; \; \; .....(1)
In \Delta BDC, OQ || DC
Similarly by using basic proportionality theorem.
\frac{BQ}{QC}=\frac{OB}{OD}
\Rightarrow \frac{QC}{BQ}=\frac{OD}{OB}\; \; \; \; \; \; \; \; \; .....(2)
from equation (1) and (2) we get
\frac{DP}{AP}=\frac{QC}{BQ}
\Rightarrow \frac{18}{AP}=\frac{15}{35}
AP=\frac{18 \times 35}{15}
AP=42 \; cm
\\AD = AP + PD\\ 42 + 18 = 60 cm\\ \therefore AD = 60 cm

Question:10

Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.

Answer:

Answer : [108 cm2]
Given:- Corresponding sides of two similar triangles are in the ratio of 2 : 3.
Area of smaller triangle = 48 cm2
We know that the ratio of the areas of two similar triangles is equal to the ratio of the square of any two corresponding sides.
i.e \frac{ar\left ( \text {smaller triangle} \right )}{ar\left ( \text {larger triangle} \right )}=\left ( \frac{2}{3} \right )^{2}
\frac{48}{ar\left ( \text {larger triangle} \right )}=\frac{4}{9}
ar\left ( \text {larger triangle} \right )=\frac{48 \times 9}{4}=12 \times 9=108\; cm^{2}

Question:11

In a triangle PQR, N is a point on PR such that QN \perp PR . If PN. NR = QN2, prove that \angle PQR = 90° .

Answer:

Given:- In a triangle PQR, N is a point on PR such that QN \perp PR and PN.NR = QN2
To prove:-\angle PQR = 90°
Proof:

We have PN.NR = QN2
\\\Rightarrow PN.NR=QN.QN\\\frac{PN}{QN}=\frac{QN}{NR}\; \; \; \; \; \; \; ....(1)
In \Delta QNP \; and\; \Delta RNQ
\frac{PN}{QN}=\frac{QN}{NR}
and \anglePNQ = \angleRNQ (each equal to 90°)
we know that if one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio, then the triangles are similar by SAS similarity criterion.
\therefore \Delta QNP \sim \Delta RNQ
Then \DeltaQNP and \DeltaRNQ are equiangular.
i.e. \angle PQN = \angle QRN \; \; \; \; \; ....(2)
\angle RQN = \angle QPN \; \; \; \; \; ....(3)
adding equation (2) and (3) we get
\angle PQN + \angle RQN = \angle QRN + \angle QPN
\Rightarrow \angle PQR = \angle QRN + \angle QPN \; \; \; \; \; ...(4)
In triangle PQR
\angle PQR + \angle QPR + \angle QRP = 180^{o}
\angle PQR + \angle QPN + \angle QRN = 180^{o}
\begin{Bmatrix} \because \angle QPR=\angle QPN \\\angle QRP=\angle QRN \end{Bmatrix}
\angle PQR + \angle PQR = 180^{o}
[Using equation (4)]
2\angle PQR=180^{o}
\angle PQR=\frac{180^{o}}{2}
\angle PQR=90^{o}
Hence proved

Question:12

Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.

Answer:

Answer : [12 cm ]
Given:- area of smaller triangle = 36 cm2
area of larger triangle = 100 cm2
length of the side of larger triangle = 20 cm
let the length of the corresponding side of the smaller triangle = x cm
According to the property of area of similar triangles,
\frac{ar\left ( \text {larger triangle} \right )}{ar\left ( \text {smaller triangle} \right )}=\frac{\left ( \text {side of larger triangle} \right )^{2}}{\left ( \text {Side of smaller triangle} \right )^{2}}
\frac{100}{36}=\frac{\left ( 20 \right )^{2}}{x^{2}}
x^{2}=\frac{20 \times 20 \times 36}{100}
x=\sqrt{144}
x=12\; cm

Question:13

In Fig., if \angle ACB = \angle CDA, AC = 8 cm and AD = 3 cm, find BD.

Answer:

Answer :
\left [ \frac{55}{3}\; cm\right ]
\text{Given : } \angle ACB=\angle CDA
AC = 8 cm and AD = 3 cm
\text{In} \Delta ACD\; and\; \Delta ABC
\angle A = \angle A
\angle ADC = \angle ACB
We know that if two angles of one triangle are equal to the two angles of another triangle, then the two triangles are similar by AA similarity criterion.
\therefore \; \; \; \; \Delta ADC\sim \Delta ACB
\Rightarrow \frac{AC}{AD}=\frac{AB}{AC} \text{ [corresponding sides are proportional]}
=\frac{8}{3}=\frac{AB}{8}
AB=\frac{8 \times 8}{3}=\frac{64}{3}cm
BD+AD=\frac{64}{3}\; \; \; \; \; \; \; \; \; \; \; \left ( Q\; AB=BD+AD \right )
BD=\frac{64}{3}-AD
BD=\frac{64}{3}-3=\frac{64-9}{3}=\frac{55}{3}\; cm

Question:14

A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.

Answer:

Answer : [10 m]

Let BC = 15 m, AB = 24 m in \DeltaABC and \angleA = Q
Again let DE = 16m and \angleEDF = Q in \DeltaDEF
In \DeltaABC and \DeltaDEF
\angle A=\angle D=Q
\angle B=\angle E=90^{o}
We know that if two angles of one triangle are equal to the two angles of another triangle, then the two triangles are similar by AA similarity criterion.
\therefore \; \; \; \; \; \Delta ABC\sim \Delta DEF
\text{Then }\frac{AB}{DE}=\frac{BC}{EF} \text{(corresponding sides are proportional)}
\frac{24}{16}=\frac{15}{h}
h=\frac{15 \times 16}{24}=10
h=10
Hence the height of the point on the wall where the top of the laden reaches is 10 m.

Question:15

Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.

Answer:

Answer : [8 m]

Here AC = 10 m is a ladder
BC = 6 m distance from the base of the wall.
In right-angle triangle ABC use Pythagoras theorem
\left ( AC \right )^{2}=\left ( AB \right )^{2}+\left ( BC \right )^{2}
\left ( 10 \right )^{2}=\left ( AB \right )^{2}+\left ( 6 \right )^{2}
100= AB^{2}+36
100-36= AB^{2}
64= AB^{2}
AB=\sqrt{64}
AB=8\; m
Hence, the height of the point on the wall where the top of the ladder reaches is 8 m.

NCERT Exemplar Class 10 Maths Solutions Chapter 6: Exercise-6.4

Question:1

\\\text{In Fig., if }\angle A = \angle C, AB = 6 \; cm, BP = 15 \; cm, AP = 12 \; cm \; and \; CP = 4cm
, then find the lengths of PD and CD.

Answer:

Answer: [PD=5cm, CD=2cm]
Given
: \angle A=\angle C,AB=6\; cm,BP=15\; cm
AP = 12 cm and CP = 4 cm
\text{In }\Delta APB\; and\; \Delta CPD
\angle A=\angle C
\angle APB=\angle DPC \text{(Vertically opposite angle) }
\therefore \Delta APB \sim \Delta CPD \text{ [by AA similarity criterion]}
\Rightarrow \frac{AP}{CP}=\frac{PB}{PD}=\frac{AB}{CD}
\frac{12}{4}=\frac{15}{PD}=\frac{6}{CD}
on taking first and second term we get
PD=\frac{15 \times 4}{12}
PD=5\; cm
On taking first and last term we get
\frac{12}{4}=\frac{6}{CD}
CD=\frac{6 \times 4}{12}
CD=2\; cm

Question:2

\text{It is given that } \Delta ABC \sim \Delta EDFsuch that AB = 5 \; cm, AC = 7 \; cm, DF= 15 \; cm and DE = 12 \; cm.
Find the lengths of the remaining sides of the triangles.

Answer:

Answer:
[EF=16.8\; cm, BC= 6.25 \; cm]
Given :
\Delta ABC \sim \Delta EDF
\therefore sides of both triangles are in the same ratio
i.e
\frac{AB}{ED}=\frac{AC}{EF}=\frac{BC}{DF}\; \; \; \; \; \; .....(1)

\text{In } \Delta ABC, AB=5\; cm,AC=7\; cm
\text{In } \Delta DEF, DF=15\; cm,DE=12\; cm
Put all these values in equation (1)
\frac{5}{12}=\frac{7}{EF}=\frac{BC}{15}
Taking the first and second term
\frac{5}{12}=\frac{7}{EF}
EF=\frac{7 \times 12}{5}=\frac{84}{5}=16.8
Taking the first and the last term
\frac{5}{12}=\frac{BC}{15}
BC=\frac{15 \times 5}{12}=\frac{75}{12}=6.25

Question:3

Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.

Answer:


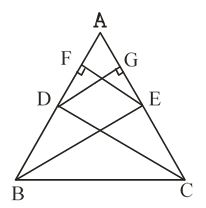
Let ABC is a triangle in which line DE parallel to BC which interest line AB and AC at D and E.
To prove:- line DE divides both sides in the same ratio.
\frac{AD}{DB}=\frac{AE}{EC}
Construction:-
\text{Join BE , CD and draw } EF\perp AB and DG\perp AC
Proof :-
\frac{ar(\Delta ADE)}{ar(\Delta BDE)}=\frac{\frac{1}{2}\times AD \times EF}{\frac{1}{2}\times DB \times EF}
\frac{ar(\Delta ADE)}{ar(\Delta BDE)}=\frac{AD}{DB}\; \; \; \; \; \; \; \; .....(1)
Similarly
\frac{ar(\Delta ADE)}{ar(\Delta DEC)}=\frac{\frac{1}{2}\times AE \times GD}{\frac{1}{2}\times EC \times GD}=\frac{AE}{EC}\; \; \; \; \; \; \; \; ...(2)
Also
ar\left ( \Delta BDE \right )=ar\left ( \Delta DEC \right )\; \; \; \; \; ....(3)
[\Delta BDE\ and \ \Delta DEC\ \text{lie between the same parallel lines DE and BC and on the same base DE ]}
from equation (1), (2) and (3)
\frac{AD}{DB}=\frac{AE}{EC}
Hence proved

Question:4

In Fig, if PQRS is a parallelogram and AB \parallel PS then prove that OC \parallel SR.

Answer:

To prove:-

OC \parallel SR
\text{Proof:- In} \Delta OPS \; and \; \Delta OAB
\angle POS=\angle AOB \text{(common angle)}
\angle OSP=\angle OBA \text{(corresponding angles)}
\therefore \Delta OPS \sim \Delta OAB \text{(by AA similarity criterion)}
\Rightarrow \frac{OS}{OB}=\frac{PS}{AB}\; \; \; \; \; \; \; \; ....(i)
\Rightarrow \frac{QR}{AB}=\frac{CR}{CB}
\frac{PS}{AB}=\frac{CR}{CB}\; \; \; \; \; \; \; \; \; \; ....(2) \left [ \because \; \text {PQRS is parallelogram,}\therefore PS=QR \right ]
from equation (1) and (2)
\frac{OS}{OB}=\frac{CR}{CB}\; or\; \frac{OB}{OS}=\frac{CB}{CR}
Subtracting 1 from both sides
\frac{OB}{OS}-1=\frac{CB}{CR}-1
\frac{OB-OS}{OS}=\frac{CB-CR}{CR}
\frac{BS}{OS}=\frac{BR}{CR}
We know that if a line divides any two sides of a triangle in the same ratio then by converse of basic proportionality theorem the line is parallel to the third side.
\therefore SR\parallel OC
Hence proved.

Question:5

A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.

Answer:

Answer: [0.8 m]

Here, AC = 5m, BC = 4 m, AD = 1.6 m
Let CE = x m
In \Delta ABC use Pythagoras theorem
AC^{2}=AB^{2}+BC^{2}
\left ( 5 \right )^{2}=\left ( AB \right )^{2}+\left ( 4 \right )^{2}
25-16=AB^{2}
9=AB^{2}
AB=\sqrt{9}
AB=3\; m
DB=AB-AD
=3-1.6=1.4\; m
Similarly, in triangle EBD use Pythagoras theorem
ED^{2}=EB^{2}+BD^{2}
\left ( 5 \right )^{2}=EB^{2}+\left ( 1.4 \right )^{2}
23.04=EB^{2}
EB=\sqrt{23.04}
EB=4.8
EB=EB-BC
4.8-4=0.8\; m
Hence the top of the ladder would slide up words on the wall at distance is 0.8 m.

Question:6

For going to a city B from city A, there is a route via city C such that .AC \perp CB, AC = 2 \times km \; and \; CB = 2 (x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.

Answer:

Answer: [8 km]
Given :-
AC \perp CB, AC = 2x\; km, CB = 2 (x + 7) km
AB=26\; km

In \Delta ABC use, Pythagoras theorem
AB^{2}=AC^{2}+BC^{2}
\left ( 26 \right )^{2}=\left ( 2x \right )^{2}+\left ( 2\left ( x+7 \right ) \right )^{2}
676=4x^{2}+4\left ( x^{2}+49+14x \right ) (using \left ( a+b \right )^{2}=a^{2}+b^{2}+2ab)
676=4x^{2}+4x^{2}+196+56x
676=8x^{2}+56x+196
8x^{2}+56x-480=0
Dividing by 8 we get
x^{2}+7x-60=0
x^{2}+12x-5x-60=0
x\left ( x+12 \right )-5\left ( x+12 \right )=0
\left ( x+12 \right )\left ( x-5 \right )=0
x=-12 \; or\; x=5
x = – 12 is not possible because distance cannot be negative.
\therefore x=5
Now
AC = 2x = 2 \times 5 = 10 \; km
BC = 2(x + 7) = 2(5 + 7) = 2 \times 12 = 24 \; km
Distance covered to reach city B from A via city C = AC + CB
=10+24=34\; km
Distance covered to reach city B from city A after the construction of highway
BA = 26\; cm
Saved distance = 34 - 26 = 8 km.

Question:7

A flagpole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.

Answer:

Answer: 20.4 m

height of flag pole BC = 18 m
shadow AB = 9.6 m
In triangle BC using Pythagoras theorem
\\AC^{2}=AB^{2}+BC^{2}\\AC^{2}=\left ( 9.6 \right )^{2}+\left ( 18 \right )^{2}
\\AC^{2}=92.16+324\\AC^{2}=416.16\\AC=\sqrt{416.16}
AC=\sqrt{416.16}=20.4\; m
Hence distance of the top of the pole from the far end of the shadow is 20.4 m

Question:8

A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3m, find how far she is away from the base of the pole.

Answer:

Answer : [9 m]

height of street light bulb = 6 m
woman's height = 1.5 m
woman's shadow = 3m
Let the distance between pole and women = x m
Here\ CD\parallel AB
In\ \Delta CDE and \Delta ABE
\angle E=\angle E \text{(common angle)}
\angle ABE=\angle CDE (\text{ each angle 90}^0)
\therefore \Delta CDE\sim \Delta ABE\text{ (by AA similarity criterion)}
Then
\frac{ED}{EB}=\frac{CD}{AB}
\\\frac{3}{3+x}=\frac{1.5}{6}\\3 \times 6=1.5\left ( 3+x \right )\\18=4.5+1.5x\\18-4.5=1.5x
\\\frac{13.5}{1.5}=x\\9m=x

Question:9

In Fig., ABC is a triangle right angled at B and BD \perp AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.

Answer:

Answer: \left [ 2\sqrt{5}\; cm\; and\; 6\; cm \right ]
Given :- \angle B=90^{o} and BD\perp AC
AD = 4 cm and CD = 5 cm
In \Delta ABD and \Delta BDC
\angle ADB = \angle BDC (each equal to 90o)
\angle BAD = \angle DBC (each equal to 90o-C)
\therefore \Delta ABD\sim \Delta BDC (by AA similarity criterion)
\Rightarrow \frac{DB}{DA}=\frac{DC}{DB}
By cross multiply we get
DB^{2}=DA.DC
DB^{2}=4 \times 5
DB=\sqrt{20}=2\sqrt{5}cm
In \Delta BDC use Pythagoras theorem
BC^{2}=BD^{2}+CD^{2}
BC^{2}=\left ( 2\sqrt{5} \right )^{2}+\left ( 5 \right )^{2}
BC^{2}=20+25=45
BC=\sqrt{45}=3\sqrt{5}
We know that \Delta DBA\sim \Delta DBC
\therefore \frac{DB}{DC}=\frac{BA}{BC}\Rightarrow \frac{2\sqrt{5}}{5}=\frac{BA}{3\sqrt{5}}
BA=\frac{2\sqrt{5}\times 3\sqrt{5}}{5}=\frac{6 \times 5}{5}=6\; cm

Question:10

In Fig., PQR is a right triangle right angled at Q and QS \perp PR . If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.

Answer:

Given: PQR is a triangle

\angle Q = 90^{o} \; and\; QS \perp PR

PQ = 6 cm, PS = 4 cm

In \Delta SQP \; and \; \Delta SRQ

\angle S=\angle S (common angles and each angle is 90°)

\angle SPQ=\angle SQR (each equal to 90^{o}-\angle R)

\therefore \Delta SQP \sim \Delta SRQ ( by AA similarity criterion)

\Rightarrow \frac{SQ}{PS}=\frac{SR}{SQ}
By cross multiply we get
SQ^{2}=PS.SR \; \; \; \; \; \; \; ....(1)
In \Delta PSQ use Pythagoras theorem.
PQ^{2}=PS^{2}+QS^{2}
6^{2}=4^{2}+QS^{2}
36-16=QS^{2}
20=QS^{2}
QS=\sqrt{20}=2\sqrt{5}cm
Put QS=2\sqrt{5} in equation (1)
\left ( 2\sqrt{5} \right )^{2}=4 \times SR
\frac{20}{4}=SR
5cm=SR
In \Delta QSR use Pythagoras theorem
QR^{2}=QS^{2}+SR^{2}
QR^{2}=\left ( 2\sqrt{5} \right )^{2}+\left ( 5 \right )^{2}
QR^{2}=20+25
QR=\sqrt{45}=3\sqrt{5}cm

Question:11

\text{In} \Delta PQR, PD \perp QR \text{such that D lies on QR} . \text{If} PQ = a, PR = b, QD = c \text{and} DR=d\text{, prove that }(a + b) (a - b) = (c + d) (c - d).

Answer:


\text{Given:- PQR is a triangle and} PD\perp QR

PQ = a, PR = b, QD = C, DR = d

To prove:-

(a + b) (a - b) = (c + d) (c - d)
\text{Proof :- In} \Delta PQD \text{use Pythagoras theorem}
\\PQ^{2}=QD^{2}+PD^{2}
\\a^{2}=c^{2}+PD^{2}\\a^{2}-c^{2}=PD^{2} \; \; \; \; \; \; \; \; ....(1)
\text{In } \Delta PRD \text{use Pythagoras theorem }
\\PR^{2}=PD^{2}+DR^{2}\\b^{2}=PD^{2}+d^{2}\\b^{2}-d^{2}=PD^{2}\; \; \; \; \; \; \; ....(2)
equate equation (1) and (2) we get
\\a^{2} - c^{2} = b^{2} - d^{2}\\a^{2}-b^{2}=c^{2}-d^{2}
(a - b) (a + b) = (c - d) (c + d) \left [ \because a^{2} - b^{2} = (a - b) (a + b) \right ]
Hence proved.

Question:12

In a quadrilateral ABCD, \angle A + \angle D = 90^{o}. Prove that AC^{2} + BD^{2} = AD^{2} + BC^{2}

Answer:


Given : ABCD is a quadrilateral, \angle A+\angle D=90^{o}
To prove :- AC^{2} + BD^{2} = AD^{2} + BC^{2}
Proof : In \Delta ADE
\angle A+\angle D=90^{o} \; \; \; \; \; ....(1) (given)
for find \angle E use sum of angle of a triangle is equal to 180°
\angle A+\angle D+\angle E=180^{o}
90+\angle E=180^{o}
\angle E=180^{o} -90^{o}
\angle E=90^{o}
In \Delta ADE use Pythagoras theorem we get
AD^{2}=AE^{2}+DE^{2}\; \; \; \; \; \; \; \; ....(2)
In \Delta BEC use Pythagoras theorem we get
BC^{2}=BE^{2}+EC^{2}\; \; \; \; \; \; \; \; ....(3)
Add equation (2) and (3) we get
AD^{2}+BC^{2}=AE^{2}+DE^{2}+BE^{2}+CE^{2}\; \; \; \; \; \; \; .....(4)
In \Delta ACE use Pythagoras theorem we get
AC^{2}=AE^{2}+CE^{2}\; \; \; \; \; \; \; \; ....(5)
In \Delta EBD use Pythagoras theorem we get
BD^{2}=BE^{2}+DE^{2}\; \; \; \; \; \; \; \; \; \; \; \; ....(6)
Now add equation (5) and (6) we get
AC^{2} + BD^{2} = AE^{2} + CE^{2} + BE^{2} + DE^{2}\; \; \; \; \; \; ....(7)
From equation (4) and (7) we get
AC^{2} + BD^{2} = AD^{2} + BC^{2}
Hence proved.

Question:13

In fig. , l || m and line segments AB, CD and EF are concurrent at point P. Prove tha
t\frac{AE}{BF}=\frac{AC}{BD}=\frac{CE}{FD}.

Answer:

Given: l || m and line segments AB, CD and EF are concurrent at point P
To prove:-
\frac{AE}{BF}=\frac{AC}{BD}=\frac{CE}{FD}
Proof :In \Delta APC \; and\; \Delta DPB
\angle APC=\angle DPB (vertically opposite angles)
\angle PAC=\angle PBD (alternate angles)
and we know that if two angles of one triangle are equal to the two angles of another triangle then the two triangles are similar by AA similarity criterion
\therefore \; \; \; \; \; \Delta APC\sim \Delta DPB
Then, \frac{AP}{BP}=\frac{AC}{BD}=\frac{PC}{PD}\; \; \; \; \; \; \; \; \; ....(1)
In \Delta APE\; and\; \Delta FPB
\angle APE=\angle BPF (vertically opposite angle)
\angle PAE=\angle PBF (alternate angle)
\therefore \; \; \; \; \Delta APE\sim \Delta FPB (by AA similarity criterion)
Then \frac{AP}{PB}=\frac{AE}{BF}=\frac{PE}{PF}\; \; \; \; \; \; \; ...(2)
In \Delta PEC\; and\; \Delta PFD
\angle EPC=\angle FPD (vertically opposite angle)
\angle PCE=\angle PDF (alternate angle)
\therefore \; \; \; \; \Delta PEC\sim \Delta PFD (by AA similarity criterion)
Then \frac{PE}{PF}=\frac{PC}{PD}=\frac{EC}{FD}\; \; \; \; \; \; \; ...(3)
From equation (1), (2) and (3) we get
\frac{AP}{BP}=\frac{AC}{BD}=\frac{AE}{BF}=\frac{PE}{PF}=\frac{EC}{FD}
\Rightarrow \frac{AE}{BF}=\frac{AC}{BD}=\frac{CE}{FD}
Hence proved.

Question:14

In Fig., PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.

Answer:

Answer: \left [ PQ=8_{cm},QR=12\; cm,RS=16\; cm\right ]
Given :- PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm
We know that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
\therefore PA \parallel QB \parallel RC \parallel SD (parallel lines)
Then according to basic proportionality theorem
PQ : QR : RS = AB : BC : CD = 6 : 9 : 12
\text {Let}\\PQ = 6x\\ QR = 9x\\ RS = 12x
length of PS = 36 (given)
\therefore \; \; \; PQ + QR + RS = 36\; \; \; \Rightarrow \; \; \; 6x + 9x + 12x = 36 \; \; \; \; \; \Rightarrow \; \; \; \; \; 27x = 36
x=\frac{36}{27}=\frac{4}{3}
PQ=6x=6 \times\frac{4}{3}=8\; cm
QR=9x=\frac{9\times 4}{3}=12\; cm
RS=12x=\frac{12\times 4}{3}=16\; cm

Question:15

O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.

Answer:

ABCD is a trapezium and O is the point of intersection of the diagonals AC and BD.
AB\parallel DC

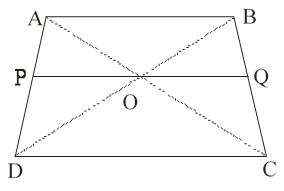
Proof :- \text {In} \Delta ABD \; \text {and }\; \Delta POD
\angle D=\angle D (Common angle)
\angle ABD=\angle POD (corresponding angles)
\therefore \Delta ABD\sim \Delta POD (by AA similarity criterion)
Then \frac{OP}{AB}=\frac{PD}{AD}\; \; \; \; \; \; \; \; \; \; ...(1)
\text {In} \Delta ABC \; \text {and }\; \Delta OQC
\angle C=\angle C (Common angle)
\angle BAC=\angle QOC (corresponding angles)
\therefore \Delta ABC\sim \Delta OQC (by AA similarity criterion)
Then \frac{OQ}{AB}=\frac{QC}{BC}\; \; \; \; \; \; \; \; \; \; ...(2)
\text {In}\Delta ADC
OP\parallel DC
We know that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
\therefore \frac{AP}{PD}=\frac{OA}{OC}\; \; \; \; \; \; \; \; \; ...(3)
\text {Also In}\; \Delta ABC
OQ\parallel AB
\therefore \frac{BQ}{QC}=\frac{OA}{OC}\; \; \; \; \; \; \; \; \; ...(4) (by basic proportionality theorem)
from equation (3) and (4)
\frac{AP}{PD}=\frac{BQ}{QC}
Add 1 on both sides we get
\frac{AP}{PD}+1=\frac{BQ+QC}{QC}
\frac{AP}{PD}=\frac{BC}{QC}
\Rightarrow \frac{PD}{AD}=\frac{QC}{BC}\; \; \; \; \; \; \; ...(5)
\frac{OP}{AB}=\frac{QC}{BC} (use equation (1))
\Rightarrow \frac{OP}{AB}=\frac{OQ}{AB} (use equation (2))
\Rightarrow OP=OQ
Hence proved

Question:16

In Fig., line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and \angle AEF=\angle AFE.Prove that \frac{BD}{CD}=\frac{BF}{CE}.

Answer:

Given: Line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and \angle AEF=\angle AFE
To prove :-
\frac{BD}{CD}=\frac{BF}{CE}
Construction:- Take point G on AB such that CG\parallel DF

Proof:- E is mid-point of CA (given)
\therefore \; \; \; \; \; \; CE = AE
In \Delta ACG, CG\parallel EF and E is mid-point of CA
Then according to mid-point theorem
CE = GF \; \; \; \; \; \; \; ....(1)
In \Delta BCG \; and\; \Delta BDF \; \; CG || DF
According to basic proportionality theorem.
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
\therefore \frac{BC}{CD}=\frac{BG}{GF}
\frac{BC}{CD}=\frac{BF-GF}{GF}
\frac{BC}{CD}=\frac{BF}{GF}=-1
\frac{BC}{CD}+1=\frac{BF}{GF}
\frac{BC}{CD}+1=\frac{BF}{CE} (use equation (1))
\frac{BC+CD}{CD}=\frac{BF}{CE}
\frac{BD}{CD}=\frac{BF}{CE}
Hence proved.

Question:17

Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.

Answer:


Let PQR is a right angle triangle which is right angle at point Q.
PQ = b, QR = a
Three semicircles are drawn on the sides of \Delta PQR having diameters PQ, QR and PR respectively.
Let x_{1}, x_{2} and x_{3} are the areas of semicircles respectively.
To prove:- x_{3}=x_{1}+x_{2}
Proof: In \Delta PQR use Pythagoras theorem we get
PR^{2}=PQ^{2}+QR^{2}
PR^{2}=a^{2}+b^{2}
PR^{2}=\sqrt{a^{2}+b^{2}}
Now area of semi-circle drawn on side PR is
x_{3}=\frac{\pi }{2}\left ( \frac{PR}{2} \right )^{2} \left [ \therefore \text {area of semicircle=}\frac{\pi r^{2}}{2} \right ]
=\frac{\pi}{2}\left ( \frac{\sqrt{a^{2}+b^{2}}}{2} \right )^{2} \left ( \therefore PR=\sqrt{a^{2}+b^{2}} \right )
=\frac{\pi}{2}\times\frac{\left ( a^{2}+b^{2} \right )}{4}
x_{3}=\frac{\pi}{8}\left ( a^{2}+b^{2} \right )
area of semi-circle drawn a side QR is
x_{2}=\frac{\pi }{2}\left ( \frac{QR}{2} \right )^{2}
=\frac{\pi }{2}\left ( \frac{a}{2} \right )^{2}
=\frac{\pi}{2}\times \frac{a^{2}}{4}
x_{2}=\frac{\pi}{8}a^{2}\; \; \; \; \; \; \; ....(2)
area of semicircle drawn on side PQ is
x_{1}=\frac{\pi }{2}\left ( \frac{PQ}{2} \right )^{2}
x_{1}=\frac{\pi }{2}\left ( \frac{b^{2}}{4} \right )\Rightarrow \frac{\pi}{8}b^{2}\; \; \; \; \; \; \; \; ....(3)
add equation (2) and (3) we get
x_{2}+x_{1}=\frac{\pi }{8}a^{2}+\frac{\pi}{8}b^{2}
x_{2}+x_{1}=\frac{\pi }{8}\left ( a^{2}+b^{2} \right )=x_{3}
Hence x_{2}+x_{1}=x_{3}
Hence proved

Question:18

Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.

Answer:


Let PQR is a right angle triangle which is a right angle at point R.
PR = b, RQ = a
Three equilateral triangles are drawn on the sides of triangle PQR that is PRS, RTQ and PUQ
Let x_{1},x_{2} and x_{3} are the areas of equilateral triangles respectively
To prove:- x_{1}+x_{2}=x_{3}
Using Pythagoras theorem in \Delta PQR we get
PQ^{2}+RQ^{2}+RP^{2}
PQ^{2}=a^{2}+b^{2}
PQ=\sqrt{a^{2}+b^{2}}
The formula of area of an equilateral triangle is
=\frac{\sqrt{3}}{4}\left ( side \right )^{2}
\therefore Area of equilateral \Delta RTQ
x_{1}=\frac{\sqrt{3}}{4}\left ( a^{2} \right )\; \; \; \; \; \; \; \; ....(1)
Area of equilateral \Delta RSP
x_{2}=\frac{\sqrt{3}}{4} b^{2} \; \; \; \; \; \; \; \; ....(2)
Area of equilateral \Delta PQU
x_{3}=\frac{\sqrt{3}}{4}\left ( \sqrt{a^{2}+b^{2}} \right )^{2} \left ( Q\; PQ=\sqrt{a^{2}+b^{2}} \right )
x_{3}=\frac{\sqrt{3}}{4} \left ( a^{2}+b^{2} \right )
add equation (1) and (2) we get
x_{1}+x_{2}=\frac{\sqrt{3}}{4}a^{2}+\frac{\sqrt{3}}{4}b^{2}
x_{1}+x_{2}=\frac{\sqrt{3}}{4}\left ( a^{2}+b^{2} \right )=x_{3}
Hence x_{1}+x_{2}=x_{3}
Hence proved

NCERT Exemplar Class 10 Maths Chapter 6 Solutions Important Topics:

  • In this chapter, all the conditions required to prove “any two triangles are similar” is discussed.
  • In this chapter, it is also discussed that if we know the ratio of sides of similar triangles, what relation in their area will be followed.
  • Class 10 Maths NCERT exemplar chapter 6 solutions discusses some triangular theorems such as Pythagoras Theorem.

NCERT Class 10 Exemplar Solutions for Other Subjects:

VMC VIQ Scholarship Test

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Apply
Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

Apply

NCERT Class 10 Maths Exemplar Solutions for Other Chapters:

Features of NCERT Exemplar Class 10 Maths Solutions Chapter 6:

These Class 10 Maths NCERT exemplar chapter 6 solutions provide a detailed knowledge of triangles and the similarity of triangles along with the theorems such as Pythagoras theorem. Most of the question types related to Triangles for Class 10 can be practiced by the students through the exemplar.

The NCERT exemplar Class 10 Maths solutions chapter 6 Triangles, due to its plentiful question bank makes it easier for the student to attempt other books such as NCERT Class 10 Maths, A textbook of Mathematics by Monica Kapoor, RD Sharma Class 10 Maths, RS Aggarwal Class 10 Maths et cetera.

Students get a very resourceful feature of NCERT exemplar Class 10 Maths solutions chapter 6 pdf download through which one can view/download the pdf version of these solutions and use them in case of low/no internet connectivity while practicing NCERT exemplar Class 10 Maths chapter 6 solutions.

Check Chapter-Wise Solutions of Book Questions

Must, Read NCERT Solution Subject Wise

Check NCERT Notes Subject Wise

Also, Check NCERT Books and NCERT Syllabus here

Frequently Asked Questions (FAQs)

1. If two similar triangles have lengths ratio 1:3. What is the ratio of their areas?

We know that if two similar triangles have a sides ratio equal to R then the ratio of their areas will be R2. Therefore, in the given problem the ratio of area of two triangles will be 1:9.

2. What is the condition for two triangles to be similar?

Two triangles are said to be similar if their corresponding angles are equal and the ratio of the corresponding sides is consistent. The basic difference between congruent triangles and similar triangles is that congruent triangles have the same shape and size however similar triangles have different sizes and the same shapes. 

3. Is the chapter Triangles important for Board examinations?

 The chapter Triangles is extremely important for Board examinations as it holds around 10-13% weightage of the whole paper.

4. What type of questions from the chapter Triangles are expected in the board examination?

Generally, the paper consists of 3-4 questions from the chapter of Triangles, and those are mainly distributed between Very Short, Short, and Long Answer questions. NCERT exemplar Class 10 Maths solutions chapter 6 explores all of the above-mentioned type-based questions in detail.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 812 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
IBM
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST
CBSE conducts surprise inspections at 27 schools in Rajasthan, Delhi to curb menace of dummy schools
September 03, 2024 - 03:02 PM IST

Stay up-to date with CBSE Class 10th News

Back to top