NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1 - Coordinate Geometry

Q1 (ii) Find the distance between the following pairs of points : (– 5, 7), (– 1, 3)

Answer:

Given points: (– 5, 7), (– 1, 3)

Distance for the points $(x_{1},y_{1})\ and\ (x_{2},y_{2})$ will be as follows:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

After putting values, we get:

$D= \sqrt{(-1+5)^2+(3-7)^2} = \sqrt{16+16} = 4\sqrt{2}$

Q1 (iii) Find the distance between the following pairs of points :(a, b), (– a, – b)

Answer:

Given points: (a, b), (– a, – b)

Distance for the points $(x_{1},y_{1})\ and\ (x_{2},y_{2})$ will be as follows:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

After putting values, we get:

$D= \sqrt{(-a-a)^2+(-b-b)^2} = \sqrt{4(a^2+b^2)} = 2\sqrt{a^2+b^2}$

Q2 Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2?

Answer:

Given points: (0, 0) and (36, 15)

Distance for the points $(x_{1},y_{1})\ and\ (x_{2},y_{2})$ will be as follows:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

After putting values we get:

$D= \sqrt{(36-0)^2+(15-0)^2} =\sqrt{1296+225} = \sqrt{1521} = 39$

Therefore, the distance between the two towns A and B is, thus, 39 km for the given towns' location $(0,0)$ and $(36,15)$.

Q3 Determine if the points (1, 5), (2, 3), and (– 2, – 11) are collinear.

Answer:

Let the points (1, 5), (2, 3), and (– 2, – 11) represent the vertices A, B, and C of the given triangle, respectively.

$A = (1,5),\ B = (2,3),\ C = (-2,-11)$

To determine whether these points are collinear or not, we need to verify if the sum of the lengths of any two line segments is equal to the length of the third line segment.

Therefore,

$AB = \sqrt{(1-2)^2+(5-3)^2} = \sqrt{5}$

$BC = \sqrt{(2-(-2))^2+(3-(-11))^2} = \sqrt{4^2+14^2} = \sqrt{16+196} = \sqrt{212}$

$CA = \sqrt{(1-(-2))^2+(5-(-11))^2} = \sqrt{3^2+16^2} = \sqrt{9+256} = \sqrt{265}$

$AB+BC \neq CA$

$BA+AC \neq BC$

$BC+CA \neq BA$

Thus, the cases do not satisfy the condition for collinear points

Hence, the points are not collinear.

Q4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.

Answer:

We know the isosceles triangle has two equal sides. So, we will check the distances between the points to verify whether it is an isosceles triangle or not.

The distance between two points $A(x_{1},y_{1})\ and\ B(x_{2},y_{2})$ is given by:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

So, we have the following points: (5, – 2), (6, 4) and (7, – 2), assuming them to be the vertices of triangle A, B, and C, respectively.

$AB = \sqrt{(5-6)^2+(-2-4)^2} = \sqrt{1+36} = \sqrt{37}$

$BC = \sqrt{(6-7)^2+(4+2)^2} = \sqrt{1+36} = \sqrt{37}$

$CA = \sqrt{(5-7)^2+(-2+2)^2} = \sqrt{4+0} = 2$

Therefore, AB = BC

Here two sides are equal in length.

Therefore, ABC is an isosceles triangle.

Q5 In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

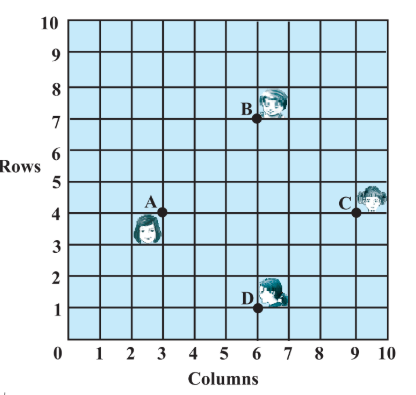
Answer:

The coordinates of the points:

$A(3,4),\ B(6,7),\ C(9,4),\ and\ D(6,1)$ are the positions of 4 friends.

The distance between two points $A(x_{1},y_{1}), \ and\ B(x_{2},y_{2})$ is given by:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

Hence,

$AB = \sqrt{(3-6)^2+(4-7)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2$

$BC = \sqrt{(6-9)^2+(7-4)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2$

$CD = \sqrt{(9-6)^2+(4-1)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2$

$AD= \sqrt{(3-6)^2+(4-1)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2$

And the lengths of diagonals:

$AC = \sqrt{(3-9)^2+(4-4)^2} =\sqrt{36+0} = 6$

$BD = \sqrt{(6-6)^2+(7-1)^2} =\sqrt{36+0} = 6$

So, here it can be seen that all sides of the quadrilateral ABCD are of the same length and the diagonals are also having the same length.

Therefore, quadrilateral ABCD is a square, and Champa is right.

Q6 (i) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)

Answer:

Let the given points $(-1,-2),\ (1,0),\ (-1,2),\ and\ (-3,0)$ represent the vertices A, B, C, and D of the given quadrilateral, respectively.

Apply the distance formula:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

After putting in the values, we get:

$AB= \sqrt{(-1-1)^2+(-2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2$

$BC= \sqrt{(1+1)^2+(0-2)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2$

$CD= \sqrt{(-1+3)^2+(2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2$

$AD= \sqrt{(-1+3)^2+(-2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2$

Finding the length of the diagonals:

$AC= \sqrt{(-1+1)^2+(-2-2)^2} =\sqrt{0+16} = 4$

$BD= \sqrt{(1+3)^2+(0-0)^2} =\sqrt{16+0} = 4$

Thus, it is clear that all sides are of the same length, and also the diagonals have the same length.

Hence, the given quadrilateral is a square.

Q6 (ii) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (–3, 5), (3, 1), (0, 3), (–1, – 4)

Answer:

Let the given points $(-3,5),\ (3,1),\ (0,3),\ and\ (-1,-4)$ represent the vertices A, B, C, and D of the given quadrilateral, respectively.

Apply the distance formula:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

After putting in the values, we get:

$AB= \sqrt{(-3-3)^2+(5-1)^2} =\sqrt{36+16} = \sqrt{52} = 2\sqrt{13}$

$BC= \sqrt{(3-0)^2+(1-3)^2} =\sqrt{9+4} = \sqrt{13}$

$CD= \sqrt{(0+1)^2+(3+4)^2} =\sqrt{1+49} = \sqrt{50} = 5\sqrt2$

$AD= \sqrt{(-3+1)^2+(5+4)^2} =\sqrt{4+81} = \sqrt{85}$

All the sides of the given quadrilateral have different lengths.

Therefore, it is only a general quadrilateral and not a specific one like a square, rectangle, etc.

Q6 (iii) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (4, 5), (7, 6), (4, 3), (1, 2)

Answer:

Let the given points $(4,5),\ (7,6),\ (4,3),\ (1,2)$ represent the vertices A, B, C, and D of the given quadrilateral, respectively.

Apply the distance formula:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

After putting in the values, we get:

$AB= \sqrt{(4-7)^2+(5-6)^2} =\sqrt{9+1} = \sqrt{10}$

$BC= \sqrt{(7-4)^2+(6-3)^2} =\sqrt{9+9} = \sqrt{18}$

$CD= \sqrt{(4-1)^2+(3-2)^2} =\sqrt{9+1} = \sqrt{10}$

$AD= \sqrt{(4-1)^2+(5-2)^2} =\sqrt{9+9} = \sqrt{18}$

And the diagonals:

$AC =\sqrt{(4-4)^2+(5-3)^2} = \sqrt{0+4} = 2$

$BD =\sqrt{(7-1)^2+(6-2)^2} = \sqrt{36+16} = \sqrt{52} = 2\sqrt{13}$

Here we can observe that the opposite sides of this quadrilateral are of the same length.

However, the diagonals are of different lengths.

Therefore, the given points are the vertices of a parallelogram.

Q7 Find the point on the x-axis which is equidistant from (2, -5) and (–2, 9).

Answer:

Let the point which is equidistant from $A(2,-5)\ and \ B(-2,9)$ be $X(x,0)$ as it lies on X-axis.

Then, we have

Distance AX: $= \sqrt{(x-2)^2+(0+5)^2}$ and Distance BX $= \sqrt{(x+2)^2+(0+9)^2}$

According to the question, these distances are of equal length.

Hence, we have,

$\sqrt{(x-2)^2+(0+5)^2}$ $= \sqrt{(x+2)^2+(0+9)^2}$

Solving this to get the required coordinates.

Squaring both sides, we get,

$(x-2)^2+25 = (x+2)^2+81$

$\Rightarrow (x-2+x+2)(x-2-x-2)= 81 - 25 = 56$

$\Rightarrow (-8x)= 56$

Or, $\Rightarrow x = -7$

Hence, the point is $X(-7,0)$.

Q8 Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.

Answer:

Given the distance between the points $P(2,-3)$ and $Q(10,y)$ is 10 units.

The distance formula :

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

So, given $PQ = 10\ units$

$PQ= \sqrt{(10-2)^2+(y-(-3))^2} = 10$

After squaring both sides

$\Rightarrow (10-2)^2+(y-(-3))^2 = 100$

$\Rightarrow (y+3)^2 = 100 - 64$

$\Rightarrow y+3 = \pm 6$

$\Rightarrow y = 6 - 3\ or\ y = -6-3$

Therefore, the values are $y = 3\ or -9$.

Q9 If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also, find the distances QR and PR.

Answer:

Given $Q(0,1)$ is equidistant from $P(5,-3)$ and $R(x,6)$ .

Then, the distances $PQ = RQ$.

Distance $PQ = \sqrt{(5-0)^2+(-3-1)^2} = \sqrt{25+16} = \sqrt{41}$

Distance $RQ = \sqrt{(x-0)^2+(6-1)^2} = \sqrt{x^2+25}$

$\Rightarrow \sqrt{x^2+25} = \sqrt{41}$

Squaring both sides, we get

$\Rightarrow x^2 = 16$

$\Rightarrow x = \pm 4$

The points are: $R(4,6)\ or\ R(-4,6.)$

CASE I: when R is $(4,6)$

The distances QR and PR.

$QR = \sqrt{(0-4)^2+(1-6)^2} = \sqrt{16+25} = \sqrt{41}$

$PR = \sqrt{(5-4)^2+(-3-6)^2} = \sqrt{1^2+(-9)^2} = \sqrt{1+81} = \sqrt{82}$

CASE II: when R is $(-4,6)$

The distances QR and PR.

$QR = \sqrt{(0-(-4))^2+(1-6)^2} = \sqrt{16+25} = \sqrt{41}$

$PR = \sqrt{(5-(-4))^2+(-3-6)^2} = \sqrt{9^2+(-9)^2} = \sqrt{81+81} = 9\sqrt{2}$

Q10 Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4).

Answer:

Let the point $P(x,y )$ is equidistant from $A(3,6)$ and $B(-3,4)$ .

Then, the distances $AP =BP$

$AP = \sqrt{(x-3)^2+(y-6)^2}$ and $BP = \sqrt{(x-(-3))^2+(y-4)^2}$

$\Rightarrow \sqrt{(x-3)^2+(y-6)^2} = \sqrt{(x-(-3))^2+(y-4)^2}$

Squaring both sides: we obtain

$\Rightarrow (x-3)^2+(y-6)^2= (x+3)^2+(y-4)^2$

$\Rightarrow (2x)(-6)+(2y-10)(-2)= 0$ $\left [\because a^2-b^2 = (a+b)(a-b) \right ]$

$\Rightarrow -12x-4y+20 = 0$

$\Rightarrow 3x+y-5 = 0$

Thus, the relation is $3x+y-5 = 0$ between x and y.