NCERT Solutions for Exercise 7.2 Class 10 Maths Chapter 7 - Coordinate Geometry

Q2 Find the coordinates of the points of trisection of the line segment joining (4, –1) and (–2, –3).

Answer:

Let the trisection of the line segment $A(4,-1)$ and $B(-2,-3)$ have the points $P(x_{1},y_{1})$ and $Q(x_{2},y_{2})$

Then,

Section formula: $\left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

By observation point, P divides AB internally in the ratio $1:2$ .

Hence, $m:n = 1:2$

Substituting the values in the equation we get;

$\Rightarrow P\left (\frac{1(-2)+2(4)}{1+2} , \frac{1(-3)+2(-1)}{1+2} \right )$

$\Rightarrow P \left (\frac{-2+8}{3} , \frac{-3-2}{3} \right )$

$\Rightarrow P \left (2 , \frac{-5}{3} \right )$

And by observation point Q, divides AB internally in the ratio $2:1$

Hence, $m:n = 2:1$

Substituting the values in the equation above, we get

$\Rightarrow Q\left (\frac{2(-2)+1(4)}{2+1} , \frac{2(-3)+1(-1)}{2+1} \right )$

$\Rightarrow Q \left (\frac{-4+4}{3} , \frac{-6-1}{3} \right )$

$\Rightarrow Q\left (0 , \frac{-7}{3} \right )$

Hence, the points of trisections are $P \left (2 , \frac{-5}{3} \right )$ and $Q\left (0 , \frac{-7}{3} \right )$

Q3 To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Fig. 7.12. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag

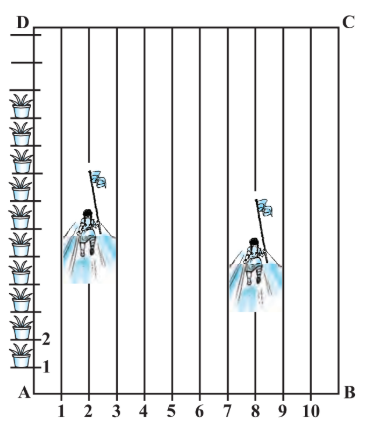
Answer:

Niharika posted the green flag at the distance P, i.e.,

$\frac{1}{4}\times100\ m = 25\ m$ from the starting point of $2^{nd}$ line.

Therefore, the coordinates of this point $P$ are $(2,25).$

Similarly, Preet posted red flag at $\frac{1}{5}$ of the distance Q i.e.,

$\frac{1}{5}\times100\ m = 20\ m$ from the starting point of $8^{th}$ line.

Therefore, the coordinates of this point Q are $(8,20)$ .

The distance $PQ$ is given by,

$PQ = \sqrt{(8-2)^2+(25-20)^2} = \sqrt{36+25} = \sqrt{61} m$

and the point at which Rashmi should post her Blue Flag is the mid-point of the line joining these points. Let this point be $R(x,y)$ .

Then, by Section Formula,

$P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

$x = \frac{2+8}{2},\ y = \frac{25+20}{2}$

$x = 5,\ y = 22.5$

Therefore, Rashmi should post her Blue Flag at 22.5 m on the 5th line.

Q4 Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).

Answer:

Let the ratio be : $k:1$

Then, By section formula:

$P(x,y) = \left (\frac{kx_{2}+x_{1}}{k+1} , \frac{ky_{2}+y_{1}}{k+1} \right )$

Given point $P(x,y) = (-1,6)$

$-1 = \frac{6k-3}{k+1}$

$\Rightarrow -k-1 = 6k-3$

$\Rightarrow k = \frac{7}{2}$

Hence, the point $P$ divides the line AB in the ratio $2:7$ .

Q5 Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.

Answer:

Let the point on the x-axis be $P(x,0)$ and it divides it in the ratio $k:1$ .

Then, we have

Section formula:

$P(x,y) = \left (\frac{kx_{2}+x_{1}}{k+1} , \frac{ky_{2}+y_{1}}{k+1} \right )$

$\implies \frac{ky_{2}+y_{1}}{k+1} = 0$

$k =-\frac{y_{1}}{y_{2}}$

Hence, the value of k will be: $k =-\frac{-5}{5}= 1$

Therefore, the x-axis divides the line in the ratio $1:1$ and the point will be,

Putting the value of $k=1$ in section formula.

$P(x,0) = \left ( \frac{x_{2}+x_{1}}{2}, 0 \right )$

$P(x,0) = \left ( \frac{1-4}{2}, 0 \right ) = \left ( \frac{-3}{2}, 0 \right )$

Q6 If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.

Answer:

Let the given points $A(1,2),\ B(4,y),\ C(x,6),\ D(3,5)$ .

Since the diagonals of a parallelogram bisect each other. Intersection point O of diagonal AC and BD also divides these diagonals.

Therefore, O is the mid-point of AC and BD.

The coordinates of the point O when it is mid-point of AC.

$\left ( \frac{1+x}{2}, \frac{2+6}{2} \right ) \Rightarrow \left ( \frac{x+1}{2}, 4 \right )$

The coordinates of the point O when it is mid-point of BD.

$\left ( \frac{4+3}{2}, \frac{5+y}{2} \right ) \Rightarrow \left ( \frac{7}{2}, \frac{5+y}{2} \right )$

Since both coordinates are of same point O.

Therefore,

$\frac{x+1}{2} =\frac{7}{2}$ and $4 = \frac{5+y}{2}$

Or,

$x = 6\ and\ y = 3$

Q7 Find the coordinates of point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).

Answer:

As the centre point $C(2,-3)$ will be the mid-point of the diameter AB.

Then, the coordinates of point A will be $A(x,y)$ .

Given point $B(1,4)$ .

Therefore,

$(2,-3) = \left ( \frac{x+1}{2}, \frac{y+4}{2} \right )$

$\frac{x+1}{2} = 2\ and\ \frac{y+4}{2} = -3$

$\Rightarrow x = 3\ and\ y = -10$ .

Therefore, the coordinates of A are $(3,-10).$

Q8 If A and B are (- 2, - 2) and (2, - 4), respectively, find the coordinates of P such that AP = 3 AB 7 and P lies on the line segment AB.

Answer:

From the figure:

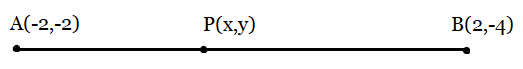
As $AP = \frac{3}{7}AB$

$\Rightarrow PB = \frac{4}{7}AB$ hence the ratio is 3:4,

Now, from the section formula, we can find the coordinates of Point P.

Section Formula:

$P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

$P(x,y)= \left (\frac{3(2)+4(-2)}{3+4} , \frac{3(-4)+4(-2)}{3+4} \right )$

$P(x,y)= \left (\frac{6-8}{7} , \frac{-12-8}{7} \right )$

$P(x,y)= \left (\frac{-2}{7} , \frac{-20}{7} \right )$

Q9 Find the coordinates of the points which divide the line segment joining A (– 2, 2) and B(2, 8) into four equal parts.

Answer:

From the figure:

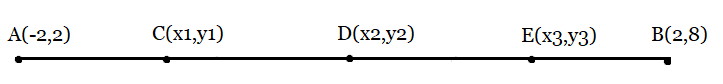
Points C, D, and E divide the line segment AB into four equal parts.

Now, from the section formula, we can find the coordinates of Point C, D, and E.

Section Formula:

$P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

Here point D divides the line segment AB into two equal parts hence

$D(x_{2},y_{2})= \left (\frac{-2+2}{2} , \frac{2+8}{2} \right )$

$D(x_{2},y_{2})= \left (0 , 5 \right )$

Now, point C divides the line segment AD into two equal parts hence

$C(x_{1},y_{1})= \left (\frac{-2+0}{2} , \frac{2+5}{2} \right )$

$C(x_{2},y_{2})= \left (-1 , \frac{7}{2} \right )$

Also, point E divides the line segment DB into two equal parts hence

$E(x_{1},y_{1})= \left (\frac{2+0}{2} , \frac{8+5}{2} \right )$

$E(x_{2},y_{2})= \left (1 , \frac{13}{2} \right )$

Q10 Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order.

Answer:

From the figure:

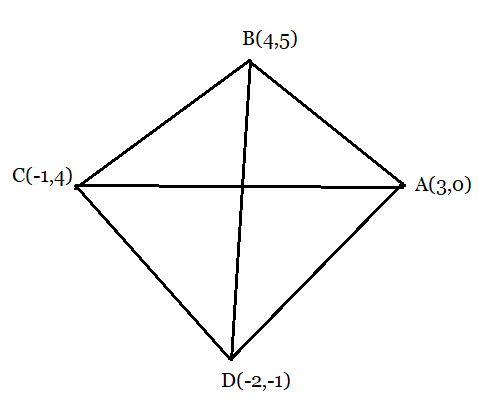
Let the vertices of the rhombus are:

$A(3,0),\ B(4,5),\ C(-1,4),\ D(-2,-1)$

Area of the rhombus ABCD is given by;

$= \frac{1}{2}\times(Product\ of\ lengths\ of\ diagonals)$

Hence we have to find the lengths of the diagonals AC and BD of the rhombus.

The distance formula:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

Length of the diagonal AC:

$AC = \sqrt{(3-(-1))^2+(0-4)^2} = \sqrt{16+16} = 4\sqrt{2}$

Length of the diagonal BD:

$BD = \sqrt{(4-(-2))^2+(5-(-1))^2} = \sqrt{36+36} = 6\sqrt{2}$

Thus, the area will be,

$= \frac{1}{2}\times (AC)\times(BD)$

$= \frac{1}{2}\times (4\sqrt{2})\times(6\sqrt{2}) = 24\ square\ units.$