NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry
Have you ever wondered how engineers design huge buildings, how sailors and pilots navigate through their journey, or how shadows change their length throughout the day? All of these answers can be found in Trigonometry, a fascinating branch of mathematics. As per the latest syllabus, this chapter contains the basic concepts of trigonometry, like trigonometric ratios, trigonometric identities, trigonometric ratios of some specific angles, and trigonometric ratios of complementary angles. NCERT Solutions for Class 10 can help the students understand these concepts and will make them more efficient in solving problems involving height, distance, and angles.
This Story also Contains
- NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry: Download Free PDF
- NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry (Exercises)
- Introduction to Trigonometry Class 10 NCERT solutions: Exercise-wise
- Class 10 Maths NCERT Chapter 8: Extra Question
- Introduction to Trigonometry Class 10 Chapter 8: Topics
- Introduction to Trigonometry Class 10 NCERT Solutions - Important Formulae
- Why are Class 10 Maths Chapter 8 Introduction to Trigonometry question answers important?
- NCERT Solutions for Class 10 Maths: Chapter Wise
These NCERT Solutions for class 10 Maths are designed by our experienced subject experts at Careers360 to offer clear and step-by-step solutions for the exercise problems and help students to prepare well for exams and to gain knowledge about all the natural processes happening around them through a series of solved questions. It covers questions from all the topics and will help you improve your speed and accuracy. Many teachers recommend NCERT Solutions because they closely match the exam pattern. Check this NCERT article for complete syllabus coverage along with NCERT Books, Solutions, Syllabus, and Exemplar Problems with Solutions.
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry: Download Free PDF
Careers360 brings you NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry (Exercises)
Here are the NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry question answers with clear, detailed solutions.
| Introduction to Trigonometry Class 10 Question Answers Exercise: 8.1 Page number: 121 Total questions: 11 |
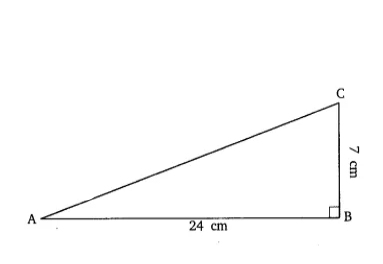
Q1. In $\Delta \: ABC$ , right-angled at $B, AB = 24 \: cm$ , $BC = 7 \: cm$.
Determine : $(i)\; \sin A, \cos A$ $(ii)\; \sin C, \cos C$
Answer:
We have,
In $\Delta \: ABC$ , $\angle$B = 90, and the length of the base (AB) = 24 cm and length of perpendicular (BC) = 7 cm
So, by using Pythagoras' theorem,
$AC^2 = AB^2 + BC^2$
⇒ $AC = \sqrt{AB^2+BC^2}$
⇒ $AC = \sqrt{576+49}$
⇒ $AC = \sqrt{625}$
⇒ $AC = 25$ cm
Now,
(i) $\sin A = \frac{P}{H} = \frac{BC}{AC} = \frac{7}{25}$
$\cos A = \frac{B}{H} = \frac{BA}{AC} = \frac{24}{25}$
(ii) For angle C, AB is perpendicular to the base (BC).
Here, B indicates Base and P means perpendicular wrt angle $\angle$C
So, $\sin C = \frac{P}{H} = \frac{BA}{AC} = \frac{24}{25}$
and $\cos C = \frac{B}{H} = \frac{BC}{AC} = \frac{7}{25}$
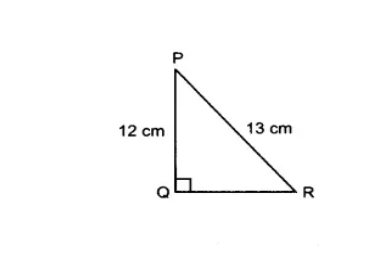
Q2. In Fig. 8.13, find $\tan P - \cot R$ .
Answer:
We have $\Delta$PQR
According to Pythagoras, in a right-angled triangle, the lengths of PQ and PR are 12 cm and 13 cm, respectively.
So, by using Pythagoras' theorem,
$QR = \sqrt{13^2-12^2}$
$QR = \sqrt{169-144}$
$QR = \sqrt{25} = 5\ cm$
Now, according to the question,
$\tan P -\cot R$ = $\frac{RQ}{QP}-\frac{QR}{PQ} = \frac{5}{12} - \frac{5}{12} = 0$
Q3. If $\sin A=\frac{3}{4},$ calculate $\cos A$ and $\tan A$ .
Answer:
Suppose $\Delta$ ABC is a right-angled triangle in which $\angle B = 90°$ and we have $\sin A=\frac{3}{4},$
So,
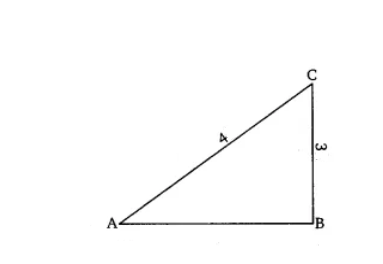
Let the length of AB be 4 units and the length of BC = 3 units. So, by using Pythagoras' theorem,
$AB = \sqrt{16-9} = \sqrt{7}$ units
Therefore,
$\cos A = \frac{AB}{AC} = \frac{\sqrt{7}}{4}$ and $\tan A = \frac{BC}{AB} = \frac{3}{\sqrt{7}}$
Q4. Given $15 \cot A=8,$ find $\sin A$ and $\sec A$ .
Answer:
We have,
$15 \cot A=8$ $\Rightarrow \cot A =\frac{8}{15}$
It implies that in the triangle ABC, in which $\angle B =90°$. The length of AB is 8 units, and the length of BC = 15 units
Now, by using Pythagoras' theorem,
$AC = \sqrt{64 +225} = \sqrt{289}$
$\Rightarrow AC =17$ units
So, $\sin A = \frac{BC}{AC} = \frac{15}{17}$
and $\sec A = \frac{AC}{AB} = \frac{17}{8}$
Q5. Given $\sec \theta =\frac{13}{12},$ calculate all other trigonometric ratios.
Answer:
We have,
$\sec \theta =\frac{13}{12},$
This means that the hypotenuse of the triangle is 13 units, and the base is 12 units.
Let ABC be a right-angled triangle in which $\angle$ B is 90 and AB is the base, BC is the perpendicular height, and AC is the hypotenuse.
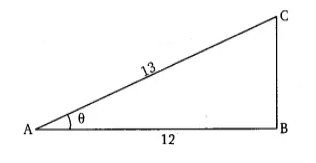
By using Pythagoras' theorem,
$BC = \sqrt{169-144}=\sqrt{25}$
$\Rightarrow BC = 5$ units
Therefore,
$\sin \theta = \frac{BC}{AC}=\frac{5}{13}$
$\cos \theta = \frac{BA}{AC}=\frac{12}{13}$
$\tan \theta = \frac{BC}{AB}=\frac{5}{12}$
$\cot \theta = \frac{BA}{BC}=\frac{12}{5}$
$\sec \theta = \frac{AC}{AB}=\frac{13}{12}$
$\csc \theta = \frac{AC}{BC}=\frac{13}{5}$
Answer:
We have A and B are two acute angles of triangle ABC, and $\cos A =\cos B$.

According to the question, in triangle ABC,
$\cos A =\cos B$
$\frac{AC}{AB}=\frac{BC}{AB}$
$\Rightarrow AC = AB$
Therefore, $\angle$ A = $\angle$ B [angles opposite to equal sides are equal]
Q7. If $\cot \theta =\frac{7}{8},$ evaluate: $(i)\; \frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}$ $(ii)\; \cot ^{2}\theta$
Answer:
Given that,
$\cot \theta =\frac{7}{8}$
$\therefore$ perpendicular (AB) = 8 units and Base (BC) = 7 units
Draw a right-angled triangle ABC in which $\angle B =90°$
Now, by using Pythagoras' theorem,
$AC^2 = AB^2+BC^2$
$AC = \sqrt{64 +49} =\sqrt{113}$
So, $\sin \theta = \frac{AB}{AC} = \frac{8}{\sqrt{113}}$
and $\cos \theta = \frac{BC}{AC} = \frac{7}{\sqrt{113}}$
$\Rightarrow \cot \theta =\frac{\cos \theta}{\sin \theta} = \frac{7}{8}$
$(i)\; \frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}$
$\Rightarrow \frac{(1-\sin^2\theta)}{(1-\cos^2\theta)} = \frac{\cos^2\theta}{\sin^2\theta} = \cot ^2\theta=(\frac{7}{8})^2 = \frac{49}{64}$
$(ii)\; \cot ^{2}\theta$
$=(\frac{7}{8})^2 = \frac{49}{64}$
Q8. If $3\cot A=4,$ check wether $\frac{1-\tan ^{2}A}{1+\tan ^{2}A}=\cos ^{2}A-\sin ^{2}A$ or not.
Answer:
Given that,
$3\cot A=4,$
$\Rightarrow \cot A= \frac{4}{3} = \frac{base}{perp.}$
ABC is a right-angled triangle in which $\angle B =90°$, and the length of the base AB is 4 units, and the length of the perpendicular is 3 units
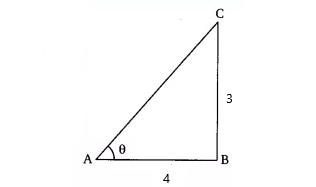
By using Pythagoras' theorem, in triangle ABC,
$\\AC^2=AB^2+BC^2\Rightarrow AC = \sqrt{16+9}\Rightarrow AC = \sqrt{25}$
$\Rightarrow AC = 5$ units
So,
$\tan A = \frac{BC}{AB} = \frac{3}{4}$
$\cos A = \frac{AB}{AC} = \frac{4}{5}$
$\sin A = \frac{BC}{AC} = \frac{3}{5}$
$\frac{1-\tan ^{2}A}{1+\tan ^{2}A}=\cos ^{2}A-\sin ^{2}A$
Putting the values of the above trigonometric ratios, we get;
$\Rightarrow \frac{1-\frac{9}{16}}{1+\frac{9}{16}} = \frac{16}{25}-\frac{9}{25}$
$\Rightarrow \frac{7}{25} = \frac{7}{25}$
LHS $=$ RHS
Q9. In triangle $ABC$ , right-angled at $B$ , if $\tan A =\frac{1}{\sqrt{3}},$ find the value of:
$(i) \sin A\: \cos C + \cos A\: \sin C$
$(ii) \cos A\: \cos C + \sin A\: \sin C$
Answer:
Given a triangle ABC, right-angled at B and $\tan A =\frac{1}{\sqrt{3}}$ $\Rightarrow A=30°$

According to question, $\tan A =\frac{1}{\sqrt{3}} = \frac{BC}{AB}$
By using Pythagoras' theorem,
$\\AC^2 = AB^2+BC^2\Rightarrow AC = \sqrt{1+3} =\sqrt{4}$
$\Rightarrow AC = 2$
Now,
$\\\sin A = \frac{BC}{AC} = \frac{1}{2}, \sin C =\frac{AB}{AC} = \frac{\sqrt{3}}{2}, \cos A = \frac{AB}{AC} = \frac{\sqrt{3}}{2}, \cos C = \frac{BC}{AC} = \frac{1}{2}$
Therefore,
$(i) \sin A\: \cos C + \cos A\: \sin C$
$= \frac{1}{2}\times\frac{1}{2}+\frac{\sqrt{3}}{2}\times \frac{\sqrt{3}}{2}=\frac{1}{4} +\frac{3}{4} = 1$
$(ii) \cos A\: \cos C + \sin A\: \sin C$
$= \frac{\sqrt{3}}{2}\times \frac{1}{2}+\frac{1}{2}\times\frac{\sqrt{3}}{2}= \frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}= \frac{\sqrt{3}}{2}$
Answer:

We have, PR + QR = 25 cm.............(i)
PQ = 5 cm and $\angle Q =90°$
According to the question,
In triangle $\Delta$ PQR,
By using Pythagoras' theorem,
$PR^2 = PQ^2+QR^2$
$\Rightarrow PQ^2 =PR^2-QR^2$
$\Rightarrow 5^2= (PR-QR)(PR+QR)$
$\Rightarrow 25 = 25(PR-QR)$
$\Rightarrow PR - QR = 1$........(ii)
From equation(i) and equation(ii), we get;
PR = 13 cm and QR = 12 cm.
Therefore,
$\sin P= \frac{QR}{PR}= \frac{12}{13}$
$\cos P = \frac{PQ}{RP} = \frac{5}{13}$
$\tan P = \frac{\sin P}{\cos P} = \frac{12}{5}$
Q11. State whether the following are true or false. Justify your answer.
(i) The value of $\tan A$ is always less than 1.
(ii) $\sec A=\frac{12}{5}$ for some value of angle A.
(iii) $\cos A$ is the abbreviation used for the cosecant of angle A.
(iv) $\cot A$ is the product of cot and A.
(v) $\sin \theta =\frac{4}{3}$ for some angle $\theta .$
Answer:
(i) False,
because $\tan 60 = \sqrt{3}$ , which is greater than 1
(ii) True,
because $\sec A \geq 1$
(iii) False,
Because the $\cos A$ abbreviation is used for cosine A.
(iv) False,
because the term $\cot A$ is a single term, not a product.
(v) False,
because $\sin \theta$ lies between (-1 to +1) [ $-1\leq \sin \theta\leq 1$]
| Introduction to Trigonometry Class 10 Question Answers Exercise: 8.2 Page number: 127 Total questions: 4 |
$(i) \sin 60°\cos 30°+\sin30° \cos 60°$
Answer:
As we know,
the value of $\sin 60° = \frac{\sqrt{3}}{2} = \cos 30°$ , $\sin 30° = \frac{1}{2}=\cos 60°$
$\sin 60°\cos 30°+\sin30° \cos 60°$
$= \frac{\sqrt{3}}{2}.\frac{\sqrt{3}}{2}+ \frac{1}{2}.\frac{1}{2}\\$
$=\frac{3}{4}+\frac{1}{4}$
$=1$
$(ii)\: 2\tan ^{2}45°+ 2\cos ^{2}30°- 2\sin ^{2}60°$
Answer:
We know the value of
$\tan 45°= 1$ and
$\cos 30° = \sin 60° = \frac{\sqrt{3}}{2}$
According to the question,
$=2\tan ^{2}45°+ 2\cos ^{2}30°- 2\sin ^{2}60°$
$\\=2(1)^2+ 2(\frac{\sqrt{3}}{2})^2-2(\frac{\sqrt{3}}{2})^2\\=2$
$(iii)\: \frac{\cos 45^{\circ}}{\sec 30^{\circ}+\operatorname{cosec} 30^{\circ}}$
Answer:
$\frac{\cos 45^{\circ}}{\sec 30^{\circ}+\operatorname{cosec} 30^{\circ}}$
We know the value of
$\cos 45^{\circ} = \frac{1}{\sqrt{2}}$ , $\sec 30^{\circ}= \frac{2}{\sqrt {3}}$ and $\operatorname{cosec}30^{\circ} =2$ ,
After putting these values
$=\frac{\frac{1}{\sqrt{2}}}{\frac{2}{\sqrt{3}}+2}$
$=\frac{\frac{1}{\sqrt{2}}}{\frac{(2+2\sqrt{3})}{ \sqrt{3}}}$
$\\=\frac{\sqrt{3}}{2\sqrt{2}+2\sqrt{6}}\times\frac{2\sqrt{2}-2\sqrt{6}}{2\sqrt{2}-2\sqrt{6}}$
$\\=\frac{2\sqrt{6}-2\sqrt{18}}{-16}\\ =2(\frac{\sqrt{6}-3\sqrt{3}}{-16}) = \frac{3\sqrt{3}-\sqrt{6}}{8}$
$(iv)\: \frac{\sin 30°+\tan 45°-\operatorname{cosec} 60°}{\sec 30°+\cos 60°+\cot 45°}$
Answer:
$\frac{\sin 30°+\tan 45°-\operatorname{cosec} 60°}{\sec 30°+\cos 60°+\cot 45°}$ ..................(i)
It is known that the values of the given trigonometric functions,
$\\\sin 30° = \frac{1}{2}=cos 60°, \tan 45° = 1=\cot 45°, \sec 30° = \frac{2}{\sqrt{3}}=\operatorname{cosec} 60°$
Putting all these values in equation (i), we get;
$\\\Rightarrow \frac{\frac{1}{2}+1-\frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}}+\frac{1}{2}+1}=\frac{\frac{3}{2}-\frac{2}{\sqrt{3}}}{\frac{3}{2}+\frac{2}{\sqrt{3}}}= \frac{3\sqrt{3}-4}{3\sqrt{3}+4}\times\frac{4-3\sqrt{3}}{4-3\sqrt{3}}= \frac{12\sqrt{3}-27-16+12\sqrt{3}}{-11}= \frac{43-24\sqrt{3}}{11}$
$(v)\frac{5\cos^{2}60°+ 4\sec^{2}30°-\tan^{2}45°}{\sin^{2}30°+\cos^{2}30°}$
Answer:
$\frac{5\cos^{2}60°+ 4\sec^{2}30°-\tan^{2}45°}{\sin^{2}30°+\cos^{2}30°}$ .....................(i)
We know the values of,
$\\\cos 60° = \frac{1}{2}= \sin 30°, \sec 30° = \frac{2}{\sqrt{3}}, \tan 45° = 1, \cos 30° = \frac{\sqrt{3}}{2}$
By substituting all these values in equation(i), we get;
$\\\Rightarrow \frac{5.(\frac{1}{2})^2+4.(\frac{2}{\sqrt{3}}) ^2-1}{(\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}= \frac{\frac{5}{4}-1+\frac{16}{3}}{1}= \frac{\frac{1}{4}+\frac{16}{3}}{1}=\frac{67}{12}$
Q2. Choose the correct option and justify your choice :
$(i)\, \frac{2\: \tan 30°}{1+\tan ^{2}30°}=$
$(A)\: \sin 60°$ $(B)\: \cos 60°$ $(C)\: \tan 60°$ $(D)\: \sin 30°$
Answer:
Put the value of $\tan 30°$ in the given question-
$\frac{2\: \tan 30°}{1+\tan ^{2}30°}=\frac{2\times\frac{1}{\sqrt{3}}}{1+(\frac{1}{\sqrt{3}})^2}=\frac{2}{\sqrt{3}}\times \frac{3}{4}=\frac{\sqrt{3}}{2} = \sin 60°$
The correct option is (A).
Q2. Choose the correct option and justify your choice :
$(ii)\: \frac{1-\tan^{2}45°}{1+ \tan^{2}45°}=$
$(A)\: \tan \: 90°$ $(B)\: 1$ $(C) \: \sin 45°$ $(D) \: 0$
Answer:
$\frac{1-\tan^{2}45°}{1+ \tan^{2}45°}=$
We know that $\tan 45° = 1$
So, $\frac{1-1}{1+1}=0$
The correct option is (D).
Q2. Choose the correct option and justify your choice :
$(iii)\sin \: 2A=2\: \sin A$ is true when $A$ =
$(A)0°$ $(B)\: 30°$ $(C)\: 45°$ $(D)\: 60°$
Answer:
The correct option is (A).
$\sin \: 2A=2\: \sin A$
We know that $\sin 2A = 2\sin A \cos A$
So, $2\sin A \cos A = 2\sin A$
$\\\cos A = 1, A = 0°$
Q2. Choose the correct option and justify your choice :
$(iv)\frac{2\: \tan 30°}{1-tan^{2}\: 30°}=$
$(A)\: \cos 60°$ $(B)\: \sin 60°$ $(C)\: \tan 60°$ $(D)\: \sin 30°$
Answer:
Put the value of $tan 30°={\frac{1}{\sqrt{3}}}$
$\\=\frac{2\: \tan 30°}{1-tan^{2}\: 30°}=\frac{2\times \frac{1}{\sqrt{3}}}{1-(\frac{1}{\sqrt{3}})^2}\\ =\frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}}\\ =\frac{2}{\sqrt{3}}\times \frac{3}{2}\\ =\sqrt{3}= \tan 60°$
The correct option is (C).
Answer:
Given that,
$\tan (A+B) = \sqrt{3} =\tan 60°$
So, $A + B = 60°$ ..........(i)
$\tan (A-B) = \frac{1}{\sqrt{3}} =\tan 30°$
therefore, $A - B = 30°$ .......(ii)
By solving equations (i) and (ii), we get;
$A = 45°$ and $B = 15°$
Q4. State whether the following are true or false. Justify your answer.
$(i) \sin (A + B) = \sin A + \sin B$
$(ii)$ The value of $\sin \theta$ increases as $\theta$ increases.
$(iii)$ The value of $\cos \theta$ increases as $\theta$ increases.
$(iv)\sin \theta =\cos \theta$ for all values of $\theta$ .
$(v) \cot A$ is not defined for $A=0°$
Answer:
(i) False,
Let A = B = $45°$
Then, $\\\sin(45°+45°) = \sin 45°+\sin 45°$
$\sin 90° = \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}} \neq 1$
(ii) True,
Take $\theta = 0°,\ 30°,\ 45°$
when
$\theta$ = 0 then zero(0),
$\theta$ = 30 then value of $\sin \theta$ is $\frac{1}{2}$ = 0.5
$\theta$ = 45 then value of $\sin \theta$ is $\frac{1}{\sqrt2}$ = 0.707
(iii) False,
$\cos 0° = 1,\ \cos 30° = \frac{\sqrt{3}}{2}= 0.87,\ \cos 45° = \frac{1}{\sqrt2}= 0.707$
(iv) False,
Let $\theta = 0°$
$\\\sin 0° = 0$ and $\cos 0°=1$
(v) True,
$\cot 0° = \frac{\cos 0°}{\sin 0°}=\frac{1}{0}$ (not defined).
|
Introduction to Trigonometry Class 10 Question Answers |
Q1. Express the trigonometric ratios $\sin A,\sec, and \tan A$ in terms of $\cot A$.
Answer:
We know that $\csc^2A -\cot^2A = 1$
(i)
$\\\Rightarrow \frac{1}{\sin^2A}= 1+\cot^2A\\ \Rightarrow\sin^2A = \frac{1}{1+\cot^2A}\\ \Rightarrow \sin A = \frac{1}{\sqrt{1+\cot^2A}}$
(ii) We know the identity of
$\sec ^2 A-\tan ^2 A=1$
$\Rightarrow \sec^2 A=1+\frac{1}{\cot^2\theta}$
$\Rightarrow \sec A=\frac{\sqrt{\cot^2\theta+1}}{\cot\theta}$
(iii) $\tan A = \frac{1}{\cot A}$
Q2. Write all the other trigonometric ratios of $\angle A$ in terms of $\sec A$.
Answer:
We know that the identity $\sin^2 A + \cos^2 =1$
$\\\sin^2 A =1- \cos^2 A$
$\sin^2A = 1-\frac{1}{\sec^2A}=\frac{\sec^2A -1}{\sec^2A}$
$\sin A =\sqrt{\frac{\sec^2A -1}{\sec^2A}}=\frac{{}\sqrt{\sec^2A -1}}{\sec A}$
$cosec A =\frac{\sec A}{\sqrt{\sec^2A -1}}$
$\tan A = \frac{\sin A}{\cos A} = \sqrt{\sec^2A -1}$
$\cot A =\frac{1}{ \sqrt{\sec^2A -1}}$
$\cos A=\frac{1}{\sec A}$
Q3. Choose the correct option. Justify your choice.
$(i) 9\sec^{2}A-9\tan^{2}A=$
(A) 1 (B) 9 (C) 8 (D) 0
Answer:
The correct option is (B) = 9
$9\sec^2A-9 \tan ^2A = 9(\sec^2A- \tan ^2A)$ .............(i)
And it is known that sec2A - tan2A = 1
Therefore, equation (i) becomes, $9\times 1 = 9$
Q3. Choose the correct option. Justify your choice.
$(ii)(1+\tan \theta +\sec \theta )(1+\cot \theta -cosec\: \theta )=$
(A) 0 (B) 1 (C) 2 (D) –1
Answer:
The correct option is (C)
$(1+\tan \theta +\sec \theta )(1+\cot \theta -cosec\: \theta )$ .......................(i)
We can write the above equation as;
$=(1+\frac{\sin \theta}{\cos \theta} +\frac{1}{\cos \theta})(1+\frac{\cos\theta}{\sin \theta} -\frac{1}{sin\theta})$
$= \frac{(1+\sin\theta+\cos\theta)}{\cos\theta.\sin\theta}\times (\frac{(\sin\theta+\cos\theta-1}{\sin\theta.\cos\theta})$
$= \frac{(\sin\theta+\cos\theta)^2-1^2}{\sin\theta.\cos\theta}$
$= \frac{\sin^2\theta+\cos^2\theta+2\sin\theta.\\cos\theta-1}{\sin\theta.\cos\theta}$
$= 2\times\frac{\sin\theta.\cos\theta}{\sin\theta.\cos\theta}$
$= 2$
Q3. Choose the correct option. Justify your choice.
$(iii) (\sec A+\tan A)(1-\sin A)=$
$(A)\sec A$ $(B)\sin A$ $(C)cosec A$ $(D) \cos A$
Answer:
The correct option is (D)
$(\sec A+\tan A)(1-\sin A)$
$= ( \frac{1}{\cos A}+\frac{\sin A}{\cos A})(1-\sin A)= \frac{1+\sin A}{\cos A}(1-\sin A)= \frac{1-\sin^2 A}{\cos A}= \cos A$
Q3. Choose the correct option. Justify your choice.
$(iv) \frac{1+\tan ^{2}A}{1+\cot ^{2}A}=$
$(A) \sec ^{2}A$ $(B) -1$ $(C) \cot ^{2}A$ $(D) \tan ^{2}A$
Answer:
The correct option is (D)
$\frac{1+\tan ^{2}A}{1+\cot ^{2}A}$
We know that $\cot A = \frac{1}{\tan A}$
therefore,
$\\\Rightarrow \frac{1+\tan ^{2}A}{1+\frac{1}{\tan ^{2}A}}= \tan^2A\times(\frac{1+\tan^2 A}{1+\tan^2A})= \tan^2A$
$(i) (\csc \theta -\cot \theta )^{2}= \frac{1-\cos \theta }{1+\cos \theta }$
Answer:
We need to prove-
$(\csc \theta -\cot \theta )^{2}= \frac{1-\cos \theta }{1+\cos \theta }$
Now, taking LHS,
$(\csc\theta-\cot\theta)^2 = (\frac{1}{\sin\theta}-\frac{\cos\theta}{\sin\theta})^2$
$\\= (\frac{1-\cos\theta}{\sin\theta})^2\\ =\frac{(1-\cos\theta)(1-\cos\theta)}{\sin^2\theta}\\$
$\\=\frac{(1-\cos\theta)(1-\cos\theta)}{1-\cos^2\theta}\\\\ =\frac{(1-\cos\theta)(1-\cos\theta)}{(1-\cos\theta)(1+\cos\theta)}\\\\ =\frac{1-\cos\theta}{1+\cos\theta}$
LHS = RHS
Hence proved.
$(ii) \frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}= 2\sec A$
Answer:
We need to prove-
$\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}= 2\sec A$
Taking LHS;
$\\=\frac{\cos^2A+1+\sin^2A+2\sin A}{\cos A(1+\sin A)}\\\\ =\frac{2(1+\sin A)}{\cos A(1+\sin A)}\\\\ =\frac{2}{\cos A} = 2\sec A$
= RHS
Hence proved.
$(iii)\frac{\tan \theta }{1-\cot \theta }+\frac{\cot \theta }{1-\tan \theta }=1+\sec \theta \csc \theta$
[ Hint: Write the expression in terms of $\sin \theta$ and $\cos\theta$ ]
Answer:
We need to prove-
$\frac{\tan \theta }{1-\cot \theta }+\frac{\cot \theta }{1-\tan \theta }=1+\sec \theta \:cosec \theta$
Taking LHS;
$\\\Rightarrow \frac{\tan^2 \theta }{\tan \theta-1 }+\frac{1}{\tan\theta(1-\tan \theta)}=\frac{\tan^3\theta-\tan^4\theta+\tan\theta-1}{(\tan\theta-1).\tan\theta.(1-\tan\theta)}= \frac{(\tan^3\theta-1)(1-\tan\theta)}{\tan\theta.(\tan\theta-1)(1-\tan\theta)}\\$
By using the identity $a^3-b^3=(a-b)(a^2+ab+b^2)$
$\\\Rightarrow \frac{(\tan\theta -1)(\tan^2\theta+1+\tan\theta)}{\tan\theta(\tan\theta -1)}= \tan\theta+1+\frac{1}{\tan\theta}= 1+\frac{1+\tan^2\theta}{\tan\theta}= 1+\sec^2\theta \times \frac{1}{\tan\theta}= 1+\sec\theta.\csc\theta\\\\ =RHS$
Hence proved.
$(iv)\frac{1+\sec A}{\sec A}=\frac{\sin ^{2}A}{1-\cos A}$
[ Hint: Simplify LHS and RHS separately.]
Answer:
We need to prove-
$\frac{1+\sec A}{\sec A}=\frac{\sin ^{2}A}{1-\cos A}$
Taking LHS;
$\\\Rightarrow \frac{1+\sec A}{\sec A}= \frac{(1+\frac{1}{\cos A})}{\sec A}= 1+\cos A$
Taking RHS;
We know that identity $1-\cos^2\theta = \sin^2\theta$
$\\\Rightarrow \frac{\sin ^{2}A}{1-\cos A}= \frac{1-\cos^2 A}{1-\cos A}= \frac{(1-\cos A)(1+\cos A)}{(1-\cos A)}= 1+\cos A$
LHS = RHS
Hence proved.
Q4. Prove the following identities, where the angles involved are acute angles for which the expressions are defined. $(v) \frac{\cos A-\sin A+1}{\cos A+\sin A-1}= \csc A+\cot A$ , using the identity $\csc ^{2}A= 1+\cot ^{2}A$
Answer:
We need to prove -
$\frac{\cos A-\sin A+1}{\cos A+\sin A-1}= cosec A+\cot A$
Dividing the numerator and denominator by $\sin A$ , we get;
$\\=\frac{\cot A-1+\csc A}{\cot A +1-\csc A}\\\\= \frac{(\cot A+\csc A)-(\csc^2 A-\cot^2A)}{\cot A +1-\csc A}\\\\= \frac{(\csc A+\cot A)(1-\csc A+\cot A)}{\cot A +1-\csc A}\\\\= \csc A+\cot A\\\\ =RHS$
Hence Proved.
$(vi)\sqrt{\frac{1+\sin A}{1-\sin A}}= \sec A+\tan A$
Answer:
We need to prove -
$\sqrt{\frac{1+\sin A}{1-\sin A}}= \sec A+\tan A$
Taking LHS;
By rationalising the denominator, we get;
$\\= \sqrt{\frac{1+\sin A}{1-\sin A}\times \frac{1+\sin A}{1+\sin A}}\\\\ = \sqrt{\frac{(1+\sin A)^2}{1-\sin^2A}}\\\\ =\frac{1+\sin A}{\cos A}\\\\ = \sec A + \tan A\\\\ = RHS$
Hence proved.
Q4. Prove the following identities, where the angles involved are acute angles for which the expressions are defined. $(vii)\frac{\sin \theta -2\sin ^{3}\theta }{2\cos ^{3}\theta -\cos \theta }= \tan \theta$
Answer:
We need to prove -
$\frac{\sin \theta -2\sin ^{3}\theta }{2\cos ^{3}\theta -\cos \theta }= \tan \theta$
Taking LHS;
[we know the identity $\cos2\theta = 2\cos^2\theta-1=\cos^2\theta-\sin^2\theta$ ]
$\\\Rightarrow \frac{\sin \theta(1 -2\sin ^{2}\theta) }{\cos\theta(2\cos ^{2}\theta -1) }= \frac{\sin\theta(\sin^2\theta+\cos^2\theta-2\sin^2\theta)}{\cos\theta.\cos2\theta}= \frac{\sin\theta.\cos2\theta}{\cos\theta.\cos2\theta}= \tan\theta =RHS$
Hence proved.
$(viii)(\sin A+\csc A)^{2}+(\cos A+\sec A)^{2}= 7+\tan ^{2}A+\cot ^{2}A$
Answer:
Given the equation,
$(\sin A+\csc A)^{2}+(\cos A+\sec A)^{2}= 7+\tan ^{2}A+\cot ^{2}A$ ..................(i)
Taking LHS;
$(\sin A+\csc A)^{2}+(\cos A+\sec A)^{2}$
$\\\Rightarrow \sin^2 A+\csc^2A +2+\cos^2A+\sec^2A+2= 1+2+2+(1+\cot^2A)+(1+\tan^2A)$
[since $\sin^2\theta +\cos^2\theta = 1, \csc^2\theta-\cot^2\theta =1, \sec^2\theta-\tan^2\theta=1$ ]
$=7+\csc^2A+\tan^2A\\ =RHS$
Hence proved
$(ix)\:(cosec A-\sin A)(\sec A-\cos A)=\frac{1}{\tan A+\cot A}$
[ Hint: Simplify LHS and RHS separately.]
Answer:
We need to prove-
$(coesc A-\sin A)(\sec A-\cos A)=\frac{1}{\tan A+\cot A}$
Taking LHS;
$\\\Rightarrow (cosec A-\frac{1}{\csc A})(\sec A-\frac{1}{\sec A})=\frac{(cosec^2-1)}{cosec A}\times\frac{\sec^2A-1}{\sec A}=\frac{\cot^2A}{cosec A}.\frac{\tan^2A}{\sec A}=\sin A .\cos A$
Taking RHS;
$\\\Rightarrow\frac{1}{\frac{\sin A}{\cos A}+\frac{\cos A}{\sin A}}=\frac{\sin A .\cos A}{\sin^2A+\cos^2A}=\sin A.\cos A$
LHS = RHS
Hence proved.
$(x) (\frac{1+\tan ^{2}A}{1+\cot ^{2}A})= (\frac{1-\tan A}{1-\cot A})^{2}= \tan ^{2}A$
Answer:
We need to prove,
$(\frac{1+\tan ^{2}A}{1+\cot ^{2}A})= (\frac{1-\tan A}{1-\cot A})^{2}= \tan ^{2}A$
Taking LHS;
$\\\Rightarrow \frac{1+\tan ^{2}A}{1+\cot ^{2}A} = \frac{\sec^2A}{\csc^2A}=\tan^2A$
Taking RHS;
$\\=(\frac{1-\tan A}{1-\cot A})^2\\\\= (\frac{1-\frac{\sin A}{\cos A} }{1-\frac{\cos A}{\sin A}})^2\\\\ = \frac{(\cos A -\sin A)^2(\sin^2A)}{(\sin A-\cos A)^2(\cos^2A)}\\\\ =\tan^2A$
LHS = RHS
Hence proved.
Introduction to Trigonometry Class 10 NCERT solutions: Exercise-wise
Exercise-wise NCERT Solutions of Introduction to Trigonometry Class 10 Maths Chapter 8 are provided in the links below.
Class 10 Maths NCERT Chapter 8: Extra Question
Question:
$(\sin \theta+\operatorname{cosec} \theta)^2+(\cos \theta+\sec \theta)^2=$?
Answer:
$(\sin \theta+\operatorname{cosec} \theta)^2+(\cos \theta+\sec \theta)^2$
= $(\sin^2 \theta+\operatorname{cosec}^2 \theta+2\sin \theta\operatorname{cosec} \theta)+(\cos^2 \theta+\sec^2 \theta+2\cos \theta\sec \theta)$
= $\sin^2 \theta+\cos^2 \theta+\operatorname{cosec}^2 \theta+2\sin \theta\operatorname{cosec} \theta+\sec^2 \theta+2\cos \theta\sec \theta$
= $1+1+\cot^2 \theta+2+1+\tan^2 \theta+2$
= $7+\cot^2 \theta+\tan^2 \theta$
Hence, the correct answer is $7+\tan^2 \theta+\cot^2 \theta$.
Introduction to Trigonometry Class 10 Chapter 8: Topics
Students will explore the following topics in NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry:
- 8.1 Introduction
- 8.2 Trigonometric Ratios
- 8.3 Trigonometric Ratios of Some Specific Angles
- 8.4 Trigonometric Identities
Introduction to Trigonometry Class 10 NCERT Solutions - Important Formulae
Arc Length in a Circle:
-
If an arc of length $l$ in a circle with radius $r$ subtends an angle of $\theta$ radians.
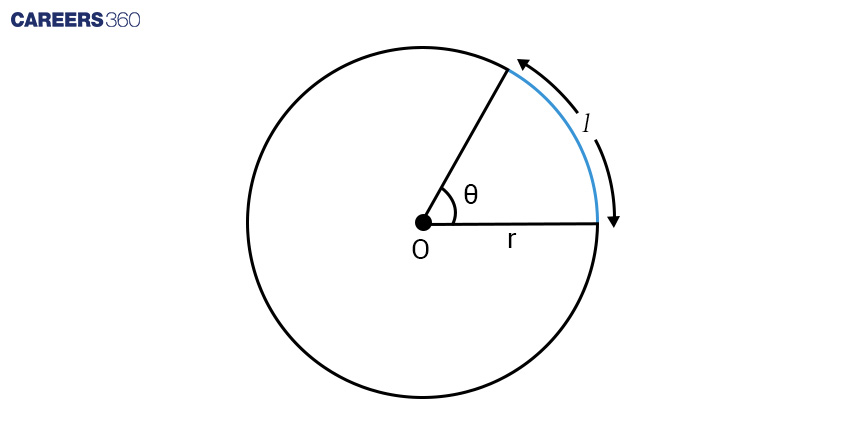
$l = r\theta$ and $θ = \frac{l}{r}$
Conversion Between Radian and Degree Measures:
- Radian Measure = ($\frac{π}{180}$) × Degree Measure
- Degree Measure = ($\frac{180}{π}$) × Radian Measure
Trigonometric Ratios for Right Triangles:
The trigonometric ratios of the angle A in right triangle ABC are defined as follows-
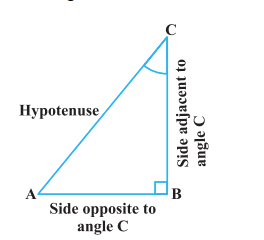
$\begin{aligned} & \text { sine of } \angle A=\frac{\text { side oppositeto angle } A}{\text { hypotenuse }}=\frac{B C}{A C} \\ & \text { cosine of } \angle A=\frac{\text { side adjacent to angle } A}{\text { hypotenuse }}=\frac{A B}{A C} \\ & \text { tangent of } \angle A=\frac{\text { side opposite to angle } A}{\text { side adjacentto angle } A}=\frac{B C}{A B} \\ & \text { cosecant of } \angle A=\frac{\text { hypotenuse }}{\text { side opposite to angle } A}=\frac{A C}{B C} \\ & \text { secant of } \angle A=\frac{\text { hypotenuse }}{\text { side adjacent to angle } A}=\frac{A C}{A B} \\ & \text { cotangent of } \angle A=\frac{\text { side adjacent to angle } A}{\text { side opposite to angle } A}=\frac{A B}{B C}\end{aligned}$
The values of all the trigonometric ratios of 0°, 30°, 45°, 60°, and 90°
| $\angle A$ | 0° | 30° | 45° | 60° | 90° |
|
Sin A |
0 | $\frac{1}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{3}}{2}$ |
1 |
|
Cos A |
1 | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{2}$ |
0 |
|
Tan A |
0 | $\frac{1}{\sqrt{3}}$ |
1 | $\sqrt{3}$ |
Not Defined |
|
Cosec A |
Not Defined |
2 | $\sqrt{2}$ | $\frac{2}{\sqrt{3}}$ |
1 |
|
Sec A |
1 | $\frac{2}{\sqrt{3}}$ | $\sqrt{2}$ |
2 |
Not Defined |
|
Cot A |
Not Defined | $\sqrt{3}$ |
1 | $\frac{1}{\sqrt{3}}$ |
0 |
Also, in a right triangle with an angle $\theta$
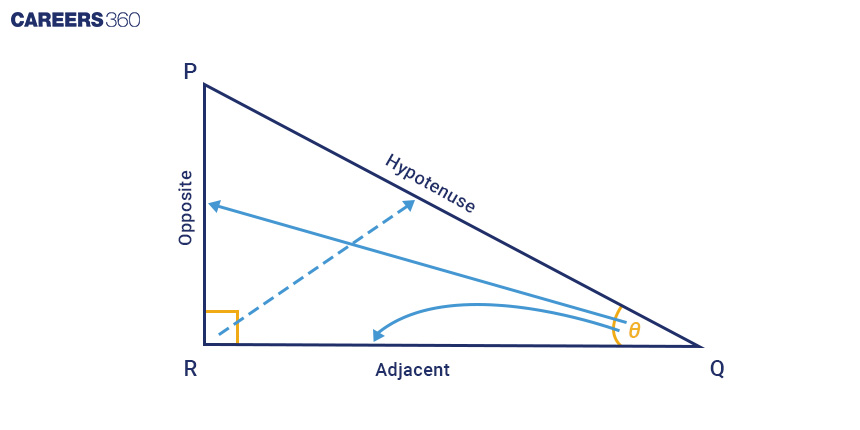
-
sin θ = Opposite/Hypotenuse
-
cos θ = Adjacent/Hypotenuse
-
tan θ = Opposite/Adjacent
-
cosec θ = Hypotenuse/Opposite
-
sec θ = Hypotenuse/Adjacent
-
cot θ = Adjacent/Opposite
Reciprocal Trigonometric Ratios:
-
sin θ = 1/(cosec θ)
-
cosec θ = 1/(sin θ)
-
cos θ = 1/(sec θ)
-
sec θ = 1/(cos θ)
-
tan θ = 1/(cot θ)
-
cot θ = 1/(tan θ)
Trigonometric Ratios of Complementary Angles:
For an angle 'θ', the trigonometric ratios of its complementary angle (90° – θ) are:
-
sin (90° – θ) = cos θ
-
cos (90° – θ) = sin θ
-
tan (90° – θ) = cot θ
-
cot (90° – θ) = tan θ
-
sec (90° – θ) = cosec θ
-
cosec (90° – θ) = sec θ
Trigonometric Identities:
-
sin2 θ + cos2 θ = 1
-
sin2 θ = 1 – cos2 θ
-
cos2 θ = 1 – sin2 θ
-
cosec2 θ – cot2 θ = 1
-
cot2 θ = cosec2 θ – 1
-
sec2 θ – tan2 θ = 1
-
tan2 θ = sec2 θ – 1
Here are some more trigonometric identities that will help students in higher classes.

Why are Class 10 Maths Chapter 8 Introduction to Trigonometry question answers important?
Trigonometry helps us understand the relationship between angles and sides in a right-angled triangle. This chapter introduces the basic trigonometric ratios and their uses in solving problems. These Class 10 Maths Chapter 8 Introduction to Trigonometry question answers help students understand these ideas step by step. Here are some more points on why these question answers are important:
- These solutions help you learn how to find unknown sides and angles using trigonometric ratios.
- These question answers make it easier to remember and apply trigonometric identities in problems.
- These Class 10 Maths Chapter 8 Introduction to Trigonometry question answers prepare you for higher classes where trigonometry is used in calculus, geometry, and physics.
NCERT Solutions for Class 10 Maths: Chapter Wise
We at Careers360 compiled all the NCERT class 10 Maths solutions in one place for easy student reference. The following links will allow you to access them.
Also read,
-
NCERT Notes Class 10 Maths Chapter 8 Introduction to Trigonometry
-
NCERT Exemplar Class 10 Maths Solutions Chapter 8 Introduction To Trigonometry And Its Equations
NCERT Exemplar Solutions - Subject Wise
Given below are the subject-wise exemplar solutions of class 10 NCERT:
NCERT Books and NCERT Syllabus
Here are some useful links for NCERT books and the NCERT syllabus for class 10:
Frequently Asked Questions (FAQs)
An equation involving trigonometric ratios that is true for all values of θ (where the ratios are defined) is called a trigonometric identity.
Trigonometric ratios are the ratios of sides in a right-angled triangle with respect to an acute angle.
They are: sin, cos, tan, cosec, sec, and cot.
The term comes from the Greek words ‘trigonon’ (triangle) and ‘metron’ (measure), meaning measurement of triangles.
These NCERT Solutions for Class 10 Maths Chapter 8 contain the basic concepts of trigonometry, like trigonometric ratios, trigonometric identities, and their applications in the real world.
The easiest way to understand trigonometric ratios is by taking a right-angle triangle, where sine, cosine, and tangent represent ratios of different sides as
sin θ = Opposite / Hypotenuse
cos θ = Adjacent / Hypotenuse
tan θ = Opposite / Adjacent
To solve trigonometric identities in Class 10 Maths Chapter 8, use the basic trigonometric identities as sin2 θ + cos2 θ = 1 and try to express terms in sine and cosine. Also, use simplification and factorisation to solve these types of problems.
To score full marks in Class 10 Trigonometry, memorise all the important trigonometric ratios, identities, and formulas. Practice NCERT examples, exercises, and questions from the previous years. Also, regularly revise and give mock tests to improve scores.
Trigonometry is used in various fields of real life. It is mainly used for calculating the height and distance of real-life objects, and for building bridges and roads. Also, it is used in navigation systems like GPS.
Questions related to CBSE Class 10th
On Question asked by student community
Hello,
The link to the question paper is attached here. You can also find the answer key on the website of Careers360. Careers360 also provide student with preparation tips that will help them utilise their time in preparation.
https://school.careers360.com/articles/cbse-sahodaya-class-10-pre-board-question-paper-2025-26
Thank you.
Hello,
The link to the question paper is attached here. You can also find the answer key for the subjects on the careers360 website that will help you analyse in-depth performance.
https://school.careers360.com/articles/chennai-sahodaya-question-paper-2025-26
Thank you
Hello
You will be able to download the CBSE Class 10th Sample Paper 2025-26 from our official website, careers360, by using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-10th-maths-sample-papers-2025-26
Thank you.
Hello,
The link to the question paper is attached here. You can also find the answer key that will help you analyse your in-depth performance. Careers360 provides students with preparation tips that will help them utilise their time correctly in preparation
https://school.careers360.com/boards/cbse/cbse-pre-board-sample-paper-2025-26
Thank you
Hello,
The CBSE board under Sahodaya School Complexes conducts the Sahodaya School Complex Examination. This examination is based on the latest CBSE syllabus and guidelines.
Practicing with the Sahodaya question papers will give one an overview of the entire examination pattern of the finals, it's marking scheme and types of
Popular CBSE Class 10th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
