NCERT solutions for class 10 maths Chapter 13 Statistics
Hey!! Are you still wondering about reading this article and looking at the solutions or not? Then let me tell you, do not think twice and start reading without confusion, as these solutions are prepared specifically for every type of student in a friendly manner, with brief introductions to important concepts. Let me explain to you what the NCERT Class 10 chapter 13 Statistics is about. Statistics is the art of turning numbers into stories. It teaches us that every number has a voice and every graph can show us a story. This chapter will focus on the measurement of central tendencies like median, mode, and mean to analyse the grouped and ungrouped data. These NCERT solutions for Class 10 Maths will clear all your doubts about the exercise of this chapter and teach you several new problem-solving methods.
This Story also Contains
- NCERT Solutions for Class 10 Maths Chapter 13 Statistics: Download Free PDF
- NCERT Solutions for Class 10 Maths Chapter 13 Statistics (Exercises)
- Statistics Class 10 NCERT Solutions: Exercise-wise
- Class 10 Maths NCERT Chapter 13: Extra Question
- Statistics Class 10 Chapter 13: Topics
- NCERT Solutions For Statistics Class 10 Chapter 13: Important Formulae
- Why are Class 10 Maths Chapter 13 Statistics question answers important?
- NCERT Solutions for Class 10 Maths: Chapter Wise
Statistics is like detective work with numbers: we collect clues (data), sort them, and find out what story they tell! Our academic team here at Careers360 comprises experienced experts with years of teaching experience who have developed these NCERT Solutions for Class 10 content based on the latest NCERT Syllabus. Students preparing for the Class 10 board exams must go through these solutions to strengthen basic concepts, along with learning how to solve these questions, so that they can solve similar questions on their own. Many teachers recommend NCERT Solutions because they closely match the exam pattern. Check this NCERT article for complete syllabus coverage along with NCERT Books, Solutions, Syllabus, and Exemplar Problems with Solutions.
NCERT Solutions for Class 10 Maths Chapter 13 Statistics: Download Free PDF
These NCERT Solutions for Class 10 Maths Chapter 13 Statistics have been prepared by Careers360 experts to make learning simpler and to help you score better in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 10 Maths Chapter 13 Statistics (Exercises)
Below, you will find the NCERT Class 10 Maths Chapter 13 Statistics question answers explained step by step.
|
Statistics Class 10 Question Answers |

Which method did you use to find the mean, and why?
Answer:
|
Number of plants
|
Number of houses $f_i$ |
Classmark $x_i$ |
$f_ix_i$ |
|
0-2 |
1 |
1 |
1 |
|
2-4 |
2 |
3 |
6 |
|
4-6 |
1 |
5 |
5 |
|
6-8 |
5 |
7 |
35 |
|
8-10 |
6 |
9 |
54 |
|
10-12 |
2 |
11 |
22 |
|
12-14 |
3 |
13 |
39 |
|
|
$\sum f_i$ =20 |
|
$\sum f_ix_i$ =162 |
Mean,
$\overline x = \frac{\sum f_ix_i}{\sum f_i}$
$= \frac{162}{20} = 8.1$
We used the direct method in this as the values of $x_i$ and $f_i$ are small.
Q2: Consider the following distribution of daily wages of 50 workers of a factory. Find the mean daily wages of the workers of the factory by using an appropriate method.

Answer:
Let the assumed mean be a = 550
|
Daily Wages |
Number of workers $f_i$ |
Classmark $x_i$ |
$d_i = x_i -a$ |
$f_id_i$ |
|
500-520 |
12 |
510 |
-40 |
-480 |
|
520-540 |
14 |
530 |
-20 |
-280 |
|
540-560 |
8 |
550 |
0 |
0 |
|
560-580 |
6 |
570 |
20 |
120 |
|
580-600 |
10 |
590 |
40 |
400 |
|
|
$\sum f_i$ = 50 |
|
|
$\sum f_i d_i$ = -240
|
Mean,
$\overline x =a + \frac{\sum f_id_i}{\sum f_i}$
$= 550 + \frac{-240}{50} = 550-4.8 = 545.20$
Therefore, the mean daily wages of the workers of the factory is Rs. 545.20.

Answer:
|
Daily pocket allowance |
Number of children $f_i$ |
Classmark $x_i$ |
$f_ix_i$ |
|
11-13 |
7 |
12 |
84 |
|
13-15 |
6 |
14 |
84 |
|
15-17 |
9 |
16 |
144 |
|
17-19 |
13 |
18 |
234 |
|
19-21 |
f |
20 |
20f |
|
21-23 |
5 |
22 |
110 |
|
23-25 |
4 |
24 |
96 |
|
|
$\sum f_i$ = 44 + f |
|
$\sum f_ix_i$ = 752 + 20f |
Mean,
$\overline x = \frac{\sum f_ix_i}{\sum f_i}$
$⇒18 = \frac{752+20f}{44+f}$
$⇒18(44+f) =( 752+20f)$
$⇒ 2f = 40 $
$⇒ f = 20$
Therefore, the missing f = 20.

Answer:
Let the assumed mean be a = 75.5
|
No. of heartbeats per minute |
Number of women $f_i$ |
Classmark $x_i$ |
$d_i = x_i -a$ |
$f_id_i$ |
|
65-68 |
2 |
66.5 |
-9 |
-18 |
|
68-71 |
4 |
69.5 |
-6 |
-24 |
|
71-74 |
3 |
72.5 |
-3 |
-9 |
|
74-77 |
8 |
75.5 |
0 |
0 |
|
77-80 |
7 |
78.5 |
3 |
21 |
|
80-83 |
4 |
81.5 |
6 |
24 |
|
83-86 |
2 |
84.5 |
9 |
18 |
|
|
$\sum f_i$ = 30 |
|
|
$\sum f_id_i$ = 12 |
Mean,
$\overline x =a + \frac{\sum f_id_i}{\sum f_i}$
$= 75.5 + \frac{12}{30} = 75.5 + 0.4 = 75.9$
Therefore, the mean heartbeats per minute of these women are 75.9.

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Answer:
Let the assumed mean be a = 57
|
Number of mangoes |
Number of boxes $f_i$ |
Classmark $x_i$ |
$d_i = x_i -a$ |
$f_id_i$ |
|
50-52 |
15 |
51 |
-6 |
-90 |
|
53-55 |
110 |
54 |
-3 |
-330 |
|
56-58 |
135 |
57 |
0 |
0 |
|
59-61 |
115 |
60 |
3 |
345 |
|
62-64 |
25 |
63 |
6 |
150 |
|
|
$\sum f_i$ = 400 |
|
|
$\sum f_id_i$ = 75 |
Mean,
$\overline x =a + \frac{\sum f_id_i}{\sum f_i}$
$= 57+ \frac{75}{400} = 57+0.1875 = 57.1875 \approx 57.19$
Therefore, the mean number of mangoes kept in a packing box is approximately 57.19.
Q6: The table below shows the daily expenditure on food of 25 households in a locality. Find the mean daily expenditure on food by a suitable method.
|
Daily expenditure in rupees | 100-150 | 150-200 | 200-250 | 250-300 | 300-350 |
| Number of households | 4 | 5 | 12 | 2 | 2 |
Answer:
Let the assumed mean be a = 225 and h = 50
|
Daily Expenditure |
Number of households $f_i$ |
Classmark $x_i$ |
$d_i = x_i -a$ |
$u_i = \frac{d_i}{h}$ |
$f_iu_i$ |
|
100-150 |
4 |
125 |
-100 |
-2 |
-8 |
|
150-200 |
5 |
175 |
-50 |
-1 |
-5 |
|
200-250 |
12 |
225 |
0 |
0 |
0 |
|
250-300 |
2 |
275 |
50 |
1 |
2 |
|
300-350 |
2 |
325 |
100 |
2 |
4 |
|
|
$\sum f_i$ = 25 |
|
|
|
$\sum f_iu_i$ = -7 |
Mean,
$\overline x =a + \frac{\sum f_iu_i}{\sum f_i}\times h$
$= 225 + \frac{-7}{25}\times50 = 225 -14 = 211$
Therefore, the mean daily expenditure on food is Rs. 211.
Find the mean concentration of $SO_2$ in the air.
Answer:
|
Class Interval |
Frequency $f_i$ |
Classmark $x_i$ |
$f_ix_i$ |
|
0.00-0.04 |
4 |
0.02 |
0.08 |
|
0.04-0.08 |
9 |
0.06 |
0.54 |
|
0.08-0.12 |
9 |
0.10 |
0.90 |
|
0.12-0.16 |
2 |
0.14 |
0.28 |
|
0.16-0.20 |
4 |
0.18 |
0.72 |
|
0.20-0.24 |
2 |
0.22 |
0.44 |
|
|
$\sum f_i$ =30 |
|
$\sum f_ix_i$ =2.96 |
Mean,
$\overline x = \frac{\sum f_ix_i}{\sum f_i}$
$= \frac{2.96}{30} = 0.099$
Therefore, the mean concentration of $SO_2$ in the air is 0.099 ppm.
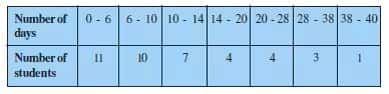
Answer:
|
Number of days |
Number of Students $f_i$ |
Classmark $x_i$ |
$f_ix_i$ |
|
0-6 |
11 |
3 |
33 |
|
6-10 |
10 |
8 |
80 |
|
10-14 |
7 |
12 |
84 |
|
14-20 |
4 |
17 |
68 |
|
20-28 |
4 |
24 |
96 |
|
28-38 |
3 |
33 |
99 |
|
38-40 |
1 |
39 |
39 |
|
|
$\sum f_i$ = 40 |
|
$\sum f_ix_i$ = 499 |
Mean,
$\overline x = \frac{\sum f_ix_i}{\sum f_i}$
$= \frac{499}{40} = 12.475$ $= \frac{499}{40} = 12.475\approx 12.48$
Therefore, the mean number of days a student was absent was 12.48 days.

Answer:
Let the assumed mean be a = 75 and h = 10
|
Literacy rates |
Number of cities $f_i$ |
Classmark $x_i$ |
$d_i = x_i -a$ |
$u_i = \frac{d_i}{h}$ |
$f_iu_i$ |
|
45-55 |
3 |
50 |
-20 |
-2 |
-6 |
|
55-65 |
10 |
60 |
-10 |
-1 |
-10 |
|
65-75 |
11 |
70 |
0 |
0 |
0 |
|
75-85 |
8 |
80 |
10 |
1 |
8 |
|
85-95 |
3 |
90 |
20 |
2 |
6 |
|
|
$\sum f_i$ = 35 |
|
|
|
$\sum f_iu_i$ = -2 |
Mean,
$\overline x =a + \frac{\sum f_iu_i}{\sum f_i}\times h$
$= 70 + \frac{-2}{35}\times10 = 70 -0.57 = 69.43$
Therefore, the mean literacy rate is 69.43%.
|
Statistics Class 10 Question Answers |
Q1: The following table shows the ages of the patients admitted in a hospital during a year:

Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Answer:
The class with the maximum frequency is the modal class.
The maximum frequency is 23, and hence the modal class = 35-45
Lower limit (l) of modal class = 35, class size (h) = 10
Frequency ( $f_1$ ) of the modal class = 23, frequency ( $f_0$ ) of class preceding the modal class = 21, frequency ( $f_2$ ) of class succeeding the modal class = 14.
$Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
$\\ = 35 + \left(\frac{23-21}{2(23)-21-14} \right).10 \\ \\ = 35 + \frac{2}{11}.10$
$= 36.8$
Now,
|
Age
|
Number of patients $f_i$ |
Classmark $x_i$ |
$f_ix_i$ |
|
5-15 |
6 |
10 |
60 |
|
15-25 |
11 |
20 |
220 |
|
25-35 |
21 |
30 |
630 |
|
35-45 |
23 |
40 |
920 |
|
45-55 |
14 |
50 |
700 |
|
55-65 |
5 |
60 |
300 |
|
|
$\sum f_i$ =80 |
|
$\sum f_ix_i$ =2830 |
Mean,
$\overline x = \frac{\sum f_ix_i}{\sum f_i}$
$= \frac{2830}{80} = 35.37$
The maximum number of patients is in the age group of 36.8, whereas the average age of all the patients is 35.37.

Determine the modal lifetimes of the components.
Answer:
The class with the maximum frequency is the modal class.
The maximum frequency is 61, and hence, the modal class = 60-80
Lower limit (l) of modal class = 60, class size (h) = 20
Frequency ( $f_1$ ) of the modal class = 61, frequency ( $f_0$ ) of class preceding the modal class = 52, frequency ( $f_2$ ) of class succeeding the modal class = 38.
$Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
$\\ = 60 + \left(\frac{61-52}{2(61)-52-38} \right)\times20 \\ \\ = 60 + \frac{9}{32}\times20$
$= 65.62$
Thus, the modal lifetime of 225 electrical components is 65.62 hours.
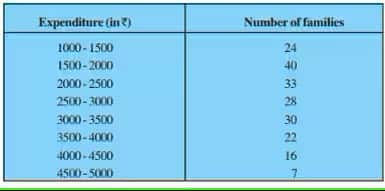
Answer:
The class with the maximum frequency is the modal class.
The maximum frequency is 40, and hence the modal class = 1500-2000
Lower limit (l) of modal class = 1500, class size (h) = 500
Frequency ( $f_1$ ) of the modal class = 40, frequency ( $f_0$ ) of class preceding the modal class = 24, frequency ( $f_2$ ) of class succeeding the modal class = 33.
$Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
$\\ = 1500 + \left(\frac{40-24}{2(40)-24-33} \right).500 \\ \\ = 1500 + \frac{16}{23}.500$
$= 1847.82$
Thus, the Mode of the data is Rs. 1847.82
Now,
Let the assumed mean be a = 2750 and h = 500
|
Expenditure |
Number of families $f_i$ |
Classmark $x_i$ |
$d_i = x_i -a$ |
$u_i = \frac{d_i}{h}$ |
$f_iu_i$ |
|
1000-1500 |
24 |
1250 |
-1500 |
-3 |
-72 |
|
1500-2000 |
40 |
1750 |
-1000 |
-2 |
-80 |
|
2000-2500 |
33 |
2250 |
-500 |
-1 |
-33 |
|
2500-3000 |
28 |
2750 |
0 |
0 |
0 |
|
3000-3500 |
30 |
3250 |
500 |
1 |
30 |
|
3500-4000 |
22 |
3750 |
1000 |
2 |
44 |
|
4000-4500 |
16 |
4250 |
1500 |
3 |
48 |
|
4500-5000 |
7 |
4750 |
2000 |
4 |
28 |
|
|
$\sum f_i$ =200 |
|
|
|
$\sum f_iu_i$ = -35 |
Mean,
$\overline x =a + \frac{\sum f_iu_i}{\sum f_i}\times h$
$= 2750 + \frac{-35}{200}\times500 = 2750 -87.5 = 2662.50$
Thus, the Mean monthly expenditure is Rs. 2662.50.
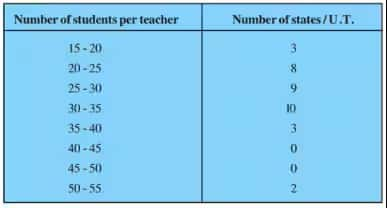
Answer:
The class with the maximum frequency is the modal class.
The maximum frequency is 10, and hence the modal class = 30-35
Lower limit (l) of modal class = 30, class size (h) = 5
Frequency ( $f_1$ ) of the modal class = 10 frequency ( $f_0$ ) of class preceding the modal class = 9, frequency ( $f_2$ ) of class succeeding the modal class = 3
$Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
$\\ = 30 + \left(\frac{10-9}{2(10)-9-3} \right).5 \\ \\ = 30 + \frac{1}{8}.5$
$= 30.625$
Thus, the Mode of the data is 30.625
Now,
Let the assumed mean be a = 32.5 and h = 5
|
Class |
Number of states $f_i$ |
Classmark $x_i$ |
$d_i = x_i -a$ |
$u_i = \frac{d_i}{h}$ |
$f_iu_i$ |
|
15-20 |
3 |
17.5 |
-15 |
-3 |
-9 |
|
20-25 |
8 |
22.5 |
-10 |
-2 |
-16 |
|
25-30 |
9 |
27.5 |
-5 |
-1 |
-9 |
|
30-35 |
10 |
32.5 |
0 |
0 |
0 |
|
35-40 |
3 |
37.5 |
5 |
1 |
3 |
|
40-45 |
0 |
42.5 |
10 |
2 |
0 |
|
45-50 |
0 |
47.5 |
15 |
3 |
0 |
|
50-55 |
2 |
52.5 |
20 |
4 |
8 |
|
|
$\sum f_i$ =35 |
|
|
|
$\sum f_iu_i$ = -23 |
Mean,
$\overline x =a + \frac{\sum f_iu_i}{\sum f_i}\times h$
$= 32.5 + \frac{-23}{35}\times5= 29.22$
Thus, the Mean of the data is 29.22.
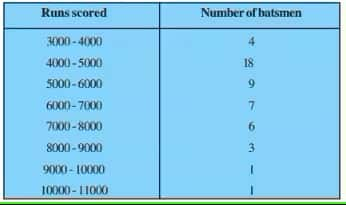
Answer:
The class with the maximum frequency is the modal class.
The maximum frequency is 18, and hence, the modal class = 4000-5000
Lower limit (l) of modal class = 4000, class size (h) = 1000
Frequency ( $f_1$ ) of the modal class = 18 frequency ( $f_0$ ) of class preceding the modal class = 4, frequency ( $f_2$ ) of class succeeding the modal class = 9
$Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
$\\ =4000 + \left(\frac{18-4}{2(18)-4-9} \right).1000 \\ \\ = 4000 + \frac{14}{23}.1000$
$= 4608.70$
Thus, the Mode of the data is 4608.70.

Answer:
The class with the maximum frequency is the modal class.
The maximum frequency is 20, and hence, the modal class = 40-50
Lower limit (l) of modal class = 40, class size (h) = 10
Frequency ( $f_1$ ) of the modal class = 20 frequency ( $f_0$ ) of class preceding the modal class = 12, frequency ( $f_2$ ) of class succeeding the modal class = 11
$Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
$\\ =40+ \left(\frac{20-12}{2(20)-12-11} \right).10 \\ \\ = 40 + \frac{8}{17}.10$
$= 44.70$
Thus, the Mode of the data is 44.70.
|
Statistics Class 10 Question Answers |
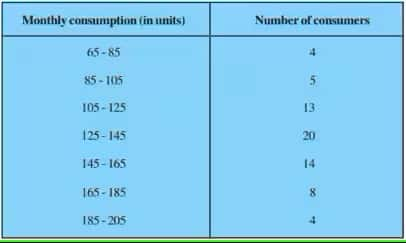
Answer:
Let the assumed mean be a = 130 and h = 20
|
Class |
Number of consumers $f_i$ |
Cumulative Frequency |
Classmark $x_i$ |
$d_i = x_i -a$ |
$u_i = \frac{d_i}{h}$ |
$f_iu_i$ |
|
65-85 |
4 |
4 |
70 |
-60 |
-3 |
-12 |
|
85-105 |
5 |
9 |
90 |
-40 |
-2 |
-10 |
|
105-125 |
13 |
22 |
110 |
-20 |
-1 |
-13 |
|
125-145 |
20 |
42 |
130 |
0 |
0 |
0 |
|
145-165 |
14 |
56 |
150 |
20 |
1 |
14 |
|
165-185 |
8 |
64 |
170 |
40 |
2 |
16 |
|
185-205 |
4 |
68 |
190 |
60 |
3 |
12 |
|
|
|
$\sum f_i = N$ = 68 |
|
|
|
$\sum f_iu_i$ = 7 |
MEDIAN:
$N= 68$
$⇒\frac{N}{2} = 34$
$\therefore$ Median class = 125-145; Cumulative Frequency = 42; Lower limit, l = 125;
c.f. = 22; f = 20; h = 20
$Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W$
$\\ = 125 + \left (\frac{34-22}{20} \right ).20 \\ \\ = 125 + 12$
$= 137$
Thus, the median of the data is 137
MODE:
The class with the maximum frequency is the modal class.
The maximum frequency is 20, and hence the modal class = 125-145
Lower limit (l) of modal class = 125, class size (h) = 20
Frequency ( $f_1$ ) of the modal class = 20; frequency ( $f_0$ ) of class preceding the modal class = 13, frequency ( $f_2$ ) of class succeeding the modal class = 14.
$Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
$\\ = 125 + \left(\frac{20-13}{2(20)-13-14} \right).20 \\ \\ = 125 + \frac{7}{13}.20$
$= 135.76$
Thus, the Mode of the data is 135.76
MEAN:
Mean,
$\overline x =a + \frac{\sum f_iu_i}{\sum f_i}\times h$
$= 130 + \frac{7}{68}\times20 = 137.05$
Thus, the Mean of the data is 137.05.
Q2: If the median of the distribution given below is 28.5, find the values of x and y.
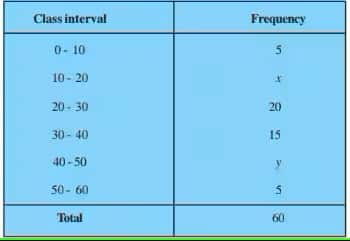
Answer:
|
Class |
Number of consumers $f_i$ |
Cumulative Frequency |
|
0-10 |
5 |
5 |
|
10-20 |
x |
5+x |
|
20-30 |
20 |
25+x |
|
30-40 |
15 |
40+x |
|
40-50 |
y |
40+x+y |
|
50-60 |
5 |
45+x+y |
|
|
$\sum f_i = N$ = 60 |
|
$N= 60$
$⇒\frac{N}{2} = 30$
Now,
Given median = 28.5, which lies in the class 20-30
Therefore, Median class = 20-30
The frequency corresponding to the median class, f = 20
Cumulative frequency of the class preceding the median class, c.f. = 5 + x
Lower limit, l = 20; Class height, h = 10
$Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W$
$\\ \implies28.5= 20 + \left (\frac{30-5-x}{20} \right ).10 \\ \\ \implies8.5=\frac{25-x}{2} \\ \implies 25-x = 8.5(2) \\ \implies x = 25 - 17 = 8$
Also,
$\\ 60 = 45 + x+y \\ \implies x+y = 60-45 = 15 \\ \implies y = 15-x = 15-8 \ \ \ (\because x =8) \\ \implies y = 7$
Therefore, the required values are: x = 8 and y = 7.
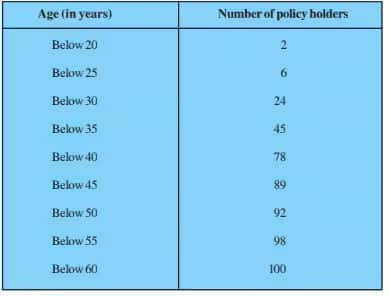
Answer:
|
Class |
Frequency $f_i$ |
Cumulative Frequency |
|
15-20 |
2 |
2 |
|
20-25 |
4 |
6 |
|
25-30 |
18 |
24 |
|
30-35 |
21 |
45 |
|
35-40 |
33 |
78 |
|
40-45 |
11 |
89 |
|
45-50 |
3 |
92 |
|
50-55 |
6 |
98 |
|
55-60 |
2 |
100 |
$N= 100$
$⇒\frac{N}{2} = 50$
Therefore, Median class = 35-45
The frequency corresponding to the median class, f = 21
Cumulative frequency of the class preceding the median class, c.f. = 24
Lower limit, l = 35; Class height, h = 10
$Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W$
$\\ = 35 + \left (\frac{50-45}{33} \right ).5 \\ \\$
$= 35.75$
Thus, the median age is 35.75 years.

Find the median length of the leaves.
(Hint: The data needs to be converted to continuous classes to find the median since the formula assumes continuous classes. The classes then change to
117.5 - 126.5, 126.5 - 135.5, . . ., 171.5 - 180.5.)
Answer:
The data needs to be converted to continuous classes to find the median since the formula assumes continuous classes.
|
Class |
Frequency $f_i$ |
Cumulative Frequency |
|
117.5-126.5 |
3 |
3 |
|
126.5-135.5 |
5 |
8 |
|
135.5-144.5 |
9 |
17 |
|
144.5-153.5 |
12 |
29 |
|
153.5-162.5 |
5 |
34 |
|
162.5-171.5 |
4 |
38 |
|
171.5-180.5 |
2 |
40 |
$ N= 40$
$⇒\frac{N}{2} = 20$
Therefore, Median class = 144.5-153.5
Lower limit, l = 144.5; Class height, h = 9
Frequency corresponding to median class, f = 12
Cumulative frequency of the class preceding the median class, c.f. = 17
$Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W$
$\\ = 144.5 + \left (\frac{20-17}{12} \right ).9 \\ \\$
$= 146.75$
Thus, the median length of the leaves is 146.75 mm.
Q5: The following table gives the distribution of the lifetime of 400 neon lamps :

Find the median lifetime of a lamp.
Answer:
|
Class |
Frequency $f_i$ |
Cumulative Frequency |
|
1500-2000 |
14 |
14 |
|
2000-2500 |
56 |
70 |
|
2500-3000 |
60 |
130 |
|
3000-3500 |
86 |
216 |
|
3500-4000 |
74 |
290 |
|
4000-4500 |
62 |
352 |
|
4500-5000 |
48 |
400 |
$N= 400$
$⇒\frac{N}{2} = 200$
Therefore, Median class = 3000-3500
Lower limit, l = 3000; Class height, h = 500
Frequency corresponding to median class, f = 86
Cumulative frequency of the class preceding the median class, c.f. = 130
$Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W$
$\\ = 3000 + \left (\frac{200-130}{86} \right ).500 \\ \\ = 3000+406.97=3406.97$
Thus, the median lifetime of a lamp is 3406.97 hours.
Answer:
|
Class |
Number of surnames $f_i$ |
Cumulative Frequency |
Classmark $x_i$ |
$f_ix_i$ |
|
1-4 |
6 |
6 |
2.5 |
15 |
|
4-7 |
30 |
36 |
5.5 |
165 |
|
7-10 |
40 |
76 |
8.5 |
340 |
|
10-13 |
16 |
92 |
11.5 |
184 |
|
13-16 |
4 |
96 |
14.5 |
51 |
|
16-19 |
4 |
100 |
17.5 |
70 |
|
|
|
$\sum f_i = N$ = 100 |
|
$\sum f_ix_i$ = 825 |
MEDIAN:
$N= 100 $
$⇒\frac{N}{2} = 50$
$\therefore$ Median class = 7-10; Lower limit, l = 7;
Cumulative frequency of preceding class, c.f. = 36; f = 40; h = 3
$Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W$
$=7+\left(\frac{50-36}{40}\right) \cdot 3$
$= 8.05$
Thus, the median of the data is 8.05
MODE:
The class with the maximum frequency is the modal class.
The maximum frequency is 40, and hence the modal class = 7-10
Lower limit (l) of modal class = 7, class size (h) = 3
Frequency ( $f_1$ ) of the modal class = 40; frequency ( $f_0$ ) of class preceding the modal class = 30, frequency ( $f_2$ ) of class succeeding the modal class = 16
$Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
$\\ = 7 + \left(\frac{40-30}{2(40)-30-16} \right).3 \\ \\ = 125 + \frac{10}{34}.3$
$= 7.88$
Thus, the Mode of the data is 7.88
MEAN:
Mean,
$\overline x =\frac{\sum f_ix_i}{\sum f_i}$
$= \frac{825}{100} = 8.25$
Thus, the Mean of the data is 8.25.

Answer:
|
Class |
Number of students $f_i$ |
Cumulative Frequency |
|
40-45 |
2 |
2 |
|
45-50 |
3 |
5 |
|
50-55 |
8 |
13 |
|
55-60 |
6 |
19 |
|
60-65 |
6 |
25 |
|
65-70 |
3 |
28 |
|
70-75 |
2 |
30 |
MEDIAN:
$N= 30 $
$⇒\frac{N}{2} = 15$
$\therefore$ Median class = 55-60; Lower limit, l = 55;
Cumulative frequency of preceding class, c.f. = 13; f = 6; h = 5
$Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W$
$= 55+ \left (\frac{15-13}{6} \right ).5 $
$ = 55+\frac{2}{6}.5$
$= 56.67$
Thus, the median weight of the students is 56.67 kg.
Statistics Class 10 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Statistics Class 10 Maths Chapter 13 are provided in the links below.
Class 10 Maths NCERT Chapter 13: Extra Question
Question:
Calculate the mean from the following table.
| Scores | Frequencies |
| 0-10 | 2 |
| 10-20 | 4 |
| 20-30 | 12 |
| 30-40 | 21 |
| 40-50 | 6 |
| 50-60 | 3 |
| 60-70 | 2 |
Answer:
The formula for the mean ($X$) using the method of assumed mean is:
$X = A + \frac{\sum fd}{\sum f}$ where $A$ is assumed mean, $f$ is frequency, and $d$ is deviation from mean.
The assumed mean ($A$) is usually taken as the midpoint of the middle class. In this case, it's 35.
The midpoints of the score ranges are 5, 15, 25, 35, 45, 55, and 65.
The frequencies are 2, 4, 12, 21, 6, 3, and 2.
| Midpoint ($x$) | Frequency($f$) | Deviation ($d = x - A$) | $fd$ |
| 5 | 2 | –30 | –60 |
| 15 | 4 | –20 | –80 |
| 25 | 12 | –10 | –120 |
| 35 | 21 | 0 | 0 |
| 45 | 6 | 10 | 60 |
| 55 | 3 | 20 | 60 |
| 65 | 2 | 30 | 60 |
| $\sum f$ = 50 | $\sum fd$ = –80 |
The formula for the mean ($X$) using the method of assumed mean is:
$X = A + \frac{\sum fd}{\sum f}$
⇒ $X = 35 + \frac{-80}{50} = 33.4$
Hence, the correct answer is 33.4.
Statistics Class 10 Chapter 13: Topics
Students will explore the following topics in NCERT Class 10 Maths Chapter 13 Statistics:
- Introduction
- Mean of Grouped Data
- Mode of Grouped Data
- Median of Grouped Data
- Summary
NCERT Solutions For Statistics Class 10 Chapter 13: Important Formulae
Measures of Central Tendency - Mean, Median, and Mode:
Mean:
- Direct Method: The mean, represented as X, can be calculated directly using the formula:
$X = \frac{\sum (f_{i}x_i)}{\sum f_i}$
Where '$f_i$' denotes the frequency of the value '$x_i$'.
-
Assumed Mean Method: Alternatively, the mean can be calculated using the Assumed Mean Method:
$X =a+ \frac{\sum (f_{i}d_i)}{\sum f_i}$
Where '$a$' is an assumed mean and '$d_i$' is the deviation of each value '$x_i$' from the assumed mean.
-
Step Deviation Method: Another approach is the Step Deviation Method:
$X =a+ [\frac{\sum (f_{i}u_i)}{\sum f_i}]\times h$
Where '$u_i$' represents the step deviations and '$h$' is the class interval.
Median:
-
The median is the central value in a set of observations, and its calculation depends on the number of observations.
-
For an odd number of observations,
Median = Value of the $\frac{(n+1)}2$th term in the ordered set
-
In the case of an even number of observations
Median = average of the values of the two middle terms
Median for grouped data
Median $= l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).h$
Where,
$l$ = lower limit of the median class
$c.f $ = Cumulative frequency of preceding class
$f$ = Frequency of median class
$h$ = class interval
Mode:
-
The mode represents the value that appears most frequently in a dataset.
-
The formula to calculate the mode is:
Mode $= l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h$
Where,
$l$ = lower limit of the modal class
$f_1$ = frequency of the modal class
$f_0$ = frequency of the class before the modal class
$f_2$ = frequency of the class after the modal class
$h$ = Class interval
Empirical formula
Mode = 3 Median - 2 Mean
Why are Class 10 Maths Chapter 13 Statistics question answers important?
Understanding statistics helps us make sense of numbers in real life, such as marks, surveys, or averages. It builds our skills to collect, organise, and study data properly. These Class 10 Maths chapter 13 Statistics question answers help us learn these ideas step by step. Here are some more points on why these question answers are important:
- It helps us find the mean, median, and mode easily, which are used to study data in many situations.
- Students get better at solving real-life problems that involve charts, tables, and grouped data.
- It prepares us for higher classes, where we will use statistics in subjects like economics and science.
- Knowing the Class 10 Maths chapter 13 Statistics question answers makes our basics strong for exams and daily data use.
NCERT Solutions for Class 10 Maths: Chapter Wise
We at Careers360 compiled all the NCERT class 10 Maths solutions in one place for easy student reference. The following links will allow you to access them.
Also, read,
NCERT Books and NCERT Syllabus
Here is the latest NCERT syllabus, which is very useful for students before strategising their study plans.
Also, links to some reference books which are important for further studies.
- NCERT Books Class 10 Maths
- NCERT Syllabus Class 10 Maths
- NCERT Books for Class 10 Science
- NCERT Books Class 10
- NCERT Books for Class 10 English
- NCERT Syllabus Class 10
NCERT Exemplar solutions: Subject-wise
You can find NCERT Exemplar Solutions for Maths as well as Science through the given links.
Frequently Asked Questions (FAQs)
There are three methods – the Direct Method, the Assumed Mean Method, and the Step Deviation Method. Each helps calculate the mean, depending on the size and values of the data.
The median helps find the middle value of a data set, useful for calculating average income, age, or marks when the data is unevenly distributed.
They are Mean, Median, and Mode. These help in summarising data through a single representative value.
Yes. Many questions in several state boards, including CBSE Class 10 board exams, come directly or indirectly from NCERT exercises. Practising these solutions ensures better accuracy and speed in exams.
You can easily download free PDFs of NCERT Solutions for Class 10 Maths Statistics from reliable educational websites such as Careers360 for offline study.
In Class 10 Statistics, the mean is the average of all values, the median is the middle value when the data is arranged in order from smallest to largest, and the mode is the value that appears most frequently.
Statistics is widely used in real life to analyse and interpret data. From calculating averages in cricket scores to understanding survey results, this chapter lays a strong foundation for data handling and further studies. Also, NCERT Solutions for Class 10 Maths Chapter 13 Statistics are very important not only for the Class 10 board exam but also for higher classes.
The following topics are covered in NCERT Class 10 Maths Chapter 13:
1. Mean for grouped and ungrouped data.
2. Direct method to find the mean.
3. Method of assumed mean to find the mean.
4. Step deviation method to find the mean.
5. Median for grouped and ungrouped data.
6. Mode for grouped and ungrouped data.
Questions related to CBSE Class 10th
On Question asked by student community
Hello,
The link to the question paper is attached here. You can also find the answer key on the website of Careers360. Careers360 also provide student with preparation tips that will help them utilise their time in preparation.
https://school.careers360.com/articles/cbse-sahodaya-class-10-pre-board-question-paper-2025-26
Thank you.
Hello,
The link to the question paper is attached here. You can also find the answer key for the subjects on the careers360 website that will help you analyse in-depth performance.
https://school.careers360.com/articles/chennai-sahodaya-question-paper-2025-26
Thank you
Hello
You will be able to download the CBSE Class 10th Sample Paper 2025-26 from our official website, careers360, by using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-10th-maths-sample-papers-2025-26
Thank you.
Hello,
The link to the question paper is attached here. You can also find the answer key that will help you analyse your in-depth performance. Careers360 provides students with preparation tips that will help them utilise their time correctly in preparation
https://school.careers360.com/boards/cbse/cbse-pre-board-sample-paper-2025-26
Thank you
Hello,
The CBSE board under Sahodaya School Complexes conducts the Sahodaya School Complex Examination. This examination is based on the latest CBSE syllabus and guidelines.
Practicing with the Sahodaya question papers will give one an overview of the entire examination pattern of the finals, it's marking scheme and types of
Popular CBSE Class 10th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters