Statistics Class 10th Notes - Free NCERT Class 10 Maths Chapter 14 Notes - Download PDF

Statistics is a method of analysing data and converting the row data into a more understandable form. Statistics is used to compute or manipulate numerical data. Generally, statistics is used to compute, manipulate and organise the set of numerical data. If we have large numerical data, then statistics is the best mathematical method to summarize the data in the most representative manner. Statistics is one of the branches of applied mathematics. Statistics is used in many areas, like weather forecasting, where raw numerical data is converted into useful presentable data, and similarly in psychology, geology, sociology, and probability. The real-life application of statistics is in business decision making and sports analytics, where they compare data of different or the same sports persons.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

These notes contain all the topics, subtopics, formulae, and important key points of statistics. These notes cover the basic definition of statistics, what is class interval, frequency, mean, mode and median, types of data and their related subtopics. CBSE Class 10 chapter Statistics also includes the cumulative frequency and formulae. Students must practice all the topics of statistics and their examples from the NCERT Exemplar Solutions for Class 10 Maths Chapter 13 Statistics. Students must practice questions and check their solutions using the NCERT Solutions for Class 10 Maths Chapter 13 Statistics.

NCERT Class 10 Maths Chapter 13 Statistics: Notes

Statistics: Statistics is the branch of applied mathematics that is concerned with analysing, organizing and presenting data more presentable and useful form.

Types of Data

There are two types of data:

1. Ungrouped Data: When data is unorganized or in the form of row data, or an observation is not classified into any group, it is called ungrouped data.

Example: The marks of the students of class 3rd out of 50.
23, 34, 43, 43, 23, 12, 10, 10, 10, 23, 45, 47, 49, 50
This type of ungrouped data is easy to work with, only when the size of the dataset is small.

2. Grouped Data: In grouped data, data are organized organized or in other words, observations are classified.

Example: The ages of different people in a city X are shown in tabulated form.

Here, the number of people in city X is organized in different age intervals. When the large data set is in the grouped form, it is easy to work.

Frequency

The number of times a particular observation appears in the data is known as the frequency.

Class Interval

Data is divided into groups of classes according to the range in a way that all observations belong to that class, and this is called a class interval, and the class width is equal for all datasets.
Class width = Upper class limit - Lower class limit

Mean

Mean is a method of determining the average of a given set of data.

Mean of Grouped Data When Class Interval Not Given:
When grouped data is given but class intervals are not given the the mean will be:

$\bar{x}$ = $\frac{\sum xifi}{\sum fi}$
Where,

$fi$ = Frequency of the ith observation, $xi$.

Example: The ages of the people of country X are given in tabular form. Find the mean age of the people of city X.

In the table, age is called $xi$ and the number of persons is $fi$ and needs to determine the multiplication of $xi$ and $fi$ as shown in the table.

$\bar{x}$ = $\frac{\sum xifi}{\sum fi}$

$\bar{x}$ = $\frac{1645}{41}$

$\bar{x}$ = $40.12$

Methods of Determining the Mean of Group Data:

There are three different methods to determine the mean of group data, and these methods are as follows:

1. Direct Method: In this method, convert the data into class intervals and determine the class width for each class interval and tabulate the multiplication of the class width and intervals and apply the formula of mean.

Example: The ages of the people of country X are given in tabular form. Find the mean age of the people of city X.

Class width = Upper class limit - Lower class limit

$\bar{x}$ = $\frac{\sum xifi}{\sum fi}$

$\bar{x}$ = $\frac{2275}{35}$

$\bar{x}$ = $65$

2. Assumed Mean Method: In this method, convert the data into class intervals and determine the class width for each class interval and determine the deviation and tabulate the multiplication of the class width and deviation and apply the formula of mean.

$Deviation(di)$ = $xi-a$

Where a is the middle term in $xi$.

$\bar{x}$ = $a+$ $\frac{\sum fidi}{\sum fi}$

$\bar{x}$ = $45+$$\frac{700}{35}$

$\bar{x}$ = $65$

3. Step-deviation Method: As in the above example, one more step deviation method has been added in the column to find the mean, and this is as follows,

$ui$ = $\frac{(xi–a)}{h}$
Where,
a = The assumed mean
h = Class size or width

$\bar{x}$ = $a+h$ $\frac{\sum fiui}{\sum fi}$

$\bar{x}$ = $45+10$ $\frac{70}{35}$

$\bar{x}$ = $45+10\times 2$

$\bar{x}$ = $45+20$

$\bar{x}$ = $65$

Relation between the Mean of Step-Deviations (u) and the Mean

$u$i = $\frac{(xi-a)}{h}$

$\bar{u}$ = $\frac{(xi-a)}{h}$

$\bar{u}$ = $\frac{\frac{\sum fi(xi-a)}{h}}{\sum fi}$

$u$i = $\frac{1}{h}\times$ $(\bar{x}-a$

Median

Median is a method of finding the middle value for a given set of numbers. The data must be sorted in any order to determine the median of the provided dataset.

Median of Grouped Data without Class Intervals

There are three steps to determine the medium of the grouped data when no class intervals are given:
1. The first step is to arrange the data in either ascending or descending order.
2. Determine the cumulative frequency.
3. If the number of observations in the given data set is even, then the median can be calculated as,
Median = ${\frac{n}{2}}^{\text{th term}}$ + $(\frac{n}{2}+1{)}^{\text{th term}}$
Where, n = Number of observations

Example: Determine the median for the given data set.
2, 3, 1, 6, 9, 5, 8, 4
After arranging the data in ascending order, we get:
1, 2, 3, 4, 5, 6, 8, 9

Median = $\frac{(\frac{n}{2}{)}^{\text{th term}}+(\frac{n}{2}+1{)}^{\text{th term}}}{2}$
n = 8

Now, putting the values in the formulas,

Median = $\frac{(\frac{8}{2}{)}^{\text{th term}}+(\frac{8}{2}+1{)}^{\text{th term}}}{2}$

Median = $\frac{4^{\text{th term}}+5^{\text{th term}}}{2}$

4^{th term} = 4 and 5^{th term} = 5

Median = $\frac{4+5}{2}$

Median = 4.5

4. If the number of observations in the given dataset is odd, the median can be calculated as,

Median = ($\frac{n+1}{2}{)}^{\text{th term}}$

Where, n = Number of observations

Example: Determine the median for the given data set.
2, 3, 1, 6, 9, 5, 8
After arranging the data in ascending order, we get:
1, 2, 3, 5, 6, 8, 9
Here, n = 7

Median = ($\frac{n+1}{2}{)}^{\text{th term}}$

After putting in the values, we get,

Median = ($\frac{7+1}{2}{)}^{\text{th term}}$

Median = $4^{\text{th term}}$

$4^{\text{th term}}$ = 5

Therefore, median = 5

Cumulative Frequency

The sum of the frequency up to a particular class interval is called the cumulative frequency.

Cumulative Frequency Distribution of Less Than Type

When the number of observations is less than or equal to the particular observation, then it is called the cumulative frequency of the less than type.

Cumulative Frequency Distribution of More than type

When the number of observations is greater than or equal to the particular observation, then it is called the cumulative frequency distribution of the more than type.

Ogive (Cumulative Frequency Graph):

This is the frequency or cumulative distribution graph of a series. It shows data values on the horizontal plane axis, and the percent frequencies on the vertical axis.

Example: In the table weights of 50 boys of class X are given. Find the median weight of the class.

The cumulative frequency is added in the table as shown below:

The Ogive (Cumulative frequency) graph is shown below:

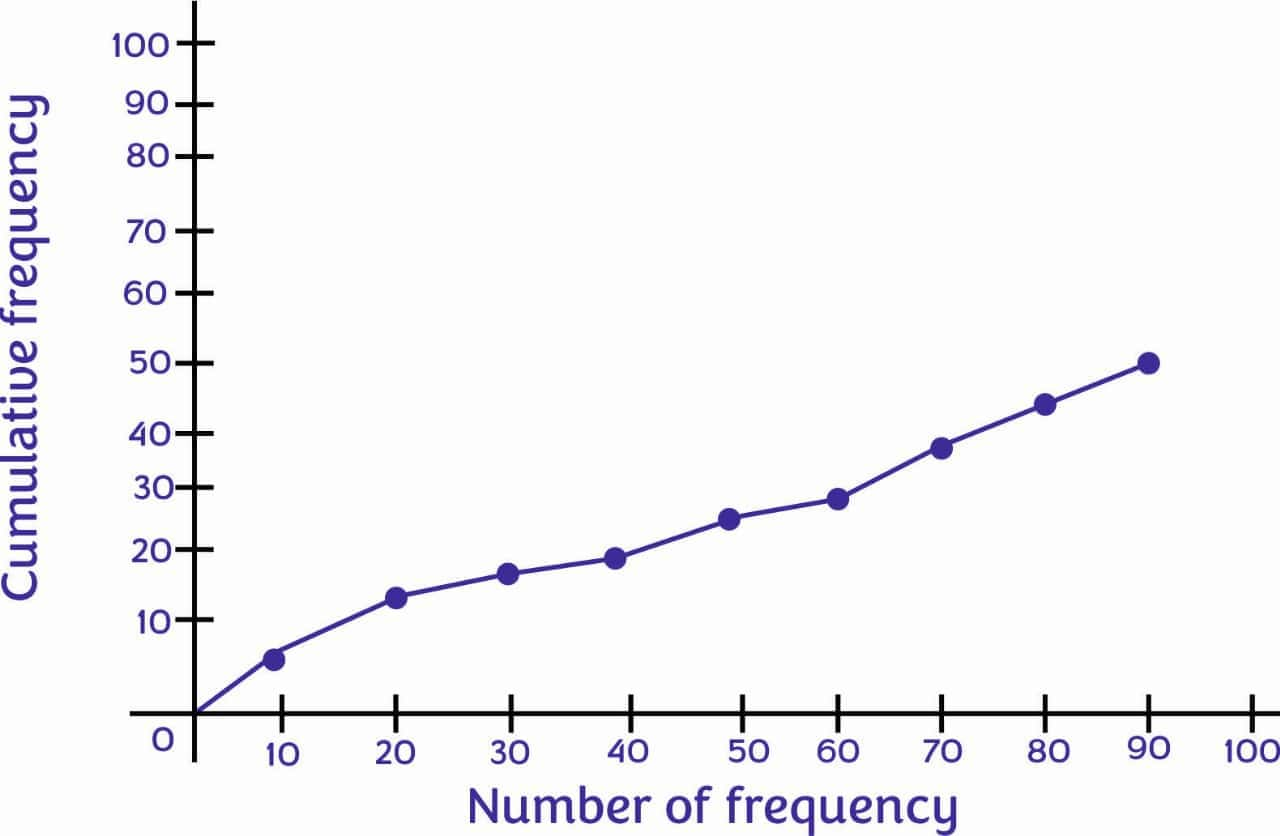
Median of Grouped Data with Class Intervals:

The following steps are used to determine the median of grouped data sets.
1. Determine the cumulative frequency.
2. Apply the formula as:

$Median$ = $l+(\frac{\frac{n}{2}-cf}{f})\times h$

Where,

$l$ = The lower limit of the median class

$n$ = The number of observations

$cf$ = Cummulative frequency

$f$ = Frequency of the class

$h$ = Class size

Example: In the table weights of 50 boys of class X are given. Find the median weight of the class.

The cumulative frequency is added in the table as shown below:

Here, n = 50

And, $\frac{50}{22}$ = 25

Therefore, the observation lies between the class intervals of 50 - 60, and this is called the median class.

Lower class limit (l) = 50

h = 10

Frequency (f) = 3

Cumulative frequency of the class preceding the median class (cf) = 19

$Median$ = $l+(\frac{\frac{n}{2}-cf}{f})\times h$

After putting in the values, we get:

$Median$ = $50+(\frac{\frac{50}{2}-19}{3})\times 10$

$Median$ = $50+(3\times 10)$

$Median$ = $80$

Mode:

The value that has the highest frequency in the given data set is called the mode.

Mode for Grouped Data with Class Intervals

The mode for grouped data with class intervals can be defined as

Mode = $l+(\frac{f1-f0}{2f1-f0-f2})\times h$

Where,
l = Lower limit of the modal class
h = Class size
f₁ = Frequency of the modal class
f₀ = Frequency of the class preceding the modal class
f₂ = Frequency of the class succeeding the modal class

Example: In the table weights of 50 boys of class X are given. Find the mode of the given data.

Mode = $l+(\frac{f1-f0}{2f1-f0-f2})\times h$

In the table, the maximum class frequency is 8, and the class interval is 70 - 80.

Therefore, the model class = 70 - 80
Lower limit of the modal class (l) = 70
Class size (h) = 10
Frequency of the modal class (f1) = 8
Frequency of the class preceding the modal class (f0) = 3
Frequency of the class succeeding the modal class (f2) = 6

After putting in the values, we get:

Mode = $70+(\frac{8-3}{2\times 8-3-6})\times 10$

Mode = $70+(\frac{5}{7})\times 10$

Mode = $70+(\frac{50}{7})$

Mode = $77.14$

Relation Between Mean, Mode and Median:

i) The mean considers all the observations and its value lies between the extreme values. It is used to compare distributions.
ii) In a condition where all the observations are arranged in a particular form or sorted in an order where a particular observation is not important, then in this case median is required. Median does not emphasise only extreme values.
iii) If we require most most frequent values, then the mode is required. The relation between them is as follows,
3 Median = Mode + 2 Mean

Class 10 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics

NCERT Notes For Class 10

The notes are written in a way that they align with the board exam pattern. The class 10 NCERT notes offer point-wise explanations of textbook chapters, highlight important terms and provide a focused preparation for the board exams.

• NCERT Notes for Class 10 Maths

• NCERT Notes for Class 10 Science

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions

• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths

• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10

• NCERT Syllabus for Class 10