NCERT Class 11 Physics Chapter 4 Motion in a Plane Notes - Download PDF
Have you ever seen the way a football flies in the air when it is kicked, or a plane changes its course easily in the air? These are examples of two-dimensional motion where things move in two dimensions as opposed to moving along a straight path.
This Story also Contains
- NCERT Notes for Class 11 Physics Chapter 3: Download PDF
- NCERT Notes for Class 11 Physics Chapter 3
- Class 11 Physics Chapter 3 Motion in a Plane: Previous Year Question and Answer
- How to Master Class 11 Physics Chapter 3 Motion in a Plane?
- Importance of Class 11 Physics Chapter 3 Motion in a Plane
- How to Use NCERT Class 11 Physics Chapter 3 Notes Effectively?
- NCERT Class 12 Notes Chapter-Wise
- NCERT Books and Syllabus
The NCERT Notes for Class 11 Physics Chapter 3 Motion in a Plane, give a proper and clear explanation of such motion in terms of vectors, their components and math tools. In contrast to linear motion that has been studied in the previous chapter, most real-world motions are at angles, and that is why vectors are necessary to represent such physical quantities as displacement, velocity and force. These Class 11 Physics NCERT notes are written according to the current CBSE syllabus with brief theory, solved examples, and key formulae to make learning easier. These NCERT Notes for Class 11 Physics Chapter 3 Motion in a Plane are not only beneficial in preparation for Board examinations but also in the development of a competitive examination, such as in JEE and NEET. Through the revision of these notes, NCERT questions, and attention to major problem-solving strategies, students will be able to reinforce their concepts and increase their exam results.
Also Read
NCERT Notes for Class 11 Physics Chapter 3: Download PDF
Class 11 Physics Chapter 3 Motion in a Plane Notes PDF provides a structured explanation of vector concepts, projectile motion, and uniform circular motion with solved examples and key formulas. These downloadable Motion in a Plane Class 11 Physics notes are designed to make revision easier and are highly useful for CBSE exams as well as competitive exams like JEE and NEET.
NCERT Notes for Class 11 Physics Chapter 3
Class 11 Physics Chapter 3 Motion in a Plane Notes offer students simplified concepts of the two-dimensional motion with the help of vectors, formulas and solved examples. These Motion in a Plane Class 11 Physics Chapter 3 CBSE notes are written according to the latest CBSE syllabus in order to assist in efficient revision. They simplify the preparation of exams, both board and competitive, such as JEE and NEET, with brief points, illustrations and main concepts.
Scalars And Vectors
Scalar
-
A scalar has only magnitude (size).
-
You get it by multiplying the number by the unit of the quantity.
-
Examples: Mass, Speed, Distance
-
You can add, subtract, and multiply scalars using simple math.
Vector
-
A vector has both magnitude and direction.
-
They follow the rules of vector addition like:
- Examples: Displacement, Velocity, Acceleration, Force
- The magnitude of a vector is represented by $|\vec{A}|$ or $A$. Vectors are shown with an arrow.
Representation of a vector
- A vector looks like a line with an arrow.
- The length of the arrow shows the magnitude.
- The direction of the arrow shows the direction of the vector.
A vector can be represented geometrically as a directed line segment with an arrowhead. The arrow's length represents the magnitude of the vector, and it points in the same direction as the vector itself. Tail $\xrightarrow[\text { (magnitude) }]{\text { Length }}$ Head
Types of Vector
- Equal vectors: If the magnitudes and directions of vectors A and B are the same, they are equal.
- Parallel vectors are A and B when: 1. They both point in the same direction. 2. Two vectors can be expressed as scalar (positive) non-zero multiples of each other.
- Antiparallel vectors: A and B are anti-parallel if their directions are opposite.
One vector is a negative multiple of the other that is not zero.
A vector with 0 magnitude and an arbitrary (unknown) direction is called a zero vector. -
Unit vector: A unit vector is a vector with a fixed magnitude that points in a specific direction. A vector $(\vec{A})$ can be expressed as the product of a unit vector (Â) in its direction and magnitude.
- A unit vector has no dimensions or units. Unit vectors along the positive x, y, and z axes of a rectangular coordinate system are denoted by î, $\hat{j}$, and k̂, respectively. such that
Position and Displacement Vectors
A position vector is a vector that represents the location of a point or a particle in space with respect to a fixed origin. It is usually denoted by $\vec{r}$ and is drawn from the origin to the location of the object.
If a particle is located at point
A displacement vector represents the change in position of a particle. It is defined as the vector that points from the initial position to the final position of the object.
If the position vector of the initial point is $\vec{\eta}_1$ and the final point is $\vec{r}_2$, then the displacement is given by:
$
\overrightarrow{\Delta r}=\vec{r}_2-\vec{r}_1
$
Displacement is a vector quantity, having both magnitude and direction, and is independent of the actual path taken.
Equality of Vectors
Two vectors are said to be equal if they have the same magnitude and the same direction, regardless of their initial points.
That is, if $\vec{A}$ and $\vec{B}$ satisfy:
$
|\vec{A}|=|\vec{B}| \text { and Direction of } \vec{A}=\text { Direction of } \ \vec{B}
$
then $\vec{A}=\vec{B}$.
This means that vectors can be moved parallel to themselves in space without changing their properties, as long as magnitude and direction are preserved.
Multiplication of Vectors by Real Numbers
If $\vec{A}$ is a vector and $\lambda$ is a real number (scalar), then the product $\lambda \vec{A}$ is also a vector
- The magnitude of $\lambda \vec{A}$ is $|\lambda||\vec{A}|$.
- The direction of $\lambda \vec{A}$ is the same as $\vec{A}$ if $\lambda>0$, and opposite to $\vec{A}$ if $\lambda<0$.
Addition and Subtraction of Vectors — Graphical Method
Either the triangle law or the parallelogram law can be used to add vectors:
(A) Parallelogram law of addition of vectors: The diagonal drawn through the intersection of two vectors, A and B, represents the resultant vector if they are represented by two adjacent sides of a parallelogram, both pointing outward from a common point (with their tails coinciding).
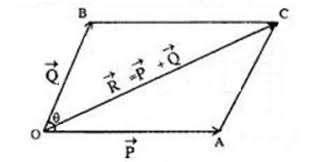
$R=\sqrt{P^2+Q^2+2 P Q \cos \theta}$
(B) The Triangle Law of Vector Addition states that if two vectors are represented by two triangle sides, then the third side of the triangle represents their total or resultant vector, but in the opposite direction.
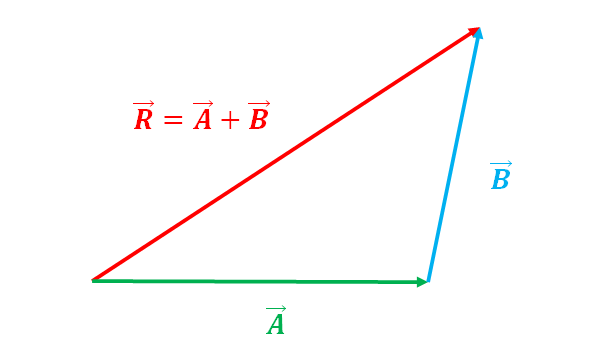
Subtraction of Vectors
To subtract vector $\vec{B}$ from $\vec{A}$, we add $\vec{A}$ and the negative of vector $\vec{B}$.
$
\vec{A}-\vec{B}=\vec{A}+(-\vec{B})
$
- Reverse the direction of $\vec{B}$ to get $-\vec{B}$.
- Then use either the triangle law or parallelogram law to add $\vec{A}$ and $-\vec{B}$.
Multiplication of Vectors $\vec{a} \cdot \vec{b}=a_x b_x+a_y b_y+a_z b_z=a b \cos \theta$
Vector Product (Cross Product): The vector product or cross product of two vectors $\vec{a}$ and $\vec{b}$, denoted as $\vec{a} \times \vec{b}$, is a vector quantity defined as follows:
$
\begin{gathered}
\vec{a} \times \vec{b}=\left(a_y b_z-a_z b_y\right) \hat{\imath}+\left(a_z b_x-a_x b_z\right) \hat{\jmath}+\left(a_x b_y-a_y b_x\right) \hat{k} \\
|\vec{a} \times \vec{b}|=a b \sin \theta
\end{gathered}
$
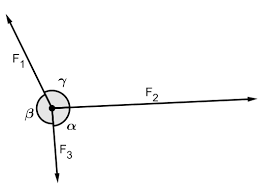
Lami’s Theorem:
- Lami's Theorem states that each force is proportional to the sine of the angle generated by the other two forces if three forces operating at the same spot are in equilibrium.
Resolution of Vectors
Resolution of a vector is the process of expressing a single vector as the sum of two or more vectors (called components), usually along mutually perpendicular directions (like the
If a vector $\vec{A}$ makes an angle $\theta$ with the x -axis, then:
$
\begin{array}{ll}
\vec{A}_x=A \cos \theta & \text { (component alongx-axis) } \\
\vec{A}_y=A \sin \theta & \text { (component alongy-axis) }
\end{array}
$
Thus, the vector $\vec{A}$ can be written as:
$
\vec{A}=\vec{A}_x \hat{i}+\vec{A}_y \hat{j}=A \cos \theta \hat{i}+A \sin \theta \hat{j}
$
Vector Addition – Analytical Method
Let two vectors $\vec{A}$ and $\vec{B}$ be added. Suppose:
$\vec{A}$ has components $A_x$ and $A_y$, and
$\vec{B}$ has components $B_x$ and $B_y$
Then the resultant vector $\vec{R}=\vec{A}+\vec{B}$ has components:
$
\begin{aligned}
& R_x=A_x+B_x \\
& R_y=A_y+B_y
\end{aligned}
$
Now, the magnitude of the resultant vector is:
$
|\vec{R}|=\sqrt{R_x^2+R_y^2}=\sqrt{\left(A_x+B_x\right)^2+\left(A_y+B_y\right)^2}
$
And the direction (angle $\theta$ with the $x$-axis) is given by:
$
\tan \theta=\frac{R_y}{R_x}=\frac{A_y+B_y}{A_x+B_x}
$
Motion in a Plane
In motion in a plane, the position, velocity, and acceleration of an object are all described using vectors.
The motion can be analysed by breaking it into two perpendicular directions, usually the
The position vector of an object at any instant is given by:
$
\vec{r}=x(t) \hat{i}+y(t) \hat{j}
$
The velocity vector is the time derivative of the position vector:
$
\vec{v}=\frac{d \vec{r}}{d t}=v_x \hat{i}+v_y \hat{j}
$
The acceleration vector is the derivative of velocity:
$
\vec{a}=\frac{d \vec{v}}{d t}=a_x \hat{i}+a_y \hat{j}
$
Projectile Motion
A body that is propelled with some initial velocity—not including vertical upward or downward motion—is called a projectile. Once in motion, the projectile moves only due to gravity; it is not further propelled by an engine, fuel, or other external source. A projectile's trajectory is the course it takes while in motion.
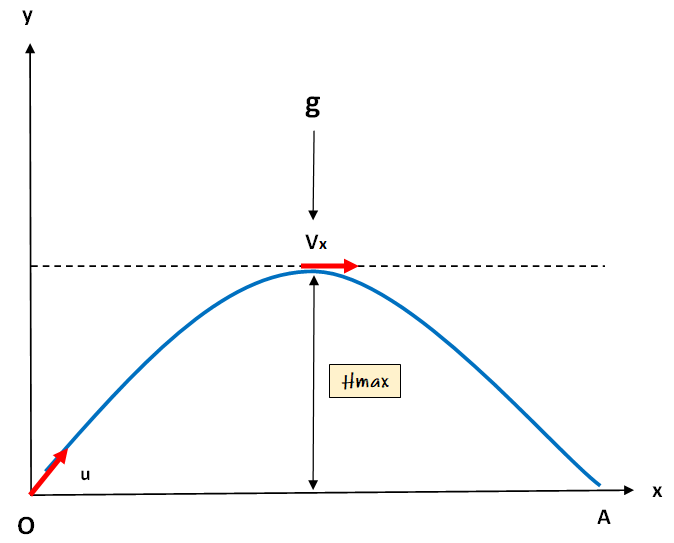
- For motion along the X-axis,
$
v_x=u_x+a_x \operatorname{tand} x=x_0+u_x t+\frac{1}{2} a_x t^2
$
- For motion along the Y-axis,
$
v_y=u_y+a_y \operatorname{tand} y=y_0+u_y t+\frac{1}{2} a_y t^2
$
- Angular projection of the projectile :
1. Time of flight ( T ):
$
\mathrm{T}=\frac{2 u \sin \theta}{g}
$
2. Maximum height(h):
$
h=\frac{u^2 \sin ^2 \theta}{2 g}
$
3. Horizontal range $(\mathrm{R})$ :
$
\mathrm{R}=\frac{u^2 \sin 2 \theta}{g}
$
4. Maximum horizontal range( $\mathrm{R}_{\max }$ ):
$
R_{\max }=\frac{u^2}{g} \text { for } \theta=45^{\circ}
$
Note: For maximum range, $\theta$ should be 45 degrees.
Equation of trajectory
A trajectory is the term used to describe the body's journey. We must determine the link between y and x and eliminate time in order to build the trajectory.
|
Horizontal Motion |
Vertical Motion |
| $\begin{gathered}u_x=u \cos \theta \\ a_x=0 \\ s_x=u \cos \theta t=x\end{gathered}$ |
|
Uniform Circular Motion
When an object moves in a circular path with constant speed, the motion is called Uniform Circular Motion (UCM). Although the speed remains constant, the direction of velocity changes continuously, making it an accelerated motion.
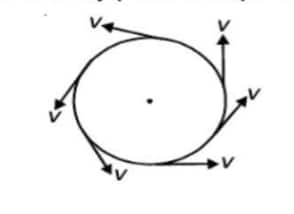
- Speed is constant, but velocity changes due to a change in direction.
- The object experiences a centripetal acceleration directed towards the centre of the circular path.
- A centripetal force is required to keep the object moving in a circle, also directed towards the centre.
- Angular Velocity: $\omega=\frac{2 \pi}{T}$ (radians per second)
- Relation between $v$ and $\omega$ :
$
v=r \omega
$
- Centripetal Acceleration:
$
a_c=\frac{v^2}{r}=r \omega^2
$
- Centripetal Force: $F_c=m a_c=\frac{m v^2}{r}$
Class 11 Physics Chapter 3 Motion in a Plane: Previous Year Question and Answer
Chapter 3, Motion in a Plane, introduces motion in two dimensions using vectors, projectile motion, and uniform circular motion. To understand these concepts deeply, solving previous year questions is extremely helpful as they highlight important patterns and commonly tested concepts. These questions strengthen numerical problem-solving and conceptual clarity, helping students perform well in school exams and competitive exams.
Q1:
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
(a) The magnitude of particle velocity (speed) remains constant.
(b) Particle velocity remains directed perpendicular to the radius vector.
(c) The direction of acceleration keeps changing as the particle moves.
(d) Angular momentum is constant in magnitude, but direction keeps changing.
Answer:
The correct answers are:
a: Speed is constant at all times in the case of uniform circular motion
b: In the case of velocity, in a circular motion, it is measured tangentially to the direction of motion of the particle, which is, in turn, perpendicular to the radius.
c: The direction of the acceleration is always in the direction of the force. This can concur with Newton’s second law of motion. So as the particle moves in a circular motion, the direction of force keeps on changing, and hence that of acceleration also changes.
Q2:
The horizontal range of a projectile fired at an angle of $15^{\circ}$ is 50 m. If it is fired with the same speed at an angle of $45^{\circ}$, its range will be:
(a) 60m
(b) 71m
(c) 100m
(d) 171m
Answer:
According to the formula:
$
R=\frac{u^2 \sin 2 \theta}{g}
$
Given in the question:
$
\theta=15, R=50 \mathrm{~m}
$
Putting in the formula, we get:
$
u^2=100 \mathrm{~g}
$
For $\theta=45$,
The value of the range is:
$
R=\frac{100 \mathrm{~g} \times \sin 90}{g}=100 \mathrm{~m}
$
Hence, the correct answer is option (c).
Q3:
Following are four different relations about displacement, velocity, and acceleration for the motion of a particle in general. Choose the incorrect one(s) :
(a) $v_{a v}=\frac{1}{2}\left[v\left(t_1\right)+v\left(t_2\right)\right]$
(b) $v_{a v}=\frac{r\left(t_2\right)-r\left(t_1\right)}{t_2-t_1}$
(c) $r=\frac{1}{2}\left(v\left(t_2\right)-v\left(t_1\right)\right)\left(t_2-t_1\right)$
(d) $a_{a v}=\frac{v\left(t_2\right)-v\left(t_1\right)}{t_2-t_1}$
Answer:
The given relation is correct when the acceleration is uniform
$
\vec{r}=\frac{1}{2}\left(\vec{v}\left(t_2\right)-\vec{v}\left(t_1\right)\right)\left(t_2-t_1\right)
$
This is the relationship given in the question, but it is not possible as the LHS and RHS dimensions $\left[M^0 L^1 T^0\right]$ do not match, and hence the relationship cannot be considered valid $
Hence, the answer is option (a).
How to Master Class 11 Physics Chapter 3 Motion in a Plane?
Chapter 3, Motion in a Plane, of Class 11 Physics describes the vectors used to explain object motion in two dimensions. The chapter presents the operations of vectors, projectile motion, the relative velocity and circular motion- the important topics to develop powerful problem-solving skills. In order to achieve mastery of this chapter, the students need to learn by visualising the concepts and then using them to solve numerical problems.
- Start by having a clear idea of vectors, their components and how vectors add or subtract, since the whole chapter is based on vector mathematics.
- Practice solving vectors in horizontal and vertical components in order to make the calculation and understanding of 2D motion easier.
- Study thoroughly the concepts of projectile motion, and pay attention to the fact that horizontal and vertical motions are independent of each other.
- Draw neat diagrams for displacement, velocity, and projectile paths to visualise problems better.
- Study the principle of relative velocity, particularly of river-boat and rain-wind problems, which are so frequently asked in the exam.
- Study uniform circular motion by understanding centripetal acceleration and how velocity continuously changes direction.
- Create precision and speed by solving a broad range of numerical questions from NCERT textbook, NCERT Exemplar and sample papers.
- Look through significant graphs such as displacement-time and velocity-time in two dimensions to conceptually understand them.
- Create a sheet of formulae that includes all vectors, projectiles equations and relations of circular motion so that you can revise it quickly.
Importance of Class 11 Physics Chapter 3 Motion in a Plane
Class 11 Physics Chapter 3 Motion in a Plane is important because it provides a good foundation to the real life two dimensional motion like the movement of a ball or a rocket. The chapter brings in the usage of vectors to study quantities that have magnitude and direction which is fundamental to problem-solving in Physics. The clear understanding of these concepts aids the students in the CBSE exams as well as competitive exams such as JEE and NEET.
Prepares Physics on Higher Level
- Class 11 Notes on Motion in a Plane The Class 11 Notes on Motion in a Plane are important because they expose students to the concepts of vector algebra, projectile motion, and circular motion, which are crucial in Class 12 Physics and in competitive examinations such as JEE and NEET.
Simplifies Vector Concepts
- Those notes enable the students to learn the addition and subtraction of vectors and the resolution of vectors, and it becomes simpler to resolve the problems of forces, velocity, and acceleration in two dimensions in the real-life applications of physics.
Increases Problem-Solving
- Class 11 Motion in a Plane notes with clear derivations and solved examples enhance students' capacity to solve numeric problems related to the concepts of kinematics, which is a subject of regular study in the CBSE board exams.
Beneficial in Competitive Exams
- Motion in a Plane is a heavyweight subject in exams such as JEE Main, JEE Advanced, NEET, and other engineering/medical entrances, and it is thus essential to have such notes to revise within the shortest time possible.
Enhances Practical Applications
- The chapter is directly implemented in the real world, such as the projectile motion of a ball, the motion of satellites, and the circular motion of vehicles, where students get an idea of practical physics.
Saves Time During Revision
- Properly laid out Class 11 Physics Motion in a Plane notes will give a brief overview of formulae, graphs and important points to save time when it will be time to revise the exam in the last minute.
How to Use NCERT Class 11 Physics Chapter 3 Notes Effectively?
NCERT notes Class 11 Physics Chapter 3 Motion in a Plane present a rather brief and understandable explanation of the two-dimensional motion through vectors and their applications. In order to achieve the best outcome, students are not supposed to read the Motion in a Plane Class 11 Physics notes passively but they are supposed to be actively involved with the notes. This would guarantee better knowledge, improved memory, and precision in problem-solving in the exams.
- Visualize Concepts - Visualize concepts through drawing of vector diagrams, velocity triangles and motion graphs and taking of notes to enhance the visualization skills.
- Concentrate on Derivations - Determine the derivations, such as projectile motion equations, step by step with the help of notes and do not memorise.
- Concept Mapping - Draw flowcharts among displacement, velocity, acceleration, and the components of vectors to use without difficulty.
- Practice - In the course of solving problems, be sure to record frequent errors (e.g. the incorrect use of angles in solving equations) and compare with notes.
- Timed Practice - Solve some of the numerical problems with the notes within a timed format, or as if you were in an exam.
- Peer Learning - Share your thoughts on the concepts of the relative motion and vector addition in your notes with your peers to answer any uncertainties.
- Connection of Chapters - These notes will give you a view of the connections between the next chapters such as Laws of Motion and Work, Energy and Power.
NCERT Class 12 Notes Chapter-Wise
Preparing for Class 12 board exams becomes easier with NCERT Class 12 Notes (Chapter-wise). These notes provide clear explanations, important formulas, and key concepts for every subject, making revision quick and effective. Students can access chapter-wise NCERT notes with links to strengthen their preparation for CBSE exams as well as competitive exams like JEE and NEET.
Subject-Wise NCERT Exemplar Solutions
- NCERT Exemplar Class 11 Solutions
- NCERT Exemplar Class 11 Maths
- NCERT Exemplar Class 11 Physics
- NCERT Exemplar Class 11 Chemistry
- NCERT Exemplar Class 11 Biology
Subject-Wise NCERT Solutions
NCERT Books and Syllabus
Frequently Asked Questions (FAQs)
The main difference is in their point of reference. An object's location with regard to a fixed origin is specified by a position vector (point P is at vector r from the origin, for example). A displacement vector, on the other hand, shows the shift in position. Regardless of the origin, it is a straight line traced from an object's starting point to its final point.
A bird turning mid-air, a car taking a curved turn, or a football following a curved path after a kick all show motion in two dimensions, which this chapter helps you understand.
The basic concepts of "Motion in a Straight Line" serve as the foundation for "Motion in a Plane." The horizontal and vertical components of motion are addressed separately by the three primary equations of motion. These formulas are used to describe the vertical motion of projectiles (a = g) and simplified for the horizontal motion (a = 0).
It explains how objects move in two dimensions using vectors. You'll learn about projectile motion, circular motion, and how to handle direction and magnitude together.
The following statement is correct: "A displacement vector is a location vector." In class 11th physics chapter 4 notes the position or condition of any point that is similar to the position vector is represented by a displacement vector. To some extent, the position and displacement vectors are comparable. The displacement vector differs from the position vector in that it describes the position of any point in relation to other points rather than the origin. The position vector, on the other hand, specifies the position of any point in relation to the origin. This is how the truth of the statement is demonstrated.
A unit vector is a vector with a magnitude of 1, commonly denoted by a hat symbol (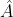 ), used to represent direction without affecting magnitude
), used to represent direction without affecting magnitude
Yes, Motion in a Plane Class 11 notes are useful for JEE (Joint Entrance Examination) preparation. These notes cover essential concepts from the CBSE Physics Syllabus and can serve as a valuable resource for understanding and revising key topics related to motion in a plane. JEE often includes questions that require a strong foundation in physics, and having comprehensive notes can aid in effective preparation for the examination.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
