NCERT Class 11 Physics Chapter 11 Notes Thermal Properties of Matter - Download PDF

NCERT Notes for Class 11 Physics Chapter 10: Download PDF

These Thermal Properties of Matter Class 11 Notes are easy and quick to revise, and provide step-by-step explanations, key formulas, and solved problems. The PDF is free to download, and the students can study it anywhere and at any time to sharpen their knowledge and gain enough confidence to have a successful experience at the board exams, JEE and NEET. The notes are useful to facilitate the conceptualisation, training in the practical mathematical tasks, as well as reviewing effectively.

Download PDF

NCERT Notes for Class 11 Physics Chapter 10

These Thermal Properties of Matter Class 11 Notes are a concise and clear summary of all the significant concepts, formulas and solved examples. They will be ready to make students learn the thermal properties of matter with ease and have a revision with ease. These notes are perfect in the preparation of board exams, JEE, and NEET and help to learn at a faster and more efficient rate.

Temperature and Heat

Temperature is the measurement of a body's degree of hotness or coolness.
Example:- A cup of hot soup or an ice cream scoop

Heat is a kind of energy that is exchanged via the temperature difference between two (or more) systems or between a system and its surroundings.
For example, a cup of hot coffee might be regarded as an object or system, whereas everything else is the environment.

As a result of the temperature difference, heat will move from one thing to another.

The SI unit of Heat is the joule.

Measurement of Temperature

A thermometer is used to determine the temperature.
In liquid-in-glass thermometers, mercury and alcohol are regularly used liquids.
The following graph depicts the relationship between temperature in Celsius and Fahrenheit graphically:-

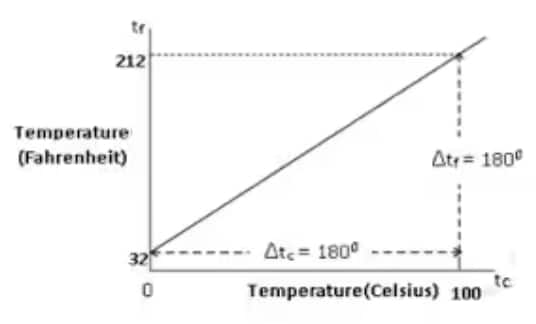
$\left(t_{\mathrm{f}}-32\right) / 180=t_{\mathrm{c}} / 100$

Where t_f means Fahrenheit temperature

t_c means Celsius temperature

Absolute Temperature and the Ideal Gas Equation

A thermometer that employs any gas, on the other hand, will produce the same readings regardless of the gas used since all gases expand at the same rate at low temperatures.

The following variables are used to characterise the behaviour of gas:

• Quantity(mass)

• Pressure

• Volume

• Temperature

Gases with a low density obey the following rules: -

1. Boyle’s Law– In this law, the product of PV = constant(when temperature T is constant)

2. Charles’ Law- In this law, the ratio of V/T = constant (when pressure P is constant)

When both of the preceding principles are combined, the equation becomes PV = RT, where R stands for the universal gas constant.

Absolute Zero

The minimal absolute temperature of an ideal gas is defined as Absolute Zero.
We get a straight line if we plot pressure versus temperature and then extend the line backwards to the x-axis, as seen in the graph below.

The lowest temperature measured (experimentally) was -273.15 °C, which is known as absolute zero.

The relationship between temperature in Kelvin and temperature in Celsius is provided by

$\mathbf{T}=\mathbf{t}_c+273.15$

Thermal Expansion

Thermal expansion is the phenomenon of a body's dimensions expanding as its temperature rises.

Thermal Expansion Types

Expansion in length is known as linear expansion.

Expansion in the area is known as area expansion.

Volume Expansion: This is a term that refers to the increase in volume of anything.

Linear Expansion

The term "linear expansion" refers to the length of anything expanding as the temperature rises.

The term "linear expansion" refers to a fractional change in length or how the length changes in relation to the original length.

$\Delta L / L=\alpha_L \Delta T$

ΔL is the length change, L is the initial length, ΔT is the temperature change, and αL is the linear coefficient of thermal expansion.

Area Expansion

The term "area expansion" refers to the expansion of an area as a result of an increase in temperature.

There is an increase in both length and width when an area is expanded.

$\Delta \mathbf{A} / \mathbf{A}=\alpha_{\mathrm{a}} \Delta \mathbf{T}$

Where αa = coefficient of area expansion.

Volume Expansion

It is defined as the expansion of volume as a result of an increase in temperature.

This indicates that a substance's length, width, and height have increased.

$\Delta V / V=\alpha_v \Delta T$

Where αv = coefficient of volume expansion.

Anomalous Behaviour of Water

At 4 °C, water has the highest density.

When the temperature drops below 4 °C, the water expands, and the density falls.

Because of this feature, water in lakes and ponds only freezes at the top layer and not at the bottom, but if the water freezes at the bottom as well, animal and plant life would be unable to survive.

Specific heat capacity:

Heat Capacity

A quantity termed the heat capacity of a substance characterises the change in temperature of a substance when a particular amount of heat is absorbed or rejected by that substance.

$S=\Delta Q / \Delta T$

Where ΔQ is the amount of heat supplied to the substance and ΔT change in its temperature.

Specific heat is the amount of heat received or rejected per unit mass by a substance to change its temperature by one degree.

$\mathbf{s}=\mathbf{S} / \mathbf{m}$

Molar specific heat capacity: -

The heat capacity per mole is the amount of heat (in moles) absorbed or rejected by a substance to change its temperature by one unit.

$C=S / \mu=\Delta Q / \mu \Delta T$

The molar specific heat capacity (C_p) is defined as follows:

The equivalent molar specific heat capacity at constant pressure is called molar specific heat capacity at constant pressure if the gas is retained at constant pressure during the heat transfer (C_p).

Molar specific heat capacity (C_v):-

The equivalent molar specific heat capacity at constant volume is called molar specific heat capacity at constant volume if the volume of the gas is maintained during the heat transfer (C_v).

Calorimetry

The word calorimetry comes from two parts:

• Calorie, which means "heat"

• Metry, which means "measuring"

So, calorimetry is the process of measuring heat.

It involves the transfer of heat from a hotter body to a cooler body, while making sure that no heat is lost to the surroundings.

The basic idea behind calorimetry is that the heat lost by one body is equal to the heat gained by another. The device used to measure this heat transfer is called a calorimeter.

Change of State

A change of state is when a substance transitions from one form (solid, liquid, or gas) to another. For example:

• Melting is when a solid (like ice) turns into a liquid (like water).

• Fusion is the process by which a liquid (like water) turns into a solid (like ice).

Thermal Equilibrium

In thermal equilibrium, there’s no heat gain or loss. The melting point of a substance is the temperature at which its solid and liquid states are in balance (equilibrium).

• Normal Melting Point: This is the temperature at which a substance melts under standard atmospheric pressure.

Regelation

Regelation is the process where pressure lowers the freezing point of water, allowing ice to melt under pressure and refreeze when the pressure is reduced.

Vaporization

Vaporisation is the process by which a liquid changes into a gas (for example, water turning into steam).

Sublimation

Sublimation is when a solid directly turns into a gas without becoming a liquid first. During sublimation, both the solid and gas forms exist in thermal equilibrium.

Latent Heat

Latent heat is the amount of heat energy required to change the state of a substance without changing its temperature. For example, during melting or boiling, a substance absorbs or releases heat, but its temperature stays constant. There are two main types: latent heat of fusion (solid to liquid) and latent heat of vaporisation (liquid to gas). This concept helps explain why ice melts or water boils at specific temperatures.

Heat Transfer

Heat transfer refers to the process by which thermal energy moves from a body at a higher temperature to one at a lower temperature. This transfer can occur in three primary ways:

• Conduction – Transfer of heat through direct contact, mainly in solids. For example, a metal rod gets hot when one end is placed in a flame.
• Convection – Transfer of heat through the movement of fluids (liquids or gases). Warm fluids rise and cooler fluids sink, creating a convection current. For instance, boiling water in a pot.
• Radiation – Transfer of heat without a medium, in the form of electromagnetic waves. This is how the Sun heats the Earth.

Newton's Law of Cooling

Newton's Law of Cooling states that the rate at which a hot object cools down is directly proportional to the difference in temperature between the object and its surroundings, provided this difference is small. In simple words, the hotter the object compared to its surroundings, the faster it loses heat.

$
\frac{d T}{d t}=-k\left(T-T_{\text {surrounding }}\right)
$

Where:

• $\frac{d T}{d t}$ is the rate of change of temperature,
• $T$ is the temperature of the object,
• $T_{\text {surrounding }}$ is the surrounding temperature,
• $k$ is a constant depending on the nature of the object and its surroundings.

Class 11 Physics Chapter 10 Thermal Properties of Matter: Previous Year Questions and Answers

Q1: Water falls from a height of 200 m into a pool. Calculate the rise in temperature of the water, assuming no heat dissipation from the water in the pool.
(Take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$, specific heat of water $=4200 \mathrm{~J} /(\mathrm{kg} \mathrm{K})$ )

Answer:

Setting the potential energy loss equal to the heat gained:

$\begin{aligned} & m g h=m s \Delta T \\ & \Delta T=\frac{g h}{S}=\frac{10 \times 200}{4200}=0.48 \mathrm{~K}\end{aligned}$

Q2:

Two cylindrical rods A and B made of different materials, are joined in a straight line. The ratio of lengths, radii and thermal conductivities of these rods are : $\frac{L_A}{L_B}=\frac{1}{2}, \frac{r_A}{r_B}=2$ and $\frac{\mathrm{K}_A}{K_B}=\frac{1}{2}$. The free ends of rods A and B are maintained at $400 \mathrm{~K}, 200 \mathrm{~K}$, respectively. The temperature of rods interface is _____ K , when equilibrium is established.

Answer:

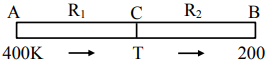
$\begin{aligned} & \mathrm{R}_1=\frac{\ell_1}{\mathrm{~K}_1 \mathrm{~A}_1}, \mathrm{R}_2=\frac{\ell_2}{\mathrm{~K}_2 \mathrm{~A}_2} \\ & \frac{\mathrm{dQ}}{\mathrm{dt}}=\frac{\Delta \mathrm{T}}{\mathrm{R}} \\ & \left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right)_1=\left(\frac{\mathrm{dQ}}{dt}\right)_2 \\ & \frac{400-T}{R_1}=\frac{T-200}{R_2} \\ & \frac{400-\mathrm{T}}{\mathrm{T}-200}=\frac{\mathrm{R}_1}{\mathrm{R}_2}=\left(\frac{\ell_1}{\ell_2}\right)\left(\frac{\mathrm{r}_2}{\mathrm{r}_1}\right)^2 \times \frac{\mathrm{K}_2}{\mathrm{~K}_1} =\frac{1}{2} \times\left(\frac{1}{2}\right)^2 \times 2 =\left(\frac{1}{4}\right) \\ & \frac{400-\mathrm{T}}{\mathrm{T}-200}=\frac{1}{4} \\ & 1600-4 \mathrm{~T}=\mathrm{T}-200 \\ & 5 \mathrm{~T}=1800 \\ & \mathrm{~T}=360 \mathrm{~K}\end{aligned}$

Hence, the answer is 360.

Q3:

Consider a rectangular sheet of solid material of length $/=9 \mathrm{~cm}$ and width $d=4 \mathrm{~cm}$. The coefficient of linear expansion is $\alpha=3.1 \times 10^{-5} \mathrm{~K}^{-1}$ at room temperature and one atmospheric pressure. The mass of sheet $m=0.1 \mathrm{~kg}$ and the specific heat capacity $C_v=900 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}$. If the amount of heat supplied to the material is $8.1 \times 10^2 \mathrm{~J}$ then change in area of the rectangular sheet is

Answer:

$\begin{aligned} & Q=m c \Delta T \\ & 8.1 \times 10^2=900 \times 0.1 \times \Delta T \\ & \Delta T=9 \mathrm{~K} \\ & \Delta A=A \cdot 2 \propto \Delta T \\ & =36 \times 2 \times 3.1 \times 10^{-5} \times 9 \times 10^{-4} \\ & =2 \times 10^{-6} \mathrm{~m}^2\end{aligned}$

Importance of Thermal properties of fluids Class 11 Notes

Thermal Properties of Matter Class 11 Notes are necessary to create a solid conceptual base. They assist the students to understand the major subjects, such as the transfer of heat, thermal expansion, and specific heat in a simple and fast manner. The notes are especially handy when revising, taking board exams, and competitive exams such as JEE and NEET.

• Understanding Heat Transfer Mechanisms - In the notes, the concepts of conduction, convection, and radiation have been explained. Students will be able to relate these concepts with the real life examples such as the reasons cooking vessels heat, formation of the sea breezes and the transfer of energy of the Sun to the planet.
• Applications in Thermal Expansion: These notes discuss the thermal expansion of solids, liquids, and gases. Real-world examples like expansion joints in bridges, bimetallic strips in thermostats, and separations in the railway lines are described, and thus, concept learning becomes simpler.
• Specific and Latent Heat Calculations: There are formulae and derivations in the notes that allow one to easily calculate the amount of heat taken in or given out by a substance. This makes it effective in solving numerical problems on temperature change, phase change and heat energy.
• Newton's Law of Cooling: The notes elaborate on how objects cool down over time, with derivations and example problems. This can be connected to the real life situations such as the cooling of hot tea by students and this helps them to develop reasoning and problem solving abilities.
• Association with Real-Life Applications: The concepts are easy to memorize and understand as the notes connect the theory with the real world applications such as mercury expansion in thermometers, ice melting, and thermal insulation.
• Exam-Oriented revision tool: These notes are a collection of all vital points, formulae, and plans, and thus, it is useful in both board exams preparation (CBSE Class 11) and also in competitive exams such as JEE Main, NEET, and Olympiads.
• Problem-Solving Practice: Solved problems and step-by-step directions to the common numerical problems enhance the intellectual clarity and enhance the confidence in approaching both theoretical and practical questions.
• Quick Prep in Case of Last-minute Revision: Clearly organised points, formulae highlights as well as diagrams enable quick revision prior to the exams without missing the vital concepts.

NCERT Class 12 Notes Chapter-Wise

These NCERT Class 12 Physics notes provide a structured and comprehensive way to revise all chapters efficiently. Designed by subject experts, the notes simplify complex concepts, include important formulas, solved examples, and key points, making them ideal for quick revision. Students can access chapter-wise links to download PDFs, helping them study anytime and anywhere, whether for board exams or competitive exams like JEE and NEET.

Subject Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject Wise NCERT Solutions

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus