Q1(a) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.

Answer:

In this case, the direction of force and displacement are the same, this work done is positive.

Q1(b) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: work done by gravitational force in the above case

Answer:

In this case, the direction of displacement is upward and the direction of force is downward. Thus work done is negative in nature.

Q1 (c) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: work done by friction on a body sliding down an inclined plane,

Answer:

We know that friction acts in the direction opposite to the direction of motion. Hence work done by the frictional force is negative.

Q 1 (d) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: work done by an applied force on a body moving on a rough horizontal plane with uniform velocity

Answer:

In this case, the applied force supports the motion of the object (balances frictional force). Thus work done by the force is positive.

Q1 (e) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: work done by the resistive force of air on a vibrating pendulum in bringing it to rest.

Answer:

Work done in this case is negative as the direction of force and motion are not identical.

Q2 (a) A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the work done by the applied force in 10 s,

Answer:

Using Newton's law we can write :

$\begin{aligned}
a & =\frac{F}{m} \\
& =\frac{7}{2}=3.5 \mathrm{~m} / \mathrm{s}^2
\end{aligned}$

The frictional force is given by :

$\begin{aligned}
f & =\mu m g \\
& =0.1 \times 2 \times 9.8=1.96 \mathrm{~N}
\end{aligned}$

Its direction will be opposite of the direction of the motion. Thus acceleration produced will be negative.

$a=\frac{-1.96}{2}=-0.98 \mathrm{~m} / \mathrm{s}^2$

Thus the net acceleration is $=3.5-0.98=2.52 \mathrm{~m} / \mathrm{s}^2$.
The total distance travelled is given by :
or

$\begin{aligned}
s & =u t+\frac{1}{2} a t^2 \\
& =0+\frac{1}{2}(2.52) 10^2=126 \mathrm{~m}
\end{aligned}$

Hence the work done by applied force is given by :

$W=F . s=7 \times 126=882 \mathrm{~J}$

Q2 (b) A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the work done by friction in 10 s,

Answer:

The work done by frictional force will be negative as the force opposes the motion.

W = f.s = −1.96×126 = −247 J

Q2 (c) A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the work done by the net force on the body in 10 s,

Answer:

The net work done will be the sum of work done by applied force and work done by frictional force.

W = 882 − 247 = 635 J

Q2 (d) A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the change in kinetic energy of the body in 10 s

Answer:

It is given that initial velocity is zero. The final velocity can be calculated by the equation of motion:

$\begin{aligned}
v & =u+a t \\
& =0+(2.52) 10 \\
& =25.2 \mathrm{~m} / \mathrm{s}
\end{aligned}$

Thus change is kinetic energy is :

$\begin{aligned}
\Delta K & =\frac{1}{2} m v^2-\frac{1}{2} m u^2 \\
& =\frac{1}{2} \times 2(25.2)^2-0 \\
& =635 \mathrm{~J}
\end{aligned}$

Q3 Given in Fig are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

Answer:

Total energy = kinetic energy (KE) + potential energy(PE)

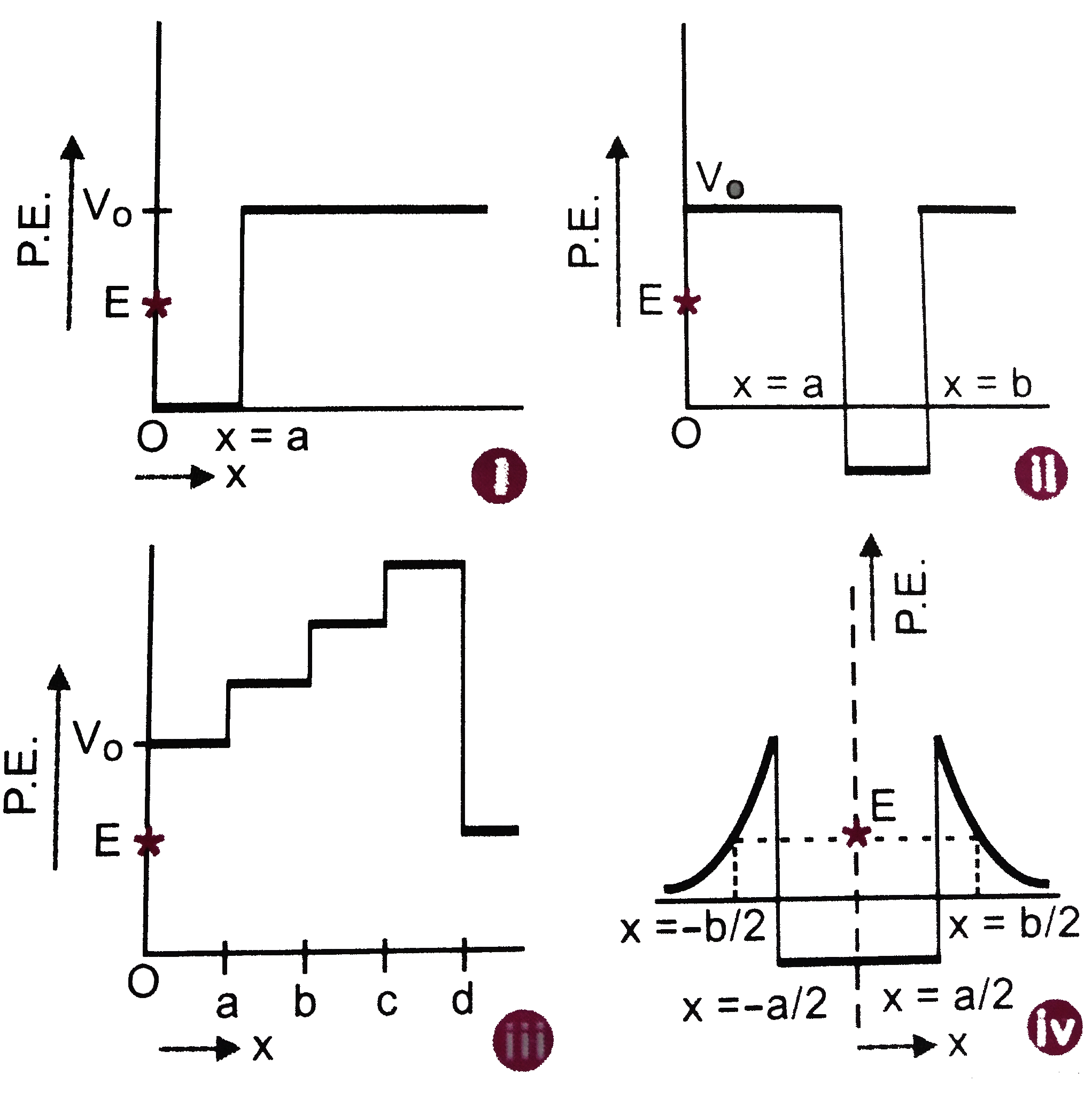
KE > 0 since m and v² is positive. If KE <0, particles cannot be find. If PE>TE, then KE<0 (now in all graph, check for this condition)

In case 1: kinetic energy is negative for x<a. So at x<a particle cannot be found.

In case 2: for x<a and for x> b, kinetic energy is negative. So the particle cannot be found in these regions.

In the third case, the minimum potential energy is when a<x<b. At this position, the potential energy is negative (- U₁ ).

The kinetic energy in this case is given by :

K.E. = E − (−U₁) = E + U₁

And the minimum energy of particle is - U₁ .

In the fourth case, the particle will not exist in the states which will have potential energy greater than the total energy.

Thus, the particle will not exist in −b₂<x<b₂ and −a₂<x<a₂.

The minimum energy of the particle will be - U₁ as it is the minimum potential energy.

Q4 The potential energy function for a particle executing linear simple harmonic motion is given by V(x)=kx²/2 , where k is the force constant of the oscillator. For k=0.5Nm⁻¹ the graph of V(x) versus x is shown in Fig. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x=±2

Answer:

The total energy of the particle is given by :

$\begin{aligned}
E & =K \cdot E+P \cdot E \\
& =\frac{1}{2} m v^2+\frac{1}{2} k x^2
\end{aligned}$

At the extreme position, the object's velocity is zero; thus, its kinetic energy at that point is zero.

$\begin{aligned}
& E=\frac{1}{2} k x^2 \\
& 1=\frac{1}{2}(0.5) x^2
\end{aligned}$
$x^2=4$
$x= \pm 2$

Hence, the extreme position is $\pm 2 \mathrm{~m}$.

Q5 (a) Answer the following :
The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?

Answer:

The total energy is given by :

E = K.E + P.E

or E = $\frac{1}{2} m v^2 + mgh$

The burning of casing results in a reduction in the mass of the rocket. This leads to a lowering of the total energy.

Thus, the heat required for burning is obtained from the expenses of the rocket.

Q5 (b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?

Answer:

This is because the gravitational force is a conservative force. And we know that the work done by a conservative force in a closed path is always zero. That's why the work done by the gravitational force is zero in a complete orbit revolution.

Q5 (c) An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the Earth?

Answer:

The total energy of an artificial satellite remains constant. Thus, when it approaches the Earth, the distance between them decreases. This results in a decrease in the potential energy of the satellite. By energy conservation, the kinetic energy of the satellite increases, and so does the velocity.

Q5 (d) In Fig.(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig.(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?

Answer:

In the first case,

Work done is :

W = F.s = Fscos⁡Θ

or W = mgscos⁡Θ

or W = 15×9.8×2×cos⁡90^∘

or W = 0

In the second case :

W = Fscos⁡Θ

or W = mgscos⁡0^∘

or W = 15×9.8×2 = 294 J

Thus work done in the second case is greater than the first case.

Q6 (a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.

Answer:

It is given that work done by the conservative force is positive, thus the force acts in the direction of the motion. This results in a decrease in distance between the bodies. Thus it's potential energy decreases .

Q6 (b) Work done by a body against friction always results in a loss of its kinetic/potential energy.

Answer:

Work done by the body against friction results in a decrease in the velocity of the body. Thus the kinetic energy of the body decreases.

Q6 (c) The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.

Answer:

The internal force cannot produce a change in the total momentum as no external force is acting. Thus the change in total momentum is proportional to the external forces acting on the body.

Q6(d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.

Answer:

The conservation of total linear momentum doesn't depend upon the fact whether it is an elastic collision or an inelastic collision.

Q7(a) State if each of the following statements is true or false. Give reasons for your answer.

In an elastic collision of two bodies, the momentum and energy of each body is conserved.

Answer:

False: - The linear momentum and energy will be conserved if both are considered in a system. But for individual bodies, this conservation of momentum and energy doesn't hold. This is because the impact during the collision may transfer energy/momentum of one ball to the other ball.

Q7 (b) State if each of the following statements is true or false. Give reasons for your answer.

Total energy of a system is always conserved, no matter what internal and external forces on the body are present.

Answer:

False: - Internal forces will not change the energy of the system but external forces can change the total energy by changing their magnitude or direction.

Q7 (c) State if each of the following statements is true or false. Give reasons for your answer.

Work done in the motion of a body over a closed loop is zero for every force in nature.

Answer:

False:- This is true only for conservative forces e.g. gravitational force. For e.g in case of frictional force (non-conservative force), the work done in a closed-loop cannot be zero as energy is wasted throughout.

Q7 (d) State if each of the following statements is true or false. Give reasons for your answer.

In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.

Answer:

True but not always:- In the case of inelastic collisions, few amounts of energy is converted into other forms of energy such as sound or in deformation. Thus final kinetic energy is always less as compared to initial kinetic energy. But in case of the explosion of a bomb final kinetic energy is greater than the initial kinetic energy

Q8 (a) Answer carefully, with reasons: In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?

Answer:

No, because at the time of the collision, the kinetic energy is converted to the potential energy. Thus total kinetic energy is not constant at the collision.

Q8 (b) Is the total linear momentum conserved during the short time of an elastic collision of two balls?

Answer:

Yes, in case of elastic collision the total linear momentum of the system remains conserved as no external force is acting on the system of balls.

Q8 (c) What are the answers to (a) and (b) for an inelastic collision?

Answer:

The total kinetic energy of the system cannot be conserved in case of inelastic collision as there is loss of energy in the form of deformation. But the total linear momentum of the system remains constant even in the case of inelastic collision as no external force is acting.

Q8 (d) If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational\potential energy).

Answer:

Since the potential energy of the system depends upon the separation between the bodies thus the forces acting on the body are conservative in nature. We know that conservative forces produce elastic collisions.

Q 9) A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to

(i)t^1/2

(ii)t

(iii)t^3/2

(iv)t²

Answer:

It is given that acceleration is constant thus force will also be constant (by Newton's law of motion F = ma).

Also,

a = dv/dt = constant

or dv = C dt

Thus v ∝ t

Now, the work done by the force is given by :

P = F.v

Hence power is directly proportional to the time.

Q10 A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to

$(i) t^{1 / 2}(i i) t(i i i) t^{3 / 2}(i v) t^2$

Answer:

We know that the power is given by:

$\begin{aligned}
P & =F \cdot v \\
& =m a \cdot v \\
& =m \frac{d v}{d t} v
\end{aligned}$

It is given that power is constant, thus :

$\begin{aligned}
m v \frac{d v}{d t} & =\text { constant } \\
v d v & =\frac{C}{m} d t
\end{aligned}$

By integrating both sides, we get

$v=\left(\sqrt{\frac{2 C t}{m}}\right)$

Also, we can write :

$\begin{aligned}
& v=\frac{d x}{d t} \\
& \frac{d x}{d t}=\sqrt{\frac{2 C}{m}} t^{\frac{1}{2}}
\end{aligned}$

By integrating we get the relation :

$x \propto t^{\frac{3}{2}}$

Q11 A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by $\vec{F}=-\hat{i}+2 \hat{j}+3 \hat{k} N$ where $\hat{i}, \hat{j}, \hat{k}$ are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis?

Answer:

Force is given to be :

$\vec{F}=-\hat{i}+2 \hat{j}+3 \hat{k} \ N$

And the displacement is :

$\vec{s}=4 \hat{k} \ m$

Thus the work done is given by :

$W$ =$\vec{F} \cdot \vec{s}$
$W =(-\hat{i}+2 \hat{j}+3 \hat{k}) \cdot(4 \hat{k}) \\$
$W =0+0-3(4)=12 \mathrm{~J}$

Q12 An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton? Obtain the ratio of their speeds. (electron mass $=9.11 \times 10^{-31} \mathrm{Kg}$, proton mass $1.67 \times 10^{-27} \mathrm{Kg}, 1 \mathrm{eV}=1.60 \times 10^{-19} \mathrm{~J}$)

Answer:

The kinetic energy of the electron is given by:

$\begin{gathered}
K_e=\frac{1}{2} m v_e^2 \\
1.6 \times 10^{-15} J=\frac{1}{2} \times 9.11 \times 10^{-31} \times v_e^2
\end{gathered}$

Thus velocity is obtained as:

$\begin{aligned}
v_e & =\sqrt{\frac{2 \times 1.6 \times 10^{-15}}{9.11 \times 10^{-31}}} \\
& =5.93 \times 10^7 \mathrm{~m} / \mathrm{s}
\end{aligned}$

Similarly, we can find the velocity of the proton :

$\begin{aligned}
K_p & =\frac{1}{2} m v_p^2 \\
1.6 \times 10^{-14} J & =\frac{1}{2} \times 1.67 \times 10^{-27} \times v_p^2
\end{aligned}$

Thus velocity is obtained as:

$\begin{aligned}
v_p & =\sqrt{\frac{2 \times 1.6 \times 10^{-14}}{1.67 \times 10^{-27}}} \\
& =4.38 \times 10^6 \mathrm{~m} / \mathrm{s}
\end{aligned}$

Thus the ratio of their velocities is:

$\frac{v_e}{v_p}=\frac{5.93 \times 10^7}{4.38 \times 10^6}=13.54$

Q13 A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 10ms⁻¹ ?

Answer:

The volume of the drop is:

$
V=\frac{4}{3} \pi r^3=\frac{4}{3} \times 3.14 \times\left(2 \times 10^{-3}\right)^3
$

Thus the mass of raindrop is :

$
\begin{aligned}
m & =\rho V \\
& =10^3 \times \frac{4}{3} \times 3.14 \times\left(2 \times 10^{-3}\right)^3 \mathrm{Kg}
\end{aligned}
$

Thus the work done is given by:

$
W =F . s \\$
$ \Rightarrow W=m g s \\$
$\Rightarrow W =10^3 \times \frac{4}{3} \times 3.14 \times\left(2 \times 10^{-3}\right)^3 \times 9.8 \times 250\\$

$\Rightarrow W =0.082 \mathrm{~J}$

Now the total energy at the peak point is :

$
\begin{aligned}
E_p=m g h+0 & =m g h \\
= & 10^3 \times \frac{4}{3} \times 3.14 \times\left(2 \times 10^{-3}\right)^3 \times 9.8 \times 500 \\
= & 0.146 \mathrm{~J}
\end{aligned}
$

And the energy at the ground is :

$
\begin{aligned}
E_b=0+\frac{1}{2} m v^2 & =\frac{1}{2} m v^2 \\
& =\frac{1}{2} \times 10^3 \times \frac{4}{3} \times 3.14 \times\left(2 \times 10^{-3}\right)^3 \times(10)^2 \\
& =1.67 \times 10^{-3} \mathrm{~J}
\end{aligned}
$

Thus work done by the resistive force is :

$
=1.67 \times 10^{-3} J-0.164 J=-0.162 J
$

Q14 A molecule in a gas container hits a horizontal wall with speed 200ms⁻¹ and angle 30^o with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?

Answer:

The momentum is conserved in the collision as no external force is acting on the system. In the given case the rebound velocity is the same as the initial velocity thus the kinetic energy of the molecule initially and finally are same. Hence this is an elastic collision.

Q15 A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m³ in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?

Answer:

Mass of the water is:

$
\begin{aligned}
m & =\rho V \\
& =30 \times 10^3 \mathrm{Kg}
\end{aligned}
$

Thus the output power is given by :

$
\begin{aligned}
\text { Power } & =\frac{\text { Work done }}{\text { Time }} \\
& =\frac{m g h}{t} \\
& =\frac{30 \times 10^3 \times 9.8 \times 40}{900} \\
& =13.067 \times 10^3 \mathrm{~W}
\end{aligned}
$

Also, we are given that efficiency is 30 per cent.

Thus the input power is :

$
\begin{aligned}
P_i & =\frac{13.067}{\frac{30}{100}} \times 10^3 \\
& =43.6 \mathrm{kW}
\end{aligned}
$

Q16 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following (Fig) is a possible result after collision?

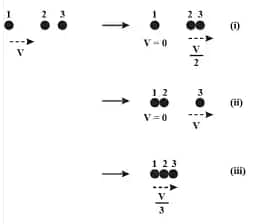
Answer:

The initial kinetic energy of the system is given by :

$
\begin{aligned}
& =\frac{1}{2} m v^2-\frac{1}{2} 2 m(0) \\
& =\frac{1}{2} m v^2
\end{aligned}
$

Case (i):-

The final kinetic energy is :$=\frac{1}{2} m \cdot 0-\frac{1}{2} 2 m\left(\frac{v}{2}\right)^2=\frac{1}{4} m v^2
$

Thus the kinetic energy is not conserved in this case.
Case (ii):-

The final kinetic energy is :$=\frac{1}{2} 2 m \cdot 0-\frac{1}{2} m v^2=\frac{1}{2} m v^2
$

Thus kinetic energy is conserved in this case.
Case (iii):-

The final kinetic energy is:-$=\frac{1}{2} \times 3 m \times\left(\frac{v}{3}\right)^2 \\ =\frac{1}{6} m v^2

$

Thus the kinetic energy is not conserved in this case.

Q17 The bob A of a pendulum released from 30^o to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 5.15. How high does the bob A rise after the collision? Neglect the size of
the bobs and assume the collision to be elastic.

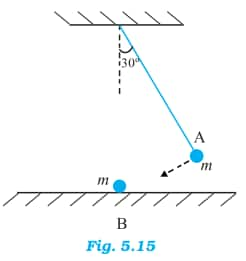
Answer:

This is an elastic collision thus the transfer of momentum will take place. It is given that bob B is at rest and bob A has some velocity. So in momentum transfer, bob B will gain the velocity in the left direction whereas bob A will come to rest (complete momentum transfer takes place).

Hence bob A will not rise.

Q18 The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?

Answer:

Consider the extreme position (horizontal) :-
The kinetic energy at this position is zero as velocity is zero.
Thus total energy is given by: $=m g l+0=m g l$
Now consider the mean position (lowermost point) :
Here the potential energy of Bob is zero.
Whereas kinetic energy is $
=\frac{1}{2} m v^2
$

Further, it is given that 5 per cent of energy is dissipated due to air resistance while coming down.
Thus energy equation becomes (conservation of energy):-

$
\frac{1}{2} m v^2=\frac{95}{100} \times m g l
$

or

$
v=\sqrt{\frac{2 \times 95 \times 1.5 \times 9.8}{100}}=5.28 \mathrm{~m} / \mathrm{s}
$

Q19 A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.005Kgs⁻¹ . What is the speed of the trolley after the entire sandbag is empty?

Answer:

Since the sand is falling in the trolley thus the force generated on the system (trolley and sandbag) is an internal force. There is no external force thus momentum of the system doesn't change. Hence speed remains the same i.e., 27 Km/hr.

Q20 A body of mass 0.5 kg travels in a straight line with velocity $v=ax^{3/2}$ where $a=5m^{−1/2}s^{−1}$ . What is the work done by the net force during its displacement from x = 0 to x = 2 m ?

Answer:

The relation between work done and the kinetic energy is given by :

$
\text { Work }=\frac{1}{2} m v^2-\frac{1}{2} m u^2
$

Using the relation $v=a x^{3 / 2}$ we can write :

$
\text { Initial velocity }=0 \quad(\text { at } x=0)
$

And the final velocity $=10 \sqrt{2} \mathrm{~m} / \mathrm{s} \quad($ at $\mathrm{x}=2)$.
Thus work done is :

$
\begin{aligned}
\text { Work } & =\frac{1}{2} m\left(v^2-u^2\right) \\
& =\frac{1}{2} \times 0.5 \times(10 \sqrt{2})^2 \\
& =50 \mathrm{~J}
\end{aligned}
$

Q21 (a) The blades of a windmill sweep out a circle of area A. If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t?

Answer:

The volume of wind = Av here A is the swept circle and v is the velocity.

Thus the mass of the wind is : - ρAv , ρ is the density of the air.

Hence mass of wind flowing through windmill in time t = ρAvt _.

Q21 (b) The blades of a windmill sweep out a circle of area A. What is the kinetic energy of the air?

Answer:

The kinetic energy is given by :

$
\begin{aligned}
& =\frac{1}{2} m v^2 \\
& =\frac{1}{2} \rho A v t v^2 \\
& =\frac{1}{2} \rho A t v^3
\end{aligned}
$

Thus the kinetic energy of wind is $\frac{1}{2} \rho A t v^3 \mathrm{~J}$.

Q21 (c) The blades of a windmill sweep out a circle of area A. Assume that the windmill converts 25% of the wind’s energy into electrical energy, and that A=30m²,v=36Km/h and the density of air is 1.2Kgm⁻³ What is the electrical power produced?

Answer:

It is given that 25 per cent of wind energy is converted into electrical energy.
Thus electric energy produced is :

$
\begin{aligned}
& =\frac{25}{100} \times \frac{1}{2} \rho A t v^3 \\
&= \frac{1}{8} \rho A t v^3
\end{aligned}
$

Now the electric power is given by :

$
\begin{aligned}
\text { Power } & =\frac{\text { Energy }}{\text { Time }} \\
& =\frac{\frac{1}{8} \rho A t v^3}{t}=\frac{1}{8} \rho A v^3 \\
& =\frac{1}{8} \times 1.2 \times 30 \times(10)^3 \\
& =4.5 \mathrm{kW}
\end{aligned}
$

Q22 (a) A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated. How much work does she do against the gravitational force?

Answer:

The work done against the gravitational force is given by :

= Number of times the weight is lifted × work done in 1 time.

= 1000×mgh

= 1000×10×9.8×0.5

= 49 kJ

Q22 (b) A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated. Fat supplies 3.8×10⁷J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?

Answer:

Efficiency is given to be 20 per cent.

Thus energy supplied by the person:

$
=\frac{20}{100} \times 3.8 \times 10^7
$

Thus the amount of fat lost is :

$
\begin{aligned}
& =\frac{49 \times 10^3}{\frac{20}{100} \times 3.8 \times 10^7} \\
& =6.45 \times 10^{-3} \mathrm{Kg}
\end{aligned}
$

Q23 (a) A family uses 8 kW of power. Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?

Answer:

It is given that the efficiency of energy conversion is 20 per cent.
According to question, we can write (equating power used by family) :

$
8 \times 10^3=\frac{20}{100} \times A \times 200
$

(Here A is the area required.)

$
A=\frac{8 \times 10^3}{40}
$

Thus required area is $200 \mathrm{~m}^2$.

Q23 (b) A family uses 8 kW of power. Compare this area to that of the roof of a typical house.

Answer:

A typical has dimensions of 14×14 m² .

The area of the roof of the house is 225 m² .

This is nearly equal to the area required for the production of the given amount of electricity