NCERT Solutions for Class 11 Physics Chapter 11 Thermodynamics
Have you ever asked yourself why it takes a long time to cool down a cup of hot tea or why the industrial revolution was run by steam engines? Such real-life phenomena were described in a clear and organised manner in the Thermodynamics Class 11 NCERT Solutions. The step-by-step solutions allow the students to learn about the transfer of energy, how heat can be converted into work, and how engines, refrigerators, and heat processes work.
This Story also Contains
- Class 11 Physics Chapter 11 - Thermodynamics: Download Solution PDF
- Thermodynamics NCERT Solutions: Exercise Questions
- Thermodynamics NCERT Solutions: Higher Order Thinking Skills (HOTS) Questions
- Class 11 Physics Chapter 11 - Thermodynamics: Topics
- Class 11 Physics Chapter 11 - Thermodynamics: Important Formulae
- Approach to Solve Questions of Class 11 Physics Chapter 11 - Thermodynamics
- How Can NCERT Solutions for Class 11 Physics Chapter 11 Help in Exam Preparation?
- What Extra Should Students Study Beyond NCERT for JEE/NEET?
- NCERT Solutions for Class 11 Physics Chapter Wise
- Importance of NCERT Solutions for Class 11 Physics Chapter 11 Thermodynamics
These NCERT Solutions for Class 11 Physics Chapter 11 - Thermodynamics, as prepared by experts in the subject, according to the latest syllabus of CBSE Class 11 Physics, simplify difficult concepts, and they are easier to revise and remember. They are extremely helpful in school and board exams as well as in competitive exams such as JEE and NEET, in which a clear understanding of concepts and problem-solving skills is decisive. Through the NCERT solutions, students will be able to enhance their mastery of the laws of thermodynamics, energy conservation and power engines, as well as increase logic and confidence in exams. By using these elaborate NCERT Solutions for Class 11 Physics Chapter 11 - Thermodynamics, one will be able to master Thermodynamics with a lot of interest and concentrate on the exam.
Class 11 Physics Chapter 11 - Thermodynamics: Download Solution PDF
The Class 11 Physics Chapter 11 - Thermodynamics question answers give well-elaborated and step-wise Solutions to all questions in the textbook, thereby enabling the student to solidify his/her knowledge of the specific subject. The best part about this class 11 physics chapter 11 Thermodynamics questions answers is that it is better suited when preparing to write exams, and it is in the form of an easy-to-download PDF file that can be revised quickly and at any time it is required.
Thermodynamics NCERT Solutions: Exercise Questions
The Thermodynamics class 11 question answers are step-by-step explanations of the exercise questions, and this makes the complex ideas easier to assimilate. These class 11 physics chapter 11 Thermodynamics questions answers equip students with the skills to master concepts such as heat, work, internal energy and the laws of thermodynamics to help them adequately prepare to face both the board examination and competitive examinations like JEE and NEET.
Answer:
The volumetric flow of water is
$\\\frac{dV}{dt}=3\ litres\ minute^{-1}\\$
Density of water = 1000 g/litre
The mass flow rate of water is
$\\\frac{dm}{dt}=\rho \frac{dV}{dt}\\ $
$\frac{dm}{dt}=3000\ g\ min^{-1}$
Specific heat of water, c = 4.2 J g-1 oC-1
The rise in temperature is $\Delta T=77-27=50\ ^{o}C$
The rate of energy consumption will be
$\\\frac{dQ}{dt}=\frac{dm}{dt}c\Delta T\\ $
$\frac{dQ}{dt}=3000\times 4.2\times 50\\$
$ \frac{dQ}{dt}=6.3\times 10^{5}\ J\ min^{-1}$
The heat of combustion of fuel $=4.0\times 10^{4}J/g$
The rate of consumption of fuel is
$\\\frac{6.3\times 10^{5}}{4\times 10^{4}}\\ =15.75\ g\ min^{-1}$
Answer:
Mass of nitrogen, $m=2.0\times 10^{-2}kg=20g$
Molar Mass of nitrogen, MN = 28 g
The number of moles is n
$\\n=\frac{m}{M_{N}}\\$
$ n=\frac{20}{28}\\$
$ n=0.714$
As nitrogen is a diatomic gas, its molar specific heat at constant pressure, CP is as follows
$\\C_{P}=\frac{7R}{2}\\ $
$C_{P}=\frac{7\times 8.3}{2}\\$
$ C_{P}=29.05\ J\ mol^{-1}\ ^{o}C^{-1}$
Rise in temperature, $\\\Delta T=45 ^{o}C^{-1}$
The amount of heat Q that must be supplied is
$\\Q=nC_{P}\Delta T\\ $
$Q=0.714\times 29.05\times 45\\ $
$Q=933.38\ J$
Answer:
As we know, heat will flow from the hotter body to the colder body till their temperatures become equal. That temperature will be equal to the mean of the initial temperatures of the bodies only if the two thermal capacities of the two bodies are equal.
Answer:
The coolant should have a high specific heat so that it can absorb large amounts of heat without itself getting too hot, and its temperature lies in the permissible region. The higher the specific heat, the more heat will be absorbed by the same amount of material for a given increase in temperature.
Q11.3(c) Explain why air pressure in a car tyre increases during driving.
Answer:
As the car is driven, the air inside the tyre heats due to frictional forces. Thus, the temperature of the air inside the tyre increases and this, in turn, increases the pressure inside the tyre.
Answer:
The climate of a harbour town is more temperate than that of a town in a desert at the same latitude because of the formation of sea breezes.
Answer:
As the walls of the cylinder and the piston are insulated, the process will be adiabatic. i.e. $PV^{\gamma }$ would be constant.
Hydrogen is a diatomic gas and therefore $\gamma =1.4$
Let the initial and final pressures be P1 and P2, respectively.
Let the initial and final volumes be V1 and V2, respectively.
$\\P_{1}V_{1}^{\gamma }=P_{2}V_{2}^{\gamma }\\ $
$\frac{P_{2}}{P_{1}}=\left ( \frac{V_{1}}{V_{2}} \right )^{\gamma }\\ $
$\frac{P_{2}}{P_{1}}=2^{1.4}\\$
$ \frac{P_{2}}{P_{1}}=2.639$
The pressure thus increases by a factor of 2.639
Q11.5 In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a process in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case? (Take $1 cal = 4.19 J$ )
Answer:
In the first case, the process is adiabatic, i.e. $\Delta Q=0$
22.3 J work is done on the system, i.e. $\Delta W=-22.3\ J$
$\\\Delta Q=\Delta U+\Delta W$
$\\ 0=\Delta U-22.3\\ $
$\Delta U=22.3\ J$
Since in the latter process as well,l the initial and final states are the same as those in the former process, $\Delta U$ will remain the same for the latter case.
In the latter case, the net heat absorbed by the system is 9.35 cal
$\\\Delta Q=9.35\times 4.2\\$
$\Delta Q=39.3\ J$
$\\\Delta W=\Delta Q-\Delta U\\ $
$\Delta W=39.3-22.3\\ $
$\Delta W=17.0\ J$
The network done by the system in the latter case is 17.0 J
(a) What is the final pressure of the gas in A and B?
(b) What is the change in the internal energy of the gas?
(c) What is the change in the temperature of the gas?
Answer:
As the entire system is thermally insulated and as free expansion will be taking place, the temperature of the gas remains the same. Therefore, PV is constant.
Initial Pressure P1 = 1 atm
Initial Volume, V1 = V
Final Volume, V2 = 2V
Final Pressure P2 will be
$P_{2}=\frac{P_{1}V_{1}}{V_{2}}$
$ P_{2}=\frac{P_{1}}{2}$
$ P_{2}=0.5\ atm$
The final pressure of the gas in A and B is 0.5 atm.
b) Since the temperature of the gas does not change, its internal energy would also remain the same.
c) As the entire system is thermally insulated and as free expansion will be taking place, the temperature of the gas remains the same.
d) The intermediate states of the system do not lie on its P-V-T surface, as the process is a free expansion, it is rapid, and the intermediate states are non-equilibrium states.
Answer:
The rate at which heat is supplied $\Delta Q=100\ W$
The rate at which work is done $\Delta W=75\ J s^{-1}$
The rate of change of internal energy is $\\\Delta u$
$\begin{aligned}
\Delta U & =\Delta Q-\Delta W \\
\Delta U & =100-75 \\
\Delta U & =25 \mathrm{~J} \mathrm{~s}^{-1}
\end{aligned}$
The internal energy of the system is increasing at a rate of 25 J s-1
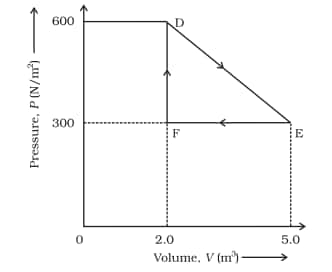
Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the total work done by the gas from D to E to F
Answer:
The work done by the gas as it goes from state D to E to F is equal to the area of triangle DEF
DF is change in pressure = 300 N m-2
FE is a change in Volume = 3 m3
$\\area(DEF)=\frac{1}{2}\times DF\times FE\\$
$area(DEF)=\frac{1}{2}\times300\times 3\\$
$area(DEF)=450\ J$
The work done is, therefore, 450 J.
Thermodynamics NCERT Solutions: Higher Order Thinking Skills (HOTS) Questions
The HOTS (Higher Order Thinking Skills) Questions for Class 11 Physics Chapter 11 - Thermodynamics are designed to push students beyond basic learning and encourage deeper conceptual understanding. These challenging problems strengthen analytical skills, logical reasoning, and application of thermodynamics principles, which are highly useful for JEE, NEET, and advanced exam preparation.
Q.1 Three moles of an ideal gas initially at a temperature $T_0=273 K$ were isothermally expanded to n = 5.0 times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. The total amount of heat transferred to the gas during the process equals Q = 80 kJ. Find the ratio $\gamma=C_P / C_V$ for this gas.
Answer:
$Q=Q_1+Q_2$
where
$Q_1 \Rightarrow$ for Isothermal process
$Q_2 \Rightarrow$ for Isochoric process
$Q=n^{\prime} \mathrm{R} T_0 \log \frac{n V_0}{V_0}+n^{\prime} C_V\left(T_C-T_B\right)$
As $T_C=n T_0 \quad$ (If volume is made n times)
$Q=n^{\prime} \mathrm{R} T_0 \log n+\gamma(n-1) T_0$
$\therefore \gamma=\left[1+\frac{n-1}{\frac{Q}{n^{\prime} R T_0}-\log n}\right]$
Putting the values
(Given n' = 3, n = 5)
$\gamma=1.4$
Hence, the answer is 1.4.
Q.2 In a pressure cooker, a sample of hydrogen gas was at a pressure of 1 atm. The volume of the cooker is 500 mL, and the mass of the cooker whistle is 100 g, and it has a cross-section area of $0.1\, cm^{2}$. Its initial temperature is 27°C. Select the correct option(s):
a) The final temperature of the gas if the gas can lift the whistle is 327°C
b) The final temperature of the gas if the gas can lift the whistle is 227°C
c) The pressure required to lift the whistle is $2\times 10^{5}$Pa
d) The pressure required to lift the whistle is $10^5$Pa
Answer:
The initial temperature of hydrogen, $T_1=273+27=300 \mathrm{~K}$
Initial pressure of hydrogen, $P_1=1 \mathrm{~atm}=10^5 \mathrm{~Pa}$
$
\begin{aligned}
& P_2=P_0+\frac{m g}{A} \\
& =10^5+\frac{100 \times 10^{-3}}{0.01 \times 10^{-4}} \\
& =2 \times 10^5
\end{aligned}
$
As the volume is constant, we can use Gay Lussac's law:
$
\frac{P_1}{T_1}=\frac{P_2}{T_2} \Rightarrow T_2=T_1 \times \frac{P_2}{P_1}=300 \times \frac{2}{1}=600 \mathrm{~K}=600-273=327^{\circ} \mathrm{C}
$
Hence, the answer is option (a),(c).
Q.3 The volume of a gas is compressed adiabatically from state $V_1=7 \mathrm{~m}^3$ at a pressure of $2. .4 \times 10^5 \mathrm{~N} \mathrm{~m}^{-2}$ to the volume $V_2=0.875 \mathrm{~m}^3$. If the same compression is performed isothermally, calculate the difference in work done (in $10^5$ joules) in both processes. It is given that $\gamma=$1.67.
Answer:
$
V_1=7 \mathrm{~m}^3, P_1=2.4 \times 10^5 \mathrm{Nm}^{-2}, V_2=0.875 \mathrm{~m}^3
$
In an adiabatic process
$
\begin{aligned}
& P_1 V_1^\gamma=P_2 V_2^\gamma \\
& \Rightarrow P_2=2.4 \times 10^5\left[\frac{7}{0.875}\right]^{1.6} \\
& \Rightarrow P_2=2.4 \times 10^5(8)^{\frac{5}{3}}=7.68 \times 10^6 \mathrm{~N} \mathrm{~m}^{-2}
\end{aligned}
$
Work done in an adiabatic process,
$
\begin{aligned}
& W=-\frac{P_2 V_2-P_1 V_1}{\gamma-1} \\
& W=-\frac{\left(7.68 \times 10^6 \times 0.875\right)-\left(2.4 \times 10^5 \times 7\right)}{1.67-1} \\
& W=-75.22 \times 10^5 \mathrm{~J}
\end{aligned}
$
Work done in the isothermal process,
$
\begin{aligned}
& W=2.3026 \mathrm{RT} \log \frac{V_2}{V_1}=2.3026 P_1 V_1 \log \frac{V_2}{V_1} \\
& =2.3026 \times 2.4 \times 10^5 \times 7 \times \log \left[\frac{0.875}{7.0}\right] \\
& =2.3026 \times 2.4 \times 10^5 \times 7 \log \left(\frac{1}{8}\right)=-34 \times 10^5 \mathrm{~J}
\end{aligned}
$
Difference in work done $=-75.22 \times 10^5 \mathrm{~J}+34 \times 10^5 \mathrm{~J}=-41.22 \times 10^5 \mathrm{~J}$
Q.4 1 mole of helium expands with temperature according to the relation $V=K T^{2 / 3}$. If the temperature changes by 60 K, find the heat absorbed (in J) by the monoatomic gas in the above process.
a) 1080.30
b) 1120.32
c) 1200
d) 1150.20
Answer:
$\begin{aligned} & V=K T^{2 / 3} \\ \Rightarrow & V=K\left(\frac{P V}{n R}\right)^{2 / 3} \\ \Rightarrow & P V^{-1 / 2}=\alpha \\ \because & C=C_V+\frac{R}{1-x}=\frac{3 R}{2}+\frac{R}{1+\frac{1}{2}}=\frac{13 R}{6} \\ Q & =n C \Delta T=1 \times \frac{13 R}{6} \times 60=130 R=1080.30 \mathrm{~J}\end{aligned}$
Hence, the answer is option (a).
Q.5. A diatomic ideal gas is heated at constant volume until the pressure is doubled and again heated at constant pressure until the volume is doubled. The average molar heat capacity for the whole process is $\frac{a}{b} R$. Find the remainder when $a$ is divided by $b$
Answer:
Let initial pressure, volume and temperature be $P_0, V_0, T_0$ indicated by state A in the P-V diagram. The gas is isochorically taken to state $B\left(2 P_0, V_0, 2 T_0\right)$ and then taken from state B to state $\mathrm{C}\left(2 P_0, 2 V_0, 4 T_0\right)$ isobarically.
Total heat absorbed by 1 mole of gas
$
\begin{aligned}
& \Delta Q=C_v\left(2 T_0-T_0\right)+C_P\left(4 T_0-2 T_0\right) \\
& =\frac{5}{2} R T_0+\frac{7}{2} R \times 2 T_0 \\
& =\frac{19}{2} R T_0
\end{aligned}
$
Total change in temperature from state A to C is: $\Delta T=3 T_0$
$\therefore$ Molar heat capacity $=\frac{\Delta Q}{\Delta T}=\frac{\frac{19}{2} R T_0}{3 T_0}=\frac{19}{6} R$
Hence, the answer is 1.
Class 11 Physics Chapter 11 - Thermodynamics: Topics
The NCERT Class 11 Physics Chapter 11 Thermodynamics Topics provide a structured breakdown of all key concepts covered in the chapter. Since the laws of thermodynamics apply to heat engines, refrigerators, and energy conservation, all concepts have been clearly explained to understand. Such topic-related information will assist the students in revising in a systematic manner and enhancing the preparation for board exams as well as competitive exams.
11.1 Introduction
11.2 Thermal Equilibrium
11.3 Zeroth Law Of Thermodynamics
11.4 Heat, Internal Energy And Work
11.5 First Law Of Thermodynamics
11.6 Specific Heat Capacity
11.7Thermodynamic State Variables And Equation Of State
11.8 Thermodynamic Processes
11.8.1 Quasi-Static Process
11.8.2 Isothermal Process
11.8.3 Adiabatic Process
11.8.4 Isochoric Process
11.8.5 Isobaric Process
11.8.6 Cyclic Process
11.9 Second Law Of Thermodynamics
11.10 Reversible And Irreversible Processes
11.11 Carnot Engine
Class 11 Physics Chapter 11 - Thermodynamics: Important Formulae
The Key Formulae in Class 11 Physics Chapter 11 - Thermodynamics serve as a quick revision guide to help solve the exercise questions and competitive examination problems. These formulas include relevant concepts such as heat, work, internal energy, and laws of thermodynamics, which students can use to enhance their ability to solve problems faster and accurately in exams such as JEE and NEET.<
1. First Law of Thermodynamics
$
\Delta Q=\Delta U+\Delta W
$
Where:
$\Delta Q=$ heat supplied to the system
$\Delta U=$ change in internal energy
$\Delta W=$ work done by the system
2. Work Done in an Isothermal Process
$
W=n R T \ln \left(\frac{V_f}{V_i}\right)
$
(For ideal gas, $T$ constant)
3. Work Done in Adiabatic Process
$
W=\frac{P_i V_i-P_f V_f}{\gamma-1}=\frac{n R\left(T_i-T_f\right)}{\gamma-1}
$
Where $\gamma=\frac{C_p}{C_v}$ (adiabatic index)
4. Adiabatic Relation for Ideal Gas
$P V^\gamma=\text { constant }$
5. Molar Specific Heats
For an ideal gas:
$
C_p-C_v=R
$
6. Internal Energy of an Ideal Gas
$
U=\frac{f}{2} n R T
$
Where $f=$ degrees of freedom
For monoatomic gas: $U=\frac{3}{2} n R T$
7. Heat Capacity
$
C=\frac{d Q}{d T}, \quad C=n C_m
$
Where $C_m=$ molar specific heat
9. Carnot Engine Efficiency
$
\eta=1-\frac{T_2}{T_1}
$
Where $T_1=$ temperature of source, $T_2=$ temperature of sink (in Kelvin)
Approach to Solve Questions of Class 11 Physics Chapter 11 - Thermodynamics
Solving questions from Class 11 Physics Chapter 11 - Thermodynamics requires a balance of conceptual clarity and practical application. Students should focus on understanding the laws of thermodynamics, interpreting heat, work, and internal energy relations, and applying formulas correctly. With a step-by-step approach, even complex numerical and reasoning-based questions become manageable and exam-ready.
- Begin with revising the fundamental laws of thermodynamics, like the zeroth, first, and second laws, as most questions you will get will be based on their applications and implications.
- You should learn the definitions of terms such as internal energy, heat, work, system, surroundings, and thermodynamic equilibrium to be able to recognise them in a numerical and conceptual question.
- Solve numerous problems related to heat exchange, work done in isothermal and adiabatic processes and efficiency of heat engines in order to understand the accuracy of problem solving.
- Draw and analyse PV diagrams since most of the questions require interpreting graphs or describing processes through the graphs provided.
- Try to have conceptual clarity about reversible and irreversible processes, and the difference between various thermodynamic systems, such as open, closed, and isolated systems.
- Connect the theory to real-life examples such as refrigerators and engines, since these practical applications will assist in remembering theories and answering reasoning questions well.
- Memorise all significant formulas and derivations on a regular basis, so that you can be able to remember them easily during exams.
How Can NCERT Solutions for Class 11 Physics Chapter 11 Help in Exam Preparation?
Thermodynamics class 11 question answers are extremely helpful for exam preparation as they simplify one of the most complex topics in physics. These Thermodynamics class 11 question answers explain complicated laws like the first and the second laws of thermodynamics in easy steps-by-step reasoning, and therefore, it is easy to understand the flow of energy, heat, and work in physical systems by the students. The answers to these questions will teach students how to use formulas properly when solving numerical problems involving isothermal and adiabatic processes. Important derivations and PV diagrams, and conceptual explanations are also part of the solution, strengthening problem-solving and analytical skills. In board exams or competitive exams such as JEE and NEET, these class 11 physics Thermodynamics question answers are used to teach students a variety of question patterns, like theoretical reasoning to numericals, so they can be conceptually clear and confident in exams. With the frequent revision with NCERT solutions, it is easy to memorise laws, definitions, and real-life applications to remember the same in the exam.
What Extra Should Students Study Beyond NCERT for JEE/NEET?
Although the foundation is made in NCERT Class 11 Physics Chapter 11 - Thermodynamics, the competitive examination, such as JEE and NEET, requires a deeper understanding and broader implementation of the concepts. Students should not only limit themselves to problems of the textbook, but they should also delve into advanced numerical problems, derivations and practical use of thermodynamic laws. The following table gives a comparison of the scope of NCERT vs. JEE/ NEET preparation to enable the students to prepare better.
NCERT Solutions for Class 11 Physics Chapter Wise
The NCERT Solutions for Class 11 Physics Chapter-wise links provide students with easy access to detailed, step-by-step answers for every chapter. These solutions help in building strong conceptual clarity, quick problem-solving skills, and effective exam preparation for both CBSE board exams and competitive tests like JEE and NEET.
Importance of NCERT Solutions for Class 11 Physics Chapter 11 Thermodynamics
- As the Class 11 exams and competitive exams like NEET and JEE Main are considered, the NCERT solutions for Class 11 are important.
- At least one question is expected for JEE Mains, and two questions are expected for NEET from the chapter on Thermodynamics.
NCERT Solutions for Class 11 Subject Wise
Also, check NCERT Books and NCERT Syllabus here
- NCERT Books Class 11 Physics
- NCERT Syllabus Class 11 Physics
- NCERT Books Class 11
- NCERT Syllabus Class 11
Subject-Wise NCERT Exemplar Solutions
Frequently Asked Questions (FAQs)
Q: What are some frequent thermodynamics mistakes that students should avoid?
A:
When solving problems, common mistakes include forgetting units, using thermodynamic rules incorrectly, and failing to consider assumptions. These mistakes are highlighted for self-checking by the NCERT Solutions.
Q: Why is it crucial for students in Class 11 to understand thermodynamics?
A:
It is crucial to understand thermodynamics because it establishes the foundation for more complex physics concepts as well as practical engineering and technological applications.
Q: Why is NCERT Solution Class 11 Physics important?
A:
They come in the form of step-by-step explanations to all NCERT textbook questions and thus are very useful in enabling students to comprehend the concepts properly and go into their exams well prepared.
Q: Are NCERT Solutions sufficient to prepare for JEE and NEET?
A:
Both JEE and NEET are based on NCERT, but students should also practise some reference books and solve higher-order problems to do well in the competitive exams.
Q: Is it possible to download the NCERT Solutions Class 11 Physics PDF file?
A:
Yes, NCERT Solutions are provided by us in an offline form in PDF format, chapter-wise.
Q: What are the benefits of chapter-wise solutions in exam preparation?
A:
They are prepared in such a way that they simplify revision since the concepts and questions are arranged chapter to chapter, making learning focused.
Q: Do NCERT Solutions contain major formulas?
A:
Yes, most solutions point to important formulas, and shortcuts, and they are very important in solving numerical problems in exams.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters