NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Notes for Class 11 Physics Chapter 2: Download PDF

The Motion in a Straight Line Class 11 Notes offer systematic knowledge about major concepts, equations, and examples of solved problems, and students are able to revise faster. Such notes have been prepared according to the current CBSE syllabus, hence they are very trustworthy in exam preparation. Having a downloadable PDF, the students will be able to comprehend the material at any time and read it to study effectively and perform better.

Download PDF

NCERT Notes for Class 11 Physics Chapter 2

The Motion in a Straight Line Class 11 Notes allow the students to understand this chapter in a simple and straightforward way. They describe some of the basic terms like position, displacement, velocity, acceleration, and graphs of motion in a simple manner. Class 11 Physics Motion in a Straight Line Notes are developed according to the NCERT curriculum, having brief points that enable learners to study, revise and remember important points in an easier way.

Rest and Motion

An object is said to be at rest if it remains stationary in relation to a specific frame of reference over time. On the other hand, if an object's position relative to a frame of reference changes over time, it is said to be in motion. A coordinate system to which observers attach coordinates to describe events and observations is referred to as a frame of reference.

Frame of Reference

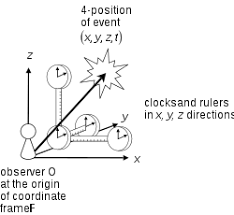
• A frame of reference is a coordinate system used to describe the position and motion of objects by providing a set of axes relative to an observer's perspective.
• According to the frame of reference:

• A body is considered in motion if its position changes over time relative to that frame, and it is considered at rest if there is no change in its position within that frame of reference. For instance, when observing a moving vehicle from an external reference frame, it appears to be in motion, while from an internal frame within the vehicle, the surroundings may seem stationary.

Motion Along a Straight Line

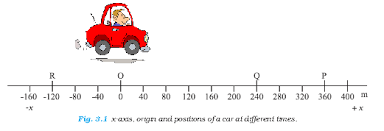
• A straight-line motion can be effectively described using only the X-axis of a coordinate system. One-dimensional motion is the movement of a body in a straight line that occurs when only one coordinate of the body's position changes with time. Examples of one-dimensional motion include the motion of a car on a straight road and the motion of a freely falling body.

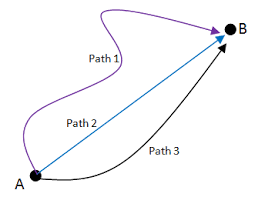
Path Length (Distance) Vs. Displacement

• Path Length: The distance between two points along a route, a scalar quantity that represents the total length travelled.
• Displacement: The change in position of a body, often denoted by ∆x = (x₂ - x₁), and it is a vector quantity indicating the overall change in position. In short, path length considers the total distance travelled, whereas displacement considers the net change in position from the initial to the final point while taking direction into account.

• The magnitude of displacement may or may not be equal to the length of the path.

• When an object returns to its original position along a path with a non-zero length, displacement can be zero. Displacement takes into account the change in position regardless of the total distance travelled, as well as the direction of motion.

Speed

• Speed is defined as the rate at which distance is covered with time. Here are some characteristics of speed:
• It is a scalar quantity denoted by the symbol v.
• Dimension: [M^oL¹T^-1]
• Unit: Meter/second (S.I.), cm/second (C.G.S.)
• Types of speed

(a) Uniform speed: A particle moves at uniform speed when it covers equal distances in equal intervals of time, regardless of how small those intervals are. For example, a car travels an equal distance of 5 metres per second, indicating a uniform speed of 5 m/s. Uniform speed denotes a constant rate of motion with no acceleration or deceleration during the time intervals specified.

(b) Non-uniform (variable) speed: A particle with non-uniform (variable) speed travels unequal distances in equal time intervals. For example, a car travels 5m in the first second, 8m in the second second, 10m in the third second, 4m in the fourth second, and so on. This variation in distance covered indicates that the particle's speed varies for each one-second interval, confirming that it moves at a variable speed. Variable speed denotes that the rate of motion varies over time.

(c) Average speed: The average speed (Vavg) of a particle for a given interval of time is defined as the ratio of the total distance travelled (d) to the total time taken (t).

${\mathrm{\$v\_\{\backslash text\; \{avg\; \}\}=\backslash frac\{\backslash text\; \{\; Distance\; traveled\; \}\}\{\backslash text\; \{\; Time\; taken\; \}\}=\backslash frac\{d\}\{t\}\$}}_{}$

(d) Instantaneous speed: It is the speed of a particle at a specific point in time. When we talk about "speed," we usually mean instantaneous speed.

$$\text{Instantaneous speed \$v=lim \_{Delta t rightarrow 0} frac{Delta s}{Delta t}=frac{d s}{d t}\$}$$

Velocity

• Velocity is defined as the rate of change of position or the rate of displacement with time.
• It is a vector quantity having the symbol v.
• Dimension of velocity: [M⁰L¹T^-1]
• Unit: Meter/second (S.I.), cm/second (C.G.S.)
• Types of Velocity

(1) Uniform velocity: The condition in which both the magnitude and direction of an object's velocity remain constant is referred to as uniform velocity. This occurs when the particle continues to move in the same straight line without changing direction. To put it another way, a particle with uniform velocity must travel at a constant speed along a straight path with no change in motion.

(2) Non-uniform velocity: Changes in the magnitude or direction of the velocity, or both, characterise non-uniform velocity. The particle's speed and/or direction of motion may change in this scenario. Non-uniform velocity indicates that the object is not moving in a straight line at a constant speed, but rather has variations in its motion over time.

(c) Average velocity: It is defined as the ratio of the body's displacement to the time it takes.

$$\text{Averagevelocity \$=frac{text { Displacement }}{text { Time taken }} ; vec{v}\_{a v}=frac{Delta vec{r}}{Delta t}\$}$$

(d) Instantaneous velocity: Instantaneous velocity is defined as the rate of change of the position vector of a particle with respect to time at a specific instant.

$$\text{Instantaneous velocity \$vec{v}=lim \_{t rightarrow 0} frac{Delta vec{r}}{Delta t}=frac{d vec{r}}{d t}\$}$$

Instantaneous Velocity and Speed

In real-life motion, the speed or velocity of an object may not remain constant throughout its journey. To understand how fast an object is moving at a particular instant of time, we define the concepts of instantaneous speed and instantaneous velocity.

Instantaneous Speed

Instantaneous speed is the speed of an object at a particular moment of time. It is the limit of average speed as the time interval approaches zero. In simpler terms, it tells us how fast an object is moving at an instant.

$\text{Instantaneous Speed \$=lim \_{Delta t rightarrow 0} frac{Delta s}{Delta t}\$}$

where $\mathrm{\$\backslash Delta\; s\$}$is the small displacement in the time interval $\mathrm{\Delta }t$.
Instantaneous speed is a scalar quantity and is always positive.

Instantaneous Velocity

Instantaneous velocity is defined as the velocity of an object at a particular instant of time. Like instantaneous speed, it is obtained by taking the limit of the average velocity as the time interval tends to zero.

$\stackrel{}{\mathrm{\$\backslash vec\{v\}=\backslash lim\; \_\{\backslash Delta\; t\; \backslash rightarrow\; 0\}\; \backslash frac\{\backslash Delta\; \backslash vec\{x\}\}\{\backslash Delta\; t\}=\backslash frac\{d\; \backslash vec\{x\}\}\{d\; t\}\$}}$

where $\stackrel{}{\$\backslash vec\{x\}\$}$
is the displacement vector and $t$ is time.
Instantaneous velocity is a vector quantity and has both magnitude and direction.

Acceleration

• Acceleration is defined as the time rate at which an object's velocity changes. it tells us how quickly and in which direction an object's velocity is changing. It is expressed in acceleration units such as metres per second squared.
• It is a vector quantity with the same direction as the change in velocity (not the velocity itself).
• Dimension of acceleration: $\$\backslash left[\backslash mathrm\{M\}^0\; \backslash mathrm\{~L\}^1\; \backslash mathrm\{~T\}^\{-2\}\backslash right]\$$
• Units: $\left[\right.$ meter $(\mathrm{m}) /$ second $\left.2\left(\mathrm{~s}^2\right)\right]$ in (S.I.), $\left[\right.$ centimeter $(\mathrm{cm}) /$ second $\left.2\left(\mathrm{~s}^2\right)\right]$ in (C.G.S.).
• Types of Acceleration

(a) Uniform acceleration: Uniform acceleration refers to a situation in which both the magnitude and direction of the acceleration of a body remain constant during its motion.

(b) Non-uniform acceleration: A body is said to have non-uniform acceleration if there are changes in either the magnitude or direction of acceleration, or both, during its motion.

(c) Average acceleration: The average acceleration of an object is defined as the change in velocity per unit time.

${\stackrel{}{\mathrm{\$\backslash vec\{a\}\_\{a\; v\}=\backslash frac\{\backslash Delta\; \backslash vec\{v\}\}\{\backslash Delta\; \backslash vec\{t\}\}=\backslash frac\{\backslash vec\{v\}\_2-\backslash vec\{v\}\_1\}\{\backslash Delta\; t\}\$}}}_{}$

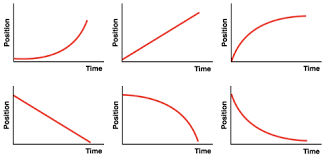
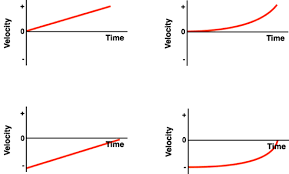
Position-Time, Velocity-Time, and Acceleration-Time Graph

p-t graph

v-t graph

Kinematic Equations for Uniformly Accelerated Motion

Using the velocity-time graph of the object under uniformly accelerated motion, we can derive a simple set of equations that relate displacement $(x)$, time $(t)$, initial velocity $(u)$, final velocity $(v)$ and acceleration (a). Let's discuss the above velocity-time graph of the object in detail. The velocity of the object changes from $u$ to $v$ in time $t$.

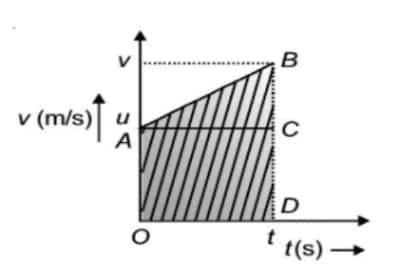
1. Derivation of the velocity-time relation

The slope of the graph gives the acceleration a of the object.

$\begin{aligned} & & a & =\frac{B C}{A C}=\frac{v-u}{t} \\ \Rightarrow & & a t & =v-u \\ \Rightarrow & & v & =u+a t----(i)\end{aligned}$$$\begin{array}{r}\end{array}$$
2. Derivation of displacement-time relation

The area under this curve is
Area of $\triangle A B C+$ area of rectangle $O A C D$
Area of $\triangle A B C=\frac{1}{2} \times(v-u) t$
Area of rectangle $O A C D=\mathrm{ut}$
And as explained in the previous section, the area under $v-t$ curve represents the displacement. Therefore, the displacement $s$ of the object is

$
s=\frac{1}{2}(v-u) t+u t-\cdots-(\mathrm{ii})
$

But $(v-u)=a t$ [from equation (i)]
Substituting this value in the above equation, we get

$
\text { or } s=u t+\frac{1}{2} a t^2
$

3. Derivation of the velocity-displacement relation

Now, the area of trapezium $O A B D=\frac{1}{2}$ (sum of parallel sides) $\times$ perpendicular distance between the parallel sides.

$
\begin{gathered}
S=\frac{1}{2} \times(O A+B D) \times O D \\
S=\frac{1}{2}(u+v) \times t
\end{gathered}
$

From equation (i), we get

$
t=\frac{v-u}{a}
$

Substituting this value of $t$ in the equation, we get

$
\begin{array}{cc}
s=\frac{1}{2}(u+v) \times \frac{(v-u)}{a} \\
\Rightarrow s=\frac{v^2-u^2}{2 a} \\
\Rightarrow v^2-u^2=2 a s
\end{array}
$

$s$ is the displacement of the object in the time interval $t$ and is given by the change in the position from $x_0$ to $x$

$
s=\left(x-x_0\right)
$

So the three kinematic equations of uniformly accelerated motion that we have derived so far are

$
\begin{aligned}
v & =u+a t \\
x-x_0 & =u t+\frac{1}{2} a t^2 \\
v^2-u^2 & =2 a\left(x-x_0\right)
\end{aligned}
$

$\begin{array}{r}\end{array}$

Relative Velocity

The relative velocity of an object $A$ with respect to another object $B$ is the velocity with which $A$ appears to move when seen from $B$.

if
$\vec{v}_A$ is the velocity of object A, and
$\vec{v}_B$ is the velocity of object B, then the relative velocity of $A$ with respect to $B$ is given by:

$
\vec{v}_{A B}=\vec{v}_A-\vec{v}_B
$

Similarly, the relative velocity of $B$ with respect to $A$ is:

$
\vec{v}_{B A}=\vec{v}_B-\vec{v}_A=-\vec{v}_{A B}
$${}_{}$

Class 11 Physics Chapter 2 Motion in a Straight Line: Previous Year Question and Answer

Q1: A ball is bouncing elastically with a speed of 1 m/s between the walls of a railway compartment of size 10 m in a direction perpendicular to the walls. The train is moving at a constant velocity of 10 m/s parallel to the direction of motion of the ball. As seen from the ground,

a) The direction of motion of the ball changes every 10 seconds

b) The speed of the ball changes every 10 seconds

c) The average speed of the ball over any 20-second intervals is fixed

d) the acceleration of the ball is the same as that of the train

Answer:

The correct answers are:

(b) The speed of the ball changes every 10 seconds.
(c) The average speed of the ball over any 20-second interval is fixed.
(d) The acceleration of the ball is the same as that of the train.

Explanation: If we observe the motion from the ground, we will see that the ball strikes the wall every 10 seconds. The direction of the ball is the same since it is moving at a very small speed in the moving train; therefore, it will not change w.r.t. observer to the Earth.

The speed of the ball can change after a collision; hence, statement (a) will be discarded and statement (b) will be verified.
The average speed of the ball at any time remains the same or is $1 \mathrm{~m} / \mathrm{s}$, i.e., it is uniform.
Hence, statement (c) is also verified.
When the ball strikes the wall, the initial speed of the ball will be in the direction of the moving train w.r.t. the ground as well, and its speed will also change (vTG)

Thus, $V_{T G}=10+1=11 \mathrm{~m} / \mathrm{s}$
The speed of the ball after collision with a side of the train is in the opposite direction to the train.

$
\left(v_{B G}\right)=10-1=9 \mathrm{~m} / \mathrm{s}
$
Thus, the magnitude of acceleration on both the walls of the compartment will be the same, but in opposite directions. Hence, statements (b), (c) & (d) are verified here.

Q2:

The variation of quantity A with quantity B, plotted in Fig. 3.2 describes the motion of a particle in a straight line.

(a) Quantity B may represent time.
(b) Quantity A is velocity if motion is uniform.
(c) Quantity A is displacement if motion is uniform.
(d) Quantity A is velocity if motion is uniformly accelerated.

Answer:

The correct answers are:

(a) Quantity B may represent time.

(c) Quantity A is displacement if the motion is uniform.

(d) Quantity A is velocity if the motion is uniformly accelerated.

Explanation:

Verification of statements (a) & (d)

If quantity B had represented velocity instead of time, then the graph would’ve become a straight line, viz., uniformly accelerated motion, hence the motion is not uniform.

Verification of statement (c)

If A represents displacement and B represents time, then the graph will be a straight line, which would represent uniform motion.

Q3:

The displacement of a particle is given by $x=(t-2)^2$ where x is in metres and t is in seconds. The distance covered by the particle in the first 4 seconds is

(a) 4 m

(b) 8 m

(c) 12 m

(d) 16 m

Answer:

Explanation: It is given that $x=(t-2)^2$
Now, we know that,

$
\begin{aligned}
V & =\frac{d x}{d t} \\
& =2(t-2) \mathrm{m} / \mathrm{s}
\end{aligned}
$

$
\begin{aligned}
a= & \frac{d^2 x}{d t^2} \\
& =2(1-0) \\
& =2 \mathrm{~ms}^{-2}
\end{aligned}
$

Now,

$
\begin{array}{ll}
v_0=2(0-2)=-4 m / \mathrm{s} & \ldots \ldots \ldots \ldots(\text { at } t=0) \\
v_2=2(2-2)=0 \mathrm{~m} / \mathrm{s} & \ldots \ldots \ldots \ldots(\text { at } t=2) \\
v_4=2(4-2)=4 \mathrm{~m} / \mathrm{s} & \ldots \ldots \ldots \ldots(\text { at } t=4)
\end{array}
$

$\begin{aligned} & =\frac{1}{2}(2.4)+\frac{1}{2}(2.4) \\ & =8 \mathrm{~m}\end{aligned}$

Hence, the correct answer is option (b).

Importance of Motion in a Straight Line Class 11 Notes

The Motion in a Straight Line Class 11 Notes are significant because they form the basis of the field of physics known as kinematics. Complex concepts such as displacement, velocity and acceleration are made easier to learn and use using these notes. They are well explained and comprise formulas and examples, and can thus be used to revise quickly when necessary during examination time and to prepare for competitive exams such as JEE and NEET.

Strong Foundation for Higher Studies

• Motion in a straight line Class 11 Notes assists the student to develop a clear picture of kinematics in a one-dimensional system, which is a prerequisite to higher-order ideas in mechanics, rotational motion and dynamics.

Time-Saving Revision Material

• Properly organised NCERT Class 11 Physics Chapter 2 Notes enable students to memorise all formulas, graphs and derivations within a short period of time before examinations and thus save a lot of time.

Enhances Problem-Solving Abilities

• The notes contain conceptual excellence on displacement, velocity, acceleration, and motion graphs, and this enhances the precision in solving problems in CBSE exams, JEE, and NEET.

Includes All Significant Formulas

• Students receive a brief list of equations of motion, graphical relations and derivations, and they do not need to skip important formulae in last-minute revision.

Exam-Oriented Preparation

• NCERT Class 11 Physics Chapter 2 Notes pinpoint key points and past exam directions so that one can concentrate on areas that will score more marks.

Helps Competitive Exam Aspirants

• Linear motion is a very important chapter for JEE Mains, JEE Advanced and NEET Physics. These notes make complicated ideas easier and the practice more effective.

Improves Conceptual Learning

• The Motion in a straight line Class 11 Notes describe the practical examples of a motion (such as a car that moves on a straight road), and the students can connect theory to the real-life examples.

How to Use NCERT Class 11 Physics Chapter 2 Notes Effectively?

Using the NCERT Class 11 Physics Chapter 2 – Motion in a Straight Line Notes effectively can make learning easier and faster. With clear explanations, solved examples, and key formulas, these notes are designed to help students grasp concepts quickly, practice problems efficiently, and revise topics confidently for exams and competitive tests.

• Start with Concepts: Begin by reading the short, clear explanations to understand key concepts like displacement, velocity, acceleration, and relative motion.
• Learn Formulas: Note down all important formulas separately and understand their derivation and applications.
• Solve Examples: Practice the solved examples in the notes to see how theory is applied in problems.
• Revise Graphs: Pay special attention to position-time and velocity-time graphs, as they are frequently asked in exams.
• Self-Assessment: After studying, attempt unsolved numerical problems from the textbook or previous year questions to reinforce understanding.
• Regular Revision: Use the notes for quick daily revisions before exams for better retention.

NCERT Class 11 Notes Chapter-Wise

NCERT Class 11 Notes Chapter-wise provide concise, well-structured summaries of all Physics chapters as per the latest CBSE syllabus. These notes help students grasp key concepts, formulas, and derivations quickly, making them ideal for board exams and competitive exams like JEE and NEET. With chapter-wise links, you can easily navigate and revise topics in an organised way.

Subject-Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus